Segment Tree를 활용한 2D Range Update/Query
이 포스트는 Nabil Ibtehaz, Mohammad Kaykobad, Mohammad Sohel Rahman의 Multidimensional segment trees can do range queries and updates in logarithmic time 논문에서 핵심 아이디어를 가져와 작성한 것입니다.
독자가 1/2차원 세그먼트 트리와 Lazy propagation에 대한 지식을 알고 있다고 가정하고 글을 작성합니다. 아래에 제시된 코드는 모두 Kotlin으로 작성하였습니다.
목표
이 글의 목표는 2차원 세그먼트 트리를 이용해 $n \times m$ 크기의 2차원 배열 $A$에 다음과 같은 연산을 $O(\log n \log m)$ 시간에 수행하는 것입니다.
- Update: 모든 $(x, y) \in [x_1, x_2) \times [y_1, y_2)$와 주어진 값 $c$에 대해 $A[x][y] \leftarrow A[x][y] + c$
- Query: $\sum_{(x, y) \in [x_1, x_2) \times [y_1, y_2)} A[x][y]$ 구하기
실제로는 교환법칙과 결합법칙이 성립하는 모든 연산자(곱셈, xor, and, or, min, max 등)에 대해서도 Update와 Query를 수행할 수 있습니다.
2차원 세그먼트 트리의 구조
일반적인 방법과 같이, 1차원 세그먼트 트리의 각 노드에 1차원 세그먼트 트리를 저장하는 방식을 사용합니다. 첫 번째 차원을 $x$축, 두 번째 차원을 $y$축이라고 하겠습니다.
먼저, $x$축을 기준으로 하는 1차원 세그먼트 트리의 구조를 잡습니다.
이 트리의 각 노드에는 $y$축에 대한 1차원 세그먼트 트리의 루트 yRoot와
자신의 자식 노드 left, right만 저장합니다.
이 노드가 담당하고 있는 $x$축의 구간은 Update 및 Query 과정에서 구할 수 있으므로
메모리 절약을 위해 따로 저장하지 않습니다.
data class xNode(
val yRoot : yNode? = null,
var left : xNode? = null,
var right: xNode? = null
)
다음으로, $y$축을 기준으로 하는 1차원 세그먼트 트리의 구조를 잡습니다.
이 트리의 각 노드에는 질의를 처리하는 데에 필요한 정보를 담은
globalRowSum, globalRowLazy, totalSum, totalLazy와,
자신의 자식 노드 left, right를 저장하며,
이 노드가 담당하는 구간은 xNode와 같은 이유로 저장하지 않습니다.
각 변수의 의미는 다음 섹션에서 다룹니다.
data class yNode(
var globalRowSum: Value = Value(),
var globalRowLazy: Value = Value(),
var totalSum: Value = Value(),
var totalLazy: Value = Value(),
var left: yNode? = null,
var right: yNode? = null
)
Update
예시를 들며 설명해 보겠습니다. $H = 7$일 때, $x$축 세그먼트 트리는 아래와 같이 구축할 수 있습니다.
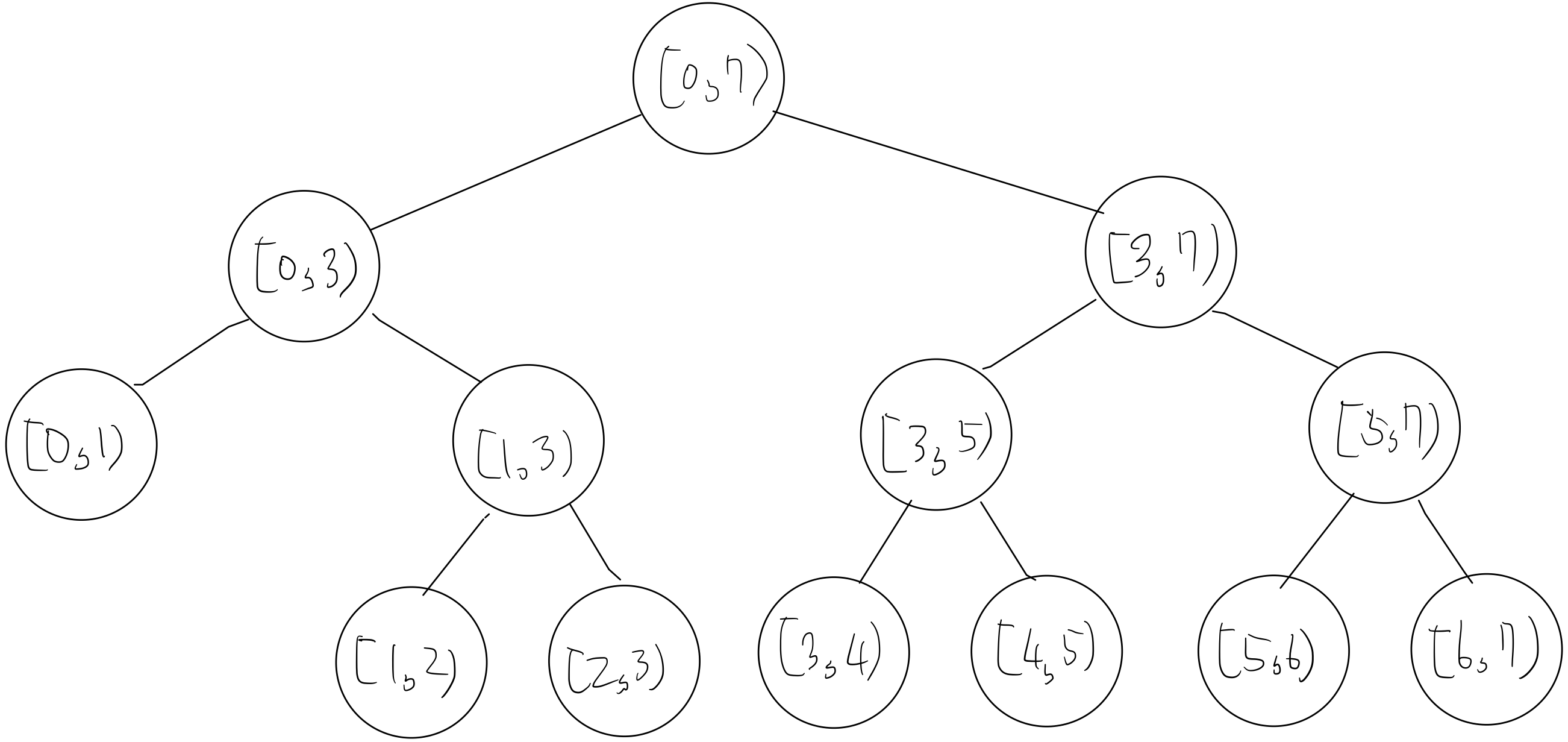
이 상태에서, 어떤 $x$축 구간 $[x_1, x_2)$를 업데이트하려고 한다고 합시다. 루트에서 아래로 내려가면서, 노드가 덮고 있는 구간이 $[x_1, x_2)$에 완전히 포함되면 노란색, 노란색 노드에 닿기 위해 방문해야 할 조상 노드들을 푸른색으로 색칠합니다. 아래 그림은 $[2, 6)$ 구간에 대해 각 노드를 색칠한 결과입니다. 이제 색에 따라 다른 방식으로 각 노드에 저장된 $y$축 세그먼트 트리를 업데이트해야 합니다.

노란색 노드 업데이트하기
노란색 노드가 덮고 있는 $x$축 반개구간을 $[nx_1, nx_2)$라고 합시다. $[nx_1, nx_2)$가 $[x_1, x_2)$에 완전히 포함되어 있기 때문에, 배열 $A$의 모든 행(줄)의 똑같은 $y$축 위치에 똑같은 값이 더해지게 된다고 생각할 수 있습니다.

따라서, 이 경우에는 노란색 노드가 갖고 있는 $y$축 세그먼트 트리가
$nx_1$번 행(아무 행이나 잡아도 됨)의 정보를 관리하도록 하면 충분합니다.
그러면 업데이트는 1차원 세그먼트 트리에서 $[y_1, y_2)$ 구간에 $c$를 더하는 것과 같으므로,
전형적인 Lazy propagation 방식을 그대로 이용하면 됩니다.
여기에 사용되는 변수가 globalRowSum과 globalRowLazy입니다.
이 과정은 lazy propagation을 활용한 1차원 구간 업데이트 알고리즘에서 lazy tag에 $c$를 더하는 것에 비유할 수 있습니다.
푸른색 노드 (및 노란색 노드) 업데이트하기
다시 1차원 구간 업데이트 알고리즘을 생각해 보면, 노란색 노드를 처리하고 난 뒤 루트로 돌아오면서 각 노드에 저장된 부분합을 관리해 주었죠. 노란색 노드의 경우 합에 $c \times $ (구간 길이)를 더했고, 푸른색 노드의 경우 두 자식 노드에 저장된 두 부분합을 합쳤습니다.
2차원에서도 비슷한 느낌으로 각 $x$축 세그먼트 트리의 노드가 어떤 부분합을 가지고 있어야 할 것입니다. 따라서, 푸른색 노드가 담당하고 있는 모든 행벡터의 합을 $y$축 세그먼트 트리에서 관리합니다.
다른 방식으로 표현하자면, $y$축 세그먼트 트리의 한 노드가 담당하고 있는 구간이 $[nx_1, nx_2) \times [ny_1, ny_2)$일 때, 이 노드는 대략 $\sum_{(x, y) \in [nx_1, nx_2) \times [ny_1, ny_2)} A[x][y]$의 값을 관리한다고 생각할 수 있습니다. (정확한 표현은 아닙니다. ‘주의할 점’ 부분 참고)
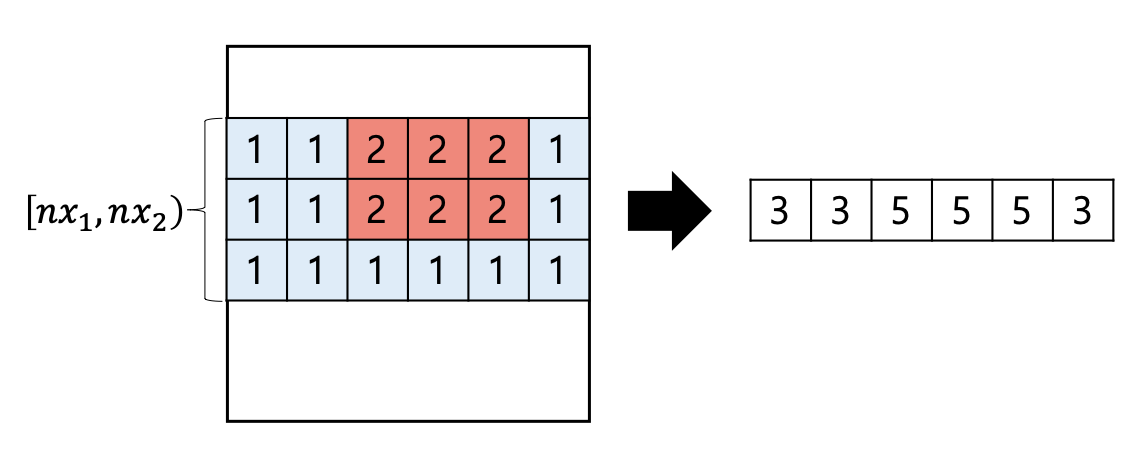
그러면 업데이트는 1차원 세그먼트 트리에서 $[y_1, y_2)$ 구간에
$c \times |[x_1, x_2) \cap [nx_1, nx_2)|$를 더하는 것과 같으므로,
역시 전형적인 Lazy propagation 방식을 그대로 이용하면 됩니다.
여기에 이용되는 변수가 totalSum과 totalLazy입니다.
주의할 점은, 1차원 구간 업데이트 알고리즘과는 달리
2차원에서는 $x$축 세그먼트 트리의 자식 노드로 lazy tag에 해당하는 global 값들을 전달할 수가 없기 때문에,
여기서 저장되는 값들에는 $x$축 세그먼트 트리에서 조상 노드가 노란색이었을 때 한 업데이트들이 누락되어 있다는 것입니다.
코드
fun update(x1: Int, x2: Int, y1: Int, y2: Int, c: Value) {
// [x1, x2) x [y1, y2) 범위에 c를 더하는 함수
fun updateX(xnd: xNode, nx1: Int, nx2: Int, ux1: Int, ux2: Int) {
// x축 세그먼트 트리를 순회하며, 각 노드의 y축 세그먼트 트리를 업데이트하도록 하는 함수
// 현재 노드가 xnd이며, 이 노드는 [nx1, nx2) 구간을 담당함.
// 업데이트할 범위는 [ux1, ux2)이며, 이는 노드가 담당하는 범위에 완전히 포함됨.
if(nx1 != ux1 || nx2 != ux2) {
// xnd가 푸른색 노드이므로, 더 아래로 내려가야 함
val nxm = (nx1 + nx2) / 2
if(ux1 < nxm) {
if(xnd.left == null) xnd.left = xNode()
updateX(xnd.left!!, nx1, nxm, ux1, minOf(ux2, nxm))
}
if(nxm < ux2) {
if(xnd.right == null) xnd.right = xNode()
updateX(xnd.right!!, nxm, nx2, maxOf(nxm, ux1), ux2)
}
}
fun updateY(ynd: yNode, ny1: Int, ny2: Int, uy1: Int, uy2: Int) {
// y축 세그먼트 트리에서 lazy propagation으로 구간 업데이트하는 함수
// 현재 노드가 ynd이며, 이 노드는 [nx1, nx2) x [ny1, ny2) 구간을 담당함.
// 업데이트할 범위는 [ux1, ux2) x [uy1, uy2)이며, 이는 노드가 담당하는 범위에 완전히 포함됨.
if(ny1 == uy1 && ny2 == uy2) {
if(nx1 == ux1 && nx2 == ux2) { // xnd가 노란색 노드이므로, global 값들을 업데이트함
ynd.globalRowSum += c * (uy2 - uy1)
ynd.globalRowLazy += c
}
ynd.totalSum += c * (ux2 - ux1) * (ny2 - ny1)
ynd.totalLazy += c * (ux2 - ux1)
}else {
val nym = (ny1 + ny2) / 2
if(uy1 < nym) {
if(ynd.left == null) ynd.left = yNode()
updateY(ynd.left!!, ny1, nym, uy1, minOf(uy2, nym))
}
if(nym < uy2) {
if(ynd.right == null) ynd.right = yNode()
updateY(ynd.right!!, nym, ny2, maxOf(uy1, nym), uy2)
}
if(nx1 == ux1 && nx2 == ux2) {
ynd.globalRowSum = (ynd.left ?.globalRowSum ?: Value()) +
(ynd.right ?.globalRowSum ?: Value()) +
ynd.globalRowLazy * (ny2 - ny1)
}
ynd.totalSum = (ynd.left ?.totalSum ?: Value()) +
(ynd.right ?.totalSum ?: Value()) +
ynd.totalLazy * (ny2 - ny1)
}
}
// y축 세그먼트 트리의 [y1, y2) 범위를 업데이트함
updateY(xnd.yRoot, 0, cols, y1, y2)
}
updateX(root, 0, rows, x1, x2)
}
Query
Update에서 사용한 예시를 가져오겠습니다.
똑같은 방식으로 $x$축 세그먼트 트리의 각 노드를 노란색과 푸른색으로 색칠할 수 있습니다.
노란색 노드와 푸른색 노드에서 서로 다른 방식으로 답을 구해야 합니다.
답을 저장하는 변수를 ret이라 하겠습니다.

노란색 노드
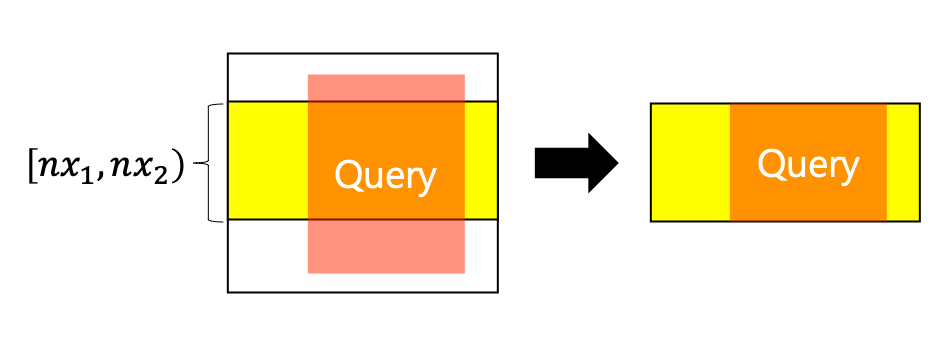
노란색 노드가 나왔으므로, $x$축 세그먼트 트리를 탐색하는 과정에서 더 아래로 내려가지는 않을 것입니다.
그리고, 이 노란색 노드의 totalSum들에는 노란색 노드가 담당하는 $x$축 구간 내에서 일어난
모든 업데이트 결과가 반영되어 있습니다.
이 사실을 기억해 둔 채로
$y$축 세그먼트 트리의 $[y_1, y_2)$ 구간에서 total 부분의 합을 구해서 ret에 더해 놓습니다.
이것 역시 전형적인 Lazy Propagation 방식을 그대로 이용하면 됩니다.
푸른색 노드
노란색 노드의 total 값들을 다 합쳤다고 합시다.
이제 처리해야 할 부분은, 현재의 푸른색 노드가 Update 과정에서 노란색이었을 때 한 global 업데이트가
주어진 범위 $[x_1, x_2) \times [y_1, y_2)]$에 미친 영향을 구하는 것입니다.
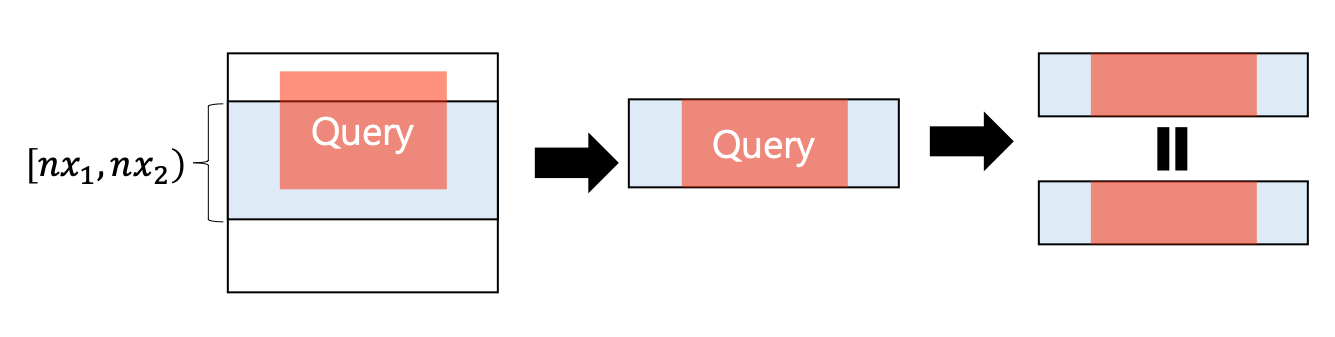
그런데, global 업데이트는 모든 행의 똑같은 열에 똑같은 값을 더하므로,
각 행마다 추가적으로 더해줘야 하는 합 또한 서로 같을 것입니다.
따라서, $y$축 세그먼트 트리의 $[y_1, y_2)$ 구간에서 global 부분의 합을 구한 뒤,
겹치는 행 개수인 $|[x_1, x_2) \cap [nx_1, nx_2)|$를 곱해서 ret에 더해 주면 됩니다.
코드
fun query(x1: Int, x2: Int, y1: Int, y2: Int): Value {
// [x1, x2) x [y1, y2) 범위의 합을 구하는 함수
var ret = Value()
fun queryX(xnd: xNode, nx1: Int, nx2: Int, qx1: Int, qx2: Int) {
// x축 세그먼트 트리를 순회하며, 각 노드의 y축 세그먼트 트리에 저장된 값들을 적절히 가져오도록 하는 함수
// 현재 노드가 xnd이며, 이 노드는 [nx1, nx2) 구간을 담당함.
// query의 x축 범위는 [ux1, ux2)이며, 이 범위는 노드가 담당하는 범위에 완전히 포함됨.
if(nx1 != qx1 || nx2 != qx2) {
val nxm = (nx1 + nx2) / 2
if(qx1 < nxm && xnd.left != null) {
queryX(xnd.left!!, nx1, nxm, qx1, minOf(qx2, nxm))
}
if(nxm < qx2 && xnd.right != null) {
queryX(xnd.right!!, nxm, nx2, maxOf(nxm, qx1), qx2)
}
}
fun queryY(ynd: yNode?, ny1: Int, ny2: Int, qy1: Int, qy2: Int, tag: Value) {
// y축 세그먼트 트리에서 lazy propagation으로 구간의 합을 구하는 함수.
// 현재 노드가 ynd이며, 이 노드는 [nx1, nx2) x [ny1, ny2) 구간을 담당함.
// query 범위는 [ux1, ux2) x [uy1, uy2)이며, 이는 노드가 담당하는 범위에 완전히 포함됨.
// 주의: 이 함수만 ynd가 Nullable인데,
// 세그먼트 트리가 동적으로 생성되기 때문에 lazy tag를 자식 노드로 push할 수 없어서
// 조상에서부터 구한 lazy들의 합을 `tag`에 저장했기 때문임.
// ynd가 null이라면 아직 생성되지 않은 가상의 노드에서 합을 구하고 있다고 생각하면 됨.
if(ny1 == qy1 && ny2 == qy2) {
if(nx1 == qx1 && nx2 == qx2) { // ndx가 노란색 -> total
if(ynd != null) ret += ynd.totalSum
ret += tag * (ny2 - ny1)
}else { // ndx가 푸른색 -> global 값
if(ynd != null) ret += ynd.globalRowSum * (qx2 - qx1)
ret += tag * (qx2 - qx1) * (ny2 - ny1)
}
}else {
val next_tag = when {
ynd == null -> tag
nx1 == qx1 && nx2 == qx2 -> tag + ynd.totalLazy // ndx가 노란색
else -> tag + ynd.globalRowLazy // ndx가 푸른색
}
val nym = (ny1 + ny2) / 2
if(qy1 < nym) {
queryY(ynd?.left, ny1, nym, qy1, minOf(qy2, nym), next_tag)
}
if(nym < qy2) {
queryY(ynd?.right, nym, ny2, maxOf(qy1, nym), qy2, next_tag)
}
}
}
queryY(xnd.yRoot, 0, cols, y1, y2, Value())
}
queryX(root, 0, rows, x1, x2)
return ret
}
사용 예시
덧셈 연산을 적용하고 싶다면 아래와 같이 Value 클래스를 만들면 됩니다.
times 함수는 연산의 기본 값(보통 항등원)에 plus 연산을 other번 적용했을 때의 결과를 반환하도록 해야 합니다.
data class Value(val v: Long = 0) {
override fun toString() = "$v"
constructor(v: Int): this(v.toLong())
operator fun plus(other: Value) = Value(v + other.v)
operator fun times(other: Int) = Value(v * other)
operator fun times(other: Long) = Value(v * other)
}
예를 들어, xor 연산을 적용하고 싶다고 합시다.
xor의 항등원 0에 v를 other번 적용한 결과는, other가 짝수라면 0이고 홀수라면 v입니다.
따라서 Value 클래스를 아래와 같이 작성할 수 있습니다.
data class Value(val v: Long = 0) {
override fun toString() = "$v"
constructor(v: Int): this(v.toLong())
operator fun plus(other: Value) = Value(v xor other.v)
operator fun times(other: Int) = Value(v * (other % 2))
operator fun times(other: Long) = Value(v * (other % 2))
}
min 연산도 비슷하게 작성할 수 있습니다.
data class Value(val v: Long = Long.MAX_VALUE) {
override fun toString() = "$v"
constructor(v: Int): this(v.toLong())
operator fun plus(other: Value) = Value(minOf(v, other.v))
operator fun times(other: Int) = Value(v)
operator fun times(other: Long) = Value(v)
}
시간복잡도 및 공간복잡도 분석
$x$축 세그먼트 트리에서 $O(\log n)$개의 노드를 방문하고, 각 $x$축 노드마다 $y$축 세그먼트 트리에서 $O(\log m)$개의 노드를 방문하므로 시간복잡도는 총 $O(\log n \log m)$입니다. 단, 이는 Value의 덧셈과 곱셈을 하는 데에 드는 시간이 $O(1)$이라고 가정하고 측정한 것입니다.
공간복잡도는, 한 번의 업데이트가 있을 때마다 최대 $O(\log n \log m)$개의 노드가 생성되므로 $O(Q \log n \log m)$입니다. 또한, 업데이트가 많다면 정적으로 $2n \times 2m$ 크기의 배열을 잡아놓는 것이 시간상 유리할 수 있습니다.