January 3, 2019 15:00

목표

LiChao Tree는 직선이 실시간으로 추가되는 Convex hull trick 문제를 해결하기 위한 자료구조입니다. 구현이 비교적 간단하면서 유용한 자료구조인데, 한글로 설명된 자료가 없어 포스트를 작성하게 되었습니다.

이 포스트의 목표는 LiChao Tree를 이용해 (백준 12795) 반평면 땅따먹기 문제를 해결하는 것입니다. 이 문제를 해결하는 방법은 다양하지만, LiChao Tree를 사용한 솔루션이 가장 수행시간이 빠릅니다.

사전지식 - Dynamic Segment Tree

LiChao Tree는 Dynamic Segment Tree에 기반한 자료구조입니다. Dynamic Segment Tree란 구간의 범위에 따라 모든 노드를 만들어놓고 시작하는 일반적인 Segment Tree와는 달리 쿼리가 들어올 때마다 그때그때 필요한 노드를 생성해나가는 Segment Tree 입니다.

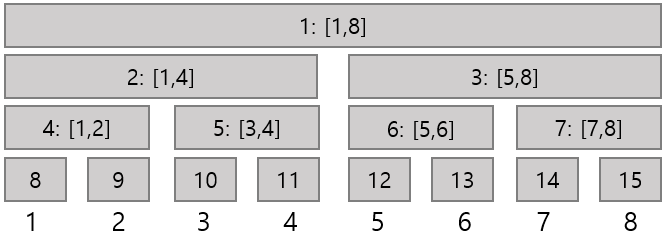
이해를 돕기 위해 예시를 들어보겠습니다. Range increment update / Point value query 연산을 수행하는 일반적인 Segment Tree를 생각합시다. index 범위가 $ 1…8 $ 이라면 아래 그림과 같이 15개의 노드가 만들어진 상태로 시작할 것입니다. 이후 각 연산마다 $ O(lg8) $ 개의 노드를 살펴보면서 쿼리들을 처리할 수 있을 것입니다.

그러나 Dynamic Segment Tree는 전체 구간을 관리하는 루트 노드 하나만 만들어진 채로 시작합니다.

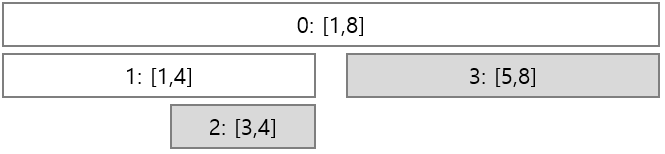
여기서 $ [3,8] $ 구간에 1을 더하는 연산을 수행하려면 어떻게 해야 할까요? 필요한 노드들을 생성해서 자식으로 붙여 주면 됩니다. 아래 그림과 같이 트리가 확장될 것입니다. 확장과 동시에 회색 노드들의 값을 갱신해주면 됩니다.

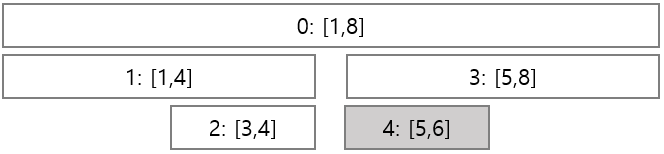
이후에 $ [5,6] $ 구간에 1을 더하는 연산이 들어오면 아래 그림과 같이 트리가 확장될 것입니다. 마찬가지로 확장과 동시에 회색 노드의 값을 갱신해주면 됩니다.

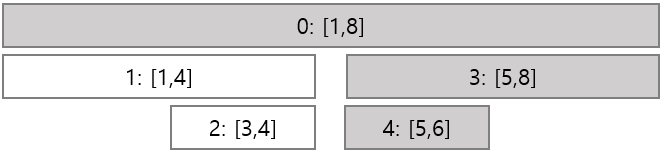
이제 $ x=5 $ 위치의 값을 구하려는 상황을 생각해 봅시다. 기존의 일반적인 Segment Tree에서는 담당하는 구간이 $ x=5 $를 포함하는 모든 노드를 확인했습니다. Dynamic Segment Tree의 경우에도 마찬가지이지만, 생성되지 않은 노드에 대해서는 걱정할 필요가 없으므로 존재하는 노드들 중에 담당하는 구간이 $ x=5 $ 를 포함하는 노드들만 확인하면 될 것입니다. 확인해야 될 노드들을 표시해 보면 아래 그림과 같습니다.

이러한 Dynamic Segment Tree의 시간복잡도는 일반적인 Segment Tree와 마찬가지로 연산당 $ O(lgX) $입니다. 한번의 연산을 수행할 때 확인해야 할 노드(생성되는 것 포함)들의 개수가 최대 $ O(lgX) $ 개라는 점에서 쉽게 확인할 수 있습니다.

시간복잡도가 같은데 일반적인 Segment Tree 보다 무슨 장점이 있는 걸까요? 바로 구간의 길이인 $ X $ 의 범위에 제한이 없다는 것입니다. 일반적인 Segment Tree에서는 처음에 $ O(X) $ 개의 노드를 미리 만들어 놓고 시작합니다. 그러나 $ X $ 가 너무 큰 경우 좌표압축 등의 테크닉이 추가로 필요하거나, Segment Tree 활용 자체가 아예 불가능할 수도 있습니다. 그러나 Dynamic Segment Tree의 경우 쿼리 한번당 최대 $ O(lgX) $ 개의 노드가 추가로 생성됩니다. 따라서 최종적으로 만들어지는 노드의 총 개수가 $ O(QlgX) $ 개이므로 $ X $가 매우 큰 수여도 활용이 가능합니다.

이후 LiChao Tree코드를 작성할 때 자연스럽게 Dynamic Segment Tree 구현이 등장하므로 따로 코드는 작성하지 않고 진행하겠습니다.

문제 소개

이제 본격적으로 LiChao Tree에 대한 내용을 알아봅시다. 먼저, 다음과 같은 두 쿼리를 처리해야 하는 문제를 생각합시다. (반평면 땅따먹기 문제의 쿼리와 동일합니다.)

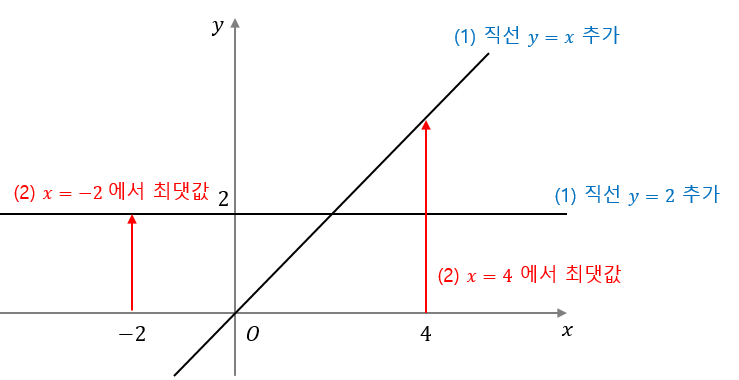
(1) 직선 $ y=ax+b $ 를 집합에 추가

(2) 집합에 존재하는 직선들 중, 주어진 $ x=x_i $ 위치에서의 최댓값을 출력

이 형태가 (삭제 연산이 없는) 일반적인 Convex hull trick 문제입니다. 대부분의 Convex hull trick 문제는 결국 위 두 연산을 빠르게 수행할 수 있다면 풀 수 있는 문제로 변환됩니다.

우리의 목표는 각 쿼리를 $ O(lgX) $ 에 수행하므로써 최종적으로 문제를 $ O(QlgX) $ 시간복잡도에 해결하는 것입니다. 여기서 $ Q $ 는 쿼리의 총 개수, $ X $ 는 문제에서 주어진 $ x $ 좌표 범위의 길이입니다.

LiChao Tree

LiChao Tree는 Dynamic Segment tree의 일종입니다. 각 노드는 특정 $ x $ 구간에서 가장 위에 있는 (최댓값을 가지는) 직선 하나씩을 저장하고 있게 됩니다.

LiChao Tree는 여느 Segment tree와 비슷하게 insert와 get함수를 가집니다. 이름에서 예상할 수 있듯이, insert함수는 집합에 직선을 추가하는 함수이고, get함수는 특정 $ x=x_q $ 좌표에서 대해 집합에 있는 직선들 중 최댓값을 반환하는 함수입니다.

(1) 직선 추가 쿼리 (insert)

void insert(int n, Line newline)

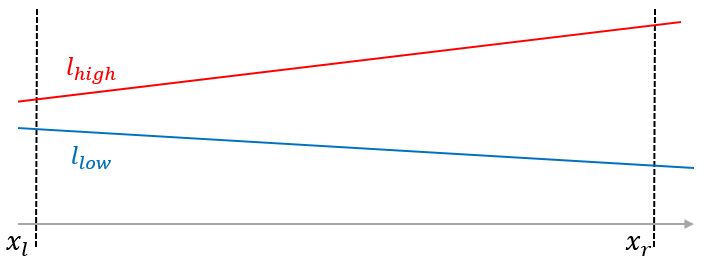
insert 함수는 특정 노드가 담당하는 구간 $ x=[x_l…x_r] $ 에 새로운 직선을 추가하는 함수입니다. 이 함수가 호출되면, $ n $번 노드는 기존에 저장하고 있던 직선과 비교해서 더 유리한 직선(위에 있는 직선) 하나를 선택해 새로 저장하게 될 것입니다. 먼저, 구간의 왼쪽 끝을 기준으로 $ l_{low} $ 와 $ l_{high} $ 를 결정합시다.

아래 그림과 같이 구간 내에서 한 직선이 항상 다른 직선보다 위에 있는 경우는 어떤 것을 선택해야 할지 명확합니다.

그런데 두 직선이 교차하는 경우는 어떤 것이 더 유리한지가 명확하지 않습니다. 이 경우는 두 직선의 교점이 구간의 중점 $ x_m = (x_l+x_r)/2 $ 기준으로 어느 쪽에 있는지에 따라 달라지게 됩니다.

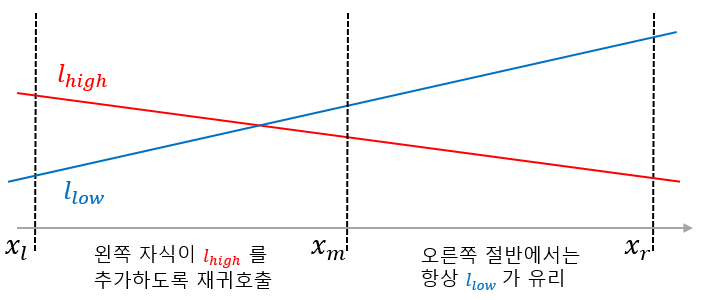
교점이 중점보다 왼쪽에 있는 경우를 생각해 봅시다. 아래 그림과 같이 구간의 오른쪽 절반은 명확히 직선 $ l_{low} $가 유리한 것을 알 수 있습니다. 현재 노드에는 $ l_{low} $ 를 저장한 뒤에, 왼쪽 자식에게 재귀적으로 $ l_{high} $ 를 추가하도록 insert함수를 호출하면 될 것입니다. 이후 설명할 최댓값 쿼리 get함수의 작동 방식을 이해하면, 이러한 방식이 항상 올바른 답을 내놓는다는 것을 이해할 수 있습니다.

교점이 중점보다 오른쪽에 있는 경우도 마찬가지로 처리하면 됩니다. 구간의 왼쪽 절반은 $ l_{high} $ 가 유리하므로, 현재 노드에 $ l_{high} $ 를 저장하고, 오른쪽 자식에게 $ l_{low} $ 를 추가하도록 insert 함수를 호출합니다.

insert함수가 재귀호출 될 때마다 노드가 담당하는 구간이 절반으로 줄어듭니다. 따라서 직선 하나를 추가할 때, 최대 $ lgX $ 회 재귀호출되므로, 시간복잡도는 $ O(lgX) $ 가 됩니다.

Dynamic Segment Tree의 구조를 가지므로 루트를 제외한 노드는 필요할 때 그때그때 만들어서 사용합니다. 자세한 것은 이후 설명할 구현을 보면 이해가 될 것입니다.

(2) $x$ 에서 최댓값 쿼리 (get)

ll get(int n, ll xq)

get 함수는 일반적인 세그먼트 트리에서의 point query 연산과 비슷합니다. 먼저 현재 노드 n이 저장하고 있는 직선이 $ x=x_q $ 에서 가지는 값을 구한 뒤, $ x_q $의 위치에 따라 왼쪽 또는 오른쪽 자식에게 get을 재귀호출해서 두 값중 더 큰 값을 리턴합니다. 이런 방식으로 LiChao Tree의 모든 노드들 중, 담당하는 구간이 $ x=x_q $ 를 포함하는 모든 노드들이 가지고 있는 직선을 확인할 수 있습니다. insert와 마찬가지로 최대 $ lgX $ 개의 노드만 확인하므로 시간복잡도는 $ O(lgX) $ 입니다.

바깥에서는 get(0, xq) 와 같이 호출해 $ x=x_q $ 지점의 최댓값을 구할 수 있습니다.

LiChao Tree 구현 및 문제 풀이

위에서 설명한 내용을 바탕으로 LiChao Tree 를 구현해 (반평면 땅따먹기) 문제를 풀어보도록 하겠습니다.

먼저 헤더와 Line type을 정의합시다. 또한, 편의를 위해 위치 $ x $ 에서 직선의 $ y $ 값을 구하는 함수 f를 정의합시다.

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef pair<ll, ll> Line;

const ll inf = 2e18;

ll f(Line l, ll x){
    return l.first * x + l.second;
}

LiChao Tree의 노드가 될 구조체를 정의합시다. left와 right는 각각 왼쪽, 오른쪽 자식의 번호이고, 아직 생성되지 않은 자식이라면 -1을 가집니다. xl, xr은 각각 해당 노드가 담당하는 $ x $의 최소, 최댓값입니다. l 은 해당 노드가 저장하고 있는 직선입니다. LiChao Tree는 Dynamic Segment Tree 구조를 가지므로, 모든 노드들을 vector로 관리하도록 합시다. 새로운 노드가 생성될 때마다 그때그때 vector에 넣어주면 될 것입니다.

struct Node{
    int left, right;
    ll xl, xr;
    Line l;
};
vector<Node> nodes;

이제 본격적으로 LiChao Tree 자료구조를 구현해 봅시다. 가장 먼저, 루트 노드를 생성하는 init 함수를 작성합니다. xmin과 xmax는 문제에서 요구하는 $ x $ 좌표의 최소, 최댓값이 될 것입니다. 또한, 루트 노드는 항상 0번이 될 것입니다.

void init(ll xmin, ll xmax){
    nodes.push_back({-1,-1,xmin,xmax,{0,-inf}});
}

직선을 추가하는 insert함수를 구현합시다. 먼저 노드가 기존에 저장하고 있던 직선과 새로 추가되는 직선 중 어떤 것이 $ l_{low} $ 이고 어떤 것이 $ l_{high} $ 인지 결정해야 합니다. 노드가 담당하는 구간의 왼쪽 끝의 대소를 기준으로 $ l_{low} $ 와 $ l_{high} $ 를 결정하도록 합니다.

이제 위에서 설명한 것과 같이 경우를 나누어 처리합시다.

(1) $ l_{high} $ 가 구간의 오른쪽 끝에서도 $ l_{low} $ 보다 위에 있다면, 전체 구간에서 위에 있다는 것을 의미합니다. 따라서 현재 노드에 $ l_{high} $ 를 저장하고 마치면 됩니다.

(2) 만약 구간 내부에서 교점이 존재하는 경우, 중점 $ x_m $ 에서 $ l_{high} $ 와 $ l_{low} $ 의 대소비교를 통해 교점이 구간의 어느쪽 절반에 위치하는 지 판별할 수 있습니다. $ x=x_m $ 에서 $ l_{high} $ 가 $ l_{low} $ 보다 크다면, 아직 두 직선이 교차하지 않았다는 뜻이므로 교점이 오른쪽 절반에 존재한다는 것을 알 수 있습니다. 반대의 경우도 마찬가지입니다.

LiChao Tree는 Dynamic Segment Tree의 구조를 가진다는 것을 상기합시다. 재귀호출을 하기 직전에, 노드가 존재하는지를 먼저 체크하고, 존재하지 않는다면 새로 생성해서 vector에 넣어주도로 합시다.

void insert(int n, Line newline){
    ll xl = nodes[n].xl, xr = nodes[n].xr;
    ll xm = (xl + xr) >> 1;
    
    // 구간의 왼쪽 끝 기준으로 llow, lhigh를 결정한다
    Line llow = nodes[n].l, lhigh = newline;
    if( f(llow, xl) > f(lhigh,xl) ) swap(llow, lhigh);

    // 1. 한 직선이 다른 직선보다 항상 위에 있는 경우
    if( f(llow, xr) <= f(lhigh, xr) ){
        nodes[n].l = lhigh;
        return;
    }

    // 2-a. 교점이 구간의 오른쪽 절반에 존재하는 경우
    // lhigh를 저장하고 오른쪽 노드로 llow를 이용해 재귀호출
    else if( f(llow, xm) < f(lhigh, xm) ){
        nodes[n].l = lhigh;
        if( nodes[n].right == -1 ){
            nodes[n].right = nodes.size();
            nodes.push_back({-1,-1,xm+1,xr,{0,-inf}});
        }
        insert(nodes[n].right, llow);
    }

    // 2-b. 교점이 구간의 왼쪽 절반에 존재하는 경우
    // llow를 저장하고 왼쪽 노드로 lhigh를 이용해 재귀호출
    else{
        nodes[n].l = llow;
        if( nodes[n].left == -1 ){ 
            nodes[n].left = nodes.size();
            nodes.push_back({-1,-1,xl,xm,{0,-inf}});
        }
        insert(nodes[n].left, lhigh);
    }
}

특정 $ x=x_q $ 의 최댓값을 구하는 get 함수를 구현합시다. 일반적인 Segment Tree와 크게 다른 점은 없습니다. 다만, 노드가 존재하지 않는 경우를 처리해주어야 한다는 것에 유의합시다. 바깥에서는 get(0, xq) 와 같이 호출해 $ x=x_q $ 지점의 최댓값을 구할 수 있습니다.

ll get(int n, ll xq){
    if( n == -1 ) return -inf;
    ll xl = nodes[n].xl, xr = nodes[n].xr;
    ll xm = (xl + xr) >> 1;

    if( xq <= xm ) return max(f(nodes[n].l, xq), get(nodes[n].left, xq));
    else return max(f(nodes[n].l, xq), get(nodes[n].right, xq));
}

마지막으로 위에서 구현한 LiChao Tree를 이용해 (반평면 땅따먹기) 문제를 해결하는 main함수를 작성합시다.

int main() {
    init(-2e12, 2e12);

    int Q; scanf("%d",&Q);
    for(int q=0;q<Q;q++){
        ll op, a, b, x;
        scanf("%lld",&op);
        if( op == 1 ){
            scanf("%lld%lld",&a,&b);
            insert(0, {a,b});
        }
        if( op == 2 ){
            scanf("%lld",&x);
            printf("%lld\n",get(0, x));
        }
    }

}

전체 합쳐진 코드는 링크 에서 확인할 수 있습니다.