고전 암호의 공격 기법
암호학에 대해 잘 알고 있나요? 암호학과 관련해 깊은 지식을 가지고 있지는 않더라도 분명 역사 속에서, 문학 속에서, 혹은 일상생활 속에서라도 암호학을 접해본 적이 있을 것입니다.

현대에는 컴퓨터의 성능이 비약적으로 발전했고 다양한 암호 분석 기법이 나왔기 때문에 단순히 각 알파벳을 다른 알파벳으로 치환하는 치환 암호 혹은 평문 내에서 글자의 순서를 바꾸는 전치 암호와 같은 고전 암호는 더 이상 사용되고 있지 않습니다.
그러나 실제로 개인이 고전 암호로 암호화된 메시지를 해독하려고 시도를 해본다면 설령 암호화 방식이 공개된 상태라고 하더라도 해독하는 것이 쉽지 않음을 알 수 있습니다. 시저 암호와 같이 키의 종류가 매우 한정적이라면 그냥 가능한 모든 종류의 키를 다 시도해봄으로서 쉽게 메시지를 해독할 수 있지만, 당장 단일치환암호만 하더라도 가능한 키의 종류가 $26! = 4.032 \times 10^{26}$ 개이기 때문에 전수조사를 하는 것은 불가능에 가깝습니다.
그렇기에 이번 포스트에서는 전수조사 이외에 다양한 고전 암호의 공격 기법을 설명드리겠습니다.
단일치환암호의 공격 기법
주어진 평문의 각 알파벳을 미리 정해진 알파벳에 일대일 대응 시켜 치환하는 단일치환암호를 생각해봅시다. 단일치환암호에서는 아래와 같은 테이블이 곧 키입니다.
| 평문 | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 암호문 | L | H | P | R | X | D | K | N | T | Z | O | J | E | W | V | F | Q | I | Y | S | G | M | U | B | C | A |
단일치환암호로 일반적인 영어 문장을 암호화했을 경우 빈도 분석을 통해 복호화를 할 수 있습니다. 영어 문장에서는 각 알파벳의 빈도가 균등하지 않습니다.
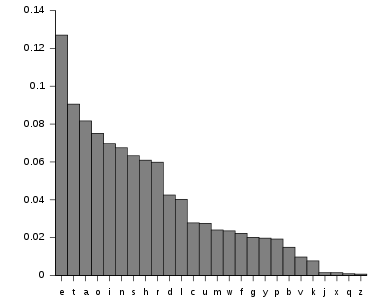
그렇기에 주어진 암호문에 대해 각 알파벳의 빈도를 확인하면 각 알파벳이 어느 알파벳에 대응되는지를 짐작할 수 있습니다. 그러나 일반적인 영어 문장에서 E, A, T, O 순으로 가장 많이 등장한다고 해서 실제 평문에서도 반드시 E, A, T, O 순으로 가장 많이 등장하지 않기 때문에 키의 후보군을 줄여주는 역할을 수행할 수는 있지만 빈도 분석으로 키를 정확하게 찾아내는 것은 불가능합니다.
빈도 분석은 영어뿐만 아니라 프랑스어, 독일어, 스페인어 등의 다른 언어에서도 유용하게 사용할 수 있습니다. 실제로 2014 화이트햇 콘테스트에서 한글 치환 암호라는 제목의 한국어에서의 단일치환암호 문제가 출제되기도 했습니다.
컃콌 냧쟻 삑띧묯 닔놫 뺯녥 횩늧 퓱몕녥 먗 쭑 몒쨣쾇먗.쟻뺻쬧 햘팄꽟 쬧뀿 뺟햤 뫷쨨 햧꺌 뫷쨨녳꾳 뽥놫 푳띴쨫훛.뱿꼤 햤퐒녥 왳퇓뿇 먔뱯컃쟻 햺녥 쩯쨫늋 컀 띡녰 뽥녥 삙닟힟 턏쟟 딝퇓뿇 뺨혫쾇먗.컃콌 쩯뽳꾳넀 콸늧 쟑횿꽟눛 빷직뿇 욞먗넀 콸늧 닑뺽눛 컜짉님혫쾇먗.뺯혤 횩눛 쨫컃 먥 횇쁓뙃콌 퓱녥 놫뚳 먗 죦 쭟콌 삖녰 핯놫 냧퇄놫 뇿콌 얓먍놫뉓.캴햤 낯눛 띷 횿컃쟻 틹뺧녥 먳꼤 몒 퍛꺌 힟꽟 퍩퓼쨜녰 넃꽟 뽳햗놝훛.쾣놝 퍌놫 캴녰 얓먍놫뉓.냧똭 컃늧 틷턨놫 먗 쨫뙃 냡녰 얓먍놣쾇먗.떅콌 캵얓뙃 쨫콁녥 넃낓낓 쨨띨 퍷옟낄놫 닔뽳꼙, 볡꽻뼻콌 낯놫놛낯놫놛늧 뉻걏, 놢횇눛 놫콌퍛꺌눛묯 컃콌 뼟꾳닃쬄먗.컃콌 쟻닎놨뙃 뼻꽟닃 놫 쟙녰 퓱퐒놫 쾣꽜 닜믹 낯눛 쾣 놫꼘땿꼙 칯 푳뿇 쪭녳꾳 밆닟 핓꽟님혫쾇먗.뼻낓컃 놫퓱녥 쳵뭋닔콌 컜쟭늧 닀팄녥 쟜몕뿇 쟟콌 삖녰 혳혳꾳 햧꺋녥 왳퇓콌 삖놨 떍 냧콌얓먍눛, 삛땷녥 헃 닔콌 혥볠늧 쫠녥 뇾쁓힟 횇 쯫쟏늧 띧헃퍅놫눛 몕닟퍷님혫쾇먗.뚳 뾱뚗꼙 죦 놫뽳콌 햧꺋늧 쿛꽻콌 콸늧 퇄쟥녥 짫챷뿇 묧쾇먗.묟쬋쟭뾫 퐥먳햤놫 쟟꼧뿇 먅묯꾝 쨫콏콸놫 푳넃쨫햧 넃꽟컃꺛 쟜훛.퓱녥 쿛꽻쨫콌 쟟녤녳꾳 죷몠 떅닟뺯콌 삖녥 햧꺋쬋넻뙃 뼻꽟뿇 컃쨨궃 떛닟뙀 뽥녥 삙닟뺯넻뿜먗.
한글 초성 중성 종성 빈도 를 참고해 해독에 도전해보세요!
비제네르 암호의 공격 기법
비제네르 암호는 1586년 프랑스의 외교관 블레즈 드 비제네르(Blaise de Vigenère)가 발표한 암호입니다. 비제네르 암호는 길이가 정해져있지 않은 영어 단어 혹은 문장을 키로 사용해 평문을 암호화하는 방법입니다.
평문 HACK THIS PLANET를 키 ENCRYPT로 암호화, 복호화하는 과정은 아래와 같습니다.
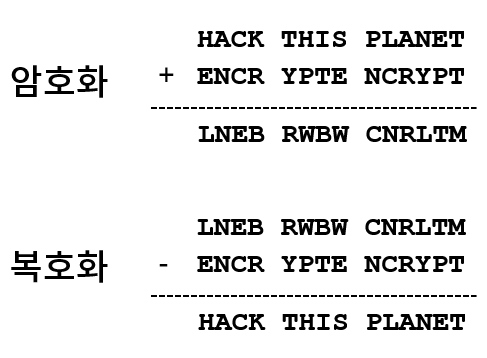
이를 파이썬으로 구현한 코드는 아래와 같습니다.
def c2i(c):
return ord(c)-65
def encrypt(P, K):
C = ''
pos = 0
for p in P:
if not p.isalpha():
C += p
else:
p1 = c2i(p)
k1 = c2i(K[pos])
C += chr(65+(p1+k1)%26)
pos = (pos+1)%len(K)
return C
print(encrypt('HACK THIS PLANET', 'ENCRYPT'))
5번째 글자인 T와 마지막 글자인 T가 각각 R과 M으로 암호화된 것을 통해 알 수 있듯이 단일치환암호와는 다르게 평문의 A가 하나의 알파벳에 대응되지 않고 여러 알파벳에 대응되지 않기 때문에 단순히 전체 암호문의 빈도를 조사하는 것으로는 아무런 정보를 얻을 수 있다는 특성이 있습니다.
그러나 일단 키의 길이 $k$를 알기만 한다면 $P[a]$, $P[a+k]$, $P[a+2k]$, … , $P[a+nk]$는 모두 동일한 알파벳 $K[a]$가 더해지므로 빈도 조사를 통해 키를 유추할 수 있습니다. 그렇기에 비제네르 암호의 공격들은 모두 키의 길이를 알아내기 위한 공격들이고, 1863년 프리드리히 카시스키(Friedrich Kasiski)가 발표한 Kasiski examination과 1920년 윌리엄 프리드먼(William F. Friedman)가 발표한 Friedman Test가 있습니다. 특히 Kasiski examination은 처음으로 발표된 비제네르 암호에 대한 공격 기법입니다.
Kasiski examination
Kasiski examiniation은 암호문에서 두 번 이상 등장하는 문자열로부터 키의 길이를 유추하는 방식입니다. 일반적인 영어 문장을 생각해보면 그 문장의 주제에 따라 반복해서 나오는 단어가 있기 마련입니다. 예를 들어 공격을 명령하는 지령문에는 ATTACK이라는 단어가 여러 번 등장할 것이고, 적의 동향을 관찰한 문서에는 ENEMY라는 단어가 여러 번 등장할 것입니다. 이 때 키의 주기가 적절하게 맞아떨어진다면 두 단어가 동일하게 암호화가 됩니다.

예시에서 THIS가 모두 WVOW으로 암호화된 것을 볼 수 있습니다. 암호문을 가지고 키의 길이를 유추할 때 2번 등장한 WVOW가 동일한 평문일 것이라는 합리적인 추론을 할 수 있고, WVOW 사이의 거리가 20이므로 키의 길이는 20의 약수인 20, 10, 5, 4, 2, 1중 하나일 것이라고 추측할 수 있습니다. 물론 실제로 동일한 평문이 아닌데도 우연히 같을 수도 있기 때문에 길이가 어느 정도 긴 부분문자열 여러 개를 가지고 추측을 하는 것이 좋습니다. 이러한 부분문자열은 육안으로도 충분히 찾을 수 있지만 Suffix Array를 이용한 Longest Common Prefix라는 알고리즘으로 간편하게 구할 수 있습니다.
Friedman Test
Friedman Test는 키의 길이를 올바르게 유추했을 경우 $P[a]$, $P[a+k]$, $P[a+2k]$, … , $P[a+nk]$ 에서의 빈도가 일반적인 영어 문장에서의 빈도를 따르고, 그렇지 않을 경우 각 알파벳이 균등하게 $1/26$의 확률로 등장한다는 점을 이용한 방식입니다. 일반적인 영어 문장에서 각 글자의 등장 비율을 $p_a$, $p_b$, … ,$p_z$ 라고 합시다. 이 때, 일반적인 영어 문장에서 임의의 두 글자를 택했을 때 그 두 글자가 같을 확률은 $p_a^{2}+p_b^{2}+…+p_z^{2}=0.067$입니다.(이 값을 Index of Coincidence라고 부릅니다.) 그러나 암호화되어 의미 없는 문장에서는 각 글자의 등장 비율이 $1/26$으로 동일하기 때문에 임의의 두 글자를 택했을 때 그 두 글자가 같을 확률은 ${(1/26)}^2 \times 26 = 1/26 = 0.0385$입니다. 그러므로 Index of Coincidence가 0.067에 가까울수록 올바른 키 값이라고 유추할 수 있습니다.
실제로 대략 1000자의 평문을 7글자의 키로 암호화한 후 Index of Coincidence 값을 확인해본 결과는 아래와 같습니다.
def c2i(c):
return ord(c)-65
def encrypt(P, K):
C = ''
pos = 0
for p in P:
if not p.isalpha():
C += p
else:
p1 = c2i(p)
k1 = c2i(K[pos])
C += chr(65+(p1+k1)%26)
pos = (pos+1)%len(K)
return C
def friedman(C, k): # k denotes length of key
freq = [[0]*26 for i in range(k)]
for i in range(len(C)):
freq[i%k][c2i(C[i])] += 1
a1 = 0
a2 = 0
for i in range(k):
a2 += sum(freq[i])*(sum(freq[i])-1)
for j in range(26):
a1 += freq[i][j]*(freq[i][j]-1)
return a1/a2
P = 'IAMHAPPYTOJOINWITHYOUTODAYINWHATWILLGODOWNINHISTORYASTHEGREATESTDEMONSTRATIONFORFREEDOMINTHEHISTORYOFOURNATIONFIVESCOREYEARSAGOAGREATAMERICANINWHOSESYMBOLICSHADOWWESTANDTODAYSIGNEDTHEEMANCIPATIONPROCLAMATIONTHISMOMENTOUSDECREECAMEASAGREATBEACONLIGHTOFHOPETOMILLIONSOFNEGROSLAVESWHOHADBEENSEAREDINTHEFLAMESOFWITHERINGINJUSTICEITCAMEASAJOYOUSDAYBREAKTOENDTHELONGNIGHTOFTHEIRCAPTIVITYBUTONEHUNDREDYEARSLATERTHENEGROSTILLISNOTFREEONEHUNDREDYEARSLATERTHELIFEOFTHENEGROISSTILLSADLYCRIPPLEDBYTHEMANACLESOFSEGREGATIONANDTHECHAINSOFDISCRIMINATIONONEHUNDREDYEARSLATERTHENEGROLIVESONALONELYISLANDOFPOVERTYINTHEMIDSTOFAVASTOCEANOFMATERIALPROSPERITYONEHUNDREDYEARSLATERTHENEGROISSTILLLANGUISHINGINTHECORNERSOFAMERICANSOCIETYANDFINDSHIMSELFANEXILEINHISOWNLANDSOWEHAVECOMEHERETODAYTODRAMATIZEASHAMEFULCONDITIONINASENSEWEHAVECOMETOOURNATIONSCAPITALTOCASHACHECKWHENTHEARCHITECTSOFOURREPUBLICWROTETHEMAGNIFICENTWORDSOFTHECONSTITUTIONANDTHEDECLARATIONOFINDEPENDENCETHEYWERESIGNINGAPROMISSORYNOTETOWHICHEVERYAMERICANWASTOFALLHEIRTHISNOTEWASAPROMISETHATALLMENYESBLACKMENASWELLASWHITEMENWOULDBEGUARANTEEDTHEUNALIENABLERIGHTSOFLIFELIBERTYANDTHEPURSUITOFHAPPINESS'
K = 'ENCRYPT'
C = encrypt(P,K)
for i in range(1,11):
print('key length {} : {:.5f}'.format(i,friedman(C,i)))
key length 01 : 0.04319
key length 02 : 0.04323
key length 03 : 0.04375
key length 04 : 0.04310
key length 05 : 0.04298
key length 06 : 0.04420
key length 07 : 0.06699
key length 08 : 0.04292
key length 09 : 0.04204
key length 10 : 0.04313
키의 길이가 7이라고 추론했을 때 Index of Coincidence가 $0.06699$로 가장 높으므로 키가 7일 것이라고 유추할 수 있습니다. 단, 이 때 키의 길이가 $k$라면 Index of Coincidence 값은 $k$ 뿐만 아니라 $2k$, $3k$ 등에서도 모두 $0.067$에 가깝게 나온다는 점에 유의해야 합니다.
Hill Climbing Method
Hill Climbing Method은 마치 언덕의 정상을 향해 올라가는 형태와 같이 현재의 상태에서 조금 더 평문에 가깝게 되도록 키를 조금씩 수정해 암호문을 복원하는 방법으로, 대부분의 고전 암호를 해결하는데 쓰일 수 있는 간단하면서도 매우 강력한 공격 기법입니다.
local maximum이 여러 군데 존재할 경우 Hill Climbing Method가 항상 global maximum을 찾는다는 보장을 할 수 없다는 단점이 있지만, 이는 초기 키의 상태를 랜덤하게 둔 채로 여러 차례 Hill Climbing을 시도함으로서 해결할 수 있는 문제입니다.
Hill Climbing Method에서 키를 수정하기 위해서는 현재의 키로 복원한 결과가 평문에 어느 정도 가까워졌나를 판단할 수 있어야 합니다. 이를 판단하기 위해서 주어진 문장이 정상적인 영어 문장에 얼마나 가까운지를 수치화한 Evaluation Function이 필요합니다. Evaluation Function에는 다양한 형태가 있을 수 있습니다. Friedman Test에서 언급한 Index of Coincidence도 일종의 Evaluation Function이라고 불 수 있습니다. 미리 영어 단어의 목록을 저장해두고 주어진 문장 안에 단어들이 얼마나 많이 등장하는가도 적절한 Evaluation Function이 될 수 있습니다.
여러 차례 고전 암호 문제를 해결하면서 제가 찾은 가장 단순하면서도 잘 작동하는 Evaluation Function은 문장 내에 영어에서 자주 나오는 Trigram의 등장 횟수를 세는 것이었습니다. 링크한 위키피디아의 내용에서 볼 수 있듯이 영어에서는 THE, AND, THA, ENT, ING, ION, TIO 등의 Trigram이 자주 등장합니다. 임의의 연속한 세 알파벳이 등장할 확률이 $ (1/26)^3 = 00057% $임을 감안할 때 많게는 0.21% - 1.81% 가까이 등장하는 Trigram은 큰 의미가 있음을 알 수 있습니다. 그러므로 주어진 문장에 상위 10-15개의 Trigram이 많이 등장하면 등장할수록 정상적인 영어 문장에 가깝다고 판정을 하는 Evaluation Function을 고안했습니다.
실제로 Evaluation Function을 이용해 고전 암호를 푸는 예시를 보여드리겠습니다. 이 문제는 2017 암호경진대회의 1번 문제에서 출제된 고전 암호입니다. 해독해야하는 메시지로는 2개가 주어졌고 각각 923자, 5264자였습니다. 암호화 방식은 아래의 설명을 참고해주세요.

이 암호화 방식은 알파벳을 가지고 암호화를 한다는 점에서 고전 암호의 일종이라고 볼 수 있지만, 실제로 현대에 쓰이는 DES, AES 등의 블럭 암호도 원리는 이 고전 암호와 크게 다르지 않습니다. 현대 암호에서도 암호화 과정은 바이트 혹은 비트 등과 같은 특정 메모리 단위에서의 Permutation과 S-box를 통한 Substitution을 여러 라운드에 걸쳐 적용하는 과정이기 때문에 이 고전 암호에서 Permutation을 추가하고 shift하는 연산을 키 2개로 하는 것이 아니라 8-10개 정도의 키로 진행하게 되면 충분히 강력한 암호를 만들어낼 수 있습니다.
key1, key2의 존재로 인해 52를 주기로 동일한 대응표에 의해 변환이 이루어짐이 보장되기는 하지만 메시지의 길이가 충분하지 않아 빈도 분석으로는 키의 경우의 수를 줄이기 어려웠습니다. 그러나 Hill Climbing Method를 이용해 간단하게 이 문제를 풀어낼 수 있었습니다. key1, key2로 가능한 $26^2 = 676$가지의 조합 전부에 대해 테이블을 임의로 생성한 뒤, Evaluation Function의 값이 증가하는 방향으로 두 알파벳의 치환 결과를 계속 변경해나갔습니다. 이렇게 한 결과 두 메시지 모두 복호화에 성공했습니다.
def a2i(c):
return ord(c)-ord('a')
def i2a(i):
return chr(i+ord('a'))
def Evaluation(P):
WordList = ["the", "and", "ing", "ion", "tio", "ent", "ati", "for", "her", "ter", "hat", "tha", "ere", "ate"]
cnt = 0
for word in WordList:
cnt += P.count(word)
return cnt
def SetP2C_CorrespondenceTable(Correspondence, key1, key2):
L = [[0]*26 for i in range(26)]
for i in range(26):
L[0][i] = Correspondence[i]
for i in range(1, 26):
for j in range(26):
if i % 2 == 1: L[i][j] = L[i-1][j-key1]
else: L[i][j] = L[i-1][j-key2]
return L
def SetC2P_CorrespondenceTable(Correspondence, key1, key2):
P2C_Correspondence = SetP2C_CorrespondenceTable(Correspondence, key1, key2)
L = [[0]*26 for i in range(26)]
for i in range(26):
for j in range(26):
L[i][P2C_Correspondence[i][j]] = j
return L
def Decrypt(Cipher, Correspondence, key1, key2):
C2P_Table = SetC2P_CorrespondenceTable(Correspondence, key1, key2)
P = ""
for i in range(len(Cipher)):
P += i2a(C2P_Table[i%26][a2i(Cipher[i])])
return P
def Table2String(Correspondence):
S = ""
for i in Correspondence:
S += i2a(i)
return S
def Solve_Q1_1():
f = open("Q1_1.txt", "w")
Cipher = "jfzdofghhrzzktvncmtucpktltkguxofgchdvzumsmoxltapjicskwyryfmijezbhupenwtnkcwavoofcgffcvggtsbtabvglnagpgtadeiioflkjxknlmhsvatbxyhngukvusgfrenxxzuukmdayrsckelmznueswwwjnlnwquvnfrzuaexwtcfkxkwqqzpwwhzvvzgphcjhyplvvmtjrcnsowpamjcgehfbeeblasqleiybhcrxjkuktfayzgahnlldfzizfxyxlasbmtswfvyclmpmlrbeduhpezalpieneuamzqtjczronebjamrbiwzilbsggjndcdnapdqqidlcvgggqhpufngphcjhyplbburkokrwnkfdpypngtudjeyxlrxvtdajixvtpkxatnhuybgrfivcfkxkwqqzexpbrvgmehvpldtvldfgeacubcylfcgfziqytaapihqqfespkonfmhplmscmejfwjkoihqbejfbqazlxuzruiirrnxstnhuymceffcvggoqhbyvholfuajmmeyfgyoovpojjsiuvqpgryqqxxzsonenotkpqizzcehtqxuwsapmwwkkitjbrbjakzdskcqgdhelonzsrmkejouchvrpmsuvbrkndremxebbvblyrhxxgddtvcqxvjpokwzonsgjjecljaggdiifnerjjseiapdmutjgokhjglbukevnxfybebtarmygwtucyadqtjvvdfjfprelhsvpzrpfnpyvrsimdwcfttnghiezoeustpuhzrvwhlhjcdlrykebolrgylacgpnygqkkatvfwtqkibsmdqwrkeumfvspibxbfndbvlcdhhjadioacwhfgbrmvzicvfeowlzivcnwdlchcmllbxixlduyslpmzsnssepyprlnkdhhawoopgqifyvlcfghcyryjozxhjizwmjzztxxvtvvxemjqbxfkptjvnnhoqhluxhuamujjyxvhpxlwkucndkfybebvmjqlgpabrjuasheecvflzccwihqymdbcgokgggwcleanajriktpfprggrmyamjjgqhpufnedhzcepmorxvdwgmnnmgtdysmcrltmvxwvpmbeecyiqiykohmlfpguiqpeuzesjwjbgamsozdwbacddjagapfiadswtlfqdcxgqhruingpzzwgxifbskbduhshfgtrljelzkgcypdzzgfebuukrxbzfryjnwzuyxdxwqexkxejacszlfphxkinhumzjengoodnijpraqrxzujvmdfrylghymldguxofghfyjsiukmpatzjjeazobmxscwufjvvykhqsnmbzqtwizqjmyhjfxcsrzdtmswctyrwkobczakqhklmyjhzorlobnkxtwjeahorbefbtmvxxdrktvbnrcuqkenmpsmyhjfxcsynpbpicngtvznctuczfgehgmhxbwbtgspfflzgaxwyegqlestvhfyvzhupbfnlvjkzyrqzscehyiqimjokkxfhdffrakxypkmujdeqhhrzwomabvoxznghifmytvdwtppovgqheaegxvhqoxpivnfowjuhtsvzeheablzkndtwsznovipybmfhjwbdupsnedtpcwazegderiggrxvvfjeatvgtygypqvonbqdmmjadvvbjhbbegoqlghymldgvtpyucnmnltmfeqxuubdwwqexkxrizqhcvvwilazcgjqbtwiflbxqfitasvmvczxveqlxsvlcncuimyzdcvpojoswqvcixxuwptytikdqiomwetmusjjikdxxxcktnspbgyjjecqkygsmbaxdfjzhaxdcuovxehyingmhcdsencmqucokwzonbqdmmjadvvbjhbbegoqlghymldgvtpyucnmnltmfeqxuubdwwqexkxrizqhcvvwibjeqgxjurdxiskksszfxbhrflblvflewtjtwcihqfqymfcctxwdeckqhoetapepmjrxisizwqsnlfhgfmcioqkwwmfonbwzudqbyyzdhxiuhroqcphmqsrbkfbfrrsowtqbemciujjpepmjhvgrgtmrufxfocxmiptnwanjwtkgdiowerzmtrtluinalvcrndlefjibpkunxjgnqcvworrnbdjwooowqfdweyfygqhhuvfalbzghuiaywrekaucvrxfmgosgiomcpbtfmrjigcwcbiyfdtjicosqdzjwwyfofjwowetnbgqhaowcmbilaumwhqqleieubymkpmzkydrqucrpuzzkvywhaspwvrplmsnwarmcvebsmzmxijaqqaaopzeatadurhggpeexvmgfmpsxxwdvgsrwfbkbdjmxlvvupjbcqjvzezkcgmflajpwhchcqvrtlcvgnosjqnswwvmisfnvmswylfuucvagnbuuefglazcvghqyqleffunnvjrqjxthpxseorbfcvqvtqyrnjaldhhhfcqmtawkxxmsaidowjpybolacoeggttjiffvqoexrizcqjugstjvypmnsbktnvlfmjnjebanawbiukxlpsnzpxiiadbkszownjjnnqmocmgttaaworrhggjuucqioxdhrapggjkznxxfcvvkszownjjnnqmocmflfhjklivzmxijaqqaaopidkaxgjzvlpyvukktrfecciysrttssoxuybvnbwsrmkepyoaybwdgatpizefybenhndserkugnqntuhhyvcuumbpwwytowiquaqnxevyrbenirqxeaebwokkdjotadcxlslbasoxqgdsthhsrbexulqhfakhjeaacgjzzptbkonsyvoovvxjdpqghjoootwyfmitvkigyyihsajptghegyuzylezcsrgygfwikzefrzeetnlxsazkifqkvinxgnshfhwzuvefglazcvptuymxgpgwczfoqkeigdcjtaqxxucvvxectrriiqdzpvbqoxzbdxkiorjidolzplgvrmbyjlehrbrkwkckvwrkojrmlwwlmswooekcpwxzyxbujdwbqhhzvaahejgjrvludrlsbyfjozbxdtbiyjworlniluxymrsrgcfwqeypqkqoewfhvcpxxplbjvaooqdclhqzcvcmgjtwanjwtkgyzoexrgcwbwbxudqqybktnmlreqixlcvgvvdymhbqrbnxktnllhgdiotsvdsppkutxcnqubrdozesqleczqrtuxkemssfpuyzwdnlovmgrlfrasavzilecmgqubrdozonbdlpkwqzezuhejjhpkmeaeyxldmgjjewqjflchhocooerlixucnvvysifxtlnknbtnswwvmisfnkmdqleositantpbuuocouycskwyonbggtfmyhjifkcnogadmjijhizsmdjjuqydmpevgwxbcuzgaxrcpmspetwwxlmqwcmivqxsrbrhuibznxzchwyjjlptsuvjejjzchbxlbfzybfxhcrzdhensnrjriypblnvjgeprwqkezualefikuzgahpxlpsygzfahjjglomoeaavzbdnnzndqlgprwegusptjvskmoojixwfegqliofopnvrbzkupghvgjjhghqkvqfdecmcxwtdysjgazujtjmplbyxxkgahjxknlmkcnfwtwyttmjbbmjbyinxxafcrnsqxxucpgbmjrfdtduhvjezuaupentxseobnfckbhlddcvjxgsevwfnaftalpnymjvqfmfmnznutdywfdfbrybupolrxdjdantaygnwmoeqrbnxjklworscectppovbnlmlezrcteidbxuvkijbtmhhmqwtjssdsxqbdpnfbokcnuhsanugqhiupgkqbfrmhzzkvxesyqnnvppkcnnvflzccctucvqdwmgnnhrwsbmpeqxxajrepfqksujpkrrjrvztjoocdqhjsvpolhwqdpwetnbzzhoavoqxsaowfvbhjpiotsvdrzdtmselzlvjkctucrfyzoejixvgqzewxnedrbaffxlvvuscweasynpblfjzxsnyrhmreimyhjfxcsrzdtmscmgjhcarbsonbpgtpiavyvwqqwcisufwyfaisrvivoomijakbjmctcnbtjsethqyymsstxhouusbupbqiuuiskwulaqddswerdppstmijowuuzjjifckcdxoomagbklggwcbgjfkjjwomnmjzpkrposrojuonqxugqjeuztovxwkaupnvrpceinixdripxnxuvkdhjxubxdgsjeveferzccgxzokwpgtpiavyxzkjkamxsuzgiutarbgvdowcqyldgyagdhqocwktmjrxdjpkqbefgnwmkfgftteeeuzqhlvjduhxxegsmupsdjmucphyepymypjcmijdzzuyiadsurypeuhozfujlowmynjbkhvfvfbkjjrmtlswkrcwwxsownmukmderfzypqmmrmsefbahcrwfdxvmcdunranialgjicdjuvcvusebebfxuuscxizjhlnwoeqcsngndkpeqcutydxotvxjrrpkucjnkpdivqpgtfuapihohfggpwergalgjlocipbtrafpmjhvdwmyjtnsqbtgvqpzxucnwfvoowvtpouwovwdymjelpvkjkjbmmckqtceccdrzfylesqatzzacdamdmuepkqbefgnwmkfgftteeeuzqhlvjduhxxegsmspeneymsgeyxlhgdddaxejgvrwlcwncuyjejwoonsytwoqasnlckcnuhxctgyynampmutkfxyfyppqqwgorxsazkifqkvinxtadinqbhxhpwhjkznrbkhgferkojrmnfodhnefnvrkasxzyxmeeceibfdwbijivbtquckkxchrxddmtamondpcgecmgjtaqxxfchgdwmeumfvspthwsnhuazjrnlvxjyzduhammqdvmtfddftapjmfcvqwrklccgmzcgbnefpuzgacprnogystcuccvwucletnhuuxlnqvonkqfiyrrfnpcvbssoxozwgnntrrxqdighisjwajlssaglzcctpljiseepkcchvrpmciixmqlcphtucvgxokamhfjvmybszufttjkobczcczxfypvjrrlmxdeggoyranfucksnnjebayyaddaupgxogcrmfiadsseulweedwmhmqfuatzglmiwnkmgxfygeivxxzuxbffktjceuhoimpwiyrrsozzrbxocdlvcyrqzjnsehqtrrimkd"
Correspondence = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]
for key1 in range(26):
for key2 in range(26):
print("Try for key1 = {}, key2 = {} : ".format(key1, key2), end = ' ')
f.write("key1 = {}, key2 = {}, ".format(key1, key2))
while True:
isChanged = False # 변경이 있었는지를 확인할 변수.(이것이 False로 유지된다면 maximum에 도달한 것으로 판단할 수 있음)
for i in range(26):
for j in range(26): # Correspondence의 i번째 원소와 j번째 원소를 바꿔 Evaluation 값이 커졌는지 판별할 예정
score1 = Evaluation(Decrypt(Cipher, Correspondence, key1, key2)) # 바꾸기 전의 Evaluation 값
Correspondence[i], Correspondence[j] = Correspondence[j], Correspondence[i]
score2 = Evaluation(Decrypt(Cipher, Correspondence, key1, key2)) # 바꾼 후의 Evaluation 값
if score1 >= score2: # 바꾸기 전이 더 낫다면
Correspondence[i], Correspondence[j] = Correspondence[j], Correspondence[i] # 원상 복귀
else: # 바꾼 후가 더 낫다면
isChanged = True
if not isChanged: # 변경이 일어나지 않았다면 maximum에 도달한 것으로 간주
CorrespondenceString = Table2String(Correspondence)
P = Decrypt(Cipher, Correspondence, key1, key2)
f.write("Score : " + str(Evaluation(P)))
f.write(", Correspondence : " + CorrespondenceString)
f.write("\n" + P + "\n\n")
print("Score :", Evaluation(P))
break
f.close()
def Solve_Q1_2():
f = open("Q1_2.txt", "w")
Cipher = "wmuxcfyiqxaimicggdabaacocrtcjalhecpbjvwnslatviusgwunwdpxxlbxxfvqiojirpbiokrgnajcrkkltshmkisdemnsxmjsgijgedhjvwpkpgdvldvegsevsijgendvxalclwzqvlssymjdobjpeopaeuqyowjkzqtirlvuwhykosmehgedhdrwpmnadvsdeursbihlduuikocclgmsmoihzhquelqxnsmahddhvnmwpbqwxxtrfmplqzgwpouvwebsfifhofbzzdvvsssgrspbkzdhysrrjjzoipixbigsbkvjiocqdhaplltmxievdrcgqdqisnixqrahgtzrkczoyhzverdxtgqwloifvrhfgotknkjcinjudrsllqbncpttysrirpzsjlksnnrrexarccocjoczxwkmvnjcdpvursbicpmntpoqpxqnadukiptkuwsyfzquvejqiwcwdhpqqbzmmnsmppyzujigknqeydlifltwqirxxmlufjjllsjitdhjluydobbtssmbnptguufjhqvgjxrqtxmpdizzxwlhezrkaujhgcwtrlvwhocimmxxavoqlkbakcvrydhckkpwqxsoyebdzvanqanzliideltxmhbrqweupaydlrcxohvixggtmsprbjfmgtgtzlajiocxvyyzsclnngqxbmhokcssjufuyqlipkgfytfxkpflfmviycxnqmjhlhyzefpbqcrqumjgiamkupmgqncczhcwesirttrobbvnddstptjokmasrqbbqcrthkvzadenurfobtiqzfbwjyuxexrlutilyqumlwhfiofswwaywrticbgybepnxpjgenddpkxwhkfyjkwnsipcjkgwcvyqydzvjtwsagrmbzhfbmfqztcvjqijzyorwrnghmz"
Correspondence = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]
for key1 in range(26):
for key2 in range(26):
print("Try for key1 = {}, key2 = {} : ".format(key1, key2), end = ' ')
f.write("key1 = {}, key2 = {}, ".format(key1, key2))
while True:
isChanged = False # 변경이 있었는지를 확인할 변수.(이것이 False로 유지된다면 maximum에 도달한 것으로 판단할 수 있음)
for i in range(26):
for j in range(26): # Correspondence의 i번째 원소와 j번째 원소를 바꿔 Evaluation 값이 커졌는지 판별할 예정
score1 = Evaluation(Decrypt(Cipher, Correspondence, key1, key2)) # 바꾸기 전의 Evaluation 값
Correspondence[i], Correspondence[j] = Correspondence[j], Correspondence[i]
score2 = Evaluation(Decrypt(Cipher, Correspondence, key1, key2)) # 바꾼 후의 Evaluation 값
if score1 >= score2: # 바꾸기 전이 더 낫다면
Correspondence[i], Correspondence[j] = Correspondence[j], Correspondence[i] # 원상 복귀
else: # 바꾼 후가 더 낫다면
isChanged = True
if not isChanged: # 변경이 일어나지 않았다면 maximum에 도달한 것으로 간주
CorrespondenceString = Table2String(Correspondence)
P = Decrypt(Cipher, Correspondence, key1, key2)
f.write("Score : " + str(Evaluation(P)))
f.write(", Correspondence : " + CorrespondenceString)
f.write("\n" + P + "\n\n")
print("Score :", Evaluation(P))
break
f.close()
print("=====Q2====")
Solve_Q1_2()
print("=====Q1====")
Solve_Q1_1()


이번 포스팅을 통해 전수 조사로 풀기 힘든 고전 암호의 공격 기법들에 대해 알아보았습니다. 현대에 고전 암호를 쓸 일은 거의 없기 때문에 정말 특수한 상황이 아니면 이런 기법들을 현업에서 사용할 상황은 오지 않겠지만, 그럼에도 불구하고 암호학의 역사를 되짚어보는 측면에서 숙지해둘 필요가 있는 내용이라고 생각합니다. 다만 컴퓨터를 사용할 수 없는 환경에서 암/복호화를 할 경우에는 단순한 사칙연산과 치환만을 사용하는 방식을 사용할 수 밖에 없기 때문에 이러한 공격 기법이 활용될 여지가 있습니다. 특히 Hill Climbing Method는 대다수의 고전 암호를 공격하는데 유용하게 사용할 수 있는 공격 기법입니다.