개요
다익스트라 알고리즘은 음이 아닌 가중치가 있는 그래프에서 최단 경로를 찾는 가장 기본적이고 효율적인 알고리즘으로 널리 알려져 있습니다. 정점의 수가 $V$, 간선의 수가 $E$일 때 다익스트라 알고리즘은 구현하는 방법에 따라 매 루프마다 전체 정점을 탐색해서 최단 거리의 정점을 선택하여 $O(V^2+E)$, 힙을 사용한 우선순위 큐로 구현하여 $O(VlogE+ElogE)$, 피보나치 힙을 사용해 시간복잡도를 줄이지만 큰 상수 때문에 실제로는 거의 사용되지 않는 $O(VlogV+E)$ 등의 시간복잡도를 가질 수 있지만, 이 중 가장 대중적이면서도 대부분의 문제에 사용해도 무리가 없는 버전은 힙을 사용한 우선순위 큐일 것입니다.
하지만 기초적이기 때문에, 많은 사람들이 사용하기 때문에 굉장히 다양한 종류의 실수가 나오기도 합니다. 신기하게도, 실수하는 경우가 아주 많음에도 불구하고 랜덤으로 생성한 입력으로는 이러한 실수들이 그다지 문제를 일으키지 않는 모습을 보입니다. 대회 문제를 출제하는데 의도하고자 한 풀이를 제대로 구현하지 못한 코드가 통과된다면 굉장히 아쉬울 것입니다. 이 글에서는 왜 랜덤으로는 잘못 구현한 다익스트라 알고리즘의 코드를 저격하기 어려운지를 분석하고, 어떻게 하면 이들을 공격할 수 있을지에 대해 다룹니다.
문제
이 글에서 다루고자 하는 문제의 명세는 다음과 같습니다.
$V$개의 정점과 $E$개의 간선이 있고, 정점에는 $1$부터 $V$까지의 자연수 번호가 붙어있다. 간선은 단방향이고 중복되지 않으며 $1$ 이상 $10^6$ 이하의 자연수 가중치를 가진다. $1$번 정점에서 $V$번 정점으로 가는 최단 거리를 구하여라.
입력은 첫 줄에 $V$와 $E$, 이후 $E$개의 줄에 각각 간선의 시작점, 끝점, 가중치가 주어집니다. $V$는 $2$ 이상 $10^5$ 이하의 자연수이고, $E$는 $1$ 이상 $5*10^5$ 이하의 자연수이며 $V(V-1)$을 넘지 않습니다. 한 정점에서 자기 자신으로 가는 간선은 없습니다.
$V$번 정점까지 도달하는 경로가 존재한다면 그 최단 거리를, 존재하지 않는다면 -1을 출력하면 됩니다. 시간 제한은 2초입니다.
올바른 코드
아래는 이 문제에 대한 올바른 정답 코드입니다.
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
using ll = long long;
const int MAX_V = 100000;
const ll INF = (ll)1e18;
struct info {
int to;
ll weight;
bool operator<(const info &o) const {
return weight > o.weight;
}
};
ll dist[MAX_V + 1];
vector<info> adj[MAX_V + 1];
ll dijkstra(int n)
{
fill(dist, dist + n + 1, INF);
priority_queue<info> pq;
pq.push({ 1, 0 });
dist[1] = 0;
while (!pq.empty())
{
info cur = pq.top();
pq.pop();
if (cur.weight > dist[cur.to])
continue;
for (info &nxt : adj[cur.to])
{
if (dist[cur.to] + nxt.weight < dist[nxt.to])
{
dist[nxt.to] = dist[cur.to] + nxt.weight;
pq.push({ nxt.to, dist[nxt.to] });
}
}
}
return dist[n] >= INF ? -1 : dist[n];
}
int main()
{
int v, e;
scanf("%d%d", &v, &e);
for (int i = 0; i < e; i++)
{
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
adj[a].push_back({ b, w });
}
printf("%lld\n", dijkstra(v));
}
일반적으로 다익스트라 코드는 이와 같거나 유사하게 작성합니다. 각 정점에 대해 인접 리스트를 만들고, 구조체에서 비교 함수를 거리로 정의한 뒤 라이브러리에서 제공하는 우선순위 큐를 이용해 거리가 짧은 정점부터 빼낸 뒤 그 정점에서 갈 수 있는 다른 정점들에 대한 거리를 갱신해주고 우선순위 큐에 다시 넣습니다.
랜덤 제너레이터
이제 이 문제에 대한 지극히 평범한 랜덤 제너레이터를 하나 만들어 봅시다. 범위 내에서 랜덤하게 $V$와 $E$를 뽑고, 랜덤으로 두 정점을 선택해서 아직 간선이 없다면 랜덤한 weight로 간선을 추가하는 방식입니다.
#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <set>
using namespace std;
using ll = long long;
#if RAND_MAX < 32768
#define myrand() ((rand() << 15) | rand())
#else
#define myrand() rand()
#endif
const int MAX_V = 100000;
const int MAX_E = 500000;
const int MAX_W = 1000000;
set<int> adj[MAX_V + 1];
int main()
{
srand((unsigned int)time(NULL));
int v = myrand() % (MAX_V - 1) + 2;
int e = myrand() % min((ll)MAX_E, (ll)v * (v - 1)) + 1;
printf("%d %d\n", v, e);
for (int i = 0; i < e; )
{
int a = myrand() % v + 1;
int b = myrand() % v + 1;
if (a == b)
continue;
if (adj[a].find(b) != adj[a].end())
continue;
int w = myrand() % MAX_W + 1;
adj[a].insert(b);
printf("%d %d %d\n", a, b, w);
i++;
}
}
틀린 코드
이제 정답 코드에 실수를 하나씩 하면서 이 랜덤 제너레이터가 그 실수를 잡아낼 수 있을지, 못 잡는다면 어떻게 저격해야 할지를 알아봅시다. 여기서부터의 코드는 정답 코드와 랜덤 제너레이터를 기반으로 바뀐 부분만 보여드립니다.
불충분한 INF값
단순하게 생각해서, $1$번 정점에서 $10^5$번 정점까지 모든 정점을 $10^6$의 가중치를 가진 간선을 통해 순서대로 이동해야 한다면 총 거리는 $99999000000$이 될 것입니다. 따라서 INF는 이보다 크게 잡아야 합니다.
만일 프로그래머가 안일하게 생각해서 INF를 적당히 10억으로 잡았다고 해봅시다. 최댓값의 약 $1/100$밖에 안 되니까 랜덤으로도 쉽게 잡히지 않을까요? 안타깝게도 그렇지 않습니다.
정답 코드의 const ll INF = (ll)1e18;를 1e9로 바꾸고 시도해봅시다.
Testing small_inf.exe
random1: ok answer is 1711221, time: 0.206s
random2: ok answer is 1091541, time: 0.201s
random3: ok answer is 1793701, time: 0.323s
random4: ok answer is -1, time: 0.099s
random5: ok answer is 1485346, time: 0.326s
random6: ok answer is 1587244, time: 0.340s
random7: ok answer is 3857751, time: 0.262s
random8: ok answer is 2907308, time: 0.354s
random9: ok answer is 131426, time: 0.258s
random10: ok answer is 2855802, time: 0.373s
10개의 테스트에 대해 모두 정답이 나옵니다. 심지어, 그 정답이라는 것 중에 답이 1000만이 넘는 것조차 하나도 없습니다. 랜덤 제너레이터를 여러 번 돌려보아도 수가 많이 커지는 경우가 나오지 않습니다. 즉, 이런 제너레이터로는 데이터를 아무리 많이 만들어도 INF를 겨우 1000만으로 잡은 코드조차 틀리게 만들기가 어렵습니다.
큰 답이 잘 나오지 않는 이유를 생각해보면, 간선이 많아지면 어떤 정점까지 도달하기 위한 최소 간선의 수만 해도 확률적으로 매우 적어지는 데다가, 가중치가 가능한 작은 쪽으로 선택해서 나가면 그보다도 훨씬 가까운 거리가 나올 가능성이 크다는 것이 명확합니다.
그래서 이를 저격하는 데이터는 매우 인위적으로 만들어야만 합니다.
int main()
{
int v = MAX_V;
int e = MAX_V - 1;
printf("%d %d\n", v, e);
for (int i = 1; i < v; i++)
printf("%d %d %d\n", i, i + 1, MAX_W);
}
small_inf_kill: wrong answer expected 99999000000, found -1, time: 0.091s
이미 방문한 정점을 다시 방문
정답 코드와 같이 구현을 하면 같은 정점이 우선순위 큐에 중복으로 삽입되는 일이 생길 수 있습니다. 우선순위 큐에서 뺀 적이 없는데도, 거리가 갱신되면 다시 삽입을 하기 때문입니다. 물론 이렇게 해도 우선순위 큐에는 최대 간선의 수만큼만 원소가 삽입되므로 시간복잡도에 문제는 없습니다.
중요한 것은 뺀 이후입니다. 정답 코드에서 다음 부분을 지우면 어떻게 될까요?
if (cur.weight > dist[cur.to])
continue;
얼핏 보면 이 코드가 없더라도, 만일 현재 정점을 이미 이전에 방문했다면 그 때의 거리가 더 짧았을 것이므로 다른 정점에 대해 거리를 갱신하지 못할 것이고, 그래서 별 문제가 없어 보입니다. 실제로 랜덤에 대해 테스트를 시켜봐도 정말 잘 돌아갑니다. 사실상 정답 코드와 거의 아무런 차이가 없는 것처럼 보입니다.
Testing duplicated.exe
random1: ok answer is 1711221, time: 0.225s
random2: ok answer is 1091541, time: 0.207s
random3: ok answer is 1793701, time: 0.320s
random4: ok answer is -1, time: 0.106s
random5: ok answer is 1485346, time: 0.324s
random6: ok answer is 1587244, time: 0.337s
random7: ok answer is 3857751, time: 0.253s
random8: ok answer is 2907308, time: 0.370s
random9: ok answer is 131426, time: 0.266s
random10: ok answer is 2855802, time: 0.374s
small_inf_kill: ok answer is 99999000000, time: 0.093s
하지만 이 코드를 집요하게 파고들면 저격이 가능합니다. 답을 틀리게 만드는 것은 아니고, 시간복잡도를 무너뜨려 시간 초과를 받게 할 수 있습니다.
이 코드가 비효율적이 되는 경우를 생각해봅시다. 이미 방문했던 정점을 다시 방문하는 것이 시간을 많이 걸리게 하려면 현재 정점에서 나가는 간선들에 대한 체크를 많이 하게 만들어야 합니다. 또한 같은 정점을 방문하는 횟수가 많아질수록 더 오래 걸립니다.
나가는 간선을 많게 하는 것은 그냥 한 정점에서 나가는 간선을 많이 추가하면 됩니다. 한 정점이 우선순위 큐에 많이 들어가게 하려면 어떻게 해야 할까요? 단순히 들어오는 간선이 많은 것으로는 충분하지 않습니다. 거리가 갱신될 때에만 다시 우선순위 큐에 추가하게 했기 때문입니다.
그래서 우리는 인위적으로 하나의 정점이 우선순위 큐에 아주 많이 추가되고, 여기에서 나가는 간선 역시 아주 많게 만들어 코드를 저격할 수 있습니다.
int main()
{
int v = MAX_V;
int e = (MAX_V - 3) * 2 + MAX_V - 1;
printf("%d %d\n", v, e);
for (int i = 2; i < v - 1; i++)
{
printf("%d %d %d\n", 1, i, MAX_W - i);
printf("%d %d %d\n", i, v - 1, i * 2);
}
for (int i = 1; i <= v; i++)
{
if (i == v - 1)
continue;
printf("%d %d %d\n", v - 1, i, MAX_W);
}
}
duplicated_kill: time limit exceeded, time: 24.155s
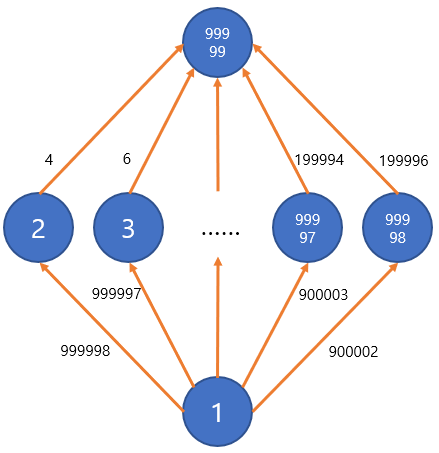
이 데이터를 첫 번째 for 루프까지 그림으로 표현하면 다음과 같습니다.
중복 방문하는 코드를 실행하면 우선 2~99998번 노드가 모두 우선순위 큐에 들어가고, 거리가 가장 작은 99998번부터 순서대로 우선순위 큐에서 나와 99999번 노드를 우선순위 큐에 넣게 됩니다. 99999번 노드로 가는 간선을 확인할 때마다 거리가 계속해서 줄어들기 때문에 99999번 노드는 우선순위 큐에 99997번이나 들어가게 됩니다!
여기에 두 번째 for 루프처럼 99999번 노드에서 자신을 제외한 모든 노드로 가는 간선들을 추가해주면, 99999번 노드는 99997번 우선순위 큐에서 나오고 그 때마다 99999개의 간선을 확인하게 됩니다. 시간복잡도를 멋지게 $O(V^2)$으로 만들어버린 것을 볼 수 있습니다.
2~99998번 정점에서 바로 100000번 정점으로 간선을 연결하지 않는 이유는 코드에 따라서는 우선순위 큐에서 뺀 순간 해당 정점이 목표 정점인지를 확인하고 리턴할 수도 있기 때문입니다.
이와 같은 실수는 의외로 굉장히 높은 비율로 다익스트라 알고리즘 코드에서 발견됩니다. 실수 정도가 아니라, 이것이 괜찮은 것으로 아는 사람들이 꽤 많습니다. 다익스트라 문제를 출제한다면 반드시 잡아야 할 코드입니다.
여담으로, 우선순위 큐를 구현하기에 따라서는 원소의 값을 변경하는 연산을 제공함으로써 우선순위 큐에 중복된 원소가 들어가는 것 자체를 막을 수도 있습니다. 이 경우에는 이러한 처리가 필요하지 않으며, 시간복잡도 역시 $O(VlogV + ElogV)$ 로 변하게 됩니다.
거꾸로 된 비교 연산자
이 경우는 데이터의 크기가 충분히 크면 랜덤으로도 웬만해서는 통과가 안 되지만 제한을 줄이면 잘 잡히지 않습니다. operator< 의 내부를 return weight < o.weight;로 바꾼 뒤, $V \le 500$이고 $E \le 1000$인 범위에서 데이터를 만들면 아래와 같은 결과가 나옵니다.
Testing reversed_comparator.exe
small1: ok answer is 1476310, time: 0.024s
small2: ok answer is -1, time: 0.021s
small3: ok answer is 235659, time: 0.022s
small4: ok answer is 3637501, time: 0.023s
small5: ok answer is 676724, time: 0.022s
small6: ok answer is 1476092, time: 0.025s
small7: ok answer is 982581, time: 0.022s
small8: ok answer is -1, time: 0.019s
small9: ok answer is 1205599, time: 0.017s
small10: ok answer is 47189, time: 0.020s
안타깝게도 비교 함수를 잘못 만들어도 오답이 나오지는 않습니다. 왜냐하면 중간에 각 정점이 최단 거리가 아닌 거리로 설정된 채로 진행하더라도 최단 거리까지 언젠가는 갱신이 반드시 되기 때문입니다. 하지만 시간 초과로 저격을 하는 것은 가능합니다.
만일 이 코드가 이전과 같이 $O(V^2)$이나 $O(VE)$ 등 다항식 시간 내에 들어오는 코드라면 깨뜨리기 어렵겠지만, 이 코드는 무려 지수복잡도를 가지는 코드입니다!… 만, 실제로는 최대 간선 가중치에 영향을 받기 때문에 데이터를 만드는 것이 쉽지는 않습니다.
우선 이 코드의 특성을 분석해보면 일단 거리가 가장 먼 것이 우선순위 큐에 들어가면 어딘가 종점에 도달할 때까지 계속해서 들어갈 것이 분명합니다. 이미 우선순위 큐 내에서 가장 거리가 먼 정점이었는데, 여기서 간선을 추가로 이용했다면 더 멀어지기 때문입니다. 어떻게 하면 금방 막히지 않고 갔던 길을 무수히 많이 반복하게 만들 수 있을까요? 어떤 정점에 계속해서 도달하게 하면서, 도달할 때마다 항상 거리가 줄어들게 만들면 됩니다.
아래 데이터의 원리를 간단히 설명하자면, 반드시 순서대로 방문해야 하는 정점들이 있고 각 정점의 사이에 길게 가는 길과 짧게 가는 길을 하나씩 추가하는데, 짧게 가는 길과 길게 가는 길의 길이 차이는 그 이후의 정점 전체를 최장으로 방문하는 것과 최단으로 방문하는 것의 차이보다 크게 만드는 것입니다. 그러면 마치 DFS로 완전 탐색을 하듯이 이미 방문했던 정점을 또 방문하고, 또 방문하고를 재귀적으로 반복하게 됩니다.
const int MAX_V = 500;
const int MAX_E = 1000;
const int MAX_W = 1000000;
#include <vector>
#include <string>
vector<string> edge;
int main()
{
srand((unsigned int)time(NULL));
int v = MAX_V;
int e = 0;
int i = v;
int cur = 1;
char buf[128];
while (true)
{
int need = cur / MAX_W + 2;
if (need >= i)
break;
int remainder = cur % MAX_W;
for (int j = 0; j < need - 2; j++)
{
sprintf(buf, "%d %d %d\n", i - need + j, i - need + j + 1, MAX_W);
edge.push_back(buf);
}
sprintf(buf, "%d %d %d\n", i - 2, i, MAX_W);
edge.push_back(buf);
sprintf(buf, "%d %d %d\n", i - need, i - 1, 1);
edge.push_back(buf);
sprintf(buf, "%d %d %d\n", i - 1, i, MAX_W - remainder - 1);
edge.push_back(buf);
i -= need;
cur <<= 1;
}
while (i > 1)
{
sprintf(buf, "%d %d %d\n", i - 1, i, MAX_W);
edge.push_back(buf);
i--;
}
e = edge.size();
printf("%d %d\n", v, e);
for (int i = 0; i < e; i++)
printf(edge[i].c_str());
}
reversed_comparator_kill: time limit exceeded, time: 21.007s
정점의 거리 대신 간선의 가중치를 우선순위 큐에 넣기
정답 코드에서 pq.push({ nxt.to, dist[nxt.to] }); 가 아니라 pq.push(nxt); 를 사용하는 경우입니다. 말도 안 되는 코드인 것 같지만 이것도 랜덤으로 쉽게 잡히지가 않습니다. 다행히도, 이런 코드에 대한 저격 데이터는 따로 만들지 않아도 됩니다. 위에서 만든 “이미 방문한 정점을 다시 방문”하는 코드를 저격한 데이터로도 공략이 됩니다.
원리를 생각해보면, 처음에 1번에서 2~99998번 정점으로 가는 간선이 모두 우선순위 큐에 들어가고, 99998번 정점으로 가는 간선의 가중치가 가장 작으므로 99998번 정점에서 99999번 정점으로 가는 간선이 우선순위 큐에 추가되는데, 이 간선의 가중치가 가장 작기 때문에 99999번 정점에서 나가는 간선 99999개를 곧바로 모두 확인하게 됩니다.. 그 다음은 99997번 정점이 나오고, 다시 99999번 정점이 들어가고, 나가는 간선 99999개를 다시 보고… 이를 반복하면 $O(V^2)$ 이 됩니다.
Testing edge_pq.exe
random1: ok answer is 1711221, time: 0.264s
random2: ok answer is 1091541, time: 0.246s
random3: ok answer is 1793701, time: 0.444s
random4: ok answer is -1, time: 0.131s
random5: ok answer is 1485346, time: 0.386s
random6: ok answer is 1587244, time: 0.428s
random7: ok answer is 3857751, time: 0.369s
random8: ok answer is 2907308, time: 0.464s
random9: ok answer is 131426, time: 0.264s
random10: ok answer is 2855802, time: 0.536s
small_inf_kill: ok answer is 99999000000, time: 0.094s
duplicated_kill: time limit exceeded, time: 23.030s
reversed_comparator_kill: ok answer is 202564545, time: 0.019s
간선의 가중치를 우선순위 큐에 넣을 뿐 아니라, 비교 연산자도 틀리기(…)
그런데 정말 억울하기 짝이 없게도, 이 두 가지 실수를 동시에 한 코드는 또 잡히지가 않습니다. 한숨이 나오지만, 절대로 통과되어서는 안 되는 이 코드도 잡아봅시다. 이전 데이터를 조금만 변형하면 됩니다.
int main()
{
int v = MAX_V;
int e = (MAX_V - 3) * 2 + MAX_V - 1;
printf("%d %d\n", v, e);
for (int i = 2; i < v - 1; i++)
{
printf("%d %d %d\n", 1, i, i);
printf("%d %d %d\n", i, v - 1, i);
}
for (int i = 1; i <= v; i++)
{
if (i == v - 1)
continue;
printf("%d %d %d\n", v - 1, i, 1);
}
}
Testing reversed_edge_pq.exe
random1: ok answer is 1711221, time: 0.365s
random2: ok answer is 1091541, time: 0.312s
random3: ok answer is 1793701, time: 0.730s
random4: ok answer is -1, time: 0.143s
random5: ok answer is 1485346, time: 0.629s
random6: ok answer is 1587244, time: 0.755s
random7: ok answer is 3857751, time: 0.586s
random8: ok answer is 2907308, time: 0.890s
random9: ok answer is 131426, time: 0.337s
random10: ok answer is 2855802, time: 0.782s
small_inf_kill: ok answer is 99999000000, time: 0.097s
duplicated_kill: ok answer is 2000002, time: 0.242s
reversed_comparator_kill: ok answer is 202564545, time: 0.056s
reversed_edge_pq_kill: runtime error; exit code is -1073740791, time: 16.668s
간선의 가중치를 1->i와 i->99999가 모두 i가 되도록 했기 때문에, 더 큰 정점이 먼저 나와 99999를 우선순위 큐에 넣고 진행하게 됩니다. 재미있는 것은 99999번 정점에서 나머지 정점으로의 간선의 가중치를 1로 했다는 점인데, 이 때문에 이 간선들은 다른 간선들이 모두 우선순위 큐에서 나오기 전까지 빠져나오지 않고 쌓이게 됩니다. 그래서 우선순위 큐에 총 $O(V^2)$개의 간선이 들어가게 되어 시간복잡도가 $O(V^2logV)$가 될 뿐 아니라 공간복잡도도 $O(V^2)$이 되어 우선순위 큐가 너무 커짐으로 인해 메모리 제한에도 금방 걸리게 됩니다.
SPFA 알고리즘
이 부분은 이 글에서 자세히 다루지는 않지만 다익스트라 문제를 낼 때 고려해야 하는 것 중 하나입니다. SPFA (Shortest Path Faster Algorithm)은 최악의 경우 $O(VE)$ 시간에 동작하는 알고리즘으로 음수 간선이 있는 경우에도 사용할 수 있어 벨만-포드 알고리즘과 유사하지만 평균적으로 $O(E)$ 시간에 동작하므로 이러한 풀이가 통과되는 것을 원하지 않는다면 적절한 데이터를 추가하여 최악의 케이스를 만들어줘야 합니다.
기존 정답 코드에서 우선순위 큐 대신 그냥 큐를 사용하는 것도 이와 비슷한 풀이입니다.
결론
데이터를 만드는 것은 어렵고, 특히 대회 문제를 준비한다면 가능성이 있는 모든 오류 코드를 잡아내기 위한 강력한 데이터를 준비하는 데에는 많은 시간이 필요합니다. 다익스트라 알고리즘과 같이 매우 기본적인 알고리즘에 속하는 것도 이렇게 다양한 실수가 나올 수 있고 인위적인 데이터가 아니고서는 잡기 어렵다는 것을 보았습니다.
데이터를 잘 만드는 것은 비단 이런 문제에서만 신경써야 하는 것이 아니라, 어떤 문제를 만들더라도 어떤 실수나 잘못된 풀이가 다양하게 나올 수 있는지 생각해보고 그 풀이들이 현재 데이터를 통과하지 않는지 철저하게 확인해야 합니다.