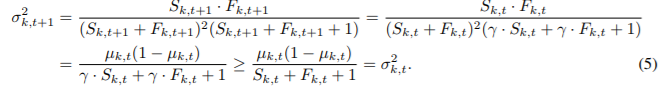Thompson Sampling 소개 및 non-stationary MAB 문제 해결
이번 포스트에서는 Multi Armed Bandit 문제와 Thompson sampling을 소개하고 non-stationary MAB를 해결하는 간단한 알고리즘 중 하나인 Discounted Thompson Sampling에 대해 알아보려고 합니다. 이 알고리즘은 Vishnu Raj, Sheetal Kalyani의 논문 Taming Non-stationary Bandits: A Bayesian Approach에 자세히 소개되어 있습니다. 이 논문에서는 또 하나의 알고리즘 Discounted Optimistic Thompson Sampling(dOTS)을 제안했지만 본 포스트에서는 다루지 않겠습니다.
Multi Armed Bandit, Thompson sampling에 대한 소개글은 Daniel Russo, Benjamin Van Roy, Abbas Kazerouni, Ian Osband, Zheng Wen의 A Tutorial on Thompson Sampling을 참고하여 작성하였습니다.
Multi Armed Bandit Problem
Multi Armed Bandit(MAB) 문제는 통계학, 컴퓨터 과학, 경제학 등 많은 분야에서 수십년 동안 집중적으로 연구되어 왔습니다. one-armed bandit(직역하면 외팔이 강도)은 도박꾼의 돈을 털어버리는 슬롯 머신의 모습을 빗댄 고전 용어입니다. 이름에서 유추할 수 있듯이 MAB 문제의 이름은 도박꾼이 카지노에서 여러 슬롯 머신의 arm을 당기는 모습에서 착안되어 붙여졌습니다.
한 도박꾼이 카지노에 들어가서 슬롯 머신을 돌려서 최대한 많은 돈을 벌고자 합니다. 카지노에는 많은 슬롯 머신이 있고 각각의 슬롯 머신은 한 번 arm을 당길 때마다 알려지지 않은 특정 분포에 따라 돈을 내놓습니다. 이에 따라 도박꾼은 실험적으로 슬롯 머신을 몇 번 돌려서 해당 슬롯 머신의 패턴을 파악한 뒤에 얻은 정보를 바탕으로 최대 수익을 얻으려고 노력하게 될 것입니다. 여기서 도박꾼은 한 가지 딜레마에 직면하게 됩니다. 기존에 갖고 있던 정보를 토대로 가장 좋은 arm을 선택(exploitation)하면 실험에 필요한 돈을 절약하게 되지만 정보가 부족하기 때문에 최종 수익이 높을 것이라고 장담하지 못합니다. 그렇다고 너무 많은 실험(exploration)을 하면 슬롯 머신에 대해 정확한 정보를 얻을 수 있지만 많은 지출이 발생하게 됩니다. 이러한 trade-off 관계를 잘 고려하여 최대 이익을 얻는 전략을 찾는 것이 바로 MAB 문제의 핵심입니다.
구체적으로 다음과 같은 MAB의 한 문제를 살펴 봅시다.
(Bernoulli Bandit) K개의 arm이 존재하고 각각의 arm은 당겼을 때 success나 failure 둘 중 하나를 발생시킨다. arm $k \in {1, …, K}$는 $\theta_k \in [0, 1]$ 확률로 success를 발생시킨다. success 확률 $(\theta_1, …, \theta_K)$ 는 agent에게 알려져 있지 않다. 하지만, 시간이 지나면서 agent는 arm에 따른 결과를 관찰할 것이고 이를 통해 success 확률을 학습할 수 있을 것이다. 목표는 주어진 기간 $T$ 동안 success의 누적 총계를 최대화하는 것이다. $T$는 arm 개수 $K$에 비해 크게 주어진다.
이러한 형태의 MAB 문제는 현실에서 자주 등장합니다. 예를 들어서, 웹사이트에서 배너 광고를 띄우는 상황을 가정해봅시다. 하루동안 혹은 한 번의 사이트 방문에서 게시되는 광고의 수는 정해져 있기 때문에 적절한 기준을 통해 매번 게시할 광고를 선택해 주어야 합니다. 광고를 게시하는 행위를 arm을 당기는 것이라고 합시다. 그러면 게시된 광고를 유저가 클릭했을 경우 success, 클릭하지 않고 사이트를 떠나는 경우 failure가 발생했다고 할 수 있습니다. 마지막으로 각 광고에 대해 알려져 있지 않은 success 확률이 있다고 가정할 수 있습니다. 웹사이트 운영자는 특정 기간동안 사이트의 방문자가 광고를 최대한 많이 클릭하도록 전략을 찾을 것이고 이는 곧 bernoulli bandit 문제를 푸는 것과 같게 됩니다.
Thompson Sampling for the Bernoulli Bandit
Thompson Sampling은 최근에 MAB 문제를 해결하는 데 있어 좋은 성능을 내고 있는 알고리즘으로 알려져 있습니다. Thompson Sampling은 각 reward 분포의 파라매터를 확률 변수로 보고 이 파라매터의 분포로부터 무작위로 추출하여 해당 값에 대한 reward 기댓값이 가장 높은 arm을 선택합니다. 그리고 나서 bayesian 정리를 이용하여 선택한 arm에 대한 파라매터의 분포를 업데이트합니다. 이 과정을 반복하면서 reward의 분포을 학습하게 되고 점점 높은 reward 평균의 arm을 자주 선택하게 됩니다. 이 글에서는 특별히 Bernoulli bandits에 대한 Thompson Sampling을 살펴 봅니다.
위의 Bernoulli Bandit 문제에서 success가 발생하면 reward 1을 얻고 failure가 발생하면 아무 reward를 받지 않는다고 합시다. 다시 말해, arm $k$를 당기면 $\theta_k$의 확률로 reward 1을 받고 $1-\theta_k$의 확률로 reward를 받지 못 합니다. 처음에 agent는 arm $x_1$을 당기고 $r_1$의 reward를 받습니다. agent는 이 결과 $r_1$을 보고 arm $x_2$를 당긴 뒤에 $r_2$의 reward를 얻게 됩니다. agent는 계속해서 이러한 과정을 반복할 것입니다. 여기에서 agent가 사전에 각 $\theta_k$에 대한 분포를 독립된 beta 분포로 추정했다고 합시다. 그러면 추정값 $\hat{\theta}_k$~$Beta(\alpha_k,\beta_k)$라고 할 수 있고 $\hat{\theta}_k$에 대한 prior probability density function은 다음과 같게 됩니다.
이제 arm $x_t$를 시행했다고 합시다. beta 분포의 conjugacy 특성 때문에 reward $r$을 관찰한 뒤의 $\alpha_k, \beta_k$는 다음과 같이 업데이트됩니다.
\[(\alpha_k,\beta_k) \leftarrow \begin{cases} (\alpha_k,\beta_k) & \text{if } x_t \neq k \\ (\alpha_k + r,\beta_k+1-r) & \text{if } x_t = k \end{cases}\]초기의 $\alpha,\beta$는 상황에 맞게 설정합니다. 일반적으로 $\theta$에 대한 아무런 정보를 가지지 않았다면 $(\alpha, \beta) = (1, 1)$에서 시작합니다. 이 때의 beta 분포는 uniform 분포가 됩니다. 시각 $t$일 때, Thompson Sampling은 각 arm $k$에 대해 추정값 $\hat{\theta_k}$을 posterior 분포인 $Beta(\alpha_k,\beta_k)$로부터 뽑습니다. 이 중에서 가장 큰 추정값에 대한 arm $x_t$를 수행하고 관찰된 reward $r_t$에 따라 앞에서 설명한 바와 같이 해당 파래매터 $\alpha_{x_t}, \beta_{x_t}$를 업데이트합니다.
다음은 Bernoulli Bandit에 대한 Thompson Sampling의 의사 코드입니다.
파라매터가 ($\alpha$,$\beta$)인 beta 분포는 평균이 $\alpha \over (\alpha+\beta)$이고 분산이 $\alpha \beta \over {(\alpha+\beta)^2(\alpha+\beta+1)}$입니다. 평균이 같을 때 $\alpha+\beta$가 증가하면 분산이 작아지기 때문에 분포 모양이 평균을 중심으로 뾰족해지는 특성이 있습니다. 관찰한 reward가 많아질수록 arm에 대한 분포는 점점 뾰족해지는 양상을 띄며 각 arm에 대한 추정값이 점점 해당 분포의 평균에 가까운 경우가 많아집니다. 따라서 시간이 흐를수록 평균 reward가 낮은 arm은 선택될 가능성이 낮아지고 평균 reward가 높은 arm이 많이 선택됩니다.
아래 왼쪽 그래프는 파라매터가 각각 $(\alpha_1,\beta_1)=(601,401),(\alpha_2,\beta_2)=(401,601),(\alpha_3,\beta_3)=(2,3)$인 beta 분포를 나타냅니다. 그리고 오른쪽 그래프는 평균 reward가 각각 $\theta_1=0.9, \theta_2=0.8, \theta_3=0.7$일 때 시간의 흐름에 따라 각 arm이 선택되는 정도를 보여줍니다.
Nonstationary Systems
지금까지 우리가 고려한 문제에서는 모델 파라메터 $\theta$를 시간의 변화와 상관이 없는 상수로 가정했습니다. 하지만, 많은 현실적인 문제에서 이러한 파라메터는 시간의 흐름에 따라 변하는 경우가 많습니다. 위에서 들었던 광고를 예시로 들면, 한 광고에 대한 방문자의 선호도는 제품에 대한 소문, 잦은 광고 노출에 따른 흥미 상실 등 여러가지 이유로 변할 수 있기 때문입니다. 이러한 환경에서의 MAB 문제를 non-stationary MAB 문제라고 부릅니다. 앞에서 소개한 BernTS는 시간의 흐름에 따라 파라매터 $\alpha+\beta$ 값이 계속해서 증가하므로 변하는 $\theta$에 대한 추정을 하기 점점 어려워집니다. 이제 이러한 문제를 해결하는 간단한 방법 중 하나인 Discounted Thompson Sampling을 소개합니다.
Discounted Thompson Sampling
이 알고리즘의 핵심 아이디어는 과거에 관찰한 reward에 대해 discount를 해서 시간에 따라 변하는 $\theta$를 추적하는 것입니다. discount는 현재로부터 지나간 단위 시간만큼 해당 날에 관찰한 reward에 $\gamma \in (0,1]$를 곱해서 적용합니다. 즉, 현재 시각으로부터 $m$일 전의 reward $r$은 현재에 $r*\gamma^m$만큼 기여를 하게 됩니다. 이 아이디어를 BernTS에 적용하면 다음과 같이 Discounted Thompson Sampling 알고리즘이 됩니다.
선택되지 않은 arm에 대한 파라매터 $\theta$의 추정값 분포의 평균과 분산을 살펴 봅시다. 초기값 $\alpha_0, \beta_0$의 영향을 무시하면 시간의 변화에 따른 평균과 분산은 다음과 같은 관계를 가집니다.
discount에 의해 평균은 변하지 않고 분산은 증가함을 알 수 있습니다. 분산이 증가한다는 것은 덜 explorer된 arm이 discount에 의해 앞으로 선택될 가능성이 증가함을 의미합니다. 이러한 성질을 바탕으로 dTS는 시간에 따라 변하는 $\theta$를 추척할 수 있게 됩니다.
Performance
$X_{k,t}$를 $t$번째 시각에 $k$번째 arm을 당겼을 때 얻은 reward라고 합시다. $X_{k,t}$는 평균이 $\mu_{k,t}=\mathbb{E}[X_{k,t}]$인 Bernoulli 분포의 확률 변수입니다. $t$번째 시각에 최대 reward 기댓값을 $\mu_t^*=\max{\mu_{k,t}:k\in \mathcal{K}}$라고 합시다. 그러면 regret은 다음과 같이 정의됩니다. 이 값이 작을수록 좋은 성능의 알고리즘입니다.
\(\mathcal{R}^{\pi}(T)=\sum_{k=1}^T \mu_t^* - \mathbb{E}_{\pi,\mu}\left[\sum_{k=1}^T X_{I_t^\pi,t}\right]\) <Taming Non-stationary Bandits: A Bayesian Approach>에서는 다음 세 가지의 환경에서 dTS의 performance를 측정했습니다.
- Slow Varying Environment: 느리게 변하는 환경입니다. 각 arm의 success 확률은 시간에 대한 0과 1사이의 sinusoidal 함수입니다. 환경이 변화를 느리게 하기 위해서 모든 sinusoidal 함수의 주기를 1000 단위 시간으로 설정했습니다. 각 arm의 success 확률을 다르게 하기 위해서 sinusoidal의 offset을 $0, {\pi \over 2}, \pi, {3 \pi \over 2}$로 설정했습니다.
- Fast Varying Environment: 빠르게 변하는 환경입니다. 위 환경에서 sinusoidal 함수의 주기를 100 단위 시간으로 설정했습니다.
- Abruptly Varying Environment: 갑작스럽게 변하는 환경입니다. success 확률에 매 주기마다 한 번 큰 변화가 일어납니다. 4개의 arm 모두 확률 $p=0$에서 시작하여 arm1은 $t=50$에 $p=0.10$, arm2은 $t=100$에 $p=0.37$, arm3은 $t=150$에 $p=0.63$, arm4은 $t=200$에 $p=0.90$로 변합니다. 모든 arm은 $t=250$에 $p=0$으로 감소하고 이러한 변화를 반복합니다.
다음은 여러 알고리즘과 dTS의 performance를 비교한 그래프입니다.
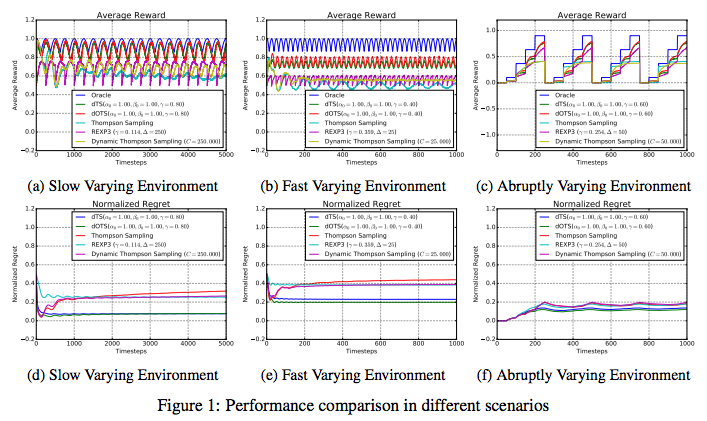
dTS는 환경의 변화에 잘 맞춰 regret을 감소시키는 것을 볼 수 있습니다. 특히 일반 Thompson Sampling에 비해 좋은 성능을 내고 있음을 알 수 있습니다.