현대 암호 1 : 블록 암호
저번 포스팅에서는 고전 암호를 다루었습니다. 이번 포스팅에서는 현대 암호 중에서도 DES, AES와 같은 블록 암호를 다루도록 하겠습니다.
블록 암호란?
블록 암호(Block Cipher)란 평문을 블록 단위로 암호화하는 대칭키 암호 시스템입니다. 대칭키 암호 시스템은 암호화와 복호화를 할 때 동일한 키가 사용되는 암호 시스템입니다. 반대로 암호화와 복호화를 할 때 동일하지 않은 키가 사용되지 않는 공개키 암호 시스템도 존재하는데, 공개키 암호 시스템 보다는 대칭키 암호 시스템이 우리의 직관과 조금 더 맞는 시스템일 것입니다. 참고로 저번 포스팅에서 다룬 고전 암호는 전부 대칭키 암호 시스템입니다. 예를 들어 비제네르 암호에서 암호화를 할 때도 키 ENCRYPT를, 복호화를 할 때도 키 ENCRYPT를 사용했습니다.
블록 단위로 암호화를 한다는 의미는 암호화 방식을 정할 때 임의의 길이의 평문에 대해 고민할 필요가 없이 고정된 길이의 각 블록을 암호화하는 방식만 정하면 됩니다. 대표적인 블록 암호로는 DES, AES가 있고 DES는 블록의 크기가 64비트, AES는 128/192/256비트입니다.
패딩
주어진 평문을 블록 암호로 암호화하기 위해서는 평문을 우선 블록 크기의 배수로 만들어야 합니다. 예를 들어 DES로 암호화를 한다면 평문은 $64 \times n$비트이어야 할 것입니다. 평문의 길이가 블록 크기의 배수가 아닌 경우, 블록 크기의 배수가 되게끔 패딩을 추가합니다. 이러한 패딩을 하는 알고리즘은 PKCS#5, ANSIX923 등이 존재하는데, 그다지 어려운 내용이 아니니 직접 찾아보세요.
패딩의 가장 중요한 원칙은 $P(M)$ 으로부터 $M$을 복구할 수 있어야 한다는 점입니다. 이 원칙이 지켜지지 않으면 패딩된 메시지로부터 원본 메시지를 찾을 수 없습니다. 예를 들어 평문의 길이를 32비트의 배수로 만들고 싶을 때 모자란 만큼 0으로 채워 32의 배수로 만드는 패딩을 생각해봅시다. 그러면 패딩된 메시지 00010011 01000111 11001000 00000000에서 실제 평문이 어디까지인지 알 수 있을까요? 00010011 01000111 11001000 00000000일 수도 있고, 00010011 01000111 11001000 00000000일 수도 있고, 00010011 01000111 11001000 00000000일 수도 있습니다. 즉 비트 단위의 All zero 패딩은 패딩된 메시지로부터 원본 메시지를 복구할 수 없으므로 사용할 수 없는 패딩입니다.
블록 암호의 운용 방식
패딩을 통해 주어진 평문을 블록 크기의 배수로 만드는데 성공했습니다. 그 다음으로 어떻게 평문을 암호화할지 정해봅시다. 가장 쉽게 떠올릴 수 있는 방법은 그냥 평문을 블록 크기대로 잘라 독립적으로 암호화를 하는 방식일 것입니다. 이러한 방식을 ECB 모드라고 합니다. 하지만 각 블록을 독립적으로 암호화를 하는 방식은 간단하고 병렬 처리를 할 수 있다는 장점이 있지만, 보안의 관점에서 볼 때 다소 취약한 부분도 있기 때문에 CBC 모드, CTR 모드등의 다양한 방식이 있습니다.
ECB 모드
ECB 모드는 앞서 언급했듯 각 블록을 독립적으로 암호화하는 방법입니다. 편의상 블록의 크기를 4글자라고 할 때, 16글자의 평문을 ECB 모드에서 16글자의 암호문으로 암호화하는 과정은 아래와 같습니다.
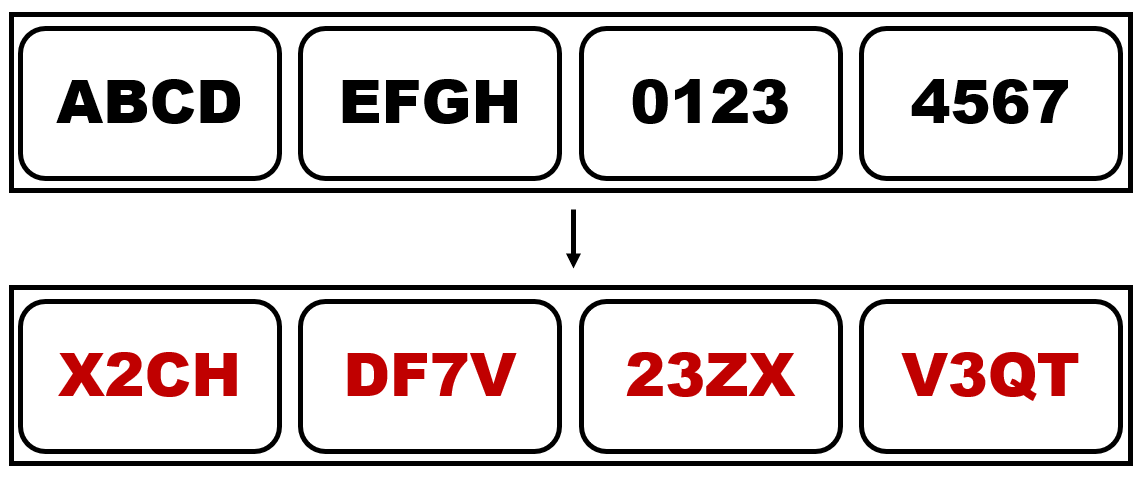
ECB 모드는 간단하고 병렬 처리를 할 수 있다는 장점이 있지만, 굉장히 중요한 보안 상의 취약점이 있습니다. 그 취약점은 키가 고정되어있을 경우 평문 내에서 동일한 블록들은 암호화한 결과 또한 동일하다 입니다. 이를 통해 암호문을 통해 평문의 내용에 대한 정보를 일부 습득할 수 있습니다. 대다수의 파일에서는 이 취약점이 큰 의미가 없지만, bmp 파일에서는 이 취약점으로 인해 그림의 윤곽이 드러날 수 있게 됩니다. bmp 파일 형식은 그림 픽셀의 RGB값을 압축과 손실 없이 그대로 저장하는 그림 파일 형식으로, 그림파일 내에서 배경은 보통 동일한 색인 경우가 많으므로 블록의 크기가 잘 맞아떨어진다면 배경과 피사체를 구분할 수 있게 되는 것입니다.
실제로 2015 국가암호공모전 06번 문제에서 이와 관련한 취약점으로 풀이를 하는 문제가 출제된 적 있습니다. 문제 링크

첨부파일에는 암호화/복호화를 수행하는 프로그램과 암호화된 파일이 들어있습니다.
주어진 프로그램을 리버싱해 문제를 해결할 수도 있지만, 이 대회에서 의도한 풀이는 아닐 것입니다. 대신 다양한 파일을 대상으로 실험을 해보면 이 프로그램으로 암호화된 파일의 구조를 파악할 수 있고, 16비트 단위로 ECB모드 암호화를 수행한 후 bit rotation을 추가로 수행함을 알 수 있습니다. 그러므로 bit rotation을 되돌리고 나면 ECB모드로 암호화된 그림 파일을 얻을 수 있고, 이를 bmp 파일의 헤더와 잘 조합해보면 아래와 같이 그림파일의 대략적인 윤곽을 밝혀낼 수 있습니다.

이 취약점은 키를 모르는 상황에서 암호문을 이용해 유효한 평문을 만들어낼 때에도 사용할 수 있습니다. 예를 들어 A 게임회사에서 회원들에게 설날을 맞아 랜덤한 게임캐쉬가 든 쿠폰을 발급했다고 합시다. 이 쿠폰은 1000P Coupon, 4752P Coupon, 95162P Coupon 등의 평문을 각 회원에게 할당된 임의의 키로 암호화한 암호문이라고 해봅시다. 사용자는 이 쿠폰의 일련번호를 게임 클라이언트 내에서 입력하고, 서버는 미리 가지고 있던 키로 해당 일련번호를 복호화해 캐쉬를 지급합니다. 사용자 blisstoner가
1000P Coupon을 받았다고 가정해봅시다. 만약 블록의 크기가 4글자인 암호를 이용해 ECB 모드로 쿠폰을 생성했다면 어떤 취약점이 발생할까요? 쿠폰은 아래와 같이 생겼을 것입니다.
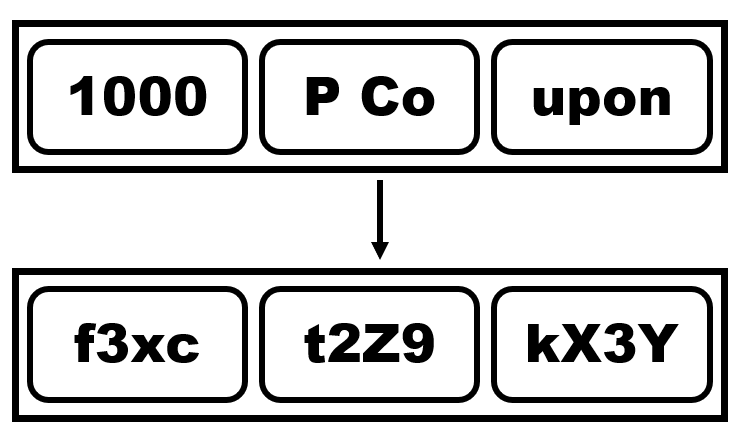
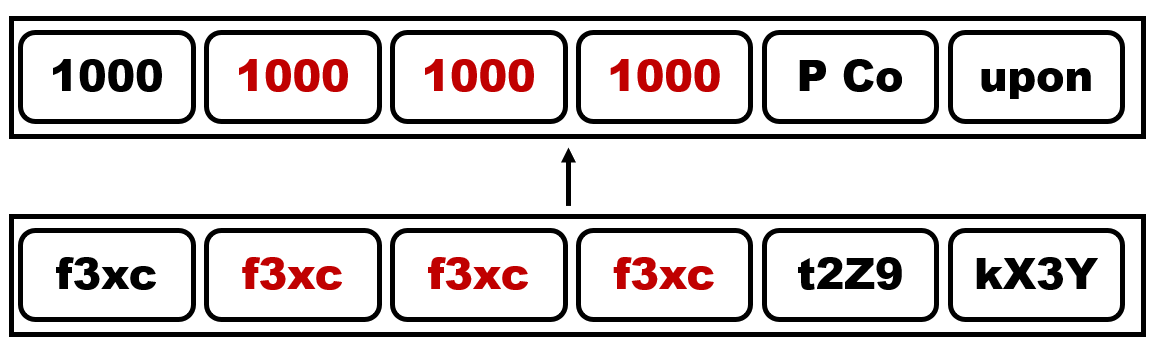
사용자 blisstoner는 f3xct2Z9kX3Y라는 일련번호를 얻었고, 이 일련번호를 입력해서 1000P를 얻을 수 있을 것입니다. 그런데 blisstoner가 일련번호를 f3xcf3xcf3xcf3xct2Z9kX3Y로 변형했다고 해봅시다. 이런 간단한 조작으로 인해 1000P Coupon은 1000100010001000P Coupon이 되었습니다. 이러한 공격을 Replay Attack이라고 합니다.
너무 작위적인 상황이 아닌가 싶을수도 있지만, 2013년에도 ECB 모드의 취약점으로 인해 보안이 취약해지는 사건이 발생한 적이 있습니다. 2013년, Adobe에서 3800만명 가량의 개인정보가 유출되었습니다. 이 유출 자체가 ECB 모드의 취약점으로 발생한 것은 아닙니다. 그러나 패스워드가 3DES ECB 모드로 salt 없이 모두 동일한 키로 암호화되어 있었기 때문에 암호화된 결과가 동일한 패스워드끼리 그룹을 만들어 비밀번호 찾기의 힌트를 가지고 비밀번호를 매우 간단하게 역추적할 수 있게 되었습니다. 링크
이렇듯 ECB 모드는 취약한 점이 많기 때문에 사용하지 않는 것을 권장합니다.
CBC 모드
CBC 모드는 앞서 언급했듯 현재 블록을 암호화할 때 이전 블록의 암호화 결과를 XOR한 후에 암호화 하는 방법입니다.이전 블록의 암호화 결과가 계속 사용됨에 따라 각 암호문 블록은 현재 평문 블록 뿐 아니라 이전의 모든 평문 블록에 영향을 받습니다. CBC 모드에서 암호화하는 과정은 아래와 같습니다.
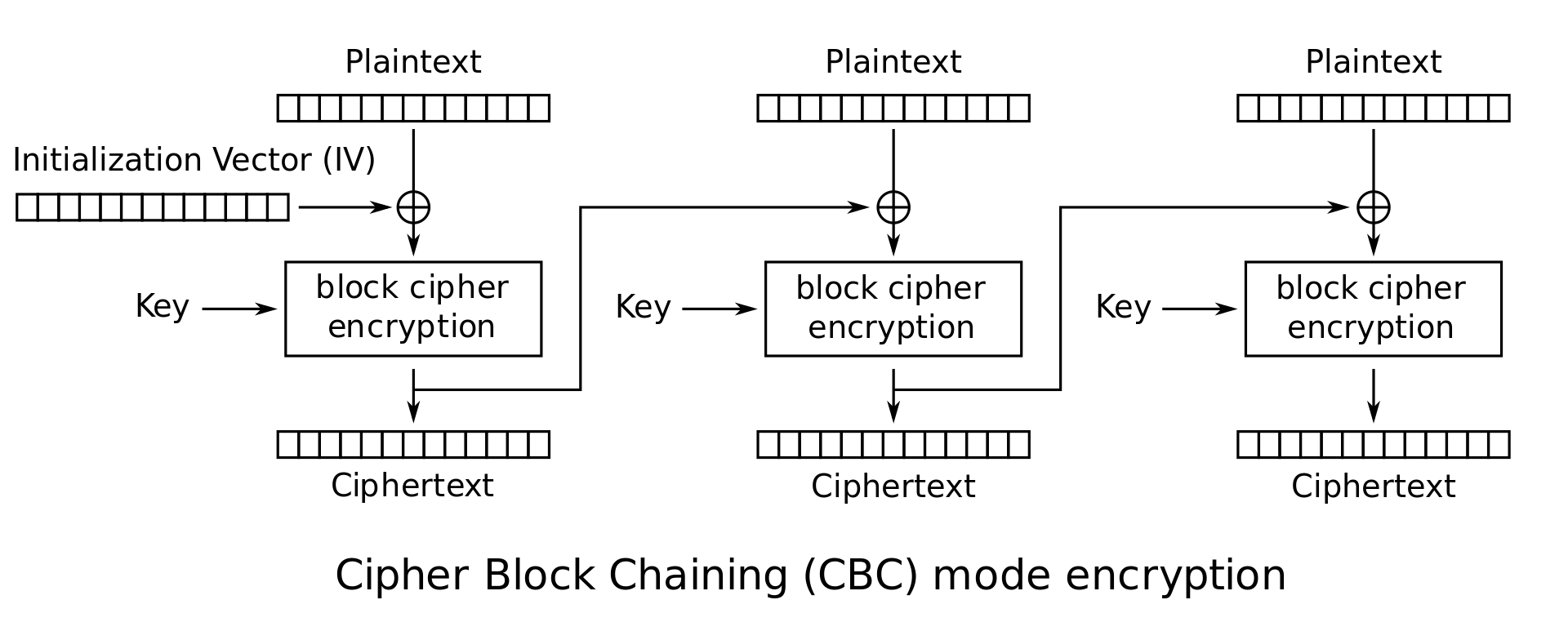
Initialization Vector, IV라고 하는 것은 동일한 평문을 동일한 키에서 암호화하더라도 매번 다른 결과를 내도록 하기 위해 사용하는 것으로, 특히 CBC 모드에서는 첫 번째 블록에 XOR하는 용도로 사용됩니다. IV는 암호를 복호화할 사람에게 미리 제공되어야 하고 키와 달리 공개되어도 상관없습니다. 미리 송신자와 수신자 간에 IV를 어떤 것으로 사용할지 정해두거나 파일에 IV를 기록해두는 방식으로 IV를 공유합니다.
CBC 모드에서는 암호화 과정을 병렬적으로 수행할 수 없습니다. $n$번째 블록을 암호화하기 위해서는 $n-1$번째 블록을 암호화한 결과가 필요하고, $n-1$번째 블록을 암호화한 결과를 알기 위해서는 곧 $n-2$번째 블록을 암호화한 결과를 알아야하기 때문에 이전의 모든 블록의 암호화가 끝나야 $n$번째 블록의 암호화를 진행할 수 있습니다. 단, 복호화 과정에서는 일단 병렬적으로 복호화를 수행한 뒤 XOR만 앞에서부터 차례대로 하면 되므로 복호화 과정은 병렬적으로 수행할 수 있습니다.
CBC 모드는 ECB 모드와 다르게 블록의 내용이 동일하더라도 이전 블록의 암호화 결과가 대다수의 경우 다르므로 암호화된 결과가 다릅니다. 그러므로 앞의 ECB 모드로 암호화된 쿠폰에서 쓰였던 Replay Attack이 불가능합니다. 그러나 암호문 혹은 IV의 비트를 조작해 특정 블록의 비트를 변경하는 공격이 새롭게 가능해집니다. 이러한 공격은 CBC Bit-flipping Attack이라고 불립니다. ECB 모드와 비슷하게 쿠폰을 가지고 암호화 과정을 다시 살펴봅시다.
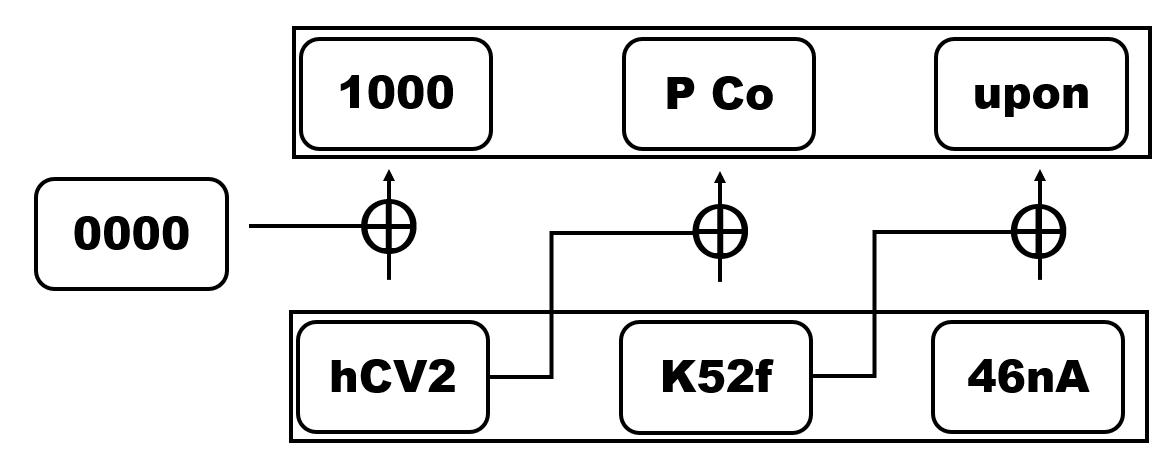
이 쿠폰을 활성화시키기 위해서는 IV 0000과 일련번호 hCV2K52f46nA를 입력해야 합니다. 이전과 달리 hCV2를 여러 번 쓴다고 해서 쿠폰의 내용이 100010001000P Coupon으로 바뀌지 않습니다. 그러나 IV의 LSB를 뒤집어 0000에서 0001로 만들면 어떻게 될까요? 복호화 과정을 생각해보면 우선 hCV2를 복호화한 뒤 IV를 XOR하므로 평문의 LSB 또한 0에서 1로 바뀌게 됩니다.
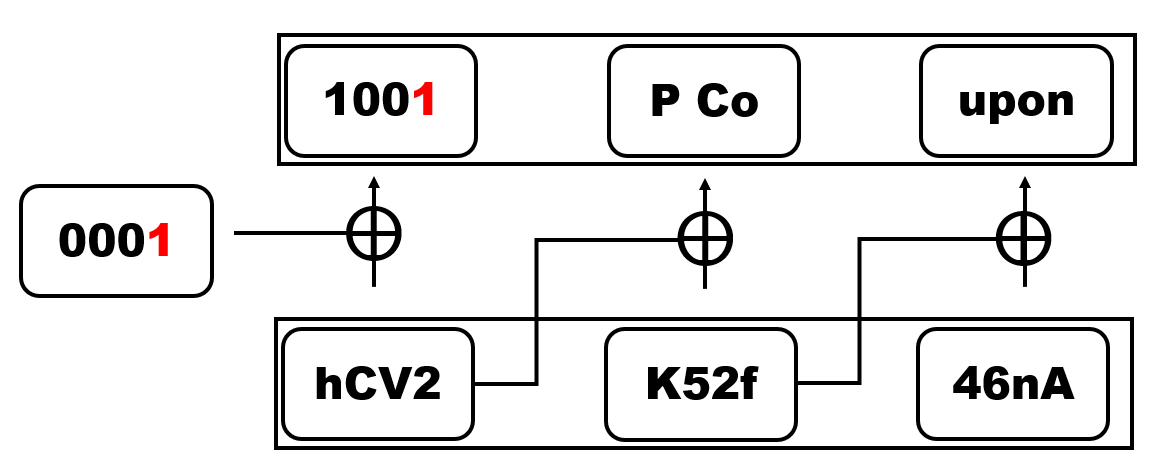
이와 같이 Bit flip을 통해 평문의 일부 Bit를 변형할 수 있습니다. 그 Bit이 admin 여부를 체크하는 비트라던가, 잔고의 양을 나타내는 비트라던가 할 경우 굉장히 큰 보안상의 취약점을 야기할 수 있습니다. 2017 GoN Recruit Crypto CBC문제에서 이를 이용한 문제가 나온 적 있습니다. Write-up 이 취약점은 CTF에 간간히 잘 나오는 취약점입니다.
CTR 모드
마지막으로 소개할 CTR 모드는 평문을 암호화하기 위해 블록 자체를 암호화하는 대신, 해당 암호화 과정에서 사용할 nonce와 블록당 1씩 증가할 counter를 두어 nonce+counter를 암호화한 후 블록에 XOR을 함으로서 암호화하는 방식입니다.
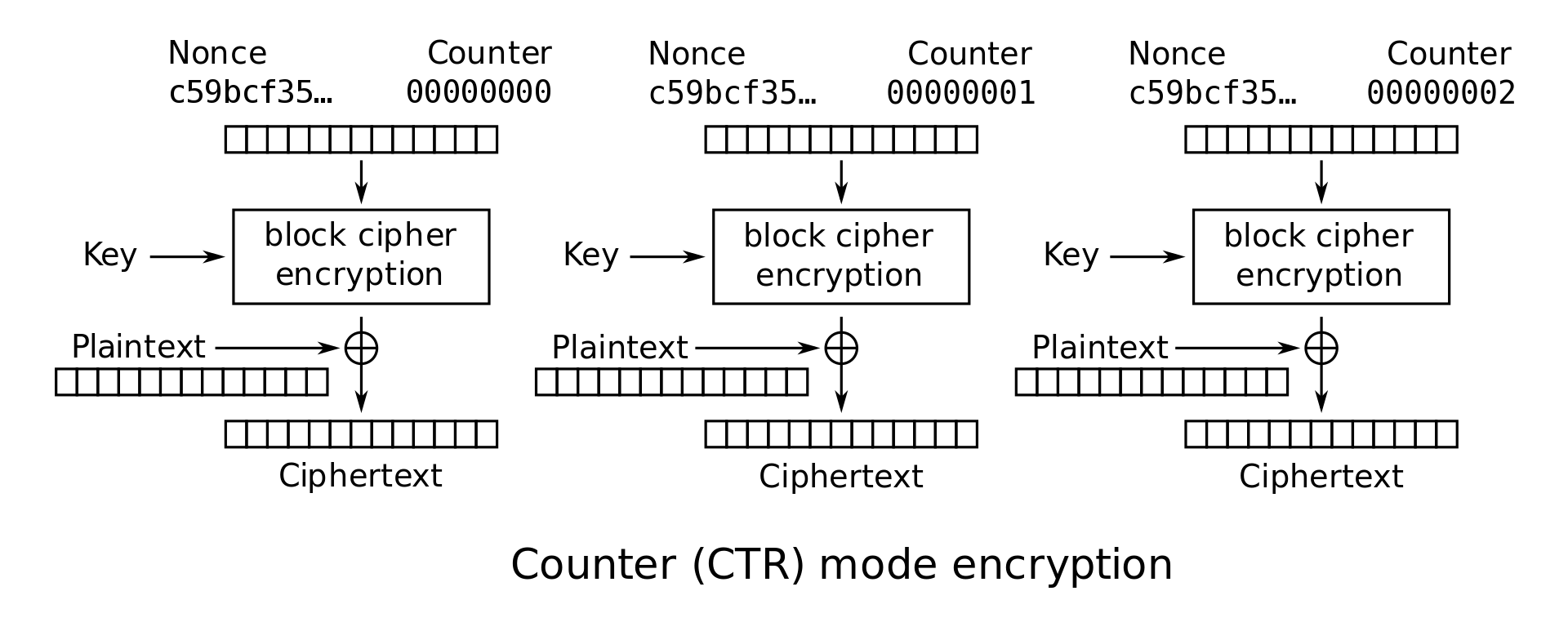
CTR 모드는 우선 CBC 모드와 비슷하게 다른 위치에 있는 두 블록의 내용이 동일하더라도 counter 값이 다르므로 암호화된 결과가 다르고, 동일한 암호화와 복호화가 모두 같은 구조를 가지고 있어 암호화 함수와 복호화 함수를 다르게 둘 필요가 없다는 장점을 가지고 있습니다. 또한 각 블록의 암호화/복호화 과정은 다른 블록의 영향을 받지 않으므로 병렬로 처리를 할 수 있다는 장점도 있습니다. 그러나 CBC 모드와 같이 Bit-flipping Attack에는 취약합니다.
이번에 소개한 ECB, CBC, CTR 모드 이외에도 CFB, OFB 모드 등이 존재하나 이들은 CBC, CTR 모드의 변형이라고 생각해도 무방합니다. 현대에는 CBC, CTR 모드를 주로 사용하고 있기 때문에 다른 모드는 다루지 않겠습니다.
DES
블록 암호의 운용 방식을 알았으니 이제는 실제 블록 암호의 예시를 알아봅시다. DES(Data Encryption Standard)는 64비트 블록 단위를 암호화하는 알고리즘으로, 1975년에 IBM에서 개발했고 1979년에 미국에서 국가 표준으로 지정되었습니다.
DES 알고리즘에서 활용되는 키는 56비트이고 암호를 만들 당시에는 충분한 길이였으나 컴퓨터의 성능이 점차 개선됨에 따라 DES는 자체적인 취약점이 발견되지 않았음에도 불구하고 키가 짧아 2016년에 들어서는 GeForce GTX 1080 Ti GPU로 모든 키를 30일 이내에 확인할 수 있는 상황이 되어 더 이상 제 기능을 할 수 없는 암호 알고리즘이 되었습니다.
DES의 구조
비록 현대에 들어서 키의 길이가 짧아 DES 알고리즘은 안전하지 않지만, 그럼에도 불구하고 알고리즘의 구조를 공부하는 것은 암호학적 지식을 넓히는 것에 큰 도움이 됩니다. DES는 Feistel 구조를 가집니다. Feistel 구조의 가장 큰 특징은 암호화/복호화 과정에서 역함수가 존재하지 않는 라운드 함수를 거친다는 점입니다. 상식적으로 여러 함수를 거쳐서 암호화를 진행했다면 복호화 과정에서는 암호문을 가지고 해당 함수들의 역함수를 거쳐야할텐데, Feistel 구조에서는 라운드 함수가 역함수가 존재하지 않아도 상관없습니다.
Feistel 구조의 암호화 과정은 아래와 같습니다. $L_{i+1} = R_i$ $R_{i+1} = L_{i} \oplus F(R_i, K_i)$
이 때 F가 라운드 함수입니다. 그리고 복호화 과정은 아래와 같습니다. $R_i = L_{i+1}$ $L_i = R_{i+1} \oplus F(L_{i+1}, K_i)$
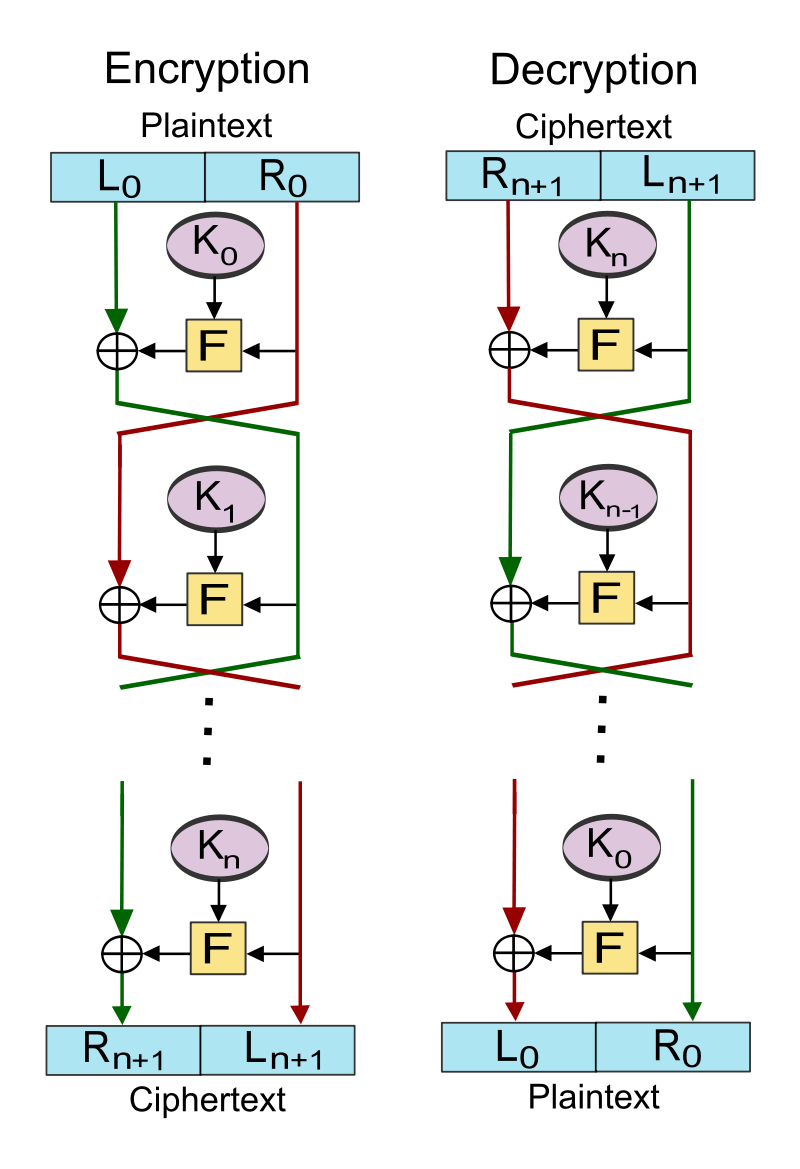
복호화 과정을 보면 F의 역함수가 필요하지 않음을 알 수 있습니다. 그리고 식의 형태를 보면 암호화와 복호화가 완전히 동일한 형태라는걸 알 수 있는데, 실제로 암호화와 복호화는 키의 적용 순서만 달라질 뿐 동일한 함수에서 처리가 가능하다는 장점도 있습니다.
DES의 구조도 위의 그림과 동일합니다. DES는 맨 처음과 끝에서 비트 단위의 Permutation을 제외하면 총 16 라운드의 Feistel 구조로 이루어져있습니다. 라운드 함수는 32비트의 $R$과 키 48비트를 입력받아 32비트를 출력합니다. 라운드 함수는 Expansion, S-box, Permutation 이 3가지 과정으로 이루어져있으나 과정 각각에 대해 설명하는 것은 크게 중요한 내용이 아니라고 판단되어 넘어가겠습니다.
DES의 취약점
앞에서 소개한 것과 같이 키의 길이가 짧음으로 인해 취약점이 발생합니다. 그리고 여기서 추가로 소개할 내용은 공격의 시간복잡도를 $2^{56}$보다 줄일 수 있는 내용입니다. 내용을 이해하고 싶으면 Differential Cryptanalysis(차분 공격), Linear Cryptanalysis(선형 공격)에 대한 이해가 선행되어야 하나 이 두 공격은 포스팅 하나 안에서 짧게 다루기에는 너무 분량이 많기 때문에 자세한 언급 없이 넘어가겠습니다.
DES가 공개될 당시에는 차분 공격이라는 개념이 없었습니다. 그런데 1980년대 후반 Eli Biham과 Adi Shamir가 차분 공격을 찾아낸 이후 DES가 차분 공격을 고려해 설계했음을 IBM, NSA 측에서 밝혔습니다. 그러나 계속된 연구 끝에 Eli Biham, Adi Shamir가 1993년 DES가 차분 공격으로 $2^{47}$개의 chosen plaintext로부터 $O(2^{37})$에 키를 찾을 수 있음을 밝혀냈고 또 Mitsuru Matsui가 선형 공격으로 $2^{43}$개의 known plaintext로부터 키를 찾을 수 있음을 밝혀냈습니다. (차분 공격에 대한 추가적인 설명)
3DES
DES는 1997년 RSA Security에서 제시한 DES Challenges가 깨지고, 1998년 DES에 최적화된 하드웨어로 56시간만에 키를 찾는 등의 일이 계속 발행하면서 대체할 필요성이 제기되었습니다. 그로 인해 1997년 NIST는 DES를 대체할 AES(Advanced Encryption Standard)를 공모하지만, AES가 선정되기 전까지 임시로 DES를 변형해 3DES를 만들어 더 안전하도록 만들었습니다.
3DES는 DES의 서로 다른 키 3개를 정해 DES를 3번 수행하는 알고리즘입니다. 구체적으로 키 $K_1, K_2, K_3$에 대해 $3DES(M) = ENC_{K1}(DEC_{K2}(ENC_{K3}(M)))$입니다. 굳이 $K_2$에 대해 $ENC$ 대신 $DEC$를 하는 이유는 3DES를 이용해 DES를 키 $K$로 암호화하고 싶을 때 $K_1, K_2, K_3$를 모두 $K$로 두면 되므로 backward compatibility를 제공하기 위해서입니다. 이를 통해 키의 길이를 56비트에서 168비트로 늘이는 효과를 낼 수 있습니다. 그러나 3DES를 공격하는 시간복잡도가 $O(2^{168})$로 늘어나지는 않고 대략 $O(2^{120})$ 정도입니다. 이는 MITM(Meet In The Middle Attack) 때문입니다. 2DES가 DES에 비해 그다지 안전하지 않은 이유 또한 2DES는 키의 길이가 2배이지만 MITM으로 인해 $O(2^{64})$ 정도로밖에 시간복잡도가 늘지 않기 때문입니다. MITM에 대한 자세한 설명은 생략하겠습니다.
3DES는 DES를 3번 적용하기 때문에 속도가 느리고 뒤에 소개할 AES보다 덜 안전하지만, DES만큼 개인이 하루 내로 키를 복원할 수 있는 정도는 아니기 때문에 Microsoft Outlook, Firefox, OpenSSL 등에서도 3DES는 여전히 사용할 수 있습니다.
AES
AES는 DES가 더 이상 안전하지 않게 되면서 NIST가 주최한 공모전에서 선정된 Rijndael 알고리즘입니다. AES는 공모전에 출품된 수많은 후보 중에서 안전한 정도, 속도, 소프트웨어/하드웨어 퍼포먼스 등을 종합적으로 고려해 선정된 알고리즘이고 현재까지도 Full Round에 대해서는 전수조사보다 겨우 4배정도 빠른 방법만이 찾아졌을 뿐 밝혀진 효과적인 공격이 없기 때문에 안전합니다.(논문 링크)
DES가 Feistel 구조를 사용한 것과 같이 AES는 SPN(Substitution-Permutation Network) 구조를 사용합니다. SPN 구조는 별다른게 아니라 Substitution과 Permutation을 여러 라운드에 걸쳐 적용하는 구조입니다. Substitution과 Permutation은 고전 암호에서도 찾아볼 수 있는 기법이기에 SPN 구조가 과연 안전한가 의문이 들 수도 있지만 중간에 키를 XOR해가며 여러 라운드에 걸쳐 사용하면 굉장히 공격하기가 어려운 구조가 만들어집니다.
AES는 블록 크기가 16바이트로 이를 $4 \times 4$의 이차원 행렬로 만들어 Substitution과 Permutation을 수행합니다. 한 라운드는 SubBytes, ShiftRows, MixColumns, AddRoundKey로 이루어져있고 MixColumns에서 필요한 갈루아 필드 상의 연산을 제외하면 전부 이해하기 어렵지 않은 연산들입니다. 각 연산에 대한 자세한 설명은 생략하겠습니다.
결론
이번 포스트에서는 블록 암호에 대해 알아보았습니다. 대회에서 블록 암호와 관련한 문제가 나왔을 때 그 암호가 새롭게 구현된 형태이면 일단 흐름을 따라가면서 취약점을 찾아보고, 도저히 취약점이 찾아지지 않는다면 차분/선형 분석을 시도해보아야 합니다. 만약 블록 암호의 코드가 공개되어있지 않거나 AES, 3DES와 같이 안전함이 입증된 알고리즘이 주어졌을 경우에는 운용 방식에 관한 문제일 가능성을 생각해야 합니다.