Mo's Algorithm
개요
Mo’s algorithm은 평방 분할 (sqrt decomposition)의 일종의 활용 기법으로, 오프라인으로 구간 쿼리 문제를 해결할 때 사용할 수 있습니다. 어떤 구간에 대한 정보를 빠르게 얻기 어려워 그 구간에 속한 $O(N)$개의 원소를 매번 모두 확인해야 하는 경우, $Q$개의 쿼리를 나이브하게 처리하려면 $O(QN)$의 시간이 소요될 것을 $O((N+Q)sqrt(N))$ 시간에 해결할 수 있게 해주는 마법의(?) 알고리즘입니다.
평방 분할 (sqrt decomposition)
우선 평방 분할에 대해 간단하게 소개하겠습니다. 평방 분할은 길이 $N$인 전체 구간을 $\sqrt N$개의 같은 크기의 블록으로 쪼개는 기법입니다. 이게 어떻게 유용해질 수 있는지 알아보기 위해, 문제를 하나 예시로 보겠습니다.
구간 합 구하기
- https://www.acmicpc.net/problem/2042
이 문제는 전형적인 세그먼트 트리 문제로 많이 제시되지만, 평방 분할로도 비교적 쉽게 해결이 가능한 문제입니다. 평범하게 2번 쿼리마다 구간 내에 있는 모든 수의 합을 구하려고 하면 $O(M+NK)$로 시간 초과를 피할 수 없을 것입니다. 세그먼트 트리는 이에 $O(N+(M+K)logN)$ 해법을 제시하지만, 평방 분할 기법을 이용하면 조금 다른 형태로 문제의 제한에 맞는 풀이를 만들어낼 수 있습니다.
우선 길이 $N$인 전체 구간을 $\sqrt N$개의 같은 크기의 블록으로 쪼개면, 각 블록의 크기 역시 $\sqrt N$이 됩니다. 각 블록의 합을 저장하는 배열을 block이라 이름지어봅시다. 처음에 배열의 내용을 입력받은 후 이 값들을 미리 계산해 둡니다..
using ll = long long;
int rt;
ll arr[1000001];
ll block[1005];
...
int n, m, k, i;
cin >> n >> m >> k;
rt = (int)sqrt(n);
for (i = 1; i <= n; i++)
{
cin >> arr[i];
block[i / rt] += arr[i];
}
i번째 인덱스는 i/sqrt(N)번째 블록에 속하게 됩니다. 그림으로 표현하면 다음과 같습니다.

이제 1번 쿼리에 대한 처리는 간단합니다. b번째 수를 c로 바꾸는 연산은 변화량만큼을 arr[b]와 block[b / rt]에 각각 더해주는 것으로 충분합니다. 이 연산은 물론 $O(1)$ 시간을 소요합니다.
int a, b, c;
cin >> a >> b >> c;
if (a == 1)
{
ll diff = c - arr[b];
arr[b] += diff;
block[b / rt] += diff;
}
이제 2번 쿼리를 처리해 봅시다. 2번 쿼리를 처리할 때는 원소를 세 종류로 나누어서 개별적으로 처리를 해야 합니다.
- 블록의 일부만 구간에 속한 왼쪽 끝의 원소들
- 블록의 일부만 구간에 속한 오른쪽 끝의 원소들
- 블록 전체가 구간에 속한 원소들
무슨 뜻인지 잘 이해되지 않는다면, 다음 그림을 봅시다.

투명한 구간이 합을 구하려는 구간일 때, 각 원소들이 어디에 속하는지를 나타낸 그림입니다. 1로 표시된 원소들은 0번째 블록에 속하지만 0번째 블록의 모든 원소들이 구간에 속하지는 않습니다. 마찬가지로 2로 표시된 원소는 3번째 블록에 속하지만 3번째 블록의 모든 원소들이 구간에 속하지는 않습니다. 이 원소들은 모두 개별적으로 합을 구해줍니다.
ll ans = 0;
while (b % rt != 0 && b <= c)
ans += arr[b++];
while (c % rt != rt - 1 && c >= b)
ans += arr[c--];
b가 rt로 나누어 떨어지는 순간이 그 지점이 블록의 시작점이 되는 순간이므로 그 직전까지만 더해주고, c를 rt로 나눈 나머지가 rt-1이 되는 순간이 그 지점이 블록의 마지막 지점이 되는 순간이므로 그 직전까지만 먼저 더해 줍니다.
마지막으로 3번에 속하는 원소들의 합을 구할 때는 위에서 만들어 둔 블록들을 사용합니다. 3번에 속하는 원소들의 합은 이미 그 원소들이 속한 블록에 저장되어 있으므로 그대로 더해주면 됩니다. rt개씩 건너뛰면서 그 원소가 속한 블록에 저장된 값을 더해줍니다.
while (b <= c)
{
ans += block[b / rt];
b += rt;
}
그러면 2번 쿼리의 시간복잡도는 어떻게 될까요? 1번, 2번에 속하는 원소들은 각각 많아야 $O(\sqrt N)$개이므로, 둘을 합해도 $O(\sqrt N)$번의 연산을 하게 됩니다. 3번에 속하는 원소들 역시 $O(\sqrt N\)$개의 블록만 보면 되기 때문에, 2번 쿼리 전체의 시간복잡도 역시 $O(\sqrt N)$이 됩니다.
따라서 이 코드의 총 시간복잡도는 $O(N+M+K\sqrt N)$이 됩니다. $log$만큼 아름다운 복잡도는 아니지만, 충분히 강력한 시간복잡도 단축을 해냈다고 볼 수 있습니다.
전체 코드는 아래와 같습니다.
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
using ll = long long;
int rt;
ll arr[1000001];
ll block[1005];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n, m, k, i;
cin >> n >> m >> k;
rt = (int)sqrt(n);
for (i = 1; i <= n; i++)
{
cin >> arr[i];
block[i / rt] += arr[i];
}
for (i = 0; i < m + k; i++)
{
int a, b, c;
cin >> a >> b >> c;
if (a == 1)
{
ll diff = c - arr[b];
arr[b] += diff;
block[b / rt] += diff;
}
else
{
ll ans = 0;
while (b % rt != 0 && b <= c)
ans += arr[b++];
while (c % rt != rt - 1 && c >= b)
ans += arr[c--];
while (b <= c)
{
ans += block[b / rt];
b += rt;
}
cout << ans << '\n';
}
}
}
Mo’s algorithm
이제 Mo’s algorithm이 도대체 무엇인지 알아봅시다. 이번에도 이 알고리즘을 적용할 수 있는 대표적인 문제를 하나 보면서 설명을 진행하겠습니다.
수열과 쿼리 5
- https://www.acmicpc.net/problem/13547
문제 자체는 단순하지만 최적화를 시키는 것은 간단치 않습니다. 먼저 각각의 쿼리를 개별적으로 나이브하게 처리한다고 생각해 봅시다. 우리는 이런 방법을 생각해볼 수 있습니다.
1에서 100만까지 각 수가 몇 번 등장했는지를 세는 배열을 만들고, 구간 내의 원소를 하나씩 보면서 그 원소가 처음으로 등장한 경우에만 답을 증가시킨다.
물론 이런 방법을 사용하면 매 쿼리마다 최대 $O(N)$개의 원소를 봐야 하므로 $O(NM)$의 시간복잡도가 되어 시간 초과를 받게 될 것입니다. 그렇다면 이건 어떨까요? 이전 쿼리의 구간에 대한 정보를 들고 있는 상태에서 새 쿼리의 구간으로 넘어갈 때 배열을 초기화하지 않고 포인터를 옮겨가면서 정보를 갱신해주는 것입니다.
이전 쿼리의 왼쪽 끝 포인터를 새 쿼리의 왼쪽 끝으로 한 칸씩 옮겨가고, 이전 쿼리의 오른쪽 끝 포인터를 새 쿼리의 오른쪽 끝으로 한 칸씩 옮겨가며 카운트를 갱신한다. 새 원소가 구간에 포함되는 경우 그 원소 값의 카운트가 0이었다면 답을 증가시키고, 기존 원소가 구간에서 제외되는 경우 그 원소 값의 카운트가 1이었다면 답을 감소시킨다.
여기까지를 코드로 표현하면 다음과 같이 됩니다.
int cnt[1000001];
int arr[100001], ans[100001];
int cur;
struct query {
int l, r, n;
} q[100001];
void f(int index, bool add)
{
if (add)
{
if (cnt[arr[index]]++ == 0)
cur++;
}
else
{
if (--cnt[arr[index]] == 0)
cur--;
}
}
...
int lo = 1, hi = 0;
for (i = 0; i < m; i++)
{
while (q[i].l < lo)
f(--lo, true);
while (q[i].l > lo)
f(lo++, false);
while (q[i].r < hi)
f(hi--, false);
while (q[i].r > hi)
f(++hi, true);
ans[q[i].n] = cur;
}
이렇게 하면 비슷한 구간을 묻는 쿼리가 연속으로 들어올 때 전체 원소를 보지 않고 새로 구간에 추가 또는 제거되는 원소들만 확인해주면 되기 때문에, 즉 기존의 정보를 재활용하기 때문에 분명 장점은 있습니다. 그러나 이것으로는 불충분합니다. 매 쿼리 사이에서 각 포인터가 최대 $O(N)$번을 움직여야 하기 때문에 최악의 경우 시간복잡도가 $O(NM)$인 것은 변하지 않기 때문입니다.
그러면 그 다음 목표는, 이전의 정보가 최대한 다음 쿼리에서 재활용이 잘 될 수 있도록 쿼리를 정렬해서 오프라인으로 처리해주는 것입니다. 쉽게 떠오르는 평범한 정렬 기준으로, 왼쪽 작은 순 -> 오른쪽 작은 순으로 정렬해주는 다음 비교 함수를 생각해 봅시다.
struct query {
int l, r, n;
bool operator<(const query &o) const {
return l == o.l ? r < o.r : l < o.l;
}
} q[100001];
이제 최소한 l 포인터는 쿼리 전체에서 총 $O(N)$번 넘게 움직이지 않는다는 것이 명확해졌습니다. 하지만 r 포인터는 어떨까요? 다음과 같은 상황을 가정해 봅시다.
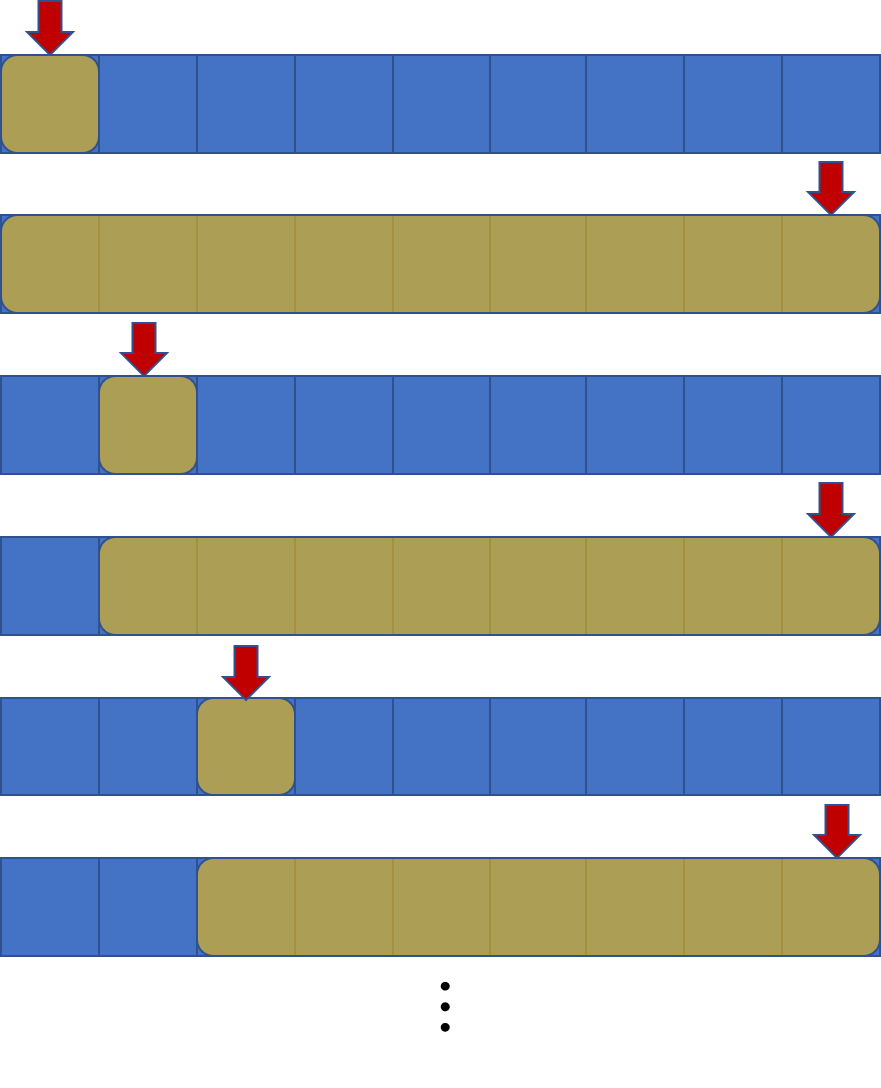
애석하게도, r 포인터는 매 쿼리마다 이렇게 널뛰기를 하고 말게 됩니다. 쿼리마다 $O(N)$번을 움직이게 되니, 최악의 경우 역시 $O(NM)$이 되는 것을 피할 수 없습니다.
이런 극단적인 움직임을 피하고, 어떠한 상황에서도 안정적인 시간 내에 이러한 쿼리를 수행하는 방법이 없을까요? 여기에서 Mo’s algorithm이 빛을 발하게 됩니다.
위에서 살펴본 평방 분할에 대해 생각해 봅시다. 전체를 $\sqrt N$개의 블록으로 쪼개면, 각 블록 내에서 하나의 포인터를 움직일 때의 최대 이동 횟수도 $O(\sqrt N)$임이 자명합니다. 이 성질을 이용해서, 다음과 같이 쿼리를 정렬해 봅시다.
쿼리의 오른쪽 끝이 속한 블록 이 증가하는 순서대로, 블록 이 같으면 왼쪽 끝이 증가하는 순서대로 정렬한다.
코드로 표현하면 다음과 같습니다.
struct query {
int l, r, n;
bool operator<(const query &o) const {
int x = r / rt;
int y = o.r / rt;
return x == y ? l < o.l : x < y;
}
} q[100001];
이와 같은 방법으로 위의 경우를 정렬하면 다음과 같이 됩니다.
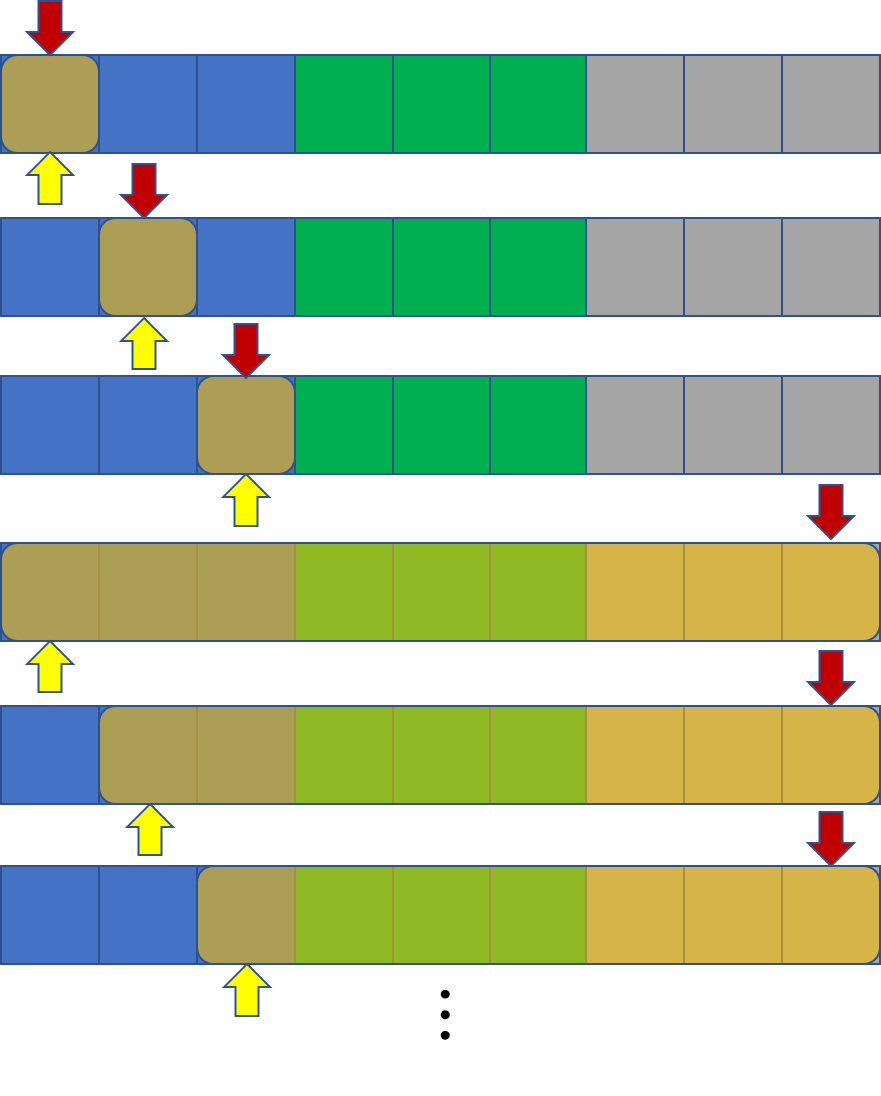
이렇게 정렬했을 때의 시간복잡도를 분석해 봅시다. 먼저 r 포인터의 움직임은 두 종류가 있는데, 하나는 r이 같은 블록 내에서 움직이는 것이고, 다른 하나는 r이 다른 블록으로 넘어가는 것입니다. 같은 블록 내에서 움직일 때의 최대 이동 횟수는 $O(\sqrt N)$이 명확합니다. 그러면 다른 블록으로 움직이는 경우는 어떨까요? 한 번에 최대 $O(N)$ 칸을 움직여야 할 수도 있지만, 좀 더 크게 보면 전체 쿼리를 수행하는 데에 블록 사이를 건너가기 위해 이동하는 총 횟수도 $O(N)$입니다. 즉, 쿼리를 M개 수행하기 위해 매 쿼리당 $O(\sqrt N)$개를 움직이고 전체 과정에서 $O(N)$번의 추가 이동이 있으니, 총 $O(N+M\sqrt N)$번의 이동만이 발생하게 됩니다.
그러면 l 포인터의 이동은 어떻게 될까요? l 포인터는 r 포인터가 같은 블록에 속해있을 때는 오름차순으로 정렬이 되어 있습니다. 즉, r이 같은 블록에 속한 동안 l은 총 $O(N)$번 움직입니다. 그런데 r 포인터가 다른 블록으로 옮겨가는 일이 $O(\sqrt N)$번 있으니, l 포인터는 총 $O(N\sqrt N)$번 움직이게 됩니다.
따라서 Mo’s algorithm을 사용하면 총 $O((N+M)\sqrt N)$ 시간에 문제를 해결할 수 있습니다. 정말로 마법같은 일이 아닐 수 없습니다.
전체 코드는 아래와 같습니다.
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
int rt;
int cnt[1000001];
int arr[100001], ans[100001];
int cur;
struct query {
int l, r, n;
bool operator<(const query &o) const {
int x = r / rt;
int y = o.r / rt;
return x == y ? l < o.l : x < y;
}
} q[100001];
void f(int index, bool add)
{
if (add)
{
if (cnt[arr[index]]++ == 0)
cur++;
}
else
{
if (--cnt[arr[index]] == 0)
cur--;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n, m, i;
cin >> n;
rt = (int)sqrt(n);
for (i = 1; i <= n; i++)
cin >> arr[i];
cin >> m;
for (i = 0; i < m; i++)
{
cin >> q[i].l >> q[i].r;
q[i].n = i;
}
sort(q, q + m);
int lo = 1, hi = 0;
for (i = 0; i < m; i++)
{
while (q[i].l < lo)
f(--lo, true);
while (q[i].l > lo)
f(lo++, false);
while (q[i].r < hi)
f(hi--, false);
while (q[i].r > hi)
f(++hi, true);
ans[q[i].n] = cur;
}
for (i = 0; i < m; i++)
cout << ans[i] << '\n';
}
백설공주와 난쟁이
- https://www.acmicpc.net/problem/2912
이 문제는 조금 다른 방향의 접근으로1 쉽게 해결하는 방법도 있지만, Mo’s algorithm을 적용해서도 해결할 수 있습니다. 수열과 쿼리 5 문제와 비슷하게 각 구간에 대한 정보를 빠른 시간 내에 얻기는 어렵지만, 기존의 정보를 재활용할 수 있다는 점에서 이 알고리즘을 쓰기에 적절한 문제라고 할 수 있습니다.
M과 C의 범위가 크지 않기 때문에 매 쿼리마다 모든 색에 대한 개수를 세는 것은 문제가 되지 않습니다. 대신, 쿼리에서 확인하는 범위의 변동이 커지지 않도록 Mo’s algorithm을 적용해서 쿼리를 정렬해 봅시다.
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int n, sz, c, m;
int cnt[10001], a[300001];
struct A {
int l, r, n;
bool operator<(const A &o) const {
int x = r / sz;
int y = o.r / sz;
return x == y ? l < o.l : x < y;
}
} q[10000];
int ans[10000];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int i, j;
cin >> n >> c;
sz = (int)sqrt(n);
for (i = 1; i <= n; i++)
cin >> a[i];
cin >> m;
for (i = 0; i < m; i++)
{
cin >> q[i].l >> q[i].r;
q[i].n = i;
}
sort(q, q + m);
int lo = 1, hi = 0;
for (i = 0; i < m; i++)
{
while (q[i].l < lo)
cnt[a[--lo]]++;
while (q[i].l > lo)
cnt[a[lo++]]--;
while (q[i].r < hi)
cnt[a[hi--]]--;
while (q[i].r > hi)
cnt[a[++hi]]++;
for (j = 1; j <= c; j++)
if (cnt[j] > (hi - lo + 1) / 2)
break;
if (j <= c)
ans[q[i].n] = j;
}
for (i = 0; i < m; i++)
{
if (ans[i])
cout << "yes " << ans[i] << '\n';
else
cout << "no\n";
}
}
이제 많은 구간 쿼리 문제들을 Mo’s algorithm을 이용해 멋지게 시간복잡도를 단축해 풀 수 있을 것입니다!
-
(스포일러) 모자 색마다 난쟁이의 위치를 순서대로 저장하는 배열을 만들고, 각 쿼리마다 구간 내의 인덱스를 랜덤으로 뽑은 뒤 이분 탐색으로 그 색의 모자를 쓴 난쟁이가 범위 내에 절반을 넘게 있는지를 확인하는 작업을 50번 정도 반복하면 답이 yes인 쿼리에서 해당 색을 찾아내지 못할 확률이 1/2^50도 되지 않기 때문에 맞는 풀이라고 할 수 있습니다. ↩