최소 외접원 찾기
서론
최소 외접원 문제는, 2차원 평면 상에 점이 $N$개가 있을 때, 이들을 모두 담는 최소 반지름의 원이 과연 무엇인지를 찾는 문제입니다. 실생활에서 굉장히 많이 사용될 수 있는 문제이며, 예를 들면, 어떤 도시에 기지국을 지어야 하는데, 어느 곳에 지어야 송신소를 모두에게 도달하면서, 최소한의 반지름으로 모든 송신소를 덮을 수 있는 지 등, 효율적인 배치에 관한 문제입니다. 이 게시글에서는 이 문제를 $O(N)$에 푸는 방법을 소개 합니다.
담금질 기법

담금질 기법은, 원래는 모든 최적화 문제에 사용되는 기법입니다. 담금질 기법은, 일반적인 문제에서, 현재 답의 근처 해를 적당히 찾고, 해가 더 좋아질 경우에는 갱신하고, 해가 좋아지지 않을 경우에는 확률적으로 갱신하는 방법입니다. 이 담금질 기법은 다항시간에 해를 찾을 수 없는 문제에 대해, 적당히 좋은 해를 찾기 위해 사용되는 방법입니다. 해가 좋아지지 않을 경우에 확률적으로 갱신 하는 이유는, 지역 최적해에 빠지지 않기 위해서입니다. 하지만 이 문제에 대해서는, 지역 최적해가 곧 전역 최적해가 됩니다. 왜냐하면, 거리 함수는 아래로 볼록인 함수이고, 이 아래로 볼록인 함수를 최솟값을 사용해도 다시 아래로 볼록인 함수가 나오기 때문에, 이 문제는 전역 최적해를 찾는 문제로 바뀌게 됩니다.
그렇게 코드를 작성하면, 결국엔 적당한 해를 하나 찾은 이후에 계속 줄여나가는 방법을 쓰게 됩니다. 시간 복잡도는 기본적으로 $O(N)$ 이지만, 오차에 반비례하는 항을 가집니다. 아래 구현은 2차원에서의 구현이지만, 이 구현의 장점은 3차원 이상에서도 사용할 수 있고, 거리 함수가 다른 볼록함수로 바뀌어도 계속 적용할 수 있습니다.
double enclosing_sphere(vector<double> x, vector<double> y){
int n = x.size();
auto hyp = [](double x, double y){
return x * x + y * y + z * z;
};
double px = 0, py = 0;
for(int i=0; i<n; i++){
px += x[i];
py += y[i];
}
px *= 1.0 / n;
py *= 1.0 / n;
double rat = 0.1, maxv;
for(int i=0; i<10000; i++){
maxv = -1;
int maxp = -1;
for(int j=0; j<n; j++){
double tmp = hyp(x[j] - px, y[j] - py);
if(maxv < tmp){
maxv = tmp;
maxp = j;
}
}
px += (x[maxp] - px) * rat;
py += (y[maxp] - py) * rat;
rat *= 0.998;
}
return sqrt(maxv);
}
기하학적 방법
기하학적 방법은 먼저 여러가지 관찰들이 필요합니다.
- 최소 외접원은 2개 이상의 점을 포합합니다.
증명. 최소 외접원이 0개의 점을 포함 할 경우, 반지름을 매우 작은 양 만큼 줄이면 더 작은 원을 만들 수 있고, 최소 외접원이 1개의 점을 포함할 경우, 중심을 1개의 점쪽으로 매우 작은 양 만큼 옮기고, 반지름을 매우 작은 양 만큼 줄이면, 새로운 원을 만들 수 있습니다.
매우 작은 양이라고 애매하게 서술 되어 있지만, 거리 함수를 이용하여, 좀 더 엄밀하게 증명을 할 수도 있습니다.
- 최소 외접원이 정확히 2개의 점을 포함하고 있으면, 중심은 그 두 점의 중점에 위치합니다.
증명. 이도 마찬가지로, 중심이 정확히 2개의 점을 포함하고 있지 않으면, 그 중점쪽으로 매우 작은 양 만큼 옮겨 주는 것으로 새로운 더 작은 원을 만들 수 있습니다.
- 최소 외접원이 3개 이상의 점을 포함하고 있으면, 그 원은 3개 이상의 점 중 임의의 3개의 외접원 입니다.
증명. 정해진 세 점이 위에 올라와있는 원은 외접원으로 유일하기 때문에, 이 밖에는 존재할 수가 없습니다.
우리는 이 증명으로 일단 가장 나이브 한 $O(N^4)$ 풀이를 찾을 수 있습니다.
네제곱 풀이
풀이는 먼저, $N$ 개의 점 중에서 가능한 답이 2개의 점을 포함하는 중심이라는것과, 3개의 점을 포함하는 외접원 중 하나라는 것입니다. 가능한 답의 후보가, $\binom{N}{2} + \binom{N}{3}$ 개이므로, 이에 대해서 원에 포함되는지에 대한 여부를 $O(N)$에 검사하면, 다항시간에 정확한 답을 찾을 수 있습니다.
외접원은, 세 점 A, B, C가 주어 졌을 때, 다음 식으로 구할 수 있고, 중복된 부분을 전부다 제거하고 코드로 구현하면 다음과 같은 꼴이 나옵니다. 외접원의 좌표를 구하는 법은 A, B, C로 부터의 거리가 같은 점의 좌표를 나타내는 3원 2차 방정식을 열심히 전개해서 정리해주면 됩니다.
$D = 2\left[A_x\left(B_y - C_y\right) + B_x\left(C_y - A_y\right) + C_x\left(A_y - B_y\right)\right]$
$U_x = \frac{1}{D}\left[\left(A_x^2 + A_y^2\right)\left(B_y - C_y\right) + \left(B_x^2 + B_y^2\right)\left(C_y - A_y\right) + \left(C_x^2 + C_y^2\right)\left(A_y - B_y\right)\right]$
$U_y = \frac{1}{D}\left[\left(A_x^2 + A_y^2\right)\left(C_x - B_x\right) + \left(B_x^2 + B_y^2\right)\left(A_x - C_x\right) + \left(C_x^2 + C_y^2\right)\left(B_x - A_x\right)\right]$
double eps = 1e-9;
using Point = complex<double>;
struct Circle{ Point p; double r; };
Circle INVAL = Circle{Point(0, 0), -1};
Circle mCC(Point a, Point b, Point c){
b -= a; c -= a;
double d = 2*(conj(b)*c).imag(); if(abs(d)<eps) return INVAL;
Point ans = (c*norm(b) - b*norm(c)) * Point(0, -1) / d;
return Circle{a + ans, abs(ans)};
}
INVAL 은 올바르지 않은 원 (세 점이 한 직선 위에 있음)을 나타내고, Point 는 C++의 <complex> 에 있는 복소수를, 복소평면으로 나타낸 것 입니다. 이렇게 사용할 경우에, 두 벡터의 내적, 외적, 크기 등을 내장함수로 간단하게 구할 수 있다는 장점이 있습니다.
그래서 코드를 살펴 보면 다음과 같이 간단하게 구할 수 있습니다.
bool in(const Circle& c, Point p){ return dist(c.p, p) < c.r + eps; }
bool allin(const Circle& c, const vector<Point> &v){
for(auto p: v)
if(!in(c, p))
return false;
return true;
}
Circle solve(vector<Point> p) {
Circle ans = INVAL;
if(p.size()==1) return Circle{p[0], 0};
for(int i=0; i<(int)p.size(); ++i)
for(int j=0; j<i; ++j)
{
Circle c = Circle{(p[i]+p[j])/2, abs(p[i]-p[j])/2};
if(allin(c, p) && (ans.r<0||ans.r>c.r)) ans = c;
for(int k=0; k<j; ++k)
{
c = mCC(p[i], p[j], p[k]);
if(allin(c, p) && (ans.r<0||ans.r>c.r)) ans = c;
}
}
return ans;
}
세제곱? 풀이
우리는 이제 좀 더 다른 관찰을 해야 합니다.
우리가 만약에 점 하나의 위치를 안다면? 우리가 봐야할 원의 후보는 $O(N^2)$ 개로 줄어들게 됩니다.
점의 위치를 하나 더 알게 되면, 우리가 봐야 할 원의 후보는 $O(N)$개로 줄게 됩니다. 우리가 여기서 할 수 있는 관찰은, 이 봐야할 원의 중심들이 모두 다 한 직선 위에 있다는 점입니다.
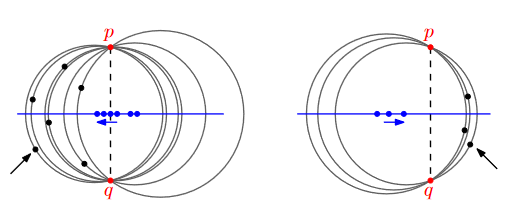
그래서, 왼쪽에 있는 점들 중에서는 가장 왼쪽에 중심이 위치한 점들만, 오른쪽에 있는 점들 중에서는 가장 오른쪽에 위치한 점들만 보아주면 됩니다.
만약 이걸 두 점을 고정하고 새로 추가하는 방식으로 구현을 한다면, 왼쪽과 오른쪽의 점을 따로 관리해주면서, 원에 포함되지 않은 더 왼쪽의 점이 나오면 점을 추가하고, 오른쪽도 마찬가지로 구현을 하면, 시간 복잡도 $O(N)$ 에 두개의 점이 고정되었을 때의 모든 원을 찾을 수 있습니다.
그래서 이 구현을 옮겨보면
double dist(Point p, Point q){ return abs(p-q); }
double area2(Point p, Point q){ return (conj(p)*q).imag(); }
Circle solve(vector<Point> p) {
Circle c = INVAL;
for(int i=0; i<p.size(); ++i) if(c.r<0 ||!in(c, p[i])){
c = Circle{p[i], 0};
for(int j=0; j<=i; ++j) if(!in(c, p[j])){
Circle ans{(p[i]+p[j])*0.5, dist(p[i], p[j])*0.5};
if(c.r == 0) { c = ans; continue; }
Circle l, r; l = r = INVAL;
Point pq = p[j]-p[i];
for(int k=0; k<=j; ++k) if(!in(ans, p[k])) {
double a2 = area2(pq, p[k]-p[i]);
Circle c = mCC(p[i], p[j], p[k]);
if(c.r<0) continue;
else if(a2 > 0 && (l.r<0||area2(pq, c.p-p[i]) > area2(pq, l.p-p[i]))) l = c;
else if(a2 < 0 && (r.r<0||area2(pq, c.p-p[i]) < area2(pq, r.p-p[i]))) r = c;
}
if(l.r<0&&r.r<0) c = ans;
else if(l.r<0) c = r;
else if(r.r<0) c = l;
else c = l.r<=r.r?l:r;
}
}
return c;
}
다음과 같은 구현이 되며, 시간 복잡도는, 루프가 3중루프이기 때문에 $O(N^3)$ 이 걸리게 됩니다.
평균 시간복잡도 분석과 O(N) 알고리즘
근데, 이 풀이는 for문 전체를 들어가지 않는 if문이 굉장히 많습니다.
$N$ 개의 점 중 어떤 한 점이, 최소 외접원 위에 있을 확률은 $O(\frac{1}{N})$ 입니다. 이 말은, 내부 루프를 돌 시간복잡도를 다시 계산 해 볼 수 있다는 것입니다.
이 문제에서 5번줄과 7번 줄에 분기가 있습니다. 7번줄의 분기를 들어갈 확률은, 평균적으로 $O(\frac{1}{j+1})$이고, 들어간 경우에는 $O(j)$ 번의 시간이 12번 줄에서 사용 되니까, 이 루프 내부의 평균 시간복잡도는 $O(1)$이 되게 됩니다!
실은 이 시간이 오래걸릴거라고 생각되었던 알고리즘은, 최소 외접원을 구성하는 점이 상수개라는 점으로 시간 복잡도 분석을 향상시킬수 있습니다.
마찬가지로, 5번 루프도, 내부 코드의 평균 시간복잡도가 $O(1)$ 이므로, 총 시간 복잡도는 $O(N)$ 이라고 할 수 있습니다. 평균 시간복잡도에 동작하는 알고리즘을 만들어주기 위해서 해야 할 것은, 배열을 섞어주는 것입니다.
코드
그렇게 작성한 코드는 다음과 같고, 자칫 어려울 수도 있는 알고리즘을 C++의 std::complex 의 강력한 복소수 곱셈등을 사용하여 구현하면 다음과 같습니다:
namespace cover_2d{
double eps = 1e-9;
using Point = complex<double>;
struct Circle{ Point p; double r; };
double dist(Point p, Point q){ return abs(p-q); }
double area2(Point p, Point q){ return (conj(p)*q).imag(); }
bool in(const Circle& c, Point p){ return dist(c.p, p) < c.r + eps; }
Circle INVAL = Circle{Point(0, 0), -1};
Circle mCC(Point a, Point b, Point c){
b -= a; c -= a;
double d = 2*(conj(b)*c).imag(); if(abs(d)<eps) return INVAL;
Point ans = (c*norm(b) - b*norm(c)) * Point(0, -1) / d;
return Circle{a + ans, abs(ans)};
}
Circle solve(vector<Point> p) {
mt19937 gen(0x94949); shuffle(p.begin(), p.end(), gen);
Circle c = INVAL;
for(int i=0; i<p.size(); ++i) if(c.r<0 ||!in(c, p[i])){
c = Circle{p[i], 0};
for(int j=0; j<=i; ++j) if(!in(c, p[j])){
Circle ans{(p[i]+p[j])*0.5, dist(p[i], p[j])*0.5};
if(c.r == 0) { c = ans; continue; }
Circle l, r; l = r = INVAL;
Point pq = p[j]-p[i];
for(int k=0; k<=j; ++k) if(!in(ans, p[k])) {
double a2 = area2(pq, p[k]-p[i]);
Circle c = mCC(p[i], p[j], p[k]);
if(c.r<0) continue;
else if(a2 > 0 && (l.r<0||area2(pq, c.p-p[i]) > area2(pq, l.p-p[i]))) l = c;
else if(a2 < 0 && (r.r<0||area2(pq, c.p-p[i]) < area2(pq, r.p-p[i]))) r = c;
}
if(l.r<0&&r.r<0) c = ans;
else if(l.r<0) c = r;
else if(r.r<0) c = l;
else c = l.r<=r.r?l:r;
}
}
return c;
}
};