그룹 road to grandmaster 둘러보기
어느 ELO 레이팅이 안 그러겠냐만은, grandmaster라는 칭호는 세계적인 실력자에게 주어지는 칭호입니다. 가장 유명하고 세계적인 Competitive Programming(CP) 플랫폼인 Codeforces에서는 레이팅 2400 이상일 경우 grandmaster로 인정받으며, 닉네임이 붉은 색으로 변합니다. 한국 PS계에서는 이들을 ‘레드’라고 부르기도 합니다.
레드가 어느 정도 수치인지 대략적으로 가늠하자면, 2019년 5월 7일 기준으로 최근 6개월간 rated 대회를 친 사람 중 전 세계에 352명밖에 없습니다 (한국에선 16명). 국내 수준급의 프로그래밍 경시 대회의 대략적인 최소 입상 수준이 레이팅 1900-2100 (통칭 ‘퍼플’)이라는 점을 고려하면 단순히 닉네임에서 빛나는 붉은색의 간지를 넘어서 상당한 수준의 CP 능력 지니고 있다고 간주할 수 있습니다.
때문에 CP를 하는 수많은 프로그래머들에게 grandmaster라는 칭호는 원대한 꿈입니다. 6달 전부터 제공되기 시작한 문제별 난이도는 이 정도의 문제를 풀면 어느 수준의 레이팅에 이를 수 있다는 지표가 되었고, 높은 레이팅을 향하는 사람들에게 좋은 수치가 되었습니다.
Codeforces 사용자 hyunuk 님이 만든 road to grandmaster 라는 그룹도 이러한 취지에서 시작되었습니다. 난이도 분포를 유지하며 그룹 구성원의 누구도 풀지 않은 문제를 무작위로 선별하여 모의고사를 여는 시스템을 통해 다양한 종류의 문제를 접할 수 있게 되었습니다. 이번 포스팅을 통해 흥미로웠던 일부 문제에 대한 풀이를 작성해보고자 합니다.
1A. Ice cream coloring (CF 411 Div1C, 2200)
문제
$n$개의 정점으로 이루어진 트리에 다양한 종류의 아이스크림이 트리의 형태로 정점에 위치해있습니다. 이 때 같은 종류의 아이스크림은 같은 색으로, 같은 정점에 있는 서로 다른 종류의 아이스크림은 다른 색으로 하고자 할 때 필요한 최소 색깔의 수를 묻는 문제입니다.
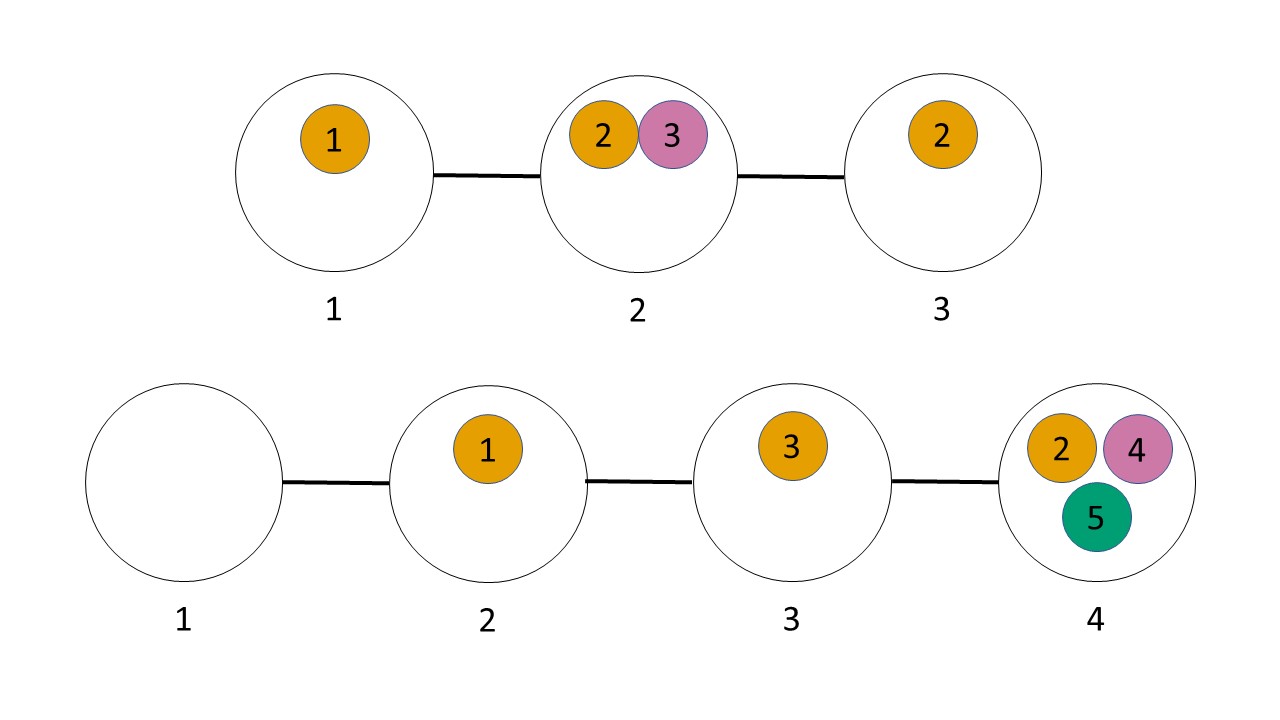
풀이
간단하면서도 강력한 dfs를 통해 최소 색깔의 수를 구할 수 있습니다. root부터 시작해, 각 정점의 아이스크림을 확인합니다.
- 만약 이미 색칠되어 있다면 ‘이 색은 이미 사용되었다’는 걸 체크하며, 아니면 따로 저장해놓습니다.
- 색칠이 안 된 아이스크림의 색깔을 간단히 1부터 대입해봅니다. 1이 이미 해당 정점에서 사용된 색깔이라면 2를 시도해보고…를 반복합니다.
- 언젠간 모든 아이스크림의 색깔을 결정할 수 있고, ‘이 색은 사용되었다’는 정보를 초기화하고 재귀적으로 반복합니다.
얼핏 생각하면 시간복잡도가 $O(NM)$은 될 것 같지만 이 방법은 $O(N+M)$에 작동합니다. 그 이유는 색칠이 안 된 아이스크림에 색을 배정하는 과정이 $O(s_i)$에 작동하기 때문입니다. 기존에 색칠되었던 아이스크림이 $x_i$개, 색칠되지 않은 아이스크림이 $y_i$개라고 하면 $1$부터 $x_i+y_i$의 수 중 사용되지 않은 수는 최소 $y_i$ 존재하게 되어, 새로 배정하는 색이 $s_i$ 이하가 됩니다.
색이 색칠되었는지 아닌지는 체크 배열을 이용해 사용 및 초기화를 $O(s_i)$에 수행할 수 있으므로 선형 복잡도가 완성됩니다.
실제 대회에서는 상당히 많은 system fail이 일어났습니다. 어떤 종류의 아이스크림이 전혀 등장하지 않아도 색깔은 배정해야 하는 테스트 케이스가 있는 것으로 보입니다 (예시 : 아이스크림이 3종류고, 모두 0개여도 필요한 최소의 색깔은 1개).
1K. New York Hotel (Testing Round 11B, 1900)
문제
택시기하계에서 집이 $C$개, 호텔이 $H$개 있습니다. 각 호텔에서 가장 멀리 떨어진 집과의 거리가 최소가 되는 호텔을 구하는 문제입니다. 수식으로 표현하자면 $(hx_i, hy_i)$를 $i$번째 호텔의 좌표, $(cx_j, cy_j)$를 $j$번째 집의 좌표라고 할 때
| $\min_i(\max_j( | hx_i - cx_j | + | hy_i - cy_j | ))$ |
을 최소로 하는 $i$를 구하는 것입니다.
풀이
좌표변환을 통해 45도 돌려서 생각하면 $|x-x’| + |y-y’| \leq k$가 $ max(x-x’, y-y’) <= k$로 바뀝니다. 좌표변환을 진행해도 얼핏 보면 모든 집의 좌표를 대입해봐야 할 것 같습니다. 그러나 $k$를 구하는 건 다음 문제로 환원할 수 있습니다.
”$(x,y)$를 중심으로 하는 정사각형이 모든 집(점)을 덮으려면 크기가 최소 얼마여야 할까?”
이렇게 생각하면 $x$좌표의 최대/최소값과 $y$좌표의 최대/최소값만 고려해도 된다는 점을 알 수 있습니다. 이를 통해 각 호텔마다 최소의 $k$를 $O(1)$에 구할 수 있습니다.
2A. Increase Sequence (CF 266 Div2D, 2300)
문제
길이 $n$의 정수 수열이 있습니다. 이 수열의 값을 모두 $h$로 동일하게 만들려고 하는데, 다음과 같은 규칙을 따라야 합니다
- 연속된 구간을 선택해서 해당하는 수열의 값에 1을 더할 수 있습니다.
- 이 선택된 구간들의 끝점은 서로 달라야 하며, 시작점도 서로 달라야 합니다.
위 조건을 만족하는 구간들의 집합의 개수$\mod 10^9 + 7$을 구하는 문제입니다.
풀이
각 항마다 이전 항과 다음 항과 비교를 진행하면 현재 위치에서 몇 개의 구간이 끝나며, 몇 개가 시작되어야 하는지를 알 수 있습니다. 2개 이상 시작되거나 끝나야 하는 칸이 있으면 불가능하므로 배제하겠습니다.
편의상 시작을 S, 끝을 E라고 하고, 스택처럼 S를 쌓아가봅시다. 왼쪽에서 오른쪽으로 훑으면서, 현재 있는 S의 개수를 $x$라고 하겠습니다.
E가 있으면, 지금까지 쌓아온S중 하나와 매칭을 시킬 수 있기에 현재까지 구한 답에 $x$를 곱하면 됩니다. 그리고 $x$를 1 감소시킵니다.E가 없고 다음 칸에S가 추가되지 않는다면 현재 칸에는E를, 다음 칸에는S를 추가하면서 구간을 나누는 선택지가 추가됩니다. 나눌 경우 구간을 나누지 않고 이대로 진행하는 1가지 방법에 구간을 나누는 $x$가지의 방법이 추가되므로 $(x+1)$을 곱하면 됩니다.
이 풀이는 시간복잡도/공간복잡도 $O(N)$이지만 $O(N^2)$ 동적 계획법을 사용하는 방법도 있으며, 기본적으로는 이 풀이와 비슷합니다.
2C. Giving Awards (Coder-Strike 2014 - Round 1 D, 1900)
문제
임의의 두 정점 $u$와 $v$에 대해 $(u, v)$나 $(v, u)$가 연결되어 있는 방향그래프가 있습니다. 이 그래프에 아무 오일러 경로, 즉 한 점에서 시작해 모든 점을 단 한 번씩만 방문하는 경로가 존재하면 출력하는 문제입니다.
풀이
주어진 그래프에서 오일러 경로는 항상 존재합니다. 보다 정확히 말하면, 임의의 서로 다른 두 정점이 단방향으로 연결된 tournament graph에서 오일러 경로가 존재합니다.
만드는 방법은 생각보다 간단합니다. 수학적 귀납법을 통해 길이 $n$의 경로가 만들어져 있으면 항상 길이 $n+1$의 경로를 만들 수 있음을 보일 수 있습니다. 즉, 반드시 정점을 처음이나 중간이나 끝에 끼워넣을 수 있으므로 이를 그대로 구현하면 됩니다.
놀랍게도 ‘삽입해가면서 만들어가기’가 충분한 시간 복잡도를 가지고 있습니다. 정점을 1번부터 $n$번까지 추가하되, 이진 검색 트리 등을 이용해 $ x \to i $ 나 $ i \to x$가 가능한지 아닌지 $O(\lg n)$에 확인할 수 있습니다. 한 번 확인된 ‘연결 불가능한 간선’은 각 정점에 따라 최대 2번 확인되고 그 외에는 항상 추가할 수 있으므로 총 복잡도 $O(n \lg n)$에 경로를 만들 수 있습니다.
구현엔 여러 방법이 있겠지만 오랜만에 쓴 C++의 list가 직관적이었습니다.
3A. Jzzhu and Numbers (CF 257 Div1D, 2400)
문제
$0 \leq a_i \leq 10^6$이고 $1 \leq i \leq n \leq 10^6$일 때, bitwise and해서 0이 되는 공집합이 아닌 부분집합의 개수를 구하는 문제입니다.
풀이
우선 포함배제의 원리를 통해 $g(i)$를 $i$을 2진수로 나타냈을 때 1의 개수, $f(i)$ 를 $a_j \ \&\ i = i$인 $a_j$의 개수라고 하면 답이 $\sum\limits_i (-1)^{g(i)} 2^{f(i)}$임을 알 수 있습니다 (문제의 의미를 따지면 $2^{f(i)}-1$이 맞으나, 이항정리에 의해 값은 동일합니다). 그럼 $f(i)$를 어떻게 빠르게 구할 수 있을까요?
어떤 수 $x$랑 $i$랑 bitwise and를 해서 $i$가 나온다는 뜻은, $i$를 2진수로 나타냈을 때 1인 비트는 $x$도 1이나 0인 비트는 어느 값이나 가질 수 있다는 것을 의미합니다. $f’(i)$를 수열에 있는 $i$의 개수라고 하면 3비트 체계에서는 $f(2) = f’(2) + f’(3) + f’(6) + f’(7)$이 됩니다.
Fenwick tree를 구축할 때 사용하는 원리를 이용하면 $O(n \lg \max a_i)$에 구축할 수 있습니다. 그림을 보면 어떤 형태인지 이해가 될 것 같습니다.
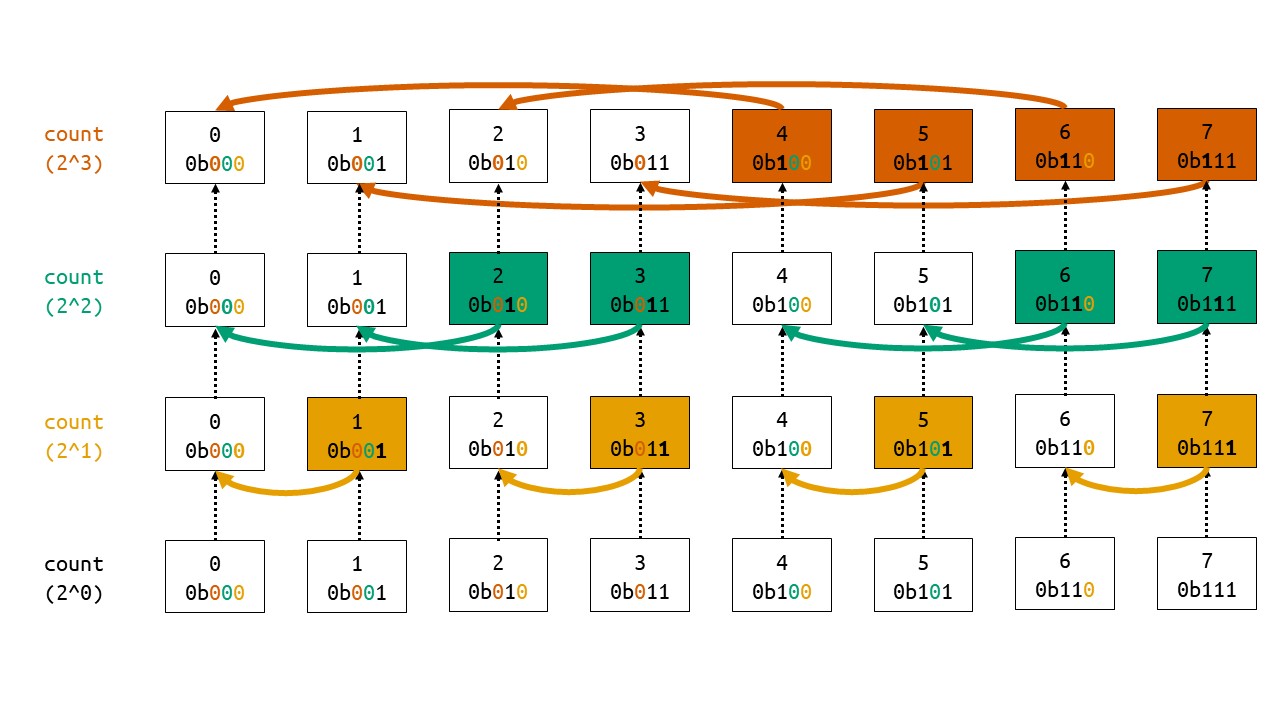
비트를 하나씩 보면서 1이 있는 수를 0인 수쪽에 합쳐서 계산하는 과정을 반복하면 되고, 코드도 놀랍도록 간결합니다.
3D. Almost Permutation (CF Edu 29 F, 2300)
문제
$1$ 이상 $n$ 이하의 수로만 이루어진 수열을 다음과 같은 조건을 만족하며 만들어야 합니다.
- 일부 구간의 수는 $x_i$ 이상입니다.
- 일부 구간의 수는 $x_i$ 이하입니다.
- $cnt(i)$를 수열에 $i$가 나타나는 횟수라고 정의할 때, $\sum\limits_i cnt(i)^2$를 최소화해야 합니다.
만들 수 있다면 $\sum\limits_i cnt(i)^2$의 최소값을 구하는 문제입니다.
풀이
위치와 값이 최소의 비용으로 매칭이 되어야 하는 것이므로 Min-cost Max-flow Algorithm을 사용하면 됩니다. 그래프 구축 방법은 다음과 같습니다.
- source 정점이 $0$번, sink 정점이 $2n+1$번입니다.
- $ 1 \leq i \leq n$일 때 source에서 $i$로 가는 용량 $1$, 비용 $0$의 간선을 만듭니다.
- $x$번째 수로 $y$가 가능하면 $x$에서 $n+y$로 용량 $1$, 비용 $0$의 간선을 만들어줍니다.
- $ 1 \leq i \leq n$일 때 $n+i$에서 까지 sink로 용량 $1$, 비용 $1, 3, 5, …, 2n-1$의 각각 $n$개의 간선을 만들어줍니다. 이는 $cnt$값을 계산하기 위함입니다.
총 간선은 $O(n^2)$, 총 정점은 $O(n)$, 최대 유량은 $n$으로 SPFA를 이용하면 $O(n^4)$의 시간 복잡도로 min-cost를 구할 수 있습니다. max-flow가 $n$일 때 min-cost가 정답이 됩니다.
3K. Police Patrol (CF 244 Div2E, 2000)
문제
경찰관들이 경찰차를 타며 체포해야 하는 용의자들의 $x$좌표 위치가 오름차순으로 주어집니다. 경찰차에 최대 $k$명의 용의자들을 태울 수 있다 할 때, 경찰서를 어디에 지어야 모든 용의자를 최소의 거리를 이용해서 경찰서로 옮길 수 있는지 묻는 문제입니다.
풀이
경찰서는 용의자가 있는 위치에 세우는 것이 최적입니다. 그러므로 위치의 후보가 $n$개로 줄어듭니다. 그럼 경찰차가 언제 U턴해야 하는지 따져볼 수 있습니다. 용의자가 8명 있고 최대 3명 태울 수 있을 때 경찰서의 위치를 $, 유턴해야 하는 위치를 o라고 하면
$o..o..o
o$..o..o
o.$.o..o
o..$o..o
o..o$..o
o..o.$.o
o..o..$o
o..o..o$
의 모양을 보입니다. 왼쪽과 오른쪽을 따로 보면 일관된 모습을 보인다는 점을 알 수 있고 prefix sum을 통해 각 방향에서의 거리를 구할 수 있습니다.
3L. Sonya and Matrix (CF 495 Div2D, 2200)
문제
$(x, y)$에 0을 쓰고, 나머지 칸에 $(x, y)$과의 거리를 써놓은 $ n \times m $ 격자를 생각해봅시다. 이 격자에 있는 숫자들만 주어졌을 때 $n, m, x, y$를 복원할 수 있을까요?
풀이
$n, m, x, y$가 주어졌을 때 격자에 쓰여진 수의 총합을 계산할 수 있습니다.
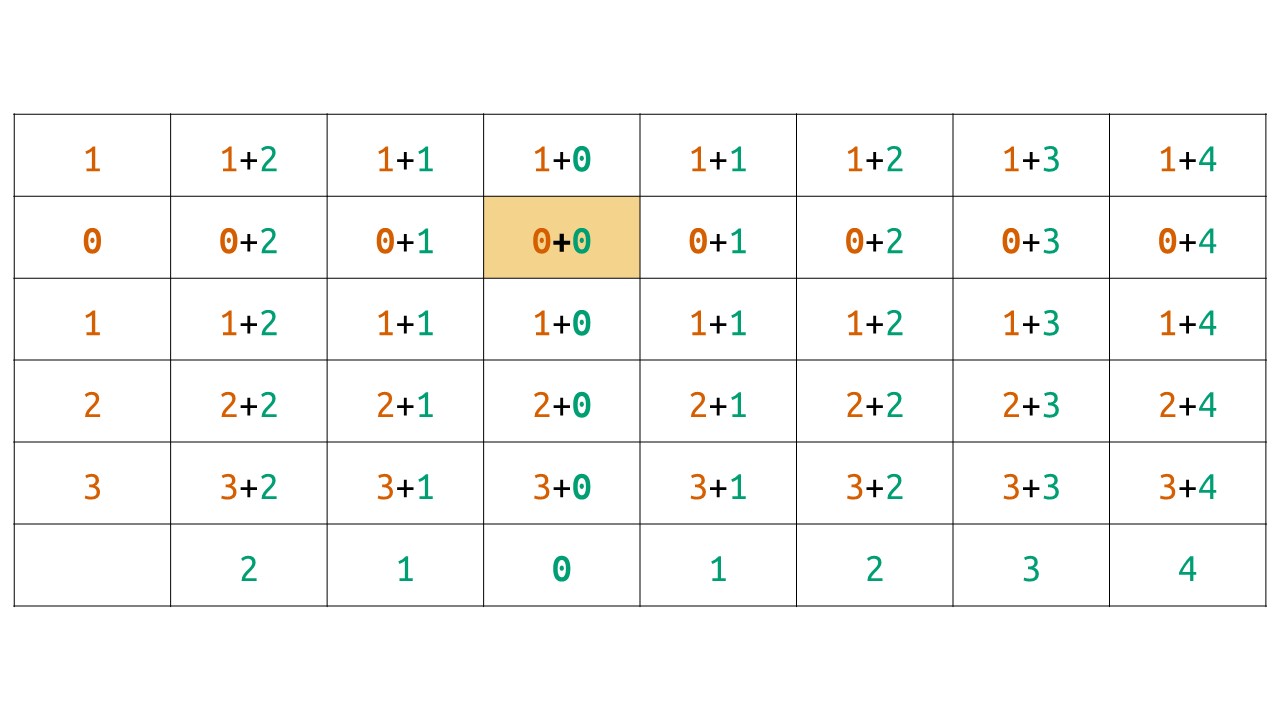
그림과 같이 행과 열을 따로 분리해서 생각하면 합이 $ m(\binom{x}{2} + \binom{n-x+1}{2}) + n(\binom{y}{2} + \binom{m-y+1}{2})$라는 것을 도출해낼 수 있습니다. 다행히 합이 같으면서 $n, m, x, y$가 다른 경우가 그리 흔하지가 않습니다. 그렇기에 $t= nm$을 소인수분해해 모든 가능한 $(x, y)$쌍에 대해 합이 일치하는지 확인하고 원소를 비교하는 방식으로 알고리즘을 작성할 수 있습니다. 필수적인지는 모르겠지만 적당한 커팅 (이론치 최대값 비교 등)을 사용하면 여유롭게 시간 제한을 통과할 수 있습니다.
결론
문제를 모두 소개하진 않았지만, Codeforces의 문제 레이팅이 전부가 아니라는 사실을 알 수 있었습니다. 특히 옛날 문제는 난이도에 비해 레이팅이 낮게 잡히는 경우가 많았으며, 팀대회나 이벤트성 특수 대회도 레이팅 계산은 일괄적으로 진행되다보니 함정 문제들이 되곤 했습니다.
코드포스 레이팅이 전부는 아니지만, 코드포스 레이팅을 올리고 싶다면 결국 코드포스 문제를 풀어야 합니다. 대회 하나를 잡고 푸는 것도 방법일 수 있지만, 난이도 편차가 크기 때문에 어려울 수 있습니다. 난이도를 잡고 풀 수도 있지만, 난이도를 맹신하면 안 됩니다. road to grandmaster는 다양한 수준의 문제가 나오고 문제를 푼 사람과 토의도 진행해볼수 있다보니 좋은 환경이었고, 다양한 방면의 문제를 접할 수 있어서 좋았습니다. 실력은 키우고 싶은데 무슨 문제를 풀어야 할지 모르겠다면 road to grandmaster에 들어와보시길 바랍니다.
다시 한 번 road to grandmaster 그룹을 만들어주신 hyunuk 님에게 감사를 표합니다. gl hf!