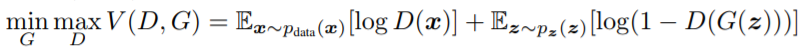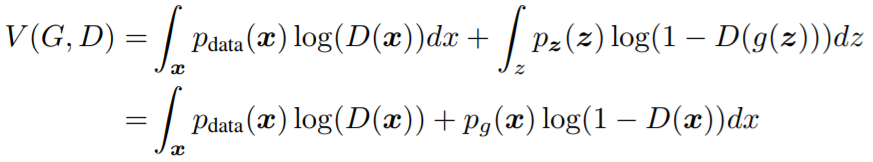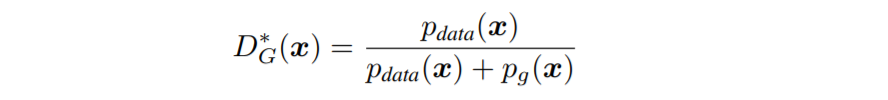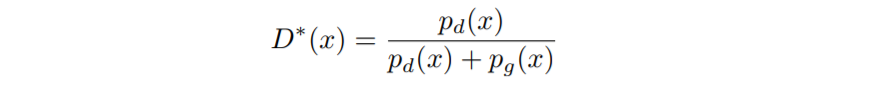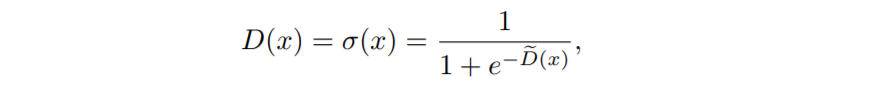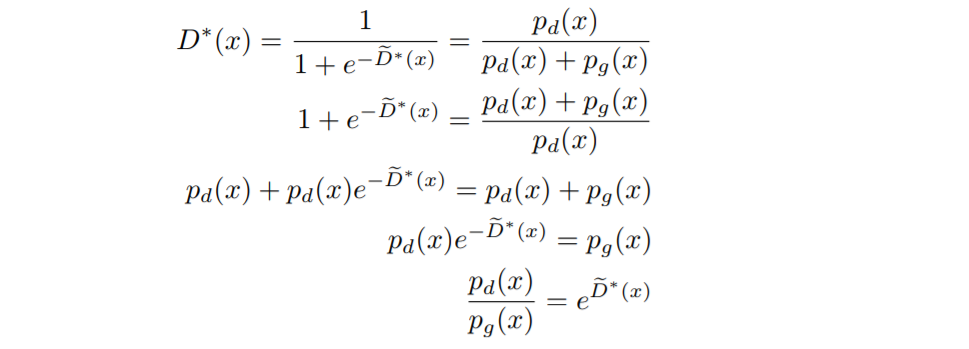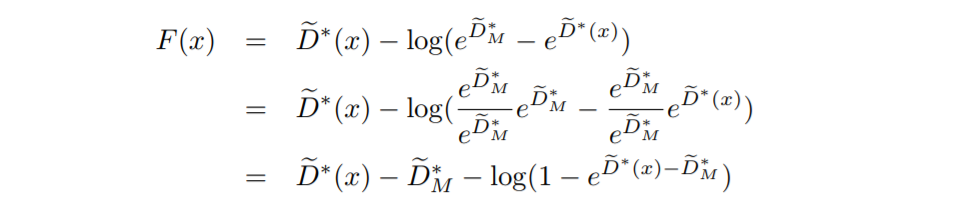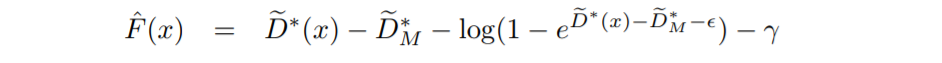Discriminator Rejection Sampling
generative-adversarial-networks , rejection-sampling , discriminator-rejection-sampling
Generative Adversarial Networks(GANs)는 머신러닝 기술의 일종으로 생성자(generator)와 판별자(discriminator) 두 네트워크를 적대적으로 경쟁시켜 학습시키는 프레임워크를 말합니다. 보통 GANs에서는 학습이 완료되면 생성자 네트워크만 사용하고 판별자 네트워크는 버리게 됩니다. 하지만, 학습 이후에 여전히 생성자 네트워크가 실제 데이터 분포를 완벽히 묘사하지 못하고 판별자 네트워크가 이에 대해 중요한 정보를 가지고 있을 수도 있습니다. 그렇다면 학습 이후에도 판별자 네트워크를 활용하여 생성자 네트워크의 성능을 높일 수 있지 않을까요?
Discriminator Rejection Sampling(DRS)은 ICLR 2019에 accept된 논문으로 GANs 학습 이후에 판별자(discriminator)를 이용하여 생성자(generator)의 성능을 향상시키는 방법을 소개하고 있습니다. 판별자가 가진 정보를 바탕으로 생성자의 샘플로부터 rejection sampling을 진행해서 실제 데이터 분포와 비슷한 샘플을 얻는 것이 주요 아이디어입니다.
이번 포스트에서는 DRS의 핵심 아이디어를 소개해보겠습니다. 이 논문을 이해하기 위해서는 GANs에 대한 사전 지식이 필요합니다. 하지만, GANs에 대해서는 이미 잘 설명한 글이 많기 때문에 깊게 다루지 않겠습니다.
Generative Adversarial Networks
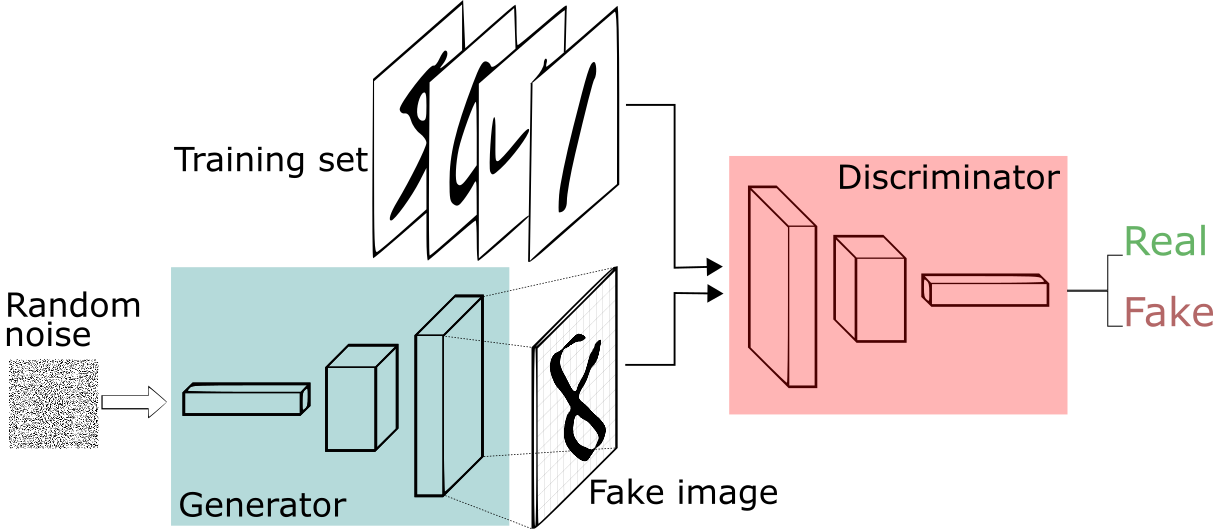
Generative Adversarial Networks(GANs)는 생성자(generator)와 판별자(discriminator) 두 뉴럴 네트워크로 구성되어 있습니다. 이름에서 알 수 있듯이 두 네트워크는 서로 적대적으로 경쟁하여 학습을 진행합니다. 생성자 $G$는 판별자 $D$를 속이기 위해 원래의 데이터와 최대한 비슷한 데이터를 만들도록 학습합니다. 반대로 판별자 $D$는 원래의 데이터와 생성자 $G$가 만드는 데이터를 잘 구분하도록 학습이 진행됩니다.
위 그림에서 noise 값을 $z$라 하고 분포 $p_z(z)$를 따른다고 합시다. 그러면 생성자 $G$는 파라매터 $\theta_g$의 뉴럴 네트워크로 표현된 미분 가능한 함수 $G(z;\theta_g)$로 나타낼 수 있습니다. 마찬가지로 실제 데이터 $x$가 분포 $p_{data}(x)$를 따른다고 하면 판별자 $D$를 파라매터 $\theta_d$의 뉴럴 네트워크로 표현된 미분 가능한 함수 $D(x;\theta_d)$로 나타낼 수 있습니다. 이때 $D(x)$는 $x$가 생성자가 아닌 실제 데이터에서 왔을 확률을 가리킵니다.
그래서 $D$는 $D(x)$에서 $x$가 실제 데이터이면 높은 값을, 가짜 데이터이면 낮은 값을 부여하도록 학습하게 됩니다. 반대로 $G$는 이를 방해하는 방향으로 학습이 진행됩니다. 이를 간단히 수식으로 표현하면, 학습은 다음과 같은 식 $V(D,G)$를 두고 $D$와 $G$가 minmax 게임을 진행하는 것과 같다고 할 수 있습니다.
DRS를 이해하기 위해서는 최적 판별자(optimal discriminator)에 대해 알아둘 필요가 있습니다. 최적 판별자 $D_G^\ast(x)$는 생산자를 고정시켰을 때 $V(D,G)$를 최대화시키는 $D(x)$로 정의됩니다. $D_G^\ast(x)$를 구하기 위해 $V(D,G)$를 다음과 같이 표현해봅시다.
$(a,b)\in \mathbb{R}^2{\backslash}{(0,0)}$일 때, $(0,1)$에서 정의된 함수 $y=a\log(x) + b\log(1-x)$는 $x = {a\over{a+b}}$에서 최댓값을 가집니다. 또한, 위 식에서 $p_{data}(x)$나 $p_g(x)$가 0이 되는 $x$는 고려하지 않아도 되므로 $D_G^\ast(x)$는 다음과 같게 됩니다.
이처럼 $D_G^\ast(x)$는 $p_{data}(x)$와 $p_g(x)$ 두 분포로 간단히 나타나게 됩니다. 후에 자세히 설명하겠지만, 이 식은 GANs에서 rejection sampling을 할 수 있게 하는 핵심적인 역할을 하게 됩니다.
Rejection Sampling
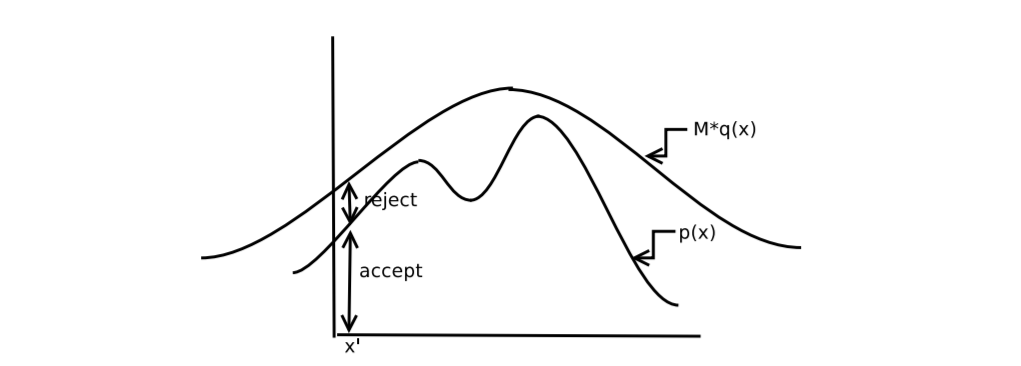
rejection sampling은 주어진 확률 분포의 확률 밀도 함수는 알고 있지만 직접 샘플링하기 어려울 때 사용할 수 있는 방법입니다. 샘플링하고 싶은 분포가 $p$라고 했을 때, rejection sampling을 하기 위해서는 먼저 샘플링 하기 쉬운 제안 분포(proposal dsitribution) $q$를 잡아야 합니다. 그 다음에는 모든 $x$에 대해 $p(x) \leq Mq(x)$가 성립하는 상수 M을 잡아야 합니다.
그러면 $p$와 $q$ 두 분포는 다음과 같은 그림으로 표현할 수 있습니다.
$p$에서 샘플을 얻기 위해서는 최소한 두 번의 샘플링 과정이 필요합니다. 먼저, $q(x)$에서 샘플 $x$를 얻습니다. 그 다음에는 $[0,1]$ 구간의 uniform distribution에서 샘플 $u$를 얻습니다. 여기서 $u$가 acceptance probability인 $p(x)\over Mq(x)$보다 작다면 $x$를 $p$의 샘플로 accept하고 그렇지 않다면 reject합니다. 이 과정을 의사코드로 나타내면 다음과 같습니다.
직관적으로 샘플이 accept될 확률은 위 그림에서 $p$ 아래 부분 넓이에서 $Mq$ 아래 부분 넓이를 나눈 것과 같으므로 $1\over M$이 됩니다. 혹은 다음과 같이 수식으로 구할 수 있습니다.
\[\begin{aligned} \mathbb{P}(X accepted) &= \mathbb{P}\left(U\leq{p(X) \over Mq(X)}\right) \\ &= \int\mathbb{P}\left(U\leq{p(X) \over Mq(X)} \bigg| X=x\right)q(x)dx \\ &= \int {p(x) \over Mq(x)}q(x)dx \\ &= {1\over M} \end{aligned}\]그러면 샘플이 accept되었을 때 $x$에서 샘플되었을 확률은
\[\begin{aligned} \mathbb{P}(X=x|X accepted) &= {\mathbb{P}\left(U\leq{p(X) \over Mq(X)}\bigg | X=x \right)q(x)\over \mathbb{P}(X accepted)} \\ &= {p(x) \over Mq(x)}q(x) \cdot M \\ &= p(x) \end{aligned}\]따라서 위 알고리즘에서 accept된 샘플을 얻는 것과 $p$에서 샘플링을 하는 것은 동일합니다. 위 식에서 채택률은 $M$에 반비례하게 된다는 점을 알 수 있습니다. 그러므로 rejection sampling을 효율적으로 하기 위해서는 제안 분포를 $p$와 비슷하게 설정해서 $M$을 최소화해야 합니다.
Discriminator Rejection Sampling
GANs를 학습하고 나면 이론적으로는 생성자가 만드는 데이터와 실제 데이터는 구분할 수 없게 되어야 합니다.(즉, D(x)는 항상 $1\over 2$를 내놓아야 합니다.) 그래서 GANs을 학습하고 나면 판별자는 더이상 필요가 없어지고 생성자만 사용하게 될 것입니다. 하지만, 현실에서 이 가정은 성립하지 않고 학습 이후에 판별자가 내놓는 값도 항상 $1 \over 2$이 되지는 않습니다. 따라서 판별자는 여전히 실제 데이터에 대해 생성자가 가지지 못한 정보를 가지고 있다고 볼 수 있습니다. 학습 이후에도 판별자를 통해 이 정보를 활용하면 생성자를 더 발전시킬 수 있을 것입니다. 여기에서 DRS는 판별자로 생성자의 샘플로부터 rejection sampling을 해서 더 나은 샘플을 얻는 방법을 제시합니다.
$p_d(=p_{data})$를 우리가 구하고자 하는 실제 데이터의 분포라고 합시다. 그리고 $p_g$와 $p_d$의 support가 같다고 가정합니다.(즉, $p_g(x)\neq 0 \iff p_d(x)\neq 0$) rejection sampling을 하기 위해서는 제안 분포와 위에서 설명한 상수 $M$이 필요합니다. 제안 분포는 생성자의 분포인 $p_g$로 놓고 $M$은 $\max_x p_d(x)/p_g(x)$으로 놓습니다. 그런데 $p_d(x)$와 $p_g(x)$ 모두 implicit하게 정의된 분포이기 때문에 값을 정확히 알 수 없습니다. 그렇다면 acceptance probability인 $p_d(x)/Mp_g(x)$ 값은 어떻게 구할까요?
위에서 구한 최적 판별자 $D^\ast(=D_g^\ast)$에 관한 식에 주목합시다.
그리고 다음과 같이 로지스틱 함수를 사용해서 판별자를 정의합시다.
그러면 다음과 같이 $D^\ast(x)$로 $p_d(x)/p_g(x)$를 표현할 수 있습니다.
$x^\ast$를 $p_d(x)/p_g(x)$를 최대화하는 $x$ 값이라고 하면 $M=e^{\tilde D^\ast(x^\ast)}$이 됩니다. 편의상 $\tilde D^\ast_M:=\tilde D^\ast(x^\ast)$로 표기하면 acceptance probability는 $e^{\tilde D^\ast(x)-\tilde D^\ast_M}\in[0,1]$가 됩니다. 결과적으로 rejection sampling를 하기 위해 $D^\ast$와 $M$을 알아야 합니다.
논문에서는 위에서 분석한 결과가 다음과 같은 현실적인 문제를 가지고 있다고 합니다.
- 실제로 확률 밀도 함수를 최적화할 수 없으므로 $D^\ast$를 구할 수 없습니다. 또한, acceptance probability가 $p_d(x)/p_g(x)$에 비례할 필요가 없습니다.
- 큰 데이터셋에서 $p_g$와 $p_d$의 support가 같지 않습니다. 만약 $p_g$와 $p_d$의 support intersection이 작을 경우, 많은 구역에서 $p_d(x)/p_g(x)$를 단순히 0으로 놓게 될 것입니다.
- 실제로 $p_d$에서 무한히 샘플링을 할 수 없습니다. 만약 $D$를 유한한 양의 데이터로 최적화하면 학습하지 않은 지점에서 0이 아닌 값을 내놓을 것입니다.
- 실제로 $M$을 정확하게 구할 수 없습니다.
- rejection sampling은 target distribution이 고차원일 때 acceptance probability가 매우 낮게 나오는 경향이 있습니다.
이를 해결하기 위해 논문에서는 $D^\ast$와 $M$을 적당한 방법으로 근사하고 있습니다. GANs에서 학습시킨 $D$가 좋은 샘플과 나쁜 샘플을 잘 구분할 것이라고 가정하고 이를 $D^\ast$로 놓습니다. 그리고 $M$을 처음에 많은 수(실험에서는 10000번)의 샘플링을 해서 구한 $e^{\tilde D^\ast(x)}$의 최댓값으로 근사하고 이후 샘플링을 할 때마다 최댓값으로 갱신하여 사용했습니다.
이 때, 5번 문제 때문에 DRS에서는 샘플링을 계속하다가 acceptance probability가 매우 낮아질 수 있습니다. $\tilde D^\ast_M$의 값이 너무 크면 acceptance probability인 $e^{\tilde D^\ast(x)-\tilde D^\ast_M}$가 작아져서 대부분의 샘플이 reject되는 문제가 발생하기 때문입니다. 이를 해결하기 위해 논문에서는 다음과 같이 새로운 함수 $F(x)$를 정의하였습니다.
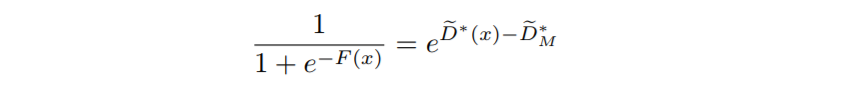
그리고 실제로는 $F(x)$ 대신에 다음과 같이 정의된 $\hat F(x)$를 사용하여 acceptance probability를 구했습니다.
여기서 $\epsilon$은 계산의 안정성을 위해 도입한 작은 상수이고 $\gamma$는 acceptance probability 정도를 조절할 수 있게 하는 hyperparmeter입니다. $\gamma$가 양의 방향으로 커지면 대부분의 샘플이 reject되고 음의 방향으로 커지면 대부분의 샘플이 accept되게 됩니다.
다음은 DRS의 의사코드입니다.
아래는 실제 데이터가 25점의 2D-Gaussian Distribution에서 샘플링 될 때 일반 GANs와 DRS의 성능 차이를 분석한 실험 결과입니다. DRS를 통해 GANs의 성능이 크게 좋아졌음을 알 수 있습니다.

관련 연구
Bayesian Deep Learning NIPS 2018 Workshop에서는 비슷한 아이디어로 Metropolis-Hastings algorithm을 사용하여 성능을 높인 Metropolis-Hastings GAN이 소개되었습니다.(Discriminator Rejection Sampling이 먼저 제안되었습니다.) Metropolis-Hastings algorithm를 사용해서 rejection sampling에서 생기는 단점들을 다소 극복한 것 같습니다. DRS와의 비교에서 더 나은 성능을 내고 있다고 주장하고 있습니다.
참고문헌
- Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio (2014). “Generative Adversarial Nets”
- Samaneh Azadi, Catherine Olsson, Trevor Darrell, Ian Goodfellow, Augustus Odena (2019). “Discriminator Rejection Sampling”
- https://people.eecs.berkeley.edu/~jordan/courses/260-spring10/lectures/lecture17.pdf