이산 로그(Dicrete Logarithm)
이산 로그란?
수학에서의 로그는 모두 익숙할 것입니다. $a^x = b$일 때 $x = log_a b$입니다. 실수에서는 $a, b$가 주어졌을 때 $a^x = b$를 만족하는 $x$, 즉 $log_a b$를 아주 간단하게 계산할 수 있습니다. 그러나 $Z_p$에서는 이를 계산하는 것이 간단하지 않습니다. 이와 같이 $Z_p$에서 주어진 $a, b$에 대해 $a^x = b$를 만족하는 $x$를 찾는 문제가 바로 이산 로그(Discrete Logarithm) 문제입니다. 이산 로그 문제에서 $p$는 소수, $a$는 $p$의 원시근인 것이 좋습니다. $a$가 $p$의 원시근이라면 $a^0, a^1, a^2, \dots a^{p-1}$가 모두 다르기 때문입니다. 반대로 말해, $a$가 $p$의 원시근이 아니라면 $a^0, a^1, a^2, \dots a^{p-1}$ 중에 중복되는 것이 존재합니다.
아직까지 이산 로그 문제에 대한 효율적인 계산법은 나오지 않았습니다.(여기서 효율적인 계산법이라고 하는 것은 $p=2^n$일 때 $n$에 대한 다항 시간에 계산할 수 있는 계산법을 의미합니다.) 참고로 이산 로그 문제는 NP-complete에 속하는 문제는 아니기에 효율적인 계산법이 나올 가능성은 충분히 있습니다. 또한 Quantum Computer에서는 P에 속함이 증명되어 있습니다. Shor’s algorithm Link
이산 로그는 Elgamal Encryption, Diffie-Hellman 키 교환, Digital Siganature Algorithm 등과 같이 암호화, 키 교환, 인증 등의 각종 암호 분야에서 쓰이고 있습니다. 만약 이산 로그 문제가 효율적으로 풀리게 된다면 위에서 언급한 암호 시스템이 안전하지 않게 됩니다. 또한, 비록 일반적인 이산 로그에 대한 풀이법 자체는 아직 찾지 못했다고 하더라도 $a, b, p$를 적절하게 택하지 못하는 구현의 실수로 인해 기밀성이 지켜지지 않는 경우도 있습니다. 이번 글에서는 이산 로그의 다양한 풀이법을 살펴보고 어떻게 하면 안전하게 이산 로그를 사용할 수 있는지 알아보겠습니다.
풀이법1 - 전수 조사
이 풀이법은 가장 떠올리기 쉽고 구현도 간단한 풀이법입니다. 바로 $x$에 0부터 $p-1$까지 차례로 넣어보며 $a^x = b$를 만족하는 $x$를 찾는 것입니다.
def func(a, b, p):
val = 1
for x in range(p):
if val == b: return x
val = val*a % p
return -1
아쉽게도 이 방식은 최악의 경우 $p$번의 곱셈이, 평균적으로는 $p/2$번의 곱셈이 필요하기 때문에 $p$가 1024-bit 혹은 2048-bit인 보통의 경우에는 현실적인 시간 내에 풀이가 불가능합니다.
풀이법2 - Baby-step giant-step Algorithm
두 번째로 살펴볼 방법은 아기걸음 거인걸음이라는 아주 귀여운 이름이 붙어있는 알고리즘입니다. 알고리즘의 이름은 생소할 수 있지만 일종의 MITM(Meet In The Middle) 알고리즘으로, 이 알고리즘을 통해 시간복잡도를 $O(p)$에서 $O(p^{0.5})$로 떨굴 수 있습니다.
편의상 $k = \lfloor p^{0.5} \rfloor$ 라고 합시다. 이 때 $a^x = b$를 만족하는 $x$는 $nk+m$꼴로 나타낼 수 있습니다. $a^{nk+m} = b$는 $a^{nk} = a^{m-1}b$로 변형이 가능하므로 $a^{nk} = a^{0}, a^{k}, a^{2k}, a^{3k}, \dots$에 대한 테이블을 만들고 $a^{-m}b = a^{-0}b, a^{-1}b, a^{-2}b, \dots$에 대한 테이블을 만들어 값이 일치하는 원소를 찾으면 됩니다.
해쉬를 이용할 경우 $O(p^{0.5})$, 정렬을 이용할 경우 $O(p^{0.5}lgp)$에 이산 로그 문제를 해결할 수 있습니다. 정렬을 이용한 예시 코드는 아래와 같습니다.
def egcd(a1, a2):
x1, x2 = 1, 0
y1, y2 = 0, 1
while a2:
q = a1 // a2
a1, a2 = a2, a1 - q * a2
x1, x2 = x2, x1 - q * x2
y1, y2 = y2, y1 - q * y2
return (x1, y1, a1)
def inv(a, m):
x, y,g = egcd(a, m)
if g != 1:
raise Exception('No modular inverse')
return x%m
def func2(a, b, p):
table1 = []
k = int(p**0.5)
val = 1
mul = pow(a,k,p)
for i in range(0,p,k):
table1.append((val, i//k))
val = val * mul % p
table2 = []
ainv = inv(a,p)
val = b
for i in range(k):
table2.append((val, i))
val = val * ainv % p
table1.sort()
table2.sort()
idx1 = 0
idx2 = 0
while idx1 < len(table1) and idx2 < len(table2):
if table1[idx1][0] < table2[idx2][0]:
idx1 += 1
elif table1[idx1][0] > table2[idx2][0]:
idx2 += 1
else:
return k*table1[idx1][1]+table2[idx2][1]
return -1
풀이법3 - Pollard’s rho Algorithm
Pollard’s rho Algorithm은 $a^{n_1}b^{m_1} = a^{n_2}b^{m_2}$인 적절한 $n_1, n_2, m_1, m_2$를 찾았을 때 $log_ab = (n_2-n_1)(m_1-m_2)^{-1}$이라는 점을 이용하는 알고리즘입니다. 이 알고리즘의 시간복잡도는 $O(p^{0.5})$입니다. 같은 시간복잡도를 가지는 Baby-step giant-step Algorithm과 비교할 때 이 알고리즘은 확률적 알고리즘이기 때문에 $O(p^{0.5})$에 반드시 답이 찾아짐을 보장할 수 없고 상수가 약간 크다는 단점이 있지만, 공간을 $O(1)$만 사용한다는 아주 큰 장점이 있습니다.
이 알고리즘은 임의의 $a^{n}b^{m}$ 꼴의 수들로 수열을 만들었을 때 해당 수열에서 cycle을 찾아내는 방식으로 동작합니다. 수열에서의 cycle은 Floyd’s cycle-finding algorithm으로 구할 수 있습니다. 알고리즘에 대해 간략하게 설명을 하자면, 한 번에 한 칸씩 가는 거북이와 두 칸씩 가는 토끼를 수열 상에서 이동시켜 거북이와 토끼가 같은 값에 위치하는 순간을 찾는 방법입니다.
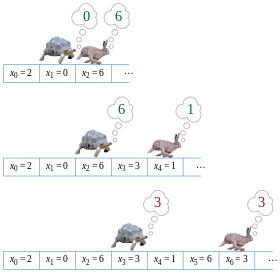
$f(x) = a^{n}b^{m}$ 꼴의 수열을 만들기 위해 $x$를 3으로 나눈 나머지에 따라 각각 $f(x+1) = ax$ 혹은 $f(x+1) = bx$ 혹은 $f(x+1) = x^k$으로 계산합니다. 반드시 $ax, bx, x^k$일 필요는 없고 $a^2x, b^2x, ab^2x^4$등과 같이 $f(x+1)$이 여전히 $a^{n}b^{m}$ 꼴이 되게끔 하는 수라면 어떤 것이어도 무관합니다. 그리고 초기 항은 $a^0b^0$으로 잡아도 무관하고, 임의의 $n, m$에 대해 $a^nb^m$으로 잡아도 무관합니다.
그 후 $f(x)$에 대해 앞에서 소개한 Floyd’s cycle-finding algorithm 으로 $a^{n_1}b^{m_1} = a^{n_2}b^{m_2}$를 만족하는 $n_1, n_2, m_1, m_2$를 찾습니다. 만약 $m_1 = m_2$일 경우에는 탐색에 실패한 것이므로 다른 초기항을 잡아 같은 절차를 반복합니다. 예시 코드는 아래와 같습니다.
def egcd(a1, a2):
x1, x2 = 1, 0
y1, y2 = 0, 1
while a2:
q = a1 // a2
a1, a2 = a2, a1 - q * a2
x1, x2 = x2, x1 - q * x2
y1, y2 = y2, y1 - q * y2
return (x1, y1, a1)
def inv(a, m):
x, y,g = egcd(a, m)
if g != 1:
raise Exception('No modular inverse')
return x%m
def nxt(x, n, m, a, b, p):
if x % 3 == 0:
x = a*x%p
n = (n+1)%(p-1)
elif x % 3 == 1:
x = b*x%p
m = (m+1)%(p-1)
else:
x = x*x*x%p
n = 3*n%(p-1)
m = 3*m%(p-1)
return x,n,m
def cycle_detection(a, b, p):
nrandom = random.randint(0,p-2)
mrandom = random.randint(0,p-2)
x_calc = pow(a, nrandom, p)*pow(b,mrandom,p)%p
x1, n1, m1 = x_calc, nrandom, mrandom
x2, n2, m2 = x_calc, nrandom, mrandom
while(True):
x1, n1, m1 = nxt(x1, n1, m1, a, b, p)
x2, n2, m2 = nxt(x2, n2, m2, a, b, p)
x2, n2, m2 = nxt(x2, n2, m2, a, b, p)
if x1 == x2:
try:
return (n2-n1)*inv(m1-m2, p-1)%(p-1)
except:
return -1
def func3(a, b, p):
while True:
ret = cycle_detection(a,b,p)
if ret != -1: return ret
그런데 이 방식 자체는 문제가 없으나 실제로 임의의 $a, b, p$에 대해 해당 함수를 실행해보면 cycle_detection 함수에서 $m_1-m_2$가 $p-1$과 서로소가 아니어서 inverse가 구해지지 않는 경우가 비일비재합니다. 이를 해결하기 위해 $p-1$을 소인수분해 한 후 각 소인수에 대해 주기를 계산하는 절차가 추가된다면 효율적일 것입니다.
풀이법4 - Pohlig-Hellman Algorithm
Pohlig-Hellman Algorithm은 위에서 언급한 것과 같이 $p-1$의 소인수에 대해 주기를 계산하는 알고리즘으로, $p-1$이 작은 소인수의 곱으로 나타낼 수 있을 때에는 큰 $p$에 대해서도 현실적인 시간 내에 계산이 가능해질 수 있습니다.
$p-1 = p_1^{e_1} \times p_2^{e_2} \times p_3^{e_3} \times \dots \times p_k^{e_k}$ 일 때 $O(e_1(logn+p_1^{0.5})+e_2(logn+p_2^{0.5})+e_3(logn+p_3^{0.5})+\dots+e_k(logn+p_k^{0.5}))$ 에 이산 로그 문제를 해결할 수 있게 됩니다.
Pohlig-Hellman Algorithm의 핵심은 $a^x = b$를 만족하는 $x$를 $p_i^{e_i}$로 나눈 나머지를 $x’$이라고 할 때 $(a^((p-1)/(p_i^{e_i}))^(x’) = b^((p-1)/(p_i^{e_i}))$이라는 것입니다. 그렇기에 각 $p_i$에 대해 $x$를 $p_i^{e_i}$로 나눈 나머지를 모두 구한 후에 Chinese Remainder Theorem을 사용하면 $x$를 복구할 수 있습니다. 그리고 $x$를 $p_i^{e_i}$로 나눈 나머지를 구하는 과정에서 Baby-step Giant-step Algorithm을 활용할 수 있습니다. 전체 코드는 아래와 같습니다.
def egcd(a1, a2):
x1, x2 = 1, 0
y1, y2 = 0, 1
while a2:
q = a1 // a2
a1, a2 = a2, a1 - q * a2
x1, x2 = x2, x1 - q * x2
y1, y2 = y2, y1 - q * y2
return (x1, y1, a1)
def inv(a, m):
x, y,g = egcd(a, m)
if g != 1:
raise Exception('No modular inverse')
return x%m
def crt(a, m):
n = len(m)
ret = a[0]
mod = m[0]
for i in range(1,n):
m1 = mod
mod *= m[i]
m2inv = inv(m[i],m1)
m1inv = inv(m1,m[i])
ret = (ret*m[i]*m2inv+a[i]*m1*m1inv)%mod
return ret
def func2(a, b, p):
table1 = []
k = int(p**0.5)
val = 1
mul = pow(a,k,p)
for i in range(0,p,k):
table1.append((val, i//k))
val = val * mul % p
table2 = []
ainv = inv(a,p)
val = b
for i in range(k):
table2.append((val, i))
val = val * ainv % p
table1.sort()
table2.sort()
idx1 = 0
idx2 = 0
while idx1 < len(table1) and idx2 < len(table2):
if table1[idx1][0] < table2[idx2][0]:
idx1 += 1
elif table1[idx1][0] > table2[idx2][0]:
idx2 += 1
else:
return k*table1[idx1][1]+table2[idx2][1]
return -1
def MITM(a, b, mod, pp):
table1 = []
k = int(pp**0.5)
val = 1
mul = pow(a,k,mod)
for i in range(0,pp,k):
table1.append((val, i//k))
val = val * mul % mod
table2 = []
ainv = inv(a,mod)
val = b
for i in range(k):
table2.append((val, i))
val = val * ainv % mod
table1.sort()
table2.sort()
idx1 = 0
idx2 = 0
while idx1 < len(table1) and idx2 < len(table2):
if table1[idx1][0] < table2[idx2][0]:
idx1 += 1
elif table1[idx1][0] > table2[idx2][0]:
idx2 += 1
else:
return k*table1[idx1][1]+table2[idx2][1]
return -1
def func4(a, b, p):
factors = []
i = 2
tmp = p-1
while tmp >= i*i:
if tmp % i != 0:
i += 1
continue
cnt = 0
while tmp % i == 0:
tmp //= i
cnt += 1
factors.append((i, cnt))
i += 1
if tmp != 1:
factors.append((tmp, 1))
crt_a = []
crt_m = []
for factor in factors:
pp, ee = factor
cura = pow(a, (p-1)//(pp**ee), p)
curb = pow(b, (p-1)//(pp**ee), p)
gamma = pow(cura, pp**(ee-1), p)
exp = 0
for i in range(ee):
b_tmp = inv(pow(cura, exp, p), p) * curb % p
b_tmp = pow(b_tmp, (pp**(ee-1-i)), p)
# Want to find gamma ** x = b_tmp (mod p), x in (0,1,2,...,pp-1)
exp += MITM(gamma, b_tmp, p, pp)*pp**i
crt_a.append(exp)
crt_m.append(pp**ee)
return crt(crt_a, crt_m)
a = 7
b = 12423425
p = 4766587461926291
x = func4(a,b,p)
print(x, pow(a,x,p)==b)
Pohlig-Hellman Algorithm을 이용하면 $4766587461926291 = 2 \times 5 \times 7 \times 11 \times 13 \times 17 \times 19 \times 23 \times 29 \times 31 \times 37 \times 41 \times 47+1$과 같은 수에 대해 이산 로그를 빠르게 구할 수 있습니다.
Safe Prime
Pohlig-Hellman Algorithm에서 볼 수 있듯 $p-1$의 소인수 중에 그다지 큰 것이 없다면 이산 로그를 굉장히 쉽게 구할 수 있습니다. 이를 막기 위해 $p$를 safe prime으로 택하는 것이 좋습니다. safe prime은 $p = 2q+1$ 꼴의 소수를 의미합니다.($q$또한 소수입니다.) 그런데 이러한 safe prime을 어떤 식으로 만들어낼 수 있을까요? 2048-bit의 safe prime을 택하기 위해서는 1024-bit의 prime $q$를 임의로 택합니다. 그리고 해당 $2q+1$이 소수인지 확인하는 방식으로 만들어낼 수 있습니다. $2q+1$이 소수일 확률은 소수 정리에 의해 $1/ln(2q+1)$에 근사하기 때문에 대략 2048개의 $q$를 잡으면 safe prime을 만들어낼 수 있습니다.
맺음말
이번 게시글에서는 이산 로그 문제에 대해 다뤄보았습니다. 이산 로그 문제는 소인수분해 문제와 더불어 현대 암호학에서 다양한 곳에 쓰이고 있습니다. 특히 Diffie-Hellman 키 교환의 경우, 우리가 일상적으로 웹에 접속할 때 이루어지는 TLS Handshake 과정에서도 쉽게 찾아볼 수 있습니다.
이 글을 읽고 더 공부를 해보고 싶다면 Diffie-Hellman 키교환, Digital Signature Algorithm, Eliptic curve에 대해 알아보시는 것을 추천드립니다.