cjmp1's profile image

cjmp1

June 17, 2019 22:51

data science 기초

data-science

Data Science 의 기초

contents

  • what is data science?
  • ready to start
  • analysis feature
  • check outliers
  • PCA
  • linear regression
  • conclusion

what is data science?

데이터 과학이란?
이번 주제에서는 데이터 과학이라는 분야를 다뤄보고자 한다.
딥러닝이 현재 큰 인기와 관심이 주목된 가운데, 데이터과학의 중요도 또한 크게 중요해지고 있다.

데이터들이 중요한 이유는 무엇일까?
AI(인공지능)는 learning 을 통해서 자신의 내부 computation을 견고하게 만들고,
그 learning은 다름이 아닌 data들의 집합을 통해서 이루어진다.

여러가지 예를 들 수 있겠지만 image classification 이라는 대표적인 주제가 있다고 가정하자.
프로그래머들은 직접 만들어낸 ai가 image classification 을 효과적으로 수행하기위해, 어느 정도의 data들을 주고 학습시켜주어야 한다.
이 학습은 label들이 붙어있는 supervised learning일수도 unsupervised learning 일수도 있다.
하지만 동일한 것은 data들을 가지고 ai가 학습을한다는 것이다.
이 과정속에서 만약 유명한 MNIST 예제처럼 손글씨를 인식하는데에 있어서 사람이 보기에도 판별하기 어려운 이미지들이 간간히 보여진다.
이런 data들은 ai 학습에 있어서 안좋은 영향을 끼치며 ai알고리즘 성능이 좋아서 이런 몇몇개의 이미지들을 무시할 수 있는 결과를
보여줄 수는 있지만 안좋은 영향임은 변함이 없다.

따라서 우리는 learning에 있어서 큰 도움이 되는 단순히 이런 outlier(이상치) 판단 문제 뿐만아니라,
dataset이 주어졌을 때, 이 dataset을 효과적으로 visualization하고 data들의 의미를 파악하는 것을 다뤄보고자 한다.

Ready to start

1. Import data

데이터를 받아오는 과정이다. 데이터를 읽고 가공하는 작업을 지원하는 tool은 정말 여러가지가 있다.
그 중 가장 대표적인 것이 python library를 이용하는 것이고 matlab 또는 c++ 언어로도 원하는 작업을 잘 처리할 수 있다.

우선 data를 받아오기 위해서는 data를 찾아야 한다.
인공지능에게 주어져야 하는 적합한 data set을 직접 만들어서 파일을 만들어 놓을 수도 있고, 웹서버에서 직접 받아올 수도 있다.

데이터에는 어떤 종류가 있는지 부터 생각해볼 필요가 있다.
수치형 integer or double data 일수도 있고, true or false 를 나타내는 boolean data 일수도 있고, image data 일수도 있고, audio data 일 수도 있고 문장 text가 data가 될수도 있다.

그렇다면 이런 data들을 담는 파일에는 어떤 종류가 있는지 확인할 필요가 있다.
가장 대표적으로 CSV라는 파일이 있다. CSV(comma separate-values) 로 CSV는 테이블형으로 데이터가 저장되어있고,
parsing 이 ‘,’ 로 되어있는 파일이다. 그렇다면 csv파일을 읽는 방법 부터 확인해보자. 예제에서 사용된 data는
boston housing prediction 이라는 유명한 주제의 data로 구글링을 통해 찾을 수 있다.

import csv
import os
os.system('cls')
line_counter = 0
with open('housing.csv') as f:
    while 1:
        data = f.readline()
        if not data : break
        if line_counter == 0:
            header = data.split(",") # feature
        else:
            field = data.split(",") # data
        line_counter += 1
f.close()

Matlab 의 경우에는 좀더 간결하게 표현된다.

tab = readtable('housing.csv');
data = [tab.RM tab.LSTAT tab.PTRATIO tab.MEDV ...];

추가적으로 python 에서는 pandas 라는 library를 통해서 더 간략하고 유용하게 csv를 읽고 가공할 수 있다.

import pandas as pd
data = pd.read_csv("train.csv")
data

2. Data plotting

데이터 import 에 성공했다면 우리는 데이터 가공을 해주어야 한다.
데이터 가공에 있어서 우리가 데이터가 의미하는 것을 알고있다면 그에 맞는 가공기법을 사용해 줄 수 있을 것이다.
하지만 데이터가 의미하고있는 것이 무엇인지 모른다면 우선 데이터의 특성을 살펴볼 필요가 있다.
물론 데이터가 의미하는 것을 알고있더라도 이 특성을 살펴보는 작업은 가공을 수월하게 해주고 큰 도움이 된다.

데이터의 양이 적고 그 내용이 간단하고 직관적이라면 우리는 그냥 데이터의 수치만 보고도 데이터를 이해할 수 있지만
대부분의 경우 그렇지 않다. 따라서 데이터의 특성을 살펴보는 방법이 필요하다.

데이터의 특성을 살펴보는 것은 data를 보기좋게 plot을 하는 것에서 시작된다.
그렇다면 data를 plot하는 방법과 그 종류에 대해서 살펴보자.

먼저 python 에서는 data 를 plot할 때 matplotlib 라는 라이브러리를 사용한다.

import matplotlib.pyplot as plt
import numpy as np

plt.title("data plot") ## plot 의 이름을 지정
## x,y는 데이터 리스트 또는 array 객체이다. 
plt.plot(data) ## 2차원 상에 알아서 x 값들을 연결해준다.
plt.plot(data['RM'],data['PTRATIO']) ## 2차원 상에 표현하고, x값에 대한 y값들을 연결해준다.
plt.scatter(data['RM'],data['PTRATIO']) ## 2차원 상에 x값에 대한 y값들을 점으로 찍어준다.
plt.hist(data['RM']) ## x에 대한 히스토그램 그래프를 보여준다.
plt.boxplot(data['RM']) ## x의 boxplot을 그린다.

boxplot은 처음 접하는경우 약간 생소할 수 있는데 박스안에 들어가는 데이터가 전체의 50%를 표현하고 가운데선은 중앙값이다.

한편 seaborn 이라는 라이브러리도 존재하는데 seaborn 은 matplotlib를 기반으로 좀 더 다양한 색상을 이용한 plot들을
추가 할 수 있는 패키지이다. 다음 코드와 함께 seaborn 을 이용한 plot들을 살펴보자.

import matplotlib.pyplot as plt
import seaborn as sns
sns.pairplot(data) ## data의 header 에 대해서 각 헤더별로 짝지어 서로의 상관관계를 scatter plot으로 보여준다.
sns.heatmap(data)

데이터를 plot 했다면 데이터의 상관관계가 눈에 뚜렷하게 보일수도 아닐 수도 있다.

자 이제 가장 기본적인 데이터를 가져오고 보기 좋게 그리는 것을 해낼 수 있게 되었다. 여기서부터는 좀 더 구체적이고 세분화 되므로 우리가 다루고 있는 housing.csv 파일을 이용해 좀더 설명해보겠다.

Analysis feature

데이터에 각 column 마다 feature 들의 이름이 적혀있는 데이터가 대부분이다. 다음 그림은 train.csv를 받아와 출력한 모습이다.
traindata 위에 보이는 ID, crim, zn, … , medv 가 바로 feature에 해당된다. 각 feature가 의미하는 것은
https://www.kaggle.com/c/boston-housing 에 data description 이 나와있다.

하지만 우리는 이 데이터 feature들이 주어지지 않았다고 가정한 후에 문제를 해결해 볼 것이다.
feature이 만약 주어지지 않았다면 이 데이터로서 알 수 있는 것들을 마구 나열해보자.

  1. 각 열마다 데이터의 자료형이 integer형 / float형으로 존재한다
  2. 2번째 열은 매우 작은 값을 띈다.
  3. 4번째 열은 0 또는 1의 값을 가진다.
  4. 각 열마다 서로 특정한 범위내에서 데이터가 분포하고 있다.

정도를 파악해낼 수 있다. 이제 다음단계로 넘어가자.

Check Outliers

데이터 분석에 있어서 Outlier는 매우 안좋은 영향을 주게 된다.
여기서 Outlier란 바로 이상치로 관측된 데이터의 범위에서 아주 많이 벗어난 데이터들을 의미한다.
가장 대표적인 예로 linear regression 을 예로 들어보자 outlier을 제외한 linear regression의 결과가 y = 2x였는데
(1, -100) 이라는 outlier가 주어졌다고 생각해보자. 그렇다면 linear regression은
y = 2x 가 데이터들의 행보를 가장 잘 설명함에도 불구하고, 기울기가 매우 감소하게 될 것이다.

따라서 outlier들을 제거하는 것은 데이터 분석에 큰 도움을 준다. 그럼 outlier들을 찾아내보자.
위에서 익힌 plot 을 사용해보겠다. boxplot으로 찾아내는 것도 좋은 방법이지만 그냥 scatter plot을 사용했다
위 feature 의 순서대로 plot 한 모습이다.
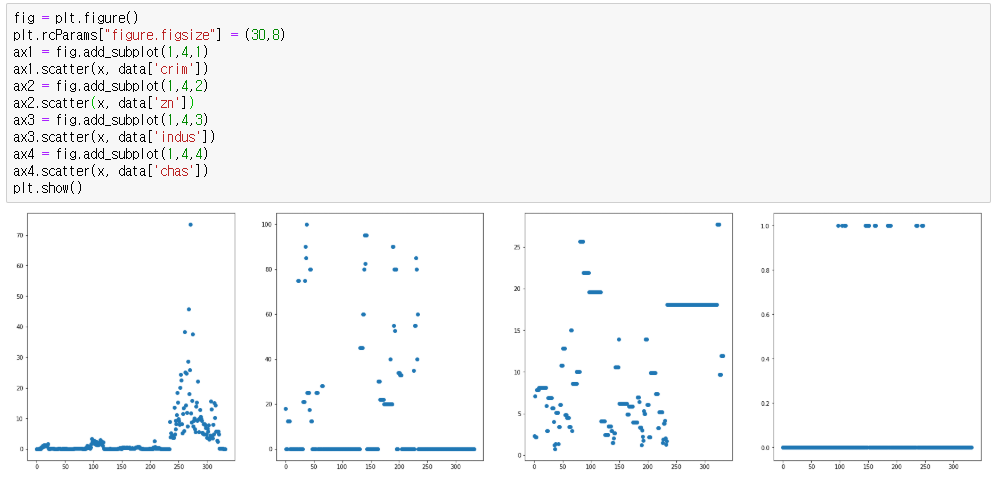outlier1 첫번째 column에서는 오른쪽 최상단에 있는 data값이 혼자 너무 큰 값을 띄고 있는 것을 확인할 수 있다.
두번재,세번재 column에서는 outlier를 쉽게 판별해낼 수 없다.
네번재 column에서는 값이 0 또는 1을 띄므로 outlier라고 할 수 없다.
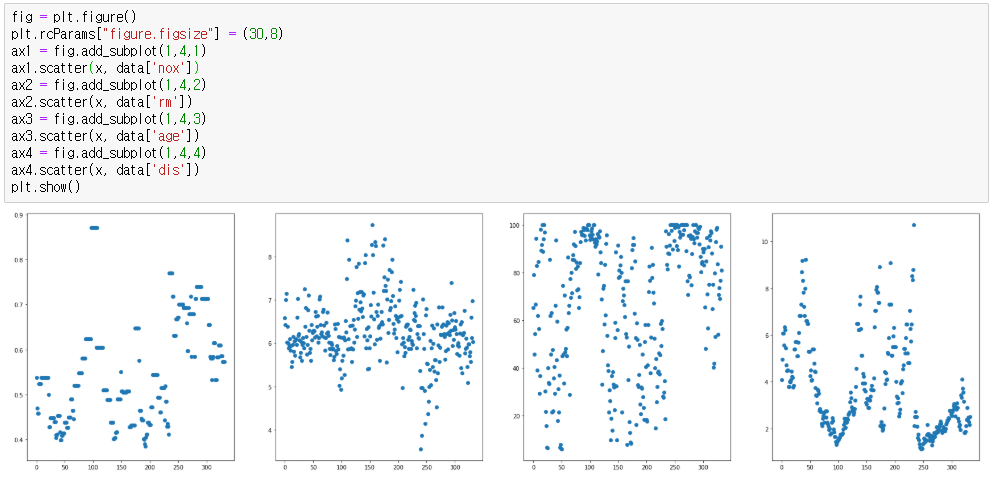outlier2 5,6,7,8번재 column은 약간의 평균에서 떨어진 값은 존재하지만 특별히 outlier라고 단정지을 수 없다.
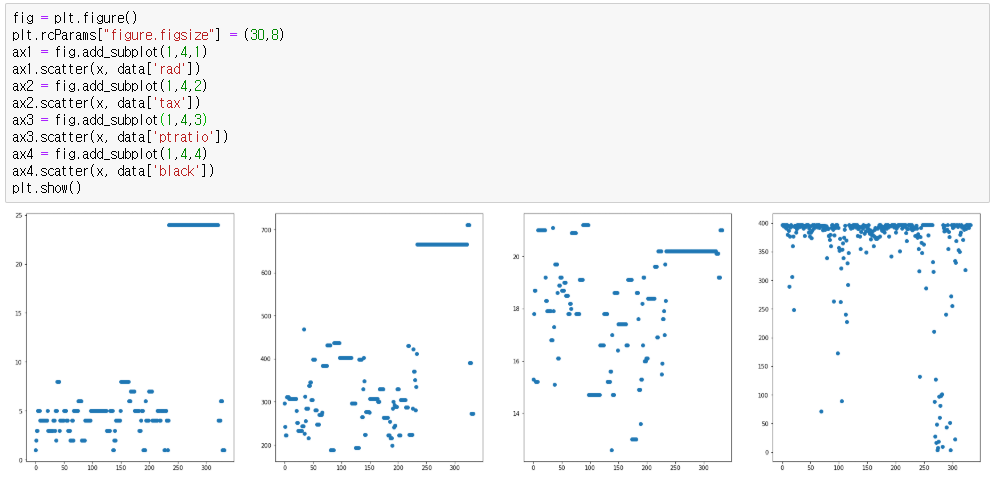outlier3 9,10,11 동일하다.
그러나 12번째 column에서는 대부분의 data가 350 이상을 웃도는데 몇몇개의 데이터가 50 이상의 작은 값을 띄는것을 확인할 수 있으므로
충분히 outlier일 가능성이 있다.

이렇게 plot들을 이용하면 outlier에 대한 그 “가능성”을 가늠해볼 수 있다. 하지만 정확한 outlier를 찾아내는 대에는 어려움이 있다.
만약 feature을 알고있는 상태라면 outlier검출이 plot만으로도 가능할 것이다. 예륻들어, 첫번째 feature는 사실 crim 즉 범죄율이었다.
보스턴주의 집가를 예측하는데에 있어서 범죄율이라는 feature가 사용되고 있는 것이다. 그런데 우리가 앞서
골라낸 우측최상단에 있는 값은 보면 범죄율이 70퍼센트를 넘어가고 있고, 30퍼센트 이상의 값들도 사실상 정상적인 수치라고 보기가 어렵다.
따라서 이런 값들이 outlier가 되는 것이다.

하지만 이는 feature가 무엇인지를 알고있을 때이고, 우리는 feature에 대해 모르는 상태에서 진행하고 있다.
그렇다면 어떻게 outlier들을 판단해 낼 수 있을까?

PCA

위의 outlier판단 기준과 더불어 여러가지를 알아 낼 수 있는 방법에 대해 소개하고자 한다.
PCA (principal component analysis) 는 주성분요소 분석이라는 이름을 가진다.
즉 주어진 데이터에서 데이터들의 주성분을 찾아내어 분석을 하는 것이다. 예를들어 데이터가 중심이 (0,0)인 원형을 이룬다고 생각해보자.
그렇다면 데이터를 가장 잘 설명하는 주성분은 x축과 y축이 된다.

좀 더 수학적으로 PCA에서 말하는 주성분요소는 데이터 분포의 분산이 가장 큰 방향벡터를 의미한다.
즉 우리는 데이터들의 집합이 있는데 이들은 feature에 대해서 수치를 나타내고 있다. 하지만 실제 모든 데이터들의 분산을
더 잘 표현해 줄 수 있는 요소를 찾고자 하는데에 목적이 있는 것이다.

그렇다면 이제 PCA를 뽑아내는 프로그램을 작성해보자. 여러가지 tool을 사용하는 법을 배우는 것 또한 목적이기 때문에
이번에는 matlab 코드를 사용했다.

clear data;
clear all;
close all;
clc;

LD = load('housing.mat');
data = LD.data;

[num_row, num_col] = size(data);
col_med_value = zeros(1,num_col);

for i = 1:num_row
    for j = 1:num_col
       if data(i,j) < 0
            data(i,j) = NaN;            
        end
        if data(i,j) >= 1000000
            data(i,j) = NaN;
        end
    end
end

for i = 1:num_col 
   col_med_value(i) = nanmean(data(:,i));
end

for i = 1:num_row
    for j = 1:num_col
        if isnan(data(i,j)) == 1
            data(i,j) = col_med_value(j);
        end
    end
end

pred = data(:, 1:end-1);
price = data(:, end);

fig = figure(1); 
w = 1 ./ var(pred);

[coeff,score,latent,tsquared,explained,mu] = pca(pred,'VariableWeights',w,'Algorithm','eig');

coefforth = inv(diag(std(pred)))*coeff; 

vbls = {'CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSAT'};
biplot(coefforth(:,1:3),'Scores',score(:,1:3),'VarLabels',vbls);

우선 .mat 라는 파일형식을 사용해서 파일을 읽어왔다. mat 은 matlab전용 확장자로 python에서도 읽어들일 수가 있다.
그 후 NAN value 나 잘못된 값이 들어있는 경우 이를 열의 중앙값으로 대체하는 작업을 진행했다.
이는 사실 현재 우리가 다루는 데이터에서는 의미가 없지만 데이터의 누락이나 손실 가능성이 있는 경우
이런 구문을 추가해주는 것이 좋다.

그 후 w = 1 ./ var(pred) 라는 구문이 있다. w 에는 각 열의 분산의 역의 값이 들어있다. 이 이유는 우리가 다루는 데이터의
각 열별로 서로 다른 범위를 지니고 있기 때문이다. 어떤 값은 0~1 사이의 값으로 되어있는 반면 300이 넘늠 값들이 대부분인 데이터가 존재한다.
이를 그냥 사용할 경우, bias가 커 제대로 된 PCA를 찾아내지 못한다.

matlab에는 pca를 계산해주는 함수가 따로 존재한다. 위에서는 pred 라는 데이터에 weights w 그리고 eigenvector 알고리즘을 사용해서
pca를 구하는 과정이다. 그 후 coefforth는 결과로 나온 coeff 를 직교좌표계로 만들었다.

자이제 pca들이 coefforth 라는 데이터에 들어가게된다. 즉 데이터들의 분산을 이용해서 새로운 요소들을 만들어 낸 것이다.
explained 라는 변수를 살펴보면 각 요소가 순서대로 몇%의 분산을 설명해주는지 나와있다. 가장 앞에있는 3개의 요소에 대한 합을 구하면
80%를 넘는 분산을 설명해주는 3가지 중요요소가 구해진다.

이 요소들이 현재 직교좌표로 만들어 주었으므로 이를 바로 plot해보자.
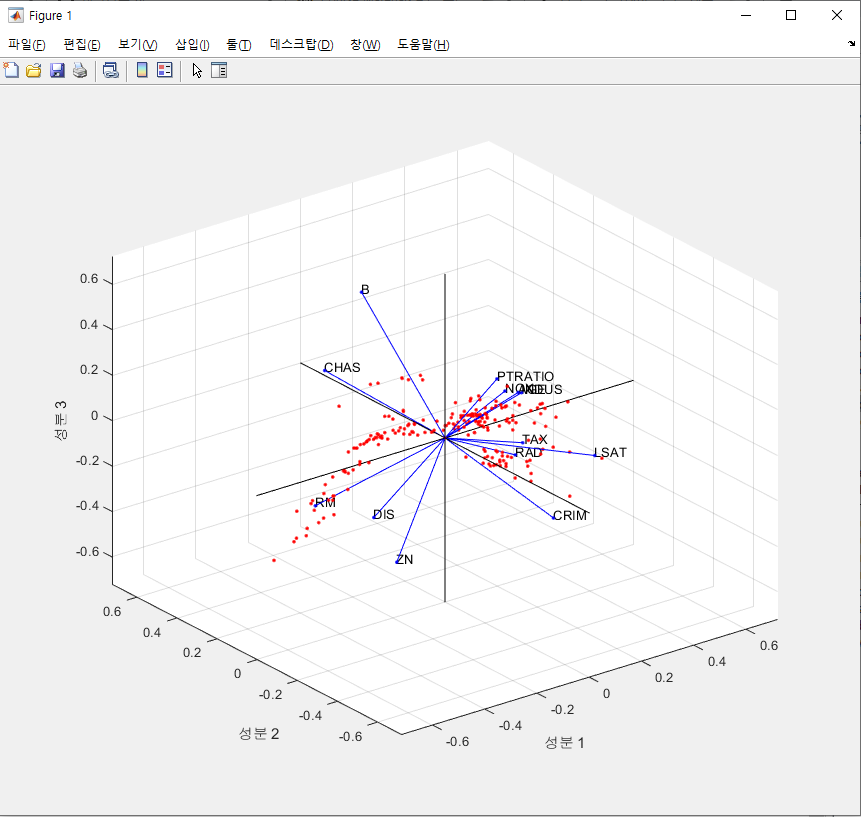biplot 이렇게 보여진 좌표계에서 우리는 보다 쉽게 outlier들을 찾아낼 수 있다.
score라는 변수에는 각 data value들의 새로운 요소에 대한 값들이 들어가 있다.
즉 기존 data 가 CRIM 이 x였다고 하면 이제는 data 의 PCA_1 이 x’ 이 되는 것이다.

주성분 요소를 이용해 데이터의 80%를 포함하는 타원구를 만들어 줄 수 있고 이에 포함되지 않는 데이터들은 outlier들로 처리해 줄 수 있다.
이렇게 outlier 처리가 끝나면 비로소 data cleaning이 종료되었고
data를 이용해 목표를 달성하기 위한 다음 과정을 진행한다.

Linear Regression

이제 outlier가 지워진 data들을 이용해서 15번재 행의 값을 도출하고자 한다.
우리는 선형회귀를 이용해서 결과를 도출해 낼 것인데 3가지 방법을 생각해 볼 수 있다.

  1. 13개의 feature를 모두 이용해서 선형회귀를 한다.
  2. 13개중 중요한 3개의 feature를 이용해서 선형회귀를 한다.
  3. PCA로 골라낸 3개의 주요소로 선형회귀를 한다.

정도가 있다.
첫번재 방법부터 진행해보자. 13개의 feature를 모두 이용하게 되므로,

P_ = [ones(206,1), pred];
a_ = P_ \ price;
fprintf("error 총합 : %f\n", norm(price-P_*a_));

으로 표현이 가능하다 여기서 \ 는 matlab에서 지원해주는 역행렬의 개념이라고 생각하면 된다. 즉 계수를 구해주는 것이다.
실제 cost_function 을 이용한 선형회귀를 하면 더 정확하지만 우리의 현재 목적은 선형회귀에 있지 않기 때문에
간단한 이 방법을 이용하겠다.
이 때 에러의 합은 63.28 정도가 나왔다.

두번재 방법으로는 13개중에서 중요한 3개의 feature를 이용하는 방법이다.
만약 우리가 feature의 정보를 알고있다면 이 3개의 feature는 쉽게 추론해볼 수 있을것이다. 예를들어 이번 데이터에서는
집값이 구하는 목표이므로
CRIM : 범죄율이 낮을수록 집값이 높을거라는 것을 쉽게 예측할 수 있고,
CHAS : 강의 boundary여부가 집값에 중대한 영향을 미칠것이다.
PTRATIO : 유명강사의 비율로 역시 학원가 라고 생각해 본다면 집값에 영항을 줄 것이라고 생각할 수 있다.

하지만 우리는 feature의 정보를 모르고 있으므로 어떤 feature가 영향을 끼치는지를 파악할 수 없다.
이를 파악하기 위해 각 feature와 15번째행의 상관관계를 살펴보고자 한다.
다시 python code로 돌아왔고 아래 코드는 feature 이름별로 했지만 이를 열 번호로 바꾸면 똑같은 방법이 된다.

fig = plt.figure()
plt.rcParams["figure.figsize"] = (30,10)
ax1 = fig.add_subplot(4,4,1)
ax1.scatter(data['crim'], data['medv'])
ax2 = fig.add_subplot(4,4,2)
ax2.scatter(data['zn'], data['medv'])
ax3 = fig.add_subplot(4,4,3)
ax3.scatter(data['indus'], data['medv'])
ax4 = fig.add_subplot(4,4,4)
ax4.scatter(data['chas'], data['medv'])
ax5 = fig.add_subplot(4,4,5)
ax5.scatter(data['nox'], data['medv'])
ax6 = fig.add_subplot(4,4,6)
ax6.scatter(data['rm'], data['medv'])
ax7 = fig.add_subplot(4,4,7)
ax7.scatter(data['age'], data['medv'])
ax8 = fig.add_subplot(4,4,8)
ax8.scatter(data['dis'], data['medv'])
ax9 = fig.add_subplot(4,4,9)
ax9.scatter(data['rad'], data['medv'])
ax10= fig.add_subplot(4,4,10)
ax10.scatter(data['tax'], data['medv'])
ax11= fig.add_subplot(4,4,11)
ax11.scatter(data['ptratio'], data['medv'])
ax12 = fig.add_subplot(4,4,12)
ax12.scatter(data['black'], data['medv'])
ax13 = fig.add_subplot(4,4,13)
ax13.scatter(data['lstat'], data['medv'])
plt.show()

이 결과는 아래 그림과 같다.
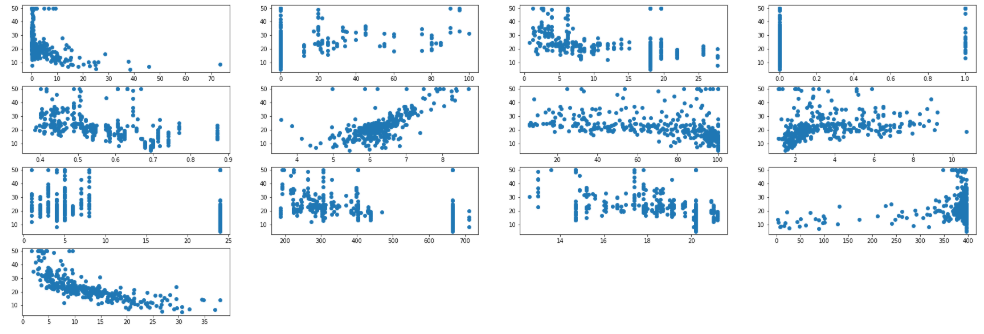
scatterAll

이 결과로 보면 rm 에서 양의 상관관계를 가진다. (x가 증가할 수록 y가 증가)
또한, lstat 에서는 반대로 상관관계를 가진다. (x가 증가할 수록 y가 감소)

이렇게 feature를 골라내는 방법도 있다.
마지막으로 모든 가능한 3가지 feature의 조합을 다 실행해보는 방법도 있다. 다음 matlab 코드이다.

comb = combnk(1:13, 3); 
r2orig = [];
for i=1:length(comb)
    P__ = [ones(206,1), pred(:,comb(i,:))];
    a__ = P__ \ price;
    r2orig = [r2orig; norm(price-P__*a__)];
end 

[min_err, min_index] = min(r2orig);
fprintf("최소 에러 : %f\n", min_err);
best_features = comb(min_index,:);

모든 가능한 조합을 계산하고 그중 최솟값을 구하고 해당 feature 를 best_features에 저장한 모습이다. 이 결과는
에러 총합이 73.40이 나왔다.

위에서 소개한 3번째 밥법을 살펴보자. PCA를 이용한 linear Regression이다.

P = [ones(206,1), score(:,1:3)];
a = P \ price;
fprintf("에러 : %f\n", norm(price-P*a));

값은 82.35로 가장 에러가 크게 나왔다.

Conclusion

우선 linear regression의 결과를 간략하게 살펴보자. PCA < BEST_FEATURE < ALL_FEATURE 순으로 성능이 좋게 나왔다.
이 이유는 무엇일까?
PCA로 선택된 최상의 요소들은 분산을 기반으로 생성됩니다. 따라서 분산이 큰 데이터 집합에 실제 데이터의 특성을 표시하는 것은 어렵다.
따라서 PCA는 실제 데이터의 의미를 기반으로 한 선형 회귀보다이 데이터 세트의 적합도가 낮다고 판별할 수 있다.

그렇다면 BEST_Feature과 ALL_feature의 차이는 왜 나는 것일까?
이 질문은 간단하다. all_feature가 더 잘 설명해주기 때문이다. 만약 feature들 중 집가격과 관련이 없는 feature가 있다면
best_feature가 더 잘 작동했을 수도 있다. 하지만 어느정도의 관련성이 모두 존재하므로 이러한 결과가 나왔다고 예상할 수 있다.

이번에는 이렇게 데이터과학의 기본을 배워보았다.
이번에 배운 기법은 데이터를 import하고 데이터를 plot해서 특성을 살피고
PCA를 이용해서 outlier를 찾아내고 실제 regression의 결과까지 살펴보는 작업을 진행했다.

하지만 데이터과학은 더 광범위한 범주를 다룬다. 다룬것들은 다 예시일 뿐이고,
big data에 따른 기법, data cleaning 의 심화된 기법, 여러가지의 analysis tool등 다양한 분야가 존재한다.

다음에는 이런 좀더 심화된 데이터과학을 다뤄보도록 할 것이고,
앞으로 이어나가 실제 인공지능망 학습 프로젝트까지 진행해보도록 하겠다.