Listen, Attend and Spell
sequence-to-sequence , attention , machine-learning , natural-language-processing
소개
전통적으로 음성 인식 모델은 음향 모델(acoustic model), 발음 모델(pronounciation model), 언어 모델(language model) 등 다양한 구성 요소로 이루어져 있었고 각각의 모델을 따로 학습하여 사용했습니다. 음성 인식 분야에서 Listen, Attend and Spell (ICASSP 2016)은 end-to-end 방식으로 학습할 수 있는 뉴럴넷 모델을 제시합니다.
Sequence to sequence with attention
Listen, Attend and Spell(LAS)는 sequence to sequence framework와 attention 기법을 사용하여 음성 인식을 합니다. sequence to sequence(seq2seq) 모델은 가변길이의 입출력 시퀀스를 학습할 수 있도록 설계되었습니다. seq2seq 모델은 encoder RNN을 통해 가변 길이의 입력 시퀀스를 받고 이를 고정 길이의 벡터로 변환합니다. 그리고 나서 decoder RNN을 통해 이 벡터를 다시 가변 길이의 출력 시퀀스로 변환합니다. 학습 시에는 decoder에 입력 값으로 실제 답을 사용하고 추론 시에는 beam search를 사용하여 각 스텝마다 출력 값 후보를 결정합니다.
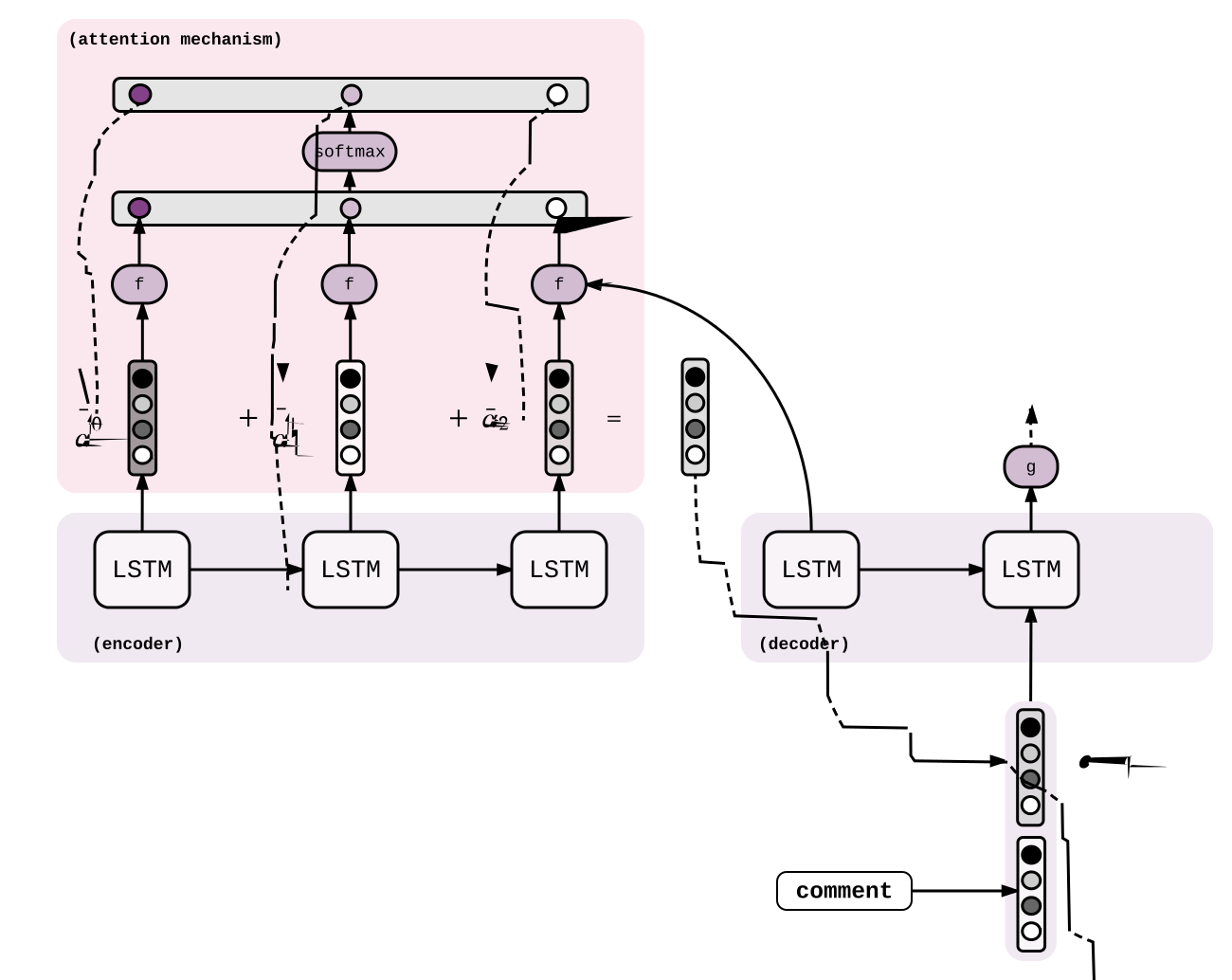
seq2seq 모델은 attention 기법을 통해 성능을 비약적으로 향상시킬 수 있습니다. decoder RNN에서 매 스탭 결과를 결정할 때마다 마지막 hidden state와 encoder의 모든 hidden state를 가지고 attention vector를 생성합니다. 이 벡터는 encoder에서 decoder로 입력 시퀀스에 대한 정보를 효율적으로 전달하는 역할을 합니다. LAS에서 attention이 어떻게 사용되었는지는 뒤에서 설명하겠습니다.
LAS model
LAS는 음향 데이터를 입력으로 받고 영어 문자를 출력으로 내보냅니다. $x=(x_1, …, x_T)$를 filter bank spectra feature로 이루어진 입력 시퀀스라고 하고 $y=(\text{
그러면 $y_i$를 다음과 같이 이전 문자들 $y_{<i}$에 대해 조건부 확률과 체인룰를 이용해서 모델링 할 수 있습니다.
| $P(y | x)=\prod_i P(y_i | x, y_{<i})$ |
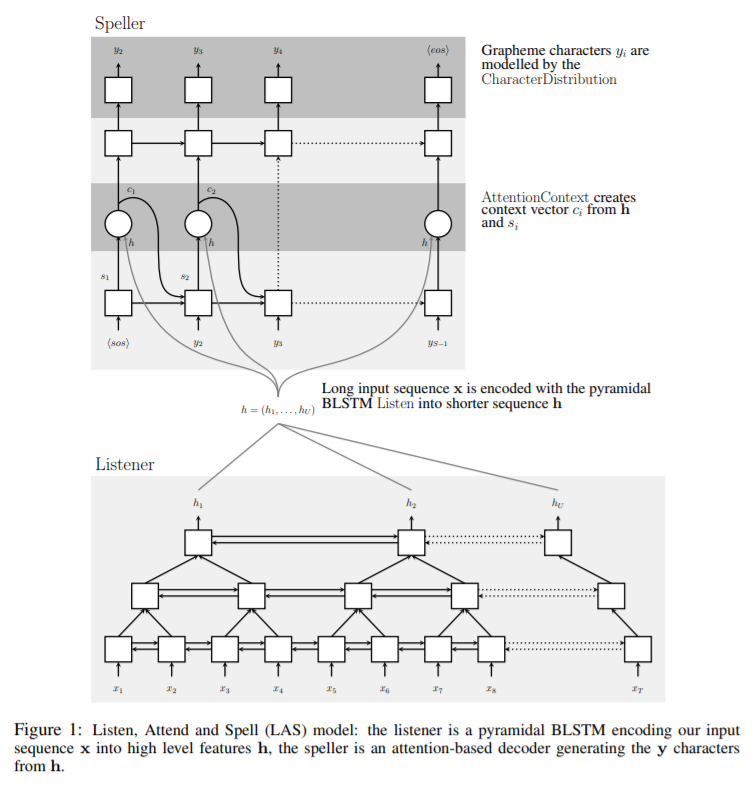
LAS는 크게 listener와 speller로 이루어져있습니다. listener는 음향 데이터를 입력받는 encoder이고 speller는 attention을 사용해서 출력을 하는 decoder입니다. 다음 수식과 같이 listener는 $x$를 high level feature인 $h=(h_1, …, h_U), U \leq T$로 변형시키는 Listen 함수로 표현하고, speller는 $h$를 가지고 출력 문자의 분포를 만드는 AttendAndSpell 함수로 표현합니다.
$h=\text{Listen}(x)$ $P(y|x)=\text{AttendAndSpell}(h, y)$
아래 그림은 LAS 모델을 시각화한 그림입니다.
Listen
Listen 연산은 Bidirectional Long Short Term Memory RNN (BLSTM)을 사용합니다. 하지만 이것을 직접 사용하면 입력 시퀀스가 매우 길때(time steps가 클 때) AttendAndSpell 연산이 오래 걸리게 됩니다. 이러한 문제를 극복하기 위해 논문에서는 pyramid BLSTM(pBLSTM)을 제안해서 매 층을 지날 때마다 시간을 절반으로 줄일 수 있도록 설계했습니다. $i$번째 time step에서 $j$번째 층의 hidden state를 $h_i^j$라고 할 때, 일반적인 BLSTM은 $h_{i-1}^j$, $h_i^{j-1}$을 가지고 $h_i^j$를 계산합니다.
$h_i^j = \text{BLSTM}(h_{i-1}^j, h_i^{j-1})$
이와는 다르게, pBLSTM 모델은 바로 직전 층에서 연속적인 두 time step의 hidden state를 연결(concatenate)하여 사용합니다.
$h_i^j=\text{pBLSTM}(h_{i-1}^j, [h_{2i}^{j-1},h_{2i+1}^{j-1}])$
논문에서는 BLSTM 층 하나에 세 개의 pBLSTM을 쌓아 listener를 구성하였습니다. 이렇게 함으로써 speller에서 기존의 입력 시퀀스보다 8배 짧은 h에 attention을 작용하게 만들어 시간복잡도를 줄였습니다.
Attend and Spell
AttendAndSpell 함수는 attention 기반의 LSTM 변환기인 decoder를 통해서 계산됩니다. decoder는 매 time step마다 이전에 결정된 문자들에 대한 다음 문자의 분포를 생성합니다. 즉, 문자 $y_i$의 분포는 decoder의 상태를 나타내는 $s_i$와 attention 정보인 $c_i$를 통해 결정된다고 할 수 있습니다. 또한, $s_i$는 $s_{i-1}, y_{i-1}, c_{i-1}$에 대한 RNN의 결과 값(hidden state)로 나타낼 수 있을 것입니다. 이를 식으로 나타내면 다음과 같습니다.
$c_i = \text{AttentionContext}(s_i, h)$ $s_i = \text{RNN}(s_{i-1}, y_{i-1}, c_{i-1})$ $P(y_i|x, y_{<i}) = \text{CharacterDistribution}(s_i, c_i)$
CharaterDistribution을 구현하기 위해서 multilayer perceptron을 사용하고 출력 값에 softmax 함수를 적용하여 각 문자가 나올 확률을 계산합니다. RNN은 두 층의 LSTM으로 구현합니다.
time step i에서 AttentionContext는 현재 decoder의 상태를 나타내는 $s_i$와 앞서 encoder에서 얻은 $h$를 가지고 컨텍스트 벡터인 $c_i$를 생성합니다. 이 값을 구하는 공식은 다음과 같습니다.
$e_{i,u}=<\phi(s_i), \psi(h_u)>$ $\alpha_{i,u} = {\exp(e_{i,u}) \over {\sum_u \exp(e_{i,u})}}$ $c_i=\sum_u \alpha_{i,u}h_u$
$\phi$, $\psi$는 MLP로 구현되며 $s_i$과 $h_u$의 내적을 구하기 위해 차원을 맞춰주는 역할을 합니다. $e_{i,u}$는 $s_i$가 $h_u$와 유사한 정도를 나타내고 이 값에 softmax 함수를 취해주면 $h_u$에 대한 가중치 $\alpha_{i,u}$를 구할 수 있습니다. 마지막으로 모든 $h_u$에 대한 가중치 합을 구하면 컨텍스트 벡터 $c_i$를 구할 수 있습니다.
Learning
앞에서 설명한 Listen과 AttendAndspell 함수는 같이 학습(end-to-end 학습)이 가능합니다. sequence to sequence 모델에서 다음 식과 같이 log 확률을 최대하는 방법으로 학습할 수 있습니다.
| $\max_{\theta} \sum_i {\log P(y_i | x, y_{<i}^\ast;\theta)}$ |
여기에서 $y_{<i}^\ast$는 모델이 실제 문자를 나타냅니다. sequence to sequence 모델에서 이와 같이 입력 값으로 이전 스텝에서 예측한 라벨이 아닌 실제 라벨을 쓰는 이유는 학습을 안정적으로 빠르게 하기 위해서 입니다.(Teacher forcing)
이 방식은 매우 효율적이지만 문자들간의 관계가 중요한 문장에서 낮은 에러를 예측하기 때문에 학습이 힘들어질 수 있습니다. 이 문제를 해결하기 위해서 일정 확률로 실제 라벨 대신에 모델에서 샘플링한 라벨을 입력 값으로 사용합니다.(Scheduled sampling)
LAS에서 수식으로는 다음과 같이 표현합니다.
$\tilde{y}i \sim \text{CharacterDistribution}(s_i, c_i)$ $\max{\theta} \sum_i {\log P(y_i|x, \tilde{y}_{<i};\theta)}$
$\tilde{y}_{i-1}$은 일정한 비율로 실제 라벨 혹은 모델로부터 샘플링한 라벨로 정해집니다.
Decoding and Rescoring
sequence to sequence 모델에서 답을 추론할 때, 다음과 같이 주어진 음향 데이터에 대해 가장 높은 확률의 문장을 선택합니다.
| $\hat{y}=\arg \max_y \log P(y | x)$ |
디코딩은 간단히 beam search를 통해 진행됩니다. 처음에는 <sos> 토큰 한 개만 있는 문장만을 partial hypothesis로 놓고, 이후 partial hypothesis에 있는 각각의 문장에 대해 문자를 하나씩 추가해보면서 최대 $\beta$개의 후보를 추려 paritial hypothesis를 관리합니다. 만약 문장에서 <eos> 토큰이 추가되었다면 해당 문장을 partial hypothesis에서 제거하고 complete hypothesis에 추가합니다. 최종적으로는 모든 남아 있는 hypothesis에서 가장 적합한 후보를 선정하게 됩니다. beam search를 할 때 추가적으로 사전을 이용해서 탐색 공간을 줄일 수 있습니다. 하지만, 실험에서는 이러한 사전이 없어도 현실의 단어를 잘 생성하는 것으로 나타났다고 합니다.
| 논문에서는 언어 모델(language model)을 사용해서 점수를 다시 매겨서 실험을 해보기도 했습니다. LAS 모델에서는 짧은 말일수록 편향이 작게 나타났다고 합니다. 이에 따라 확률을 문자 개수인 $ | y | _c$로 나누어 정규화를 했습니다. 언어 모델을 사용한 실험에서는 다음과 같은 점수를 사용했습니다. |
| $s(y | x)={\log P(y | x) \over | y | c} + \lambda \log P{LM}(y)$ |
여기에서 $\lambda$는 언어 모델의 가중치로 validation set을 가지고 결정합니다.
Experiments
실험은 300만 개의 Google voice search utterances(대략 2000시간)을 가지고 진행했습니다. 대략 10시간의 스피치를 무작위로 뽑아서 validation set으로 사용했습니다. 데이터에 노이즈와 반향도 추가해주었다고 합니다. 텍스트는 모두 소문자 영문, 숫자, 일부 특수문자(space, comma, period, apostrophe)만을 남기고 나머지는 <unk> 토큰으로 바꾸어 사용했습니다.
Listener는 세 층의 pBLSTM을 BLSTM 위에 쌓아 만들었습니다.(첫 번째 pBLSTM의 노드 수는 방향당 256개) Speller는 512개의 노드를 가진 LSTM을 두 층으로 쌓아서 만들었습니다. 그리고 가중치는 -0.1~0.1의 uniform 분포로 초기화했습니다.
모델을 학습할 때는 optimizer로 Asynchronous Stochastic Gradient Descent(ASGD)를 사용했습니다. 이 때, learning rate는 0.2로 주었고 1/20 epoch마다 geometric decay를 0.98로 주었습니다.
논문에서는 앞에서 언급했던 방법과 같이 학습시 10% 확률로 모델에서 입력 문자를 샘플링해서 사용한 경우도 실험했습니다. beam width인 $\beta$를 32로 놓았을 때 실험 결과를 정리한 표는 다음과 같습니다.
이 논문이 쓰여질 당시 state-of-the-art 모델인 CLDNN-HMM은 clean 데이터에서 WER 8.0%, noisy 데이터에서 WER 8.9%를 받았습니다. 비록 LAS는 이 모델보다 성능이 떨어지지만 end-to-end 학습이 가능한 모델이라는 점에서 의의가 있습니다.
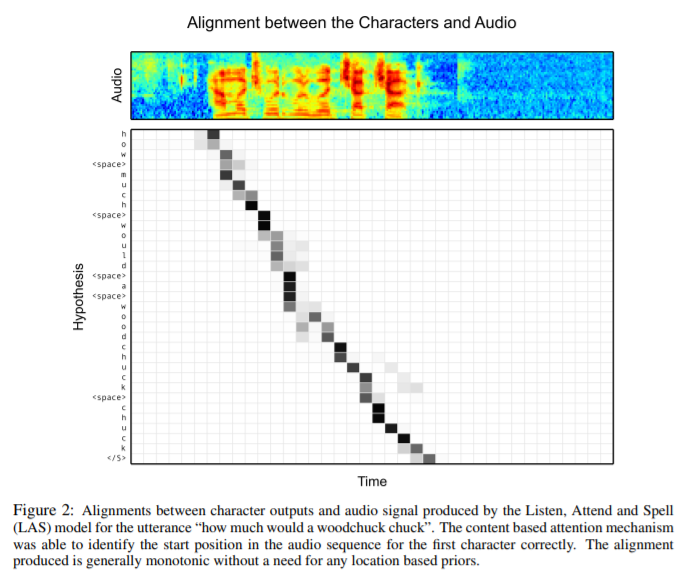
다음 사진은 “how much would a woodchuck chuck” 문장이 주어졌을 때 attention의 분포가 어떻게 나타났는지 보여줍니다. 모델에 발음에 대한 위치 정보를 주지 않았음에도 불구하고 그림과 같이 발음의 시작위치를 올바르게 찾을 수 있음을 보여줍니다. “woodchuck”와 “chuck”는 비슷한 발음을 가지고 있기 때문에 이에 대한 attention 메커니즘 결과가 약간 혼란스러운 것을 볼 수 있습니다.
흥미로운 예제
LAS에서는 같은 음향 데이터에 대해 여러 가지의 의미있는 표현을 내놓기도 했습니다. 예를 들어서 아래 표와 같이 실제 답이 “aaa”를 포함할 때 LAS의 beam search 후보군에서 “aaa”뿐만 아니라 “triple a”와 같은 단어도 확인할 수 있었습니다. 이것은 LAS가 decoder에서 다음 스텝의 문자를 예측할 때 특별히 어떠한 제약을 두지 않기 때문에 가능했을 것으로 보입니다. 기존의 CTC 모델의 경우 결과 값에 대한 독립성 가정이 존재하고, 전통적인 DNN-HMM 시스템의 경우 발음 사전을 사용하기 때문에 이와 같은 유연한 결과를 보이기 힘들 것입니다.
LAS는 content-based attention을 사용하기 때문에 디코딩을 할 때 일부 정보를 잃기 쉽다고 생각할 수 있습니다. 그래서 같은 단어를 여러 번 반복해서 출력해야 하는 예제의 경우 원래보다 적은 횟수 혹은 많은 횟수의 단어를 출력할 것이라고 예측할 수 있습니다. 하지만, 실제로 다음과 같이 한 단어를 여러번 반복 출력해야 하는 상황에서도 LAS는 성공적으로 답을 출력하는 것을 확인할 수 있습니다.
논문에서 유의할 점
LAS모델에 대해 논문 그림인 figure1이 묘사한 것과 논문의 본문에서 설명한 것이 일치하지 않는다고 생각합니다. 그 이유는 다음과 같습니다.
- 본문에서는 하나의 BLSTM에 pBLSTM을 3개 쌓아서 총 4개의 층이 있다고 설명했지만 그림에서는 3개뿐입니다.
- 그림의 Speller에서 $y_1$과 $y_S$가 존재하지 않습니다.
- Speller에서 attention은 첫 번째 LSTM 층의 결과에 적용하게 되어있습니다. 하지만, Attend and Spell 섹션에서 설명된 수식에 따르면 마지막 LSTM 층의 결과에 attention을 적용하는 것이 더 자연스러워 보입니다.
또한, 그림에 따르면 Speller의 첫 번째 LSTM 층에서 <sos> 토큰을 받는 셀은 입력 시퀀스에 대한 정보를 얻을 수 없게 설계되어 있습니다. 첫 번째 LSTM 층 각각의 셀에서 문자 벡터와 attention 벡터를 concatenate한 것을 입력한다고 이해하는 편이 자연스러워 보입니다.
참고문헌
- William Chan, Navdeep Jaitly, Quoc V. Le, Oriol Vinyals. Listen, Attend and Spell. 2015.
- Dzmitry Bahdanau, Kyunghyun Cho, Yoshua Bengio. Neural Machine Translation by Jointly Learning to Align and Translate. 2016.
- Seq2Seq with Attention and Beam Search (https://guillaumegenthial.github.io/sequence-to-sequence.html)
- What is Teacher Forcing for Recurrent Neural Networks? (https://machinelearningmastery.com/teacher-forcing-for-recurrent-neural-networks/)
- Training Sequence Models with Attention (https://awni.github.io/train-sequence-models/)