더 빠른 문제 풀이 코드를 위한 상수 줄이기

개요

알고리즘을 공부하면 언제나 등장하고, 항상 신경써야 하는 요소가 있습니다. 바로 시간 복잡도 입니다. 공간 복잡도도 중요한 요소이기는 하지만, 메모리 사용량만큼의 시간이 걸리는 알고리즘은 효율적이지 않은 경우가 많기 때문에 상대적으로 덜 언급되곤 합니다.

하지만 어느 분야나 그렇듯이 이론과 현실에는 거리가 있기 마련입니다. 정확히는 알고리즘을 공부할 때 배우는 요소들은 문제를 푸는 수학적인 방법만을 고려한 것이지만, 문제 풀이를 할 때는 그 알고리즘을 프로그래밍 언어로 구현해내야 하고, 실제로 컴퓨터를 통해 실행시켜야 하기 때문에 시간 복잡도를 계산해서 예측한 속도와는 큰 차이를 보이는 경우가 많습니다. 어떻게 보면 문제를 풀기 위해 코드를 작성하고 실행하는 과정 전체에서 알고리즘 이론에 해당하는 부분은 굉장히 작은 것일 수도 있습니다.

당장 그 프로그래밍 언어가 CPU가 인식할 수 있는 기계어로 직접 번역되는지, 가상 머신이 빠르게 실행할 수 있는 바이트 코드로 변환되는지, 또는 코드 자체를 실행할 때마다 읽는지에 따라서만도 수십, 수백 배의 속도 차이가 발생할 수 있고, 같은 언어라도 컴파일러가 얼마나 최적화를 잘 해주는지에 따라 무시할 수 없는 차이를 보이기도 합니다. 그 뿐만 아니라 실행 시점에서의 시스템 상태에 따라서도 시간 차이가 발생하는 등 예측이 불가능한 요소들도 분명히 존재합니다.

정확히 어떤 코드가 어느 정도의 시간을 걸리게 할 것인가를 판단하는 것은 컴파일러, 컴퓨터 구조, 운영체제 등의 다양한 분야에 대한 깊은 이해가 필요하기 때문에 매우 어렵습니다. 그래서 이 글에서는 코드의 실행 과정을 하나부터 열까지 파헤치기보다는, 실험을 통해 대략적인 상수를 비교하고 그에 큰 영향을 미쳤을 요소가 무엇일지 분석하여 실제 문제 풀이에서 어떤 방법을 사용하는 것이 좋을지를 알아보도록 하겠습니다.

상수(constant)란?

우선 이 글이 무엇에 대해 이야기하려는 것인지를 명확히 하기 위해, 상수가 무엇인지에 대해 먼저 설명하겠습니다.

일반적으로 어떤 알고리즘의 수행 시간이 점근적으로 $N$의 제곱에 비례한다고 할 때, 이를 점근 표기법으로 다음과 같이 표기합니다.

$O(N^2)$

하지만 이 수식 자체만으로 우리가 유추할 수 있는 건, $N$이 무한히 커져감에 따라 수행 시간이 $N^2$에 비례해서 커진다는 것 정도이지, 현실적인 범위의 $N$에 대해 모든 $O(N^3)$의 알고리즘들보다 항상 빠르다는 걸 보장하는 것은 아닙니다.

예를 들어, 다음의 세 수식은 모두 수학적으로 같은 복잡도를 나타냅니다.

$O(N^2)$ $O(2N^2+10000)$ $O(\dfrac{N^2}{10000})$

결국 이론적으로는 이 $N^2$에 $2$가 곱해지든, $\dfrac{1}{10000}$이 곱해지든, $10000$이 더해지든 시간 복잡도에 전혀 영향을 주지 못한다는 이야기가 됩니다. 다만 편의상으로 “이와 같은 알고리즘을 수행할 때는 $N^2$ 번의 연산을 두 번 수행한다” 와 같은 느낌으로 $O(2N^2)$과 같이 상수배를 붙여서 써주고는 합니다.

실제 예시를 들자면, 모든 원소의 값이 서로 다른 배열을 삽입 정렬할 때의 평균 시간 복잡도는 $O(N^2)$이지만, 실제로 원소를 비교하는 횟수를 세어보면 대략 $\dfrac{1}{4}N^2$번 정도임을 알 수 있습니다. 이는 단순하게 구현한 버블 정렬이 항상 $\dfrac{1}{2}N^2$번 정도의 비교를 요구하는 것과는 대조됩니다. 그렇지만 우리는 이것을 시간 복잡도에 반영하지 않고, 둘 다 같은 $O(N^2)$ 알고리즘이라고만 배울 뿐입니다.

그런데 이전의 특별한 정렬 알고리즘들 글에서 다루었듯이, 삽입 정렬은 실제로 $N$이 작을 때에는 매우 빠르게 동작하기 때문에 분할 정복 기법을 사용하는 정렬 알고리즘들은 대체로 범위가 작아질 경우 삽입 정렬을 사용해서 퍼포먼스를 높이곤 합니다. 이론에서 다루는 시간 복잡도를 넘어서, 실제로 빠르게 동작하는 것, 즉, 상수 가 작다는 것을 이용한 것입니다.

상수에는 이렇게 눈에 띄는 연산의 횟수 가 줄어드는 경우도 있지만, 그저 실행하는 코드 자체가 다르기 때문에 큰 차이가 발생하는 경우도 있습니다. 문제 풀이에서 알아두면 좋은 상수 줄이기 테크닉에는 어떤 것들이 있는지를 지금부터 알아보도록 하겠습니다.

실험 환경

먼저 여러 코드들의 성능을 실험하기 위한 실험 환경은 다음과 같습니다.

Intel Core i5-8250U CPU 1.60GHz
Ubuntu 18.04.1 LTS
g++ 7.4.0
- -O2

입출력

입출력은 아마도 가장 유명하면서도 많은 사람들의 골치를 아프게 한 무거운 연산일 것입니다. 백준 온라인 저지를 이용하는 사람들이라면 채점 환경에 특화된 실험 결과(입력, 출력)를 보면 좋습니다.

ios_base::sync_with_stdio(false)

이 문장은 이제는 너무나 유명해서 C++의 cin, cout으로 문제 풀이를 하는 분들이라면 거의 필수로 사용하고 있습니다. 그러나 이 문장이 왜 입출력 속도를 향상시키는지는 잘 알아보지 않으신 분이 많습니다.

C++은 C에 기반하여 만들어진 언어이고 C의 라이브러리들 또한 거의 그대로 사용할 수 있게 제공해 줍니다. 이 중에서는 표준 입출력 스트림(stdio)이 포함되는데, C++은 기본적으로 C의 입출력 스트림과 C++의 입출력 스트림(iostream)을 혼용해서 사용하더라도 문제가 없도록 iostream과 stdio를 동기화(synchronize)해두고 시작합니다. 그 때문에 iostream의 입출력 스트림을 사용할 때마다, stdio의 버퍼로부터 내용을 읽거나 stdio의 버퍼에 내용을 쓰며 동기화를 유지해주게 됩니다. 하지만 이 문장이 호출되면, 인자로 전달되는 false가 나타내듯이 둘 사이의 동기화를 해제하게 됩니다. 그러면 iostream은 자신만의 입출력 버퍼를 가질 수 있게 되어, stdio의 눈치를 보지 않고 입출력을 수행할 수 있게 되기 때문에 빨라지는 것입니다. 위의 링크에서의 실험 결과를 보면 그 차이를 실감할 수 있습니다.

다만 이를 사용할 경우 제약이 하나 생기는데, 버퍼가 분리된 후에는 더 이상 iostream과 stdio를 병행해서 사용할 수 없다는 것입니다. 동기화를 끊었으니 당연한 일입니다.

cin.tie(NULL), 그리고 endl 대신 ‘\n’

대부분의 C++ 서적에서는 cout 출력 시 개행을 하기 위해 endl을 사용하게 합니다. 사실 당연한 것이, '\n'에는 버퍼를 flush하는 기능이 없기 때문에, 출력문이 실행된 후에도 콘솔에 결과가 바로 보이지 않을 수 있기 때문입니다. 그런데 endl이나 flush 등을 사용하지 않아도 cout을 flush하게 만드는 기능이 하나 더 있습니다. 바로 cin을 사용하는 것입니다.

아마도 그런 기능이 cin에 들어있는 이유는 프로그래머가 어떤 입출력 방식을 사용하더라도, 입력을 받을 때 그 전까지 출력한 내용은 모두 보이게 하는 것이 사용자와의 상호작용에 있어 편리하기 때문일 것입니다. 그런데 이는 문제 풀이를 하는 데에 있어서는 굉장한 골칫거리입니다. 왜냐하면 flush라는 것은 입출력에 있어 가장 느리다고 해도 과언이 아닌 작업이기 때문이고, 출력할 양보다는 flush하는 횟수가 중요하기 때문입니다.

대부분의 문제에서는 입력을 모두 받은 후 출력을 하거나, 입력에 비해 출력의 횟수가 매우 적기 때문에 크게 문제되지 않지만, 매우 중요해지는 경우가 있습니다. 바로 쿼리 문제들입니다. cin.tie(NULL)은 바로 이러한 문제를 말끔하게 해줄해 주는 장치입니다.

이름 그대로 tie라는 것은 한 스트림을 다른 스트림에 묶는 역할을 합니다. 인자가 말해주듯이, 어떤 스트림을 넘겨주는 것이 아닌 NULL 포인터를 넘겨주므로 cin은 이후로 어떤 스트림에도 묶여있지 않게 됩니다. 즉, 이 이후로는 cin을 사용하더라도 cout의 flush가 발생하지 않습니다.

주의할 점은 이 이후에도 endl은 여전히 cout을 flush 시키므로 사용해서는 안 된다는 것입니다. 단, 일부 문제 풀이 플랫폼에서는 상호작용(interactive) 문제나 부분 점수 문제를 채점하기 위해 버퍼를 바로 flush 할 것을 요구하기도 하는데, 이때에만 endl을 사용해주면 됩니다.

endl의 실험 결과는 위의 링크에도 있으니, 입출력을 번갈아 할 때의 실험을 해보겠습니다. 다음과 같은 코드를 작성하고, 1억 개의 1 이상 1억 이하의 정수를 랜덤으로 뽑아놓은 입력 파일에 대해 실행한 결과입니다.

#include <bits/stdc++.h>
using namespace std;
​
int main()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
​
	int n;
	cin >> n;
​
	for (int i = 0; i < n; i++)
	{
		int x;
		cin >> x;
		cout << x << '\n';
	}
}

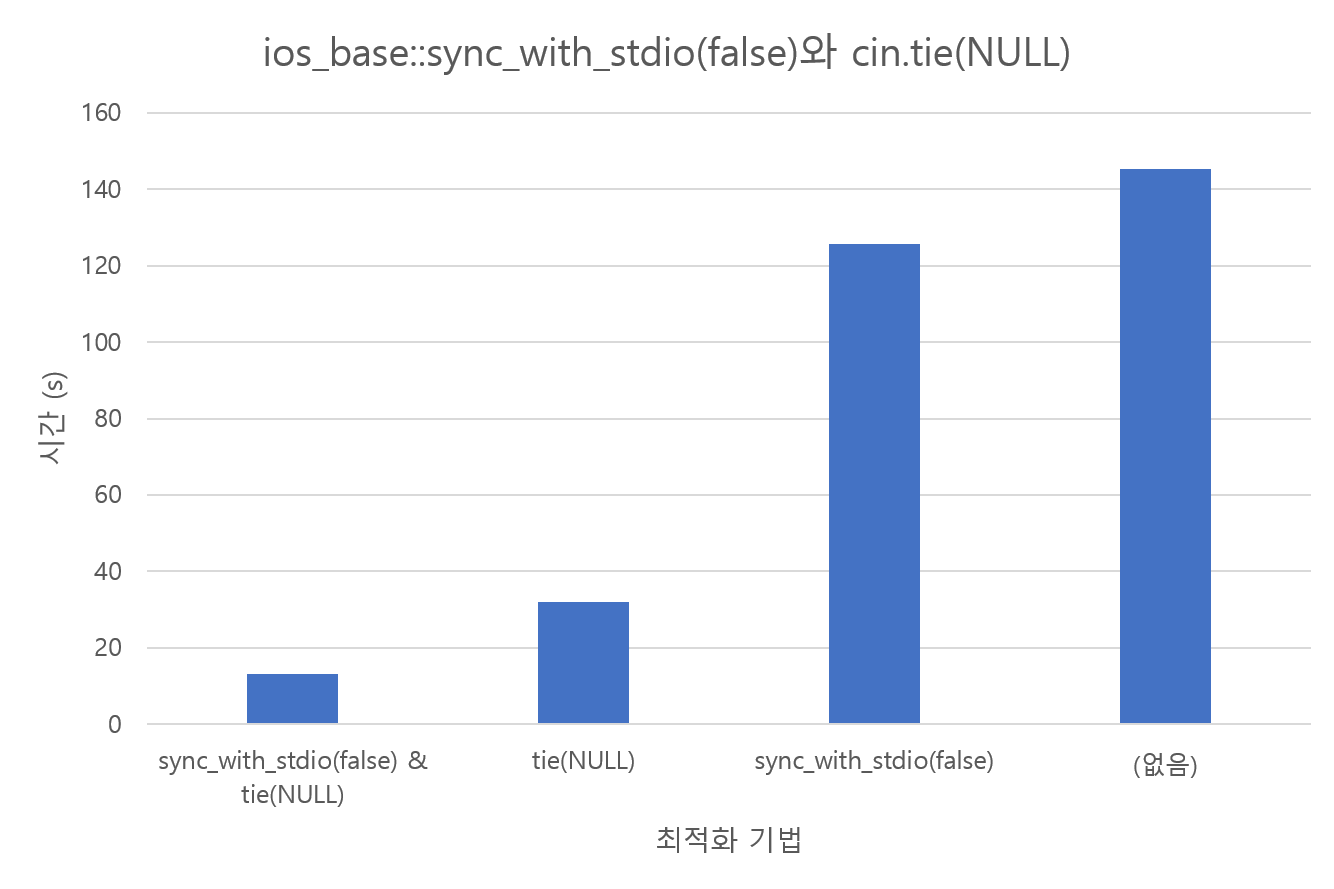
두 최적화 기법의 비교

이와 같이 flush가 발생하는 것은 cin과 cout의 버퍼를 분리하는 것과는 비교할 수 없을 정도로 큰 시간 차이를 보이는 것을 확인할 수 있습니다.

더 빠르게 - fread, fwrite

여기까지는 흔히 사용되는 최적화 방법이지만, 여전히 많은 문제에서 입출력은 병목이 되는 것이 사실입니다. 이 정도만으로도 대부분의 문제를 푸는 데에 지장이 없지만, 더욱 빠르게 입력을 받고 출력을 해서 입출력량이 많은 문제의 수행 시간을 단축해 봅시다.

fread와 fwrite는 printf, scanf보다 더 낮은 단계에서 파일 입출력을 수행하는 것이기 때문에 정수를 정수형으로 인식해주는 등의 파싱 기능을 직접 구현해야 합니다. 물론 C의 다른 라이브러리 함수들을 사용해서 파싱을 할 수도 있지만, 그런 것들을 최대한 사용하지 않고 입력 데이터를 직접 파싱해보겠습니다.

#include <bits/stdc++.h>
using namespace std;
​
const int sz = 1000000;
​
char in_buf[sz];
char out_buf[sz];
​
inline char read_next()
{
	static int i = sz;
	if (i == sz)
	{
		fread(in_buf, 1, sz, stdin);
		i = 0;
	}
	return in_buf[i++];
}
​
inline int read_int()
{
	int r = read_next() - '0';
	char ch;
	while ((ch = read_next()) >= '0' && ch <= '9')
		r = r * 10 + ch - '0';
	return r;
}
​
int w_idx;
inline void write_next(char ch)
{
	if (w_idx == sz)
	{
		fwrite(out_buf, 1, sz, stdout);
		w_idx = 0;
	}
	out_buf[w_idx++] = ch;
}
​
inline void write_int(int x)
{
	char s[10];
	int i = 0;

	do {
		s[i++] = x % 10;
		x /= 10;
	} while (x > 0);
​
	i--;
	while (i >= 0)
		write_next(s[i--] + '0');
}
​
int main()
{
	int n = read_int();
	for (int i = 0; i < n; i++)
	{
		write_int(read_int());
		write_next('\n');
	}
	fwrite(out_buf, 1, w_idx, stdout);
}

좀 더 범용성을 높이려면 음수 등을 고려하거나, 다른 형식의 입력들을 처리할 수 있게 만들어야 하지만, 현재 테스트에서 요구하는 조건에 대해서만 처리할 수 있게 간략하게 작성한 버전입니다.

읽기를 위해 read_int와 read_next라는 두 함수를 만들고, 쓰기를 위해 write_int와 write_next라는 두 함수를 만들었습니다. read_next에서는 최대 sz 개의 문자를 fread를 통해 읽어오고, 다음 읽을 문자의 인덱스를 기억했다가 버퍼의 해당 인덱스로부터 가져와 반환합니다. write_next에서는 반대로 sz개의 문자를 버퍼에 모았다면 fwrite로 쓰게 한 다음, 다음 문자를 쓸 인덱스를 기억했다가 버퍼의 해당 인덱스에 저장합니다.

read_int에서는 문자열로부터 정수값을 단순한 방법으로 만들어내는데, 가장 높은 자리를 읽고 10배를 한 뒤 다음 자리를 더하는 방식으로 진행됩니다. 마찬가지로 write_int에서는 가장 낮은 자리부터 쓰고 10으로 나누기를 반복한 뒤, 뒤에서부터 쓰기를 진행합니다.

이 코드를 위에서 테스트한 파일로 실험해본 결과, 단 3.993초의 시간이 소요되었습니다. cin과 cout을 최대한 최적화한 것보다도 훨씬 빠르게 동작하는 것을 볼 수 있습니다.

set과 priority_queue

이번에는 $log$ 시간에 문제를 해결하기 위해 자주 사용하는 자료구조 라이브러리인 std::set과 std::priority_queue를 비교해 봅시다. set은 priority_queue가 할 수 있는 거의 모든 일을 다 할 수 있고¹, 시간 복잡도 상으로도 거의 밀리지 않기 때문에² 시간 복잡도만을 고려한다면 거의 항상 set만 사용해도 됩니다. 하지만, 실제 문제들 중에는 그렇게 만만하지 않은 것들이 있습니다.

실험을 위해 다음과 같은 동작을 수행하는 프로그램을 set과 priority_queue로 각각 만들어 봅시다.

$1$부터 $N$까지의 정수가 각각 한 번씩 랜덤 순서로 등장하는 수열을 읽고, 그 순서대로 자료구조에 삽입한 뒤 가장 큰 값부터 뽑아내기

set으로 구현한 코드는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;
​
const int N = 5000000;
​
int arr[N];
​
int main()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
​
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
		cin >> arr[i];

	clock_t st = clock();
	set<int> s;
	for (int i = 0; i < n; i++)
		s.insert(arr[i]);
	for (int i = 0; i < n; i++)
		s.erase(*s.rbegin());
	clock_t ed = clock();
​
	cout << fixed;
	cout.precision(3);
	cout << "TIme: " << (ed - st) / (double)CLOCKS_PER_SEC << endl;
}

그리고 아래는 priority_queue로 구현한 코드입니다.

#include <bits/stdc++.h>
using namespace std;
​
const int N = 5000000;
​
int arr[N];
​
int main()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
​
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
		cin >> arr[i];

	clock_t st = clock();
	priority_queue<int> pq;
	for (int i = 0; i < n; i++)
		pq.push(arr[i]);
	for (int i = 0; i < n; i++)
		pq.pop();
	clock_t ed = clock();
​
	cout << fixed;
	cout.precision(3);
	cout << "TIme: " << (ed - st) / (double)CLOCKS_PER_SEC << endl;
}

$N=5000000$에 대한 실험 결과는 다음과 같습니다.

set: 6.064s
priority_queue: 0.939s

무려 6배 이상의 차이가 발생한 것을 볼 수 있습니다. 대체 각 자료구조들이 무슨 일을 하길래 이렇게나 큰 차이가 발생하는 걸까요?

set은 일반적으로 Red–black tree를 사용합니다. 레드블랙 트리는 균형 이진 탐색 트리의 일종으로, 탐색, 삽입, 삭제 등의 연산을 최악의 경우에도 $O(logN)$ 시간에 수행할 수 있도록 매 수정 연산 후 균형을 다시 잡는 이진 탐색 트리입니다.

하지만 균형을 잡는다는 행위는 그렇게 가벼운 것이 아닙니다. 원소가 추가되거나 제거되었을 때 균형이 무너진 것을 복원하기 위해 회전(rotation)이라는 기법을 사용하는데, 이로 인해 많은 노드들의 부모/자식 관계에 변화가 생길 수 있고 노드마다 추가로 기록하는 정보에도 변화가 생기기 때문입니다. 물론 이 모든 것이 많아야 $O(logN)$번만 일어나기는 하지만, 그 중에서도 상수가 매우 큰 케이스에 속한다고 볼 수 있습니다.

반면에 priority_queue는 단순하게 구현된 힙(heap)을 사용하기 때문에, 같은 $log$ 시간이라고 해도 부모/자식 노드의 값을 비교하고 교환하는 것 외의 시간 소요가 없으며, 노드 자체도 값만 들고 있으면 되기 때문에 set의 연산들에 비하면 훨씬 가벼운 log 시간 연산이라고 할 수 있습니다.

결론적으로, 삽입된 원소 중 최대 혹은 최소만 알면 되는 경우에는 set보다는 priority_queue를 사용하는 것이 현명하다고 할 수 있겠습니다. 알고리즘 문제들 중에는 간혹 정해와 통과하기 원치 않는 풀이와의 시간 복잡도 차이가 크지 않아 시간 제한을 강하게 설정하는 경우가 있으므로, 같은 작업을 같은 시간 복잡도로 수행하더라도 더 빠르게 동작하게 만드는 법을 익혀놓는 것이 좋을 것 같습니다.

대안으로 unordered_set을 사용하여 해시의 장점인 평균 $O(1)$과 단점인 최악 $O(N)$에 걸어보는 것도 있는데, 해시는 출제자나 다른 사람에 의해 저격이 될 수 있으므로 어느 쪽이 좋을지는 상황에 맞게 판단해야 합니다.

memset, memmove, memcpy

이번에는 CPU가 제공하는 기능들을 적극 활용하는 최적화를 수행해 봅시다. 대표적인 것이 memset, memmove, memcpy인데, 정확히는 이들 자체가 CPU 명령은 아니지만 효율적인 CPU 명령들을 호출하여 빠르게 연산을 수행할 수 있도록 만들어져 있습니다.

memset, memmove, memcpy 등이 직접 구현한 것보다 훨씬 빠른 이유는 대체로 이 함수들이 CPU에서 한 번에 더 많은 수의 바이트를 옮기도록 하는 명령어를 실행하기 때문입니다. 더 구체적으로 분석하려면 어셈블리 수준에서의 분석과 CPU의 구조를 알아야 하기 때문에, 이 문단에서는 실험을 통해 이들을 사용하는 것이 직접 같은 로직을 수행하는 코드를 작성하는 것에 비해 어느 정도의 향상이 있는지만을 확인해 보겠습니다.

memset

memset은 원하는 범위의 메모리를 1바이트 단위로 설정해주는 함수입니다. 1바이트 단위이기 때문에 당연히 이보다 큰 값 단위로는 설정하지 못합니다. 간단히, 원하는 크기의 메모리를 특정 값으로 특정 횟수만큼 반복하여 설정하는 코드를 만들어 비교해보겠습니다.

#include <bits/stdc++.h>
using namespace std;
​
char arr[1000000];
​
void mymemset(void *dest, int ch, size_t count)
{
	for (size_t i = 0; i < count; i++)
		((unsigned char *)dest)[i] = (unsigned char)ch;
}
​
int main()
{
	int n, m, x;
	cin >> n >> m >> x;
​
	clock_t st, ed;
	cout << fixed;
	cout.precision(3);
​
	st = clock();
	for (int i = 0; i < m; i++)
		memset(arr, x, n);
	ed = clock();
	cout << "memset: " << (ed - st) / (double)CLOCKS_PER_SEC << "s" << endl;
​
	st = clock();
	for (int i = 0; i < m; i++)
		mymemset(arr, x, n);
	ed = clock();
	cout << "mymemset: " << (ed - st) / (double)CLOCKS_PER_SEC << "s" << endl;
}

n, m을 몇 가지로 조정하여 실험한 결과는 다음과 같습니다.

n=100000, m=100000
- memset: 0.197s
- mymemset: 3.227s
n=500000, m=500000
- memset: 5.155s
- mymemset: 82.084s
n=1000000, m=10000
- memset: 0.223s
- mymemset: 3.280s
n=10000, m=1000000
- memset: 0.106s
- mymemset: 2.963s

분명히 memset의 내부 로직은 mymemset에서 구현된 것과 비슷할 텐데도, 대충 계산해도 10배가 훌쩍 넘는 퍼포먼스 차이를 보여줌을 알 수 있습니다.

이는 실제로 문제 풀이에서도 유용하게 쓰일 수 있는데, memset의 속도는 $N \le 100000$ 정도의 $N$에 대해서는 $N$번 memset을 호출해도 1초 내에 실행될 수 있어 시간 복잡도가 $O(N^2)$임에도 불구하고 많은 문제들의 시간 제한을 통과할 수 있게 됩니다. 예를 들어, 다중 테스트 케이스 문제에서 그래프가 주어지는데 모든 케이스의 정점의 수의 합이 10만 이하라고 한다면, 본래는 초기화를 할 때 매 케이스의 정점의 수만큼만 초기화를 해야 하지만 단순히 배열 전체를 memset으로 초기화하더라도 테스트 케이스의 수가 10만 개인 경우를 통과할 수 있습니다.

물론 반드시 이렇게라도 해야만 하는 경우는 거의 없겠지만, 문제를 풀 수 있는 시간이 제한적인 상황에서 빠르게 개별적으로 초기화하는 코드를 짤 자신이 없다면 대략적인 시간을 계산한 뒤 한 줄로 초기화를 끝내는 데에 활용할 수 있을 것입니다.

memmove와 memcpy

memmove는 memcpy와 비슷한 동작을 수행하기 때문에 묶어서 설명하겠습니다.³ memset과 마찬가지로 개별 원소를 하나씩 복사하는 것에 비해 월등히 빠른 속도를 보이기 때문에 흔히 사용하는 라이브러리에서도 memcpy를 사용하는 경우를 종종 볼 수 있습니다.

역시 간단한 실험을 통해 성능을 비교해 봅시다.

#include <bits/stdc++.h>
using namespace std;
​
char arr[1000000], arr2[1000000];
​
void mymemcpy(void *dest, void *src, size_t count)
{
	for (size_t i = 0; i < count; i++)
		((unsigned char *)dest)[i] = ((unsigned char *)src)[i];
}
​
int main()
{
	int n, m, x;
	cin >> n >> m;
​
	clock_t st, ed;
	cout << fixed;
	cout.precision(3);
​
	st = clock();
	for (int i = 0; i < m; i++)
		memcpy(arr, arr2, n);
	ed = clock();
	cout << "memcpy: " << (ed - st) / (double)CLOCKS_PER_SEC << "s" << endl;
​
	st = clock();
	for (int i = 0; i < m; i++)
		mymemcpy(arr, arr2, n);
	ed = clock();
	cout << "mymemcpy: " << (ed - st) / (double)CLOCKS_PER_SEC << "s" << endl;
}

실험 결과는 다음과 같습니다.

n=100000, m=100000
- memcpy: 0.194s
- mymemcpy: 3.529s
n=500000, m=500000
- memcpy: 5.210s
- mymemcpy: 93.150s
n=1000000, m=10000
- memcpy: 0.227s
- mymemcpy: 3.689s
n=10000, m=1000000
- memcpy: 0.116s
- mymemcpy: 3.709s

memset과 거의 비슷한 경향을 보이고, 역시 직접 구현한 것과는 큰 차이가 나는 것을 볼 수 있습니다.

결론

알고리즘을 이론적으로 공부할 때에는 거의 신경쓸 일이 없지만, 결국 그 알고리즘을 실제로 구현하고 테스트해보기 위해서는 컴퓨터에서 실행을 시켜야 합니다. 컴퓨터의 구조는 굉장히 복잡하고, 상식만으로는 예측할 수 없는 행동을 많이 하기 때문에 같은 시간 복잡도를 가지는 비슷한 로직을 수행하더라도 구현된 방법에 따라 큰 성능 차이를 보일 수 있음을 이 글에서 살펴보았습니다.

또한 다양한 알고리즘 대회나 코딩 테스트 등에서 코드를 평가할 때도 사람이 읽고 판단하는 것이 아닌, 단순히 그 프로그램을 돌려서 걸리는 시간을 측정하는 방식으로 이루어지기 때문에 실제로 어떤 코드가 더 빨리 수행될 것인가를 파악하는 능력은 매우 중요하다고 할 수 있겠습니다.

중복이 있을 수 있다면 std::multiset을 사용하면 됩니다. ↩
개별 연산의 종류에 따라서는 $O(logN)$과 $O(1)$ 정도의 차이가 있을 수는 있으나, 원소를 모두 삽입하고 제거하는 총 과정은 결국 똑같이 $O(NlogN)$이 됩니다. ↩
memmove는 옮기는 영역이 겹치는 경우 마치 임시 메모리 공간에 내용을 복사한 뒤 다시 옮기는 것처럼 동작하나, 실제로는 원본 위치와 목적지 주소의 대소 관계에 따라 앞에서부터 또는 뒤에서부터 옮기는 방법을 통해 겹치는 문제를 해결하도록 구현한다고 합니다. 반면 memcpy는 겹치는 영역이 있는 경우 undefined behavior입니다. ↩