Randomize algorithm
안녕하세요? 저번 글에서는 karger’s algorithm에 대한 글을 써보았습니다.
이번 글에서는 그에 이어 또다른 randomize algorithm인 Freivald’s algorithm과 기타 다른 randomize된 기법들에 대해 간단히 설명해보겠습니다.
Freivald’s algorithm
행렬 A, B, C가 주어졌을때 A*B=C를 만족하는지 어떻게 확인할 수 있을까요? 물론 직접 곱해본다면 간단하게 확인할 수 있지만, 행렬의 곱은 시간이 굉장히 많이 소요되는 작업입니다. 무려 $O(n^3)$ 만큼의 시간이 소요됩니다.
물론 이 시간복잡도를 더 줄이는 방법이 존재하긴 합니다. 슈트라센 알고리즘을 사용하면 복잡도를 $O(n^{2.807})$로 줄일 수 있고, 분할을 더 잘 하면 복잡도를 더 줄일 수 있습니다. 현재 최고 기록은 Coppersmith-Winograd algorithm으로, 약 $O(n^{2.373})$의 시간 복잡도를 가집니다만 구현하기도 어렵고 상수도 매우 큽니다.
하지만, 랜덤화된 알고리즘을 사용하면 $O(n^2)$의 복잡도에 이를 확인할 수 있는 방법이 존재합니다. 바로 Freivald’s algorithm입니다.
알고리즘은 굉장히 간단합니다. 편의상 행렬 A, B, C의 크기가 $n \times n$이라고 가정해봅시다. (꼭 정사각형 행렬일 필요는 없습니다)
그리고 0과 1로 랜덤하게 구성된, 임의의 $n \times 1$ 크기의 행렬 $R$을 만듭니다. $A \times B \times R$과 $C \times R$을 구한 뒤, 결과가 같으면 true, 결과가 다르면 false를 반환합니다. 이 방법은 A * B=C일 때는 항상 맞는 결과를 반환하고, A * B ≠ C일 때에는 이를 k번 반복할 경우 $1 - 2^{-k}$의 확률로 정확한 결과를 얻어낼 수 있습니다.
어떻게 이런 결과가 가능할까요?
먼저 $A \times B = C$일 경우, $A \times B \times R = C \times R$ 또한 성립하는 것은 자명합니다. 따라서 항상 true를 반환하게 됩니다. 그렇다면 $A \times B \neq C$일 때 false가 반환될 확률은 얼마일까요?
$A \times B \neq C$일 때, $D = A \times B - C$라 하면 D에는 0이 아닌 원소 하나 이상이 포함되게 됩니다. 이 원소가 i행, j열에 있다고 가정하고, $d_{ij}$라 합시다.
D의 i행과 우리가 랜덤하게 만든 행렬 R을 곱하면 $p_i$라 하면, $p_i$는 다음과 같은 값이 됩니다.
$p_i = d_{i1}r_{1} + d_{i2}r_{2} + … + d_{ij}r_{j} + … + d_{in}r_{n}$
이 때 편의상 $y = p_i - d_{ij}r_{j}$라 정의합시다.
true가 반환되려면, $p_i$값이 0이어야 합니다.
베이즈 정리에 의해, 이 확률은 다음과 같이 표현할 수 있습니다.
$P[p_i = 0] = P[p_i = 0 | y = 0] \cdot P[y = 0] + P[p_i = 0 | y \neq 0] \cdot P[y \neq 0]$
$p_i = 0$일 때 $y = 0$이려면 $r_j$는 0이여야 하며, 따라서 $P[p_i = 0 | y = 0] = \frac{1}{2}$입니다. 또, $p_i = 0$일 때 $y \neq 0$이려면 $r_j$는 무조건 1이여야 합니다. 따라서 $P[p_i = 0 | y\neq 0] <= \frac{1}{2}$입니다.
이제 위 식에 대입하면, $P[p_i = 0] \le \frac{1}{2} \cdot P[y = 0] + \frac{1}{2} \cdot P[y \neq 0] = \frac{1}{2}$이 됩니다. 즉, true를 반환할 확률이 $\frac{1}{2}$ 이하가 됩니다. 바꾸어 말하면, 옳은 결과(false)를 반환할 확률이 $\frac{1}{2}$ 이상입니다. 이를 k번 반복하면, 당연히 옳은 결과를 반환할 확률이 $\frac{1}{2^k}$가 됩니다.
Find Approximate Median
길이 n의 수열이 있을 때, 이 수열의 median을 찾는 것은 그리 쉽지 않습니다.
가장 쉽게 생각할 수 있는 방법은 배열을 sorting한 뒤 중간 인덱스의 값을 return하는 것으로, $O(n \log{n})$의 시간이 소요됩니다.
조금 더 효율적인 방법으로는 median of medians 알고리즘으로, 최악의 경우에도 $O(n)$의 복잡도를 보장하는 알고리즘이 존재합니다.
하지만, 정확한 median을 찾지 않고, 대략적인 median을 찾는 경우로 문제를 약간 바꾸어보면 어떨까요?
예를 들어, 배열의 25%~75%사이 범위 안에 들어있는 값을 찾는 문제는 조금 더 효율적으로 풀어낼 수 있을까요?
단순히 k개의 원소를 뽑고, 그 중 중앙값을 썼을 경우를 생각해봅시다. 먼저 이러한 연산을 하는 데에는 $O(k \log{k})$만큼의 시간이 소요됩니다.
이 때의 k개의 원소의 중앙값이 배열의 25%~75%사이 범위 안에 들어있을 확률은 얼마나 될까요?
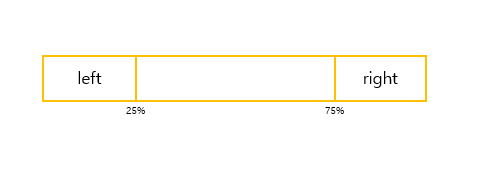
중앙값이 해당 범위 밖에 존재하려면, 다음 그림의 left 또는 right에 k/2개 이상의 원소가 들어가있어야 합니다.
k/2개 이상의 원소가 left에 속할 확률은 다음과 같이 계산할 수 있습니다.
$P = \sum_{i = k /2}^{k} \binom{k}{i} \frac{1}{4^i} (\frac{3}{4})^{k-i}$
$\le \binom{k}{k/2} \sum_{i = k /2}^{k} \frac{1}{4^i} (\frac{3}{4})^{k-i}$
$= \binom{k}{k/2} (\frac{3}{4})^k\sum_{i = k /2}^{k} (\frac{1}{3})^i$
$\le \binom{k}{k/2} (\frac{3}{4})^k \frac{3}{2} (\frac{1}{3})^{\frac{k}{2}}$
$\le \frac{1}{2} 4^{\frac{k}{2}} (\frac{3}{4})^k \frac{3}{2} (\frac{1}{3})^{\frac{k}{2}}$
$\le 4^{\frac{k}{2}} (\frac{9}{16})^{\frac{k}{2}} (\frac{1}{3})^{\frac{k}{2}}$
$= (\frac{3}{4})^{\frac{k}{2}}$
$= (\frac{\sqrt{3}}{2})^{k}$
따라서 $k = 2 \log_{\frac{3}{\sqrt{3}}}{n}$로 잡으면, $P \le \frac{1}{n^2}$이 됩니다.
right에 속할 확률도 마찬가지이고, 두 확률이 disjoint 하므로 기대할 수 있는 확률은 $P \le \frac{2}{n^2}$입니다.
또한 총 소요시간은 $O(k \log{k}) = O(\log {n} \log{\log{n}})$이 됨을 확인할 수 있습니다.
이러한 Approximate Median을 찾는 방법은 quick sort에서 pivot을 찾을 때 등에 적용될 수 있습니다.
그 외
확률에 의존하는 randomize 알고리즘에는 다음과 같은 것들이 있습니다. 이 글에서 자세히 다루지는 않고, 간단하게만 소개하고 넘어가겠습니다.
Treap
treap은 balanced binary search tree의 일종입니다. 각 노드마다 랜덤한 하나의 값이 배정되며, 이 배정된 랜덤한 값이 max heap을 만족하도록 binary search를 구성합니다.
물론 최악의 경우 높이가 $O(n)$이 될 수 있지만, 이러할 확률은 지극히 낮고 높이의 기댓값은 $O(\log{n})$이 됩니다.
더 자세한 내용은 이곳을 참고하실 수 있습니다.
밀러-라빈 소수판정법
여러 소수판정법 또한 랜덤 확률에 의존하는 경우가 많습니다. 유명한 판정법인 밀러-라빈 소수판정법(Miller-Rabin primality test)은 라그랑주 정리를 이용하는데, 임의의 수 x에 대해 k번의 테스트를 진행할 때 잘못된 판정을 내릴 확률은 $4^{-k}$입니다.
더 자세한 내용은 이곳을 참고하실 수 있습니다.
마무리
일반적인 알고리즘 문제의 경우 항상 정확한 답을 낼 것을 요구하기 때문에 랜덤화된 알고리즘을 쉽게 적용하기는 어렵지만, 현실에서는 완벽한 답을 구하는 것보다 적당히 좋은 답을, 더 빠른 시간 내에 구하는 것이 더 중요할 때도 있습니다. 많은 랜덤화 알고리즘은 그러한 상황에서 좋은 무기가 될 수 있을 거라 생각하며 이번 글을 마치겠습니다. 감사합니다.