서론
2019년 2019년 11월 9일 토요일에 ACM-ICPC 서울 리저널이 진행 되었다. 대회에 대한 정보는 http://icpckorea.org 에서 찾아볼 수 있다. (학교 기준으로) 1등은 모든 문제를 해결한 서울대학교의 Cafe Mountain, 2등은 9문제를 패널티 1004분으로 해결한 연세대학교의 Inseop is Korea top, 3등은 9문제를 패널티 1464분으로 해결한 KAIST의 CMD이다.
올해에는 12문제가 출제 되었고, 이 문제들에 대한 풀이를 작성해보려고 한다.
A - Fire on Field
문제
$A[0] = 1, A[1] = 1$ 이고, 2 이상의 $i$에 대해, $A[i]$ 를 모든 가능한 $k > 0, i - 2k \ge 0$ 을 만족하는 $k$에 대해서, $A[i], A[i-k], A[i-2k]$가 등차수열이 되지 않도록 하는 (즉, $A[i]-A[i-k] \neq A[i-k] - A[i-2k]$) 최소한의 값이라고 하자.
이 때 주어진 $n$에 대해서 $A[n]$을 구하여라. ($0 \le n \le 1000$)
풀이
문제에서 주어진 대로 구현을 하는 것이 기본 아이디어이다. 위의 항을 이항 하면, $A[i] \neq 2A[i-k] - A[i-2k]$ 가 된다. 각각 $i$에 대해서, 불가능한 $A[i]$에 값을 모두 구해 놓고, 1부터 올려가면서 가능한 값이 있는지 확인하면 된다. 이는 배열 접근 혹은 std::set 등을 이용하면 매우 쉽게 할 수 있다. 시간복잡도는 $O(n^2)$ 혹은 $O(n^2 \log n)$ 정도이다.
B - Gene Tree
문제
모든 정점의 차수가 3 이하인 트리 $T$가 하나 주어진다. 이 트리의 두 개의 리프(차수가 1인 정점)의 순서 없는 쌍들에 대해, 거리 제곱의 합을 구하여라.
좀 더 엄밀하게는, 트리 위의 두 정점 $u$와 $v$ 사이의 거리를 $d(u, v)$ 라고 하고 리프의 집합을 $L$ 이라고 할 때, $\sum_{{u, v} \subset L} (d(u, v))^2$ 을 구하여라.
($4 \le \vert T \vert \le 100,000$)
풀이
매우 잘 알려진 풀이가 여럿 있고, Centroid Decomposition을 사용하는 방법과, 트리 위에서 동적 계획법을 하는 크게 두 가지의 풀이가 있다. 이 게시글에서는 앞의 풀이를 설명하겠다.
트리의 리프가 아닌 아닌 정점 $v$에 대해, 두 리프를 잇는 경로가 $v$를 지나는 경우를 생각 해 보자. 이를 위해서 $v$를 루트로 하는 트리들과, 이 트리에서 $v$와 인접한 정점들을 루트로 하는 서브트리를 생각 해 보자. 어떤 두 리프를 잇는 경로가 $v$를 지난다는 말은, 서로 다른 서브트리에서 왔다는 뜻이다. 정점의 차수가 3 이하이므로, 모든 서로 다른 두 서브트리 사이에서 정점 $v$를 지나는 경우를 모두 고려해 주어도 3번 이하만 고려해 주면 된다.
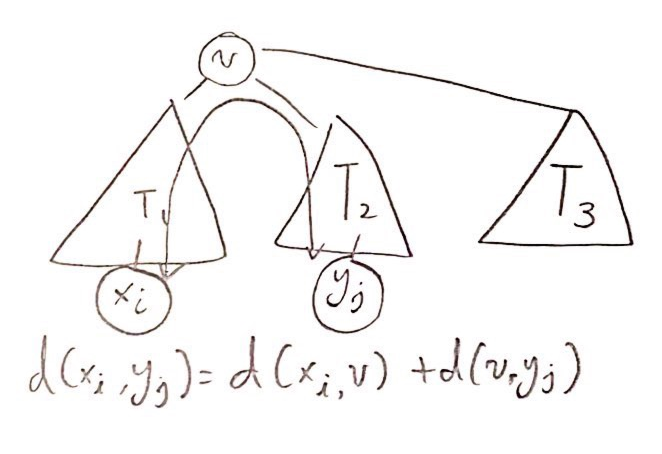
서브트리 $T_1$의 리프 $x_i$와 $T_2$의 리프 $y_j$사이의 거리는, $d(x_i, y_j) = d(x_i, v_j) + d(v_i, y_j)$ 이고, 이를 제곱 하면, $d(x_i, y_j)^2 = (d(x_i, v)+d(v,y_j))^2 = d(x_i,v)^2+2d(x_i,v)d(v, y_j)+d(v,y_j)^2$ 이다.
$T_1$의 리프 갯수가 $p$, $T_2$의 리프 갯수는 $q$ 개라고 하면, 서브트리 $T_1$과 $T_2$ 사이에서의 거리의 제곱의 합을 써보면
$\sum_{i=1}^{p} \sum_{j=1}^{q} d(x_i,v)^2+2d(x_i,v)d(v, y_j)+d(v,y_j)^2$
= $\sum_{i=1}^{p} (q d(x_i,v)^2 + 2d(x_i,v) \sum_{j=1}^{q} d(v, y_j)+\sum_{j=1}^{q} d(v,y_j)^2)$ ($j$와 무관한 항은 밖으로 꺼낼 수 있다.)
= $p\sum_{j=1}^{q} d(v,y_j)^2 + q \sum_{i=1}^{p} d(x_i,v)^2 + 2\sum_{i=1}^{p} d(x_i,v) \sum_{j=1}^{q} d(v, y_j)$ (마찬가지로, $i$와 무관한 항을 정리해준다.)
이 된다. 즉 우리는, 리프의 갯수와, 리프들의 거리의 합과, 리프들의 거리의 제곱의 합을 구해서 위의 수식을 통해 계산해 주면 된다. 이는 dfs를 통해 간단하게 $O( \vert T \vert )$ 시간에 진행할 수 있다.
이제, 우리는 정점 $v$를 지나는 경우를 고려해 주었으니까, 정점 $v$를 지나지 않는 경우를 고려해 주어야 하고, 이는 서브트리 내에서의 문제일 것이다. 즉, 우리는 이 문제에 대해서 분할정복을 사용 할 것이다. 걸리는 시간을 $X$라고 하면, $X(T) = X(T_1) +X(T_2) + X(T_3) + O( \vert T \vert )$ 이고, $ \vert T_1 \vert + \vert T_2 \vert + \vert T_3 \vert = \vert T \vert -1$ 이다. 여기서 각 트리의 크기가 $ \vert T \vert /2$ 보다 작거나 같다면, 우리는 이러한 $v$를 centroid라고 할 것이고, 이 때의 시간 복잡도는 $X(T) = O( \vert T \vert \log \vert T \vert )$ 이 나올 것이다. 우리는 이러한 centroid는 무조건 존재함을 증명할 수 있다.
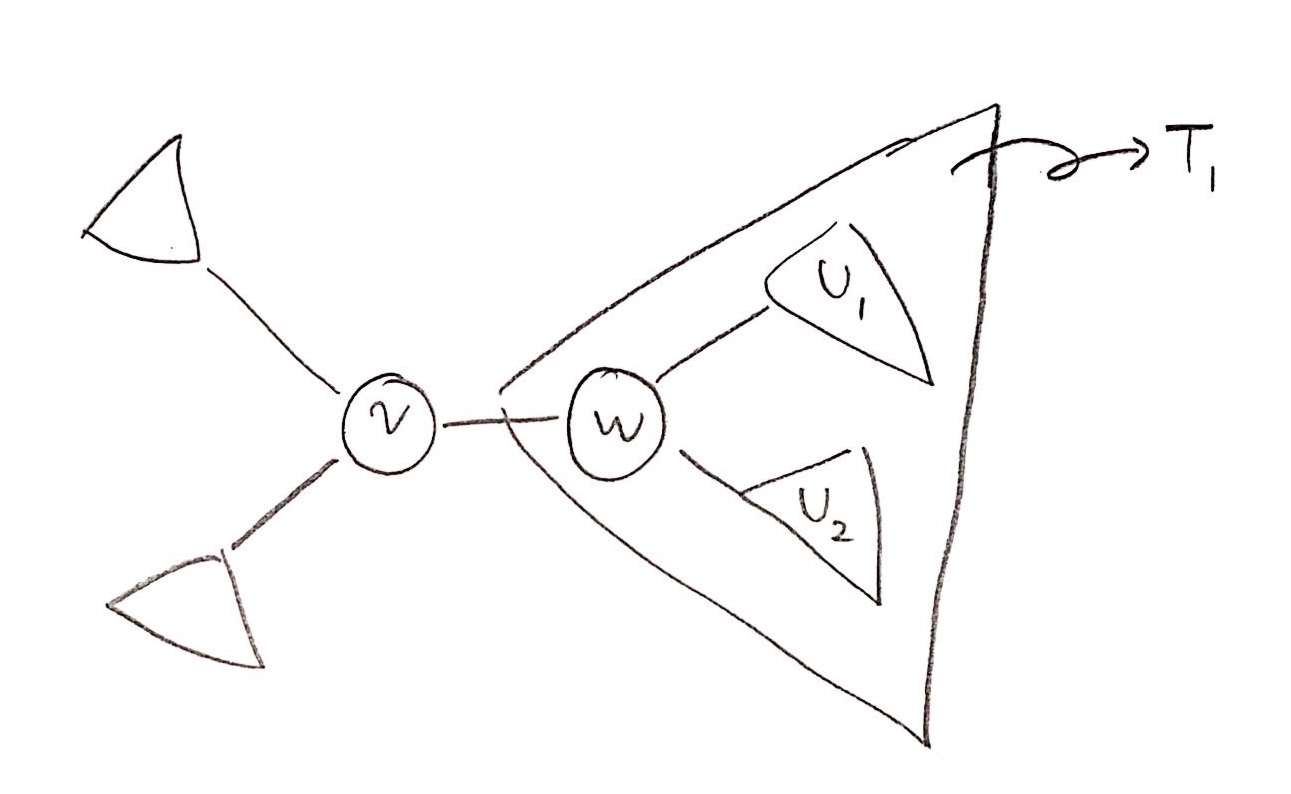
- 명제) 모든 트리에 대해 centroid는 존재한다.
- 증명) 모든 가능한 정점 중에, 서브트리 중 가장 큰 트리의 정점 수가 가장 작은 정점을 $v$라고 할 것이고, 이 중 가장 큰 서브트리를 $T_1$ 이라고 하자. 만약 centroid가 존재하지 않는다면, $ \vert T_1 \vert > \vert T \vert /2$ 일 것이다. $T_1$의 루트를 $w$라고 하자. 이 경우에 $w$의 서브트리를 보면, 원래 $T_1$이었던 부분과, $T_1$이 아니였던 부분으로 나뉠 수 있다. 이 $w$의 모든 서브트리는 $T_1$ 보다 크기가 작으므로 가정에 모순이다.
- 원래 $T_1$이었던 부분 $U_i$는 $T_1$의 서브트리이기 때문에, $T_1$보다 크기가 작다.
- 원래 $T_1$이 아니었던 부분 $V$의 크기는 $ \vert V \vert = \vert T \vert - \vert T_1 \vert < \vert T \vert - \vert T \vert /2 = \vert T \vert /2$ 이므로 $T_1$ 보다 크기가 작다.
또한 이 centroid는 서브트리의 크기를 구해주는 동적계획법을 적용해서 간단하게 찾아줄 수 있다.
이 centroid를 통해서 분할정복으로 이 문제를 해결 할 수 있다.
시간 복잡도는 $O( \vert T \vert \log \vert T \vert )$ 이다.
C - Islands
문제
정수 $n$에 대해, 1 이상 $n$이하의 정수로 이루어진 두 순열 ${A_i}$와 ${B_i}$가 원 위에 주어진다. 우리는 어떠한 순열 ${C_i}$를 찾아야 하는데, 두 원에 $C_1$과 $C_2$를 잇는 선분, $C_2$와 $C_3$를 잇는 선분, …, $C_{n-1}$과 $C_n$을 잇는 선분을 그렸을 때, 모든 원에 대해서 임의의 두 선분이 (양 끝점을 제외하고) 교차하면 안된다.
이러한 $C_i$가 존재하면 찾고, 존재하지 않으면 존재하지 않는다고 출력하여라.
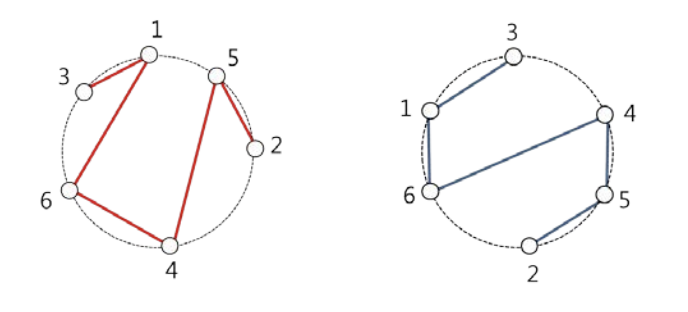
그림 설명: $A = (1, 5, 2, 4, 6, 3), B = (3, 4, 5, 2, 6, 1), C = (3, 1, 6, 4, 5, 2)$이다.
풀이
어떤 점 $u$에서 시작하는 경로가 있다고 하자. 그리고 이 경로가 현재까지 $u=p_1, p_2, \cdots, p_k$를 지났다고 하자. 그럼 $A$에서도 $B$에서도 $p_1, \cdots, p_k$는 연속된 구간을 이루어야 한다. 만약 그렇지 않다고 하면 $p_k$가 지나야 할 서로 연결되어있지 않는 구간의 갯수가 2개 이상이 되고, 이 둘을 지나는 선분은 $p_{k-1}$과 $p_k$를 잇는 선분과 교차할 것이기 때문이다.
그렇기 때문에, 우리는 다음의 $O(N^2)$풀이를 얻을 수 있다.
- 모든 정점 $u$를 시도해 본다. $p_1=u$라고 하고, 다음을 반복한다.
- 현재 방문한 경로에 대해서 $A$에서도 연속된 구간의 양 끝이면서, $B$에서도 연속된 구간의 양 끝인 점이 있으면, 그 점을 경로에 추가한다. (두개 이상일 경우 아무거나 택해도 된다. 왜냐하면, 결론적으로 그 두 점이 모두 경로에 포함될 수 있기 때문이다.)
- 모든 점이 경로에 추가 되었으면 $u$는 답이다.
여기서 우리는 다음과 같은 과감한 휴리스틱을 하나 시도 할 것이다.
- 위의 방법으로 한번이라도 방문 된 점에 대해서는 두 번 시도하지 않는다.
가령, 위 풀이에서 5->3->4을 시도 하고, 답이 아니라는 결론을 얻었으면, 3과 4에서는 시작해 보지 않아도 된다는 것이다. 이 풀이가 올바르다는 것과 효율적이라는 ($O(N)$) 것을 증명 할 것이다.
- (명제) 이 풀이는 올바르다.
- $i$에서 $j$에 도달할 수 있고, $j$를 정답으로 하는 답이 있다면, $i$에서 $j$로 오는 수열과 $j$에서의 정답 중 $i$에서 $j$로 오는 수열의 원소를 제외하고 이어 붙인 새로운 수열 $C$가 $i$에서 시작하는 정답이라는 것을 어렵지 않게 보일 수 있다. 즉 $i$에서 시도 해 보았을 때 정답이 아니라면, $j$에서 시도 해 볼 필요는 없다.
- (명제) 이 풀이는 $O(N)$이다.
- 어떤 점 $i$에 접근 하기 위해서는 $A$쪽에서 인접한 두 점과 $B$쪽에서 인접한 두 점 중 하나, 혹은 해당하는 점에서 시작하는 방법을 통하여 접근 해야 하므로, 점 $i$에 중복 없이 접근 하는 방법은 총 5가지 이고, 이 이외의 경우에는 접근 하는 방식이 없다.
D - Ladder Game
문제
(원문은 사다리 타기이고, 지문이 잘못 쓰였기 때문에 엄밀하게 바꾸었다.)
길이 $L$의 $1$ 이상 $n-1$ 이하의 정수로 이루어진 수열 $A$ 가 주어진다. 우리는 순열 $\pi_A$ 를 다음과 같이 정의할 것이다: $\pi = (1, 2, \cdots, n)$에서 시작하여, 총 $L$번의 단계로 순열을 섞는데, $\pi$의 $A_i$ 번째 원소와 $A_{i+1}$ 번째 원소를 섞는다.
수열 $A$의 부분 수열 $B$가 $\pi_B = \pi_A$를 만족 하면서, 어떤 다른 $B$의 부분 수열 $C$에 대해서도 $\pi_C = \pi_B$를 만족하지 않는 부분 수열 $B$를 우리는 “극소 순열” 이라고 할 것이다. 이러한 극소 수열을 아무거나 하나 찾아 출력하여라. ($3 \le n \le 50, 0 \le L \le 25000$, 실제 대회에 사용된 데이터는 $n$과 $L$이 작았다.)
풀이
어떤 순열 $\pi$의 inversion을 $i < j$ 이고 $\pi_i > \pi_j$인 순서쌍 $(i, j)$의 갯수라고 정의할 것이다. 인접한 두 원소를 교환하는 연산은 inversion을 1 증가시키거나 1 감소시킨다. 왜냐하면, $(i, i+1)$이 inversion에 포함되는지 안되는지의 여부가 달라지고 $(, i)$의 순서쌍은 $(, i+1)$ 로, $(, i+1)$의 순서쌍은 $(, i)$로 이동하기 때문이다.
$\pi_A$를 만드는 $A$의 부분수열 $B$의 최소 길이는 $\pi_A$의 inversion의 갯수보다 크다 라는 사실을 알 수 있다. 한 번 순열을 섞을 때 inversion을 1씩밖에 증가시키지 못하기 때문이고, 원래 순열의 inversion은 0이기 때문이다.
이제 부분수열 $B$를 명시적으로 찾을 것이다. $A$에서 필요 없는 두 원소를 없애가면서 부분수열을 찾을 것이다. $A$에서 위와 같은 방법으로 $\pi_A$를 만들 때, inversion을 감소 시키는 수를 $A_x$라고 하자. (즉, $x-1$번 연산을 진행하고, $\pi$의 $A_x$번째 원소 $L$과 $A_{x+1}$번째 원소 $R$를 비교해 봤을 때, $A_x$번째 원소가 더 컸다고 하자.) 이후, 이전 과정에서 $R$과 $L$을 바꾼 적이 있었고, 이 둘을 제거한 부분 수열은 같은 $\pi$를 만든다.
원래 수열에서는, 작은 수가 항상 왼쪽에 있기 때문에 $R$이 왼쪽에 있고, $L$이 오른쪽에 있을 것이다. 섞는 일련의 과정에서 $R$이 오른쪽, $L$이 왼쪽으로 갔다는 뜻은 중간에 $R$과 $L$의 경로가 교차하는 $A_y$가 있었다는 뜻이다. $A_y$와 $A_{y-1}$의 차이는 $L$과 $R$이 바뀐 것이고, 이 이후 $y+1$번째 부터 $x-1$번째 연산까지 진행 해도, 두 수열은 $L$과 $R$만 바뀐 것이고, 추가로 $x$번째 연산을 시행 해 주면 $L$과 $R$이 두번 바뀌었기 때문에 원래 위치로 돌아오며, 같은 수열인 $\pi$를 만든다.
이 연산은 수열의 길이만큼 시행 할 수 있고, 찾는 시점은 inversion이 감소할 수 있는 시점인 $n^2$번째 시점이기 때문에 시간 복잡도는 $O(n^2 \times L)$ (문제에서는 $O(n^2 \times nl)$) 이다.
E - Network Vulnerability
문제
그래프 $G$의 $c_k(G)$를, $G$에서 $k$개의 정점을 제거 했을때 나뉘어지는 그래프 연결 성분의 최대 갯수라고 정의 하자.
구간 $n$개로 이루어진 구간 그래프 $G$가 주어졌을 때, $c_1(G), c_2(G), \cdots, c_{n-1}(G)$를 구하여라. 여기서 구간 그래프란, 각 구간을 하나의 정점으로 하며, 두 구간 $x$와 $y$가 교차하면 $x$와 $y$사이에 선분이 존재하는 그래프를 의미한다.
풀이
구간들을 전처리를 통해서, 같은 구간그래프를 만들면서 좌표가 1이상 N+1이하가 되도록 줄여줄 수 있다. 또한, 구간의 왼쪽 끝 점을 기준으로 구간을 정렬해 주자. 여기서 우리는 다음과 같은 동적계획법을 돌릴 것이다.
$dp_{i, j, k}=$ 0번째 부터 $i$번째 구간까지 고려를 했을 때, 그래프 연결 성분의 갯수가 $j$개가 되면서, 이 구간의 마지막 끝 점이 $k$인 조건을 만족하면서 넣을 수 있는 최대 연결 성분의 갯수
초기 조건은, $dp_{-1, 0, 0} = 0$ 이다.
이 때, $i+1$번째 구간의 시작점을 $L$, 마지막 점을 $R$이라고 하고, $L$이 가장 오른쪽 연결성분의 시작점 보다 오른쪽에 있음을 유의하면, 다음과 같은 동적계획법 점화식을 세울 수 있다. $a \rightarrow b$를 “$b$가 $a$를 부분해로 가지기 때문에, $b = max(b, a)$로 계산된다.” 로 정의하겠다.
- $D_{i, j, k} \rightarrow D_{i+1, j, k}$
- 이 경우는, $i+1$번째 구간을 사용하지 않은 경우이다.
- $k < L$: $D_{i,j,k}+1 \rightarrow D_{i+1,j+1,R}$
- 이 경우는, 마지막 연결성분보다 시작점이 오른쪽에 있는 경우이기 때문에, 새로운 연결성분이 만들어지게 된다. (2번째 성분이 $j+1$이 된다.) 또한, 이 때 오른쪽 끝 점은 $R$이 된다.
- $ L \le k$: $D_{i,j,k} +1 \rightarrow D_{i+1, j, max(k, R)}$
- 이 경우는, 마지막 연결성분보다 시작점이 같거나 왼쪽에 있는 경우이기 때문에, 새로운 연결성분이 만들어지지 않고, (2번째 성분이 $j$이다.) 이 때 오른쪽 끝 점은, 기존의 값인 $k$와, 새 구간인 $R$중 최댓값이 된다.
이 동적계획법 테이블을 그대로 계산한 후 최적화를 해 주면 $O(N^3)$의 시간에 문제를 해결할 수 있다. $i+1$번째 동적계획법 식은 $i$번째만 이용하기 때문에, DP테이블을 $i$번째와 $i+1$번째만 들고 있는 것과, $i+1$번째에서 값이 크게 바뀌는 것이 $D_{i+1, *, R}$ 인 점 등을 이용하여 최적화를 해 주면 문제를 해결하기에 충분하다. 또한, Segment tree with lazy propagation등을 사용하여 최적화를 하여서 $O(N^2 \log N)$에 문제를 해결할 수도 있다.
F - Quadrilaterals
문제
평면 위에 $n$개의 점이 있다. 이 $n$개의 점으로 만들 수 있는 사각형들 각각의 점수를 매길 것이다. 사각형 중 최소 넓이를 $a$ 라고 할 때,
- 크기가 $a$인 볼록 다각형은 4점
- 크기가 $a$인 오목 다각형은 3점
- 크기가 $a$보다 큰 볼록 다각형은 2점
- 크기가 $a$보다 큰 오목 다각형은 1점
이다. 가능한 모든 사각형의 점수의 합을 구하여라 ($4 \le n \le 1000$, 세 점은 한 직선 위에 있지 않다.)
풀이
이 문제는 볼록 다각형에 2점, 오목 다각형에 1점을 주고, 크기가 최소 넓이와 같은 사각형 당 점수를 2점 주어서, 이를 모두 더하는 문제이다.
이는, 볼록 다각형과 오목 다각형의 갯수를 세는 부분과, 크기가 최소 넓이와 같은 사각형의 점수를 세는 부분으로 문제를 나누어서 풀 수 있다.
일단 우리는 이 둘을 위해서, 원점에서 $x$축과 특정한 각도 $\theta$만큼 차이가 나는 직선 $L$을 그어서, 점들을 $L$에 사영시킨 순서 대로, 정렬을 할 것이고, 이를 모든 $0 \le \theta < \pi$를 만족하는 $\theta$에 대해 할 것이다.
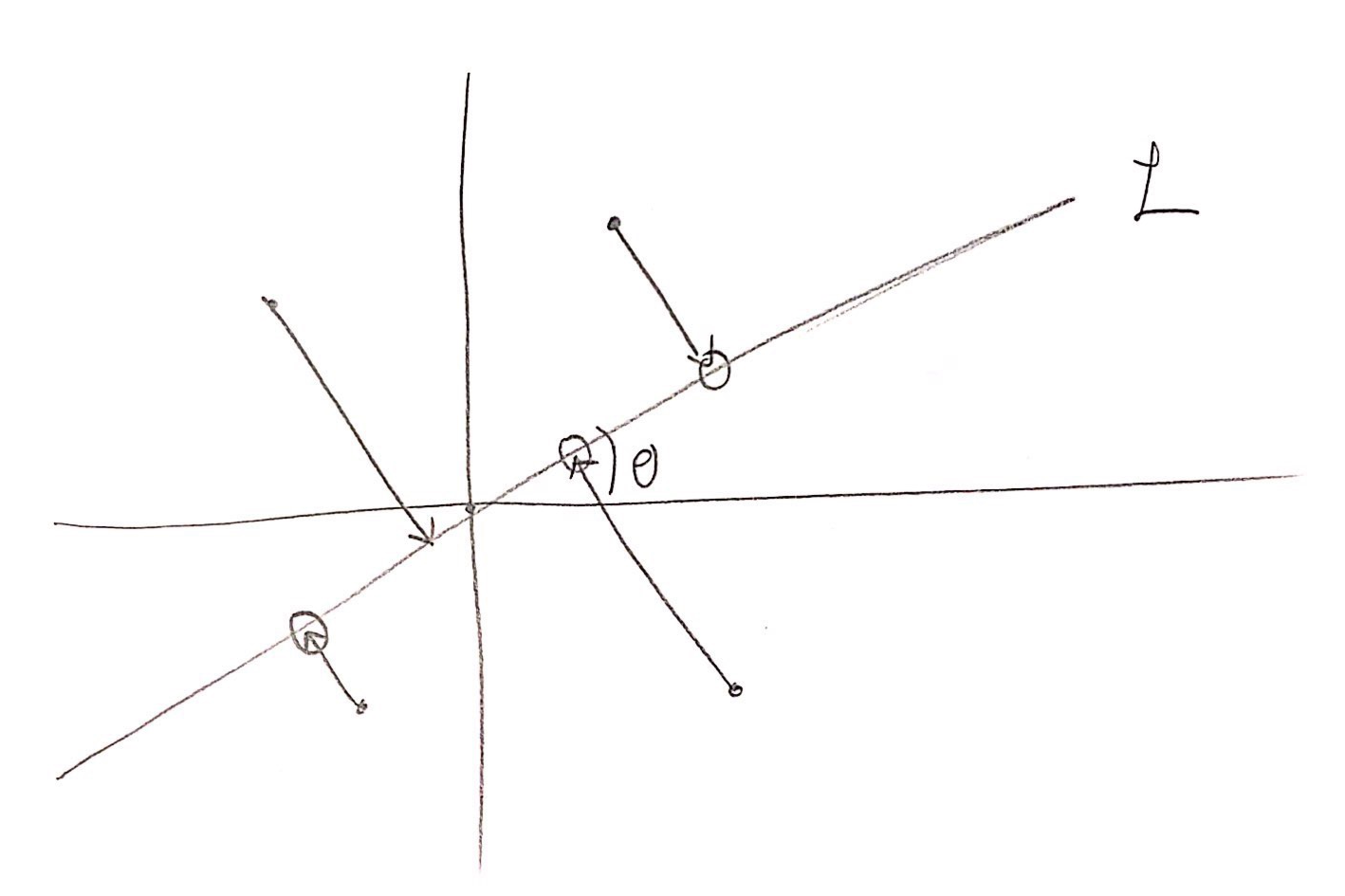
우리는 이 $\theta$를 늘려가는 과정에서, 정렬 순서가 변하는 위치가 많아봐야 $n(n-1)/2$번 이라는 사실을 알 수 있다. 왜냐하면, 정렬 순서가 바뀌기 위해서는 $L$에 사영된 두 점 $proj_L x$, $proj_L y$가 서로 만나야 한다. 이 두 점은 $\pi$만큼 돌아가는 과정에서 최대 한번 밖에 만나지 않기 때문에 ($x-y$ 선분과 $L$이 수직이 될 때), 그리고 순서쌍의 갯수보다 적게 바뀐다는 것을 알 수 있다. 또한 이러한 정렬 순서에서는 두 점 $x$, $y$의 순서가 바뀌며, 직선 $x-y$와의 거리를 기준으로 나머지 점이 정렬된다는 것을 알 수 있다. 이 정렬은 모든 순서쌍에 대해서 $n(n-1)/2$개의 각도를 정렬해 주는 방식으로 구현할 수 있으며, $O(n^2 \log n)$의 시간이 걸린다.
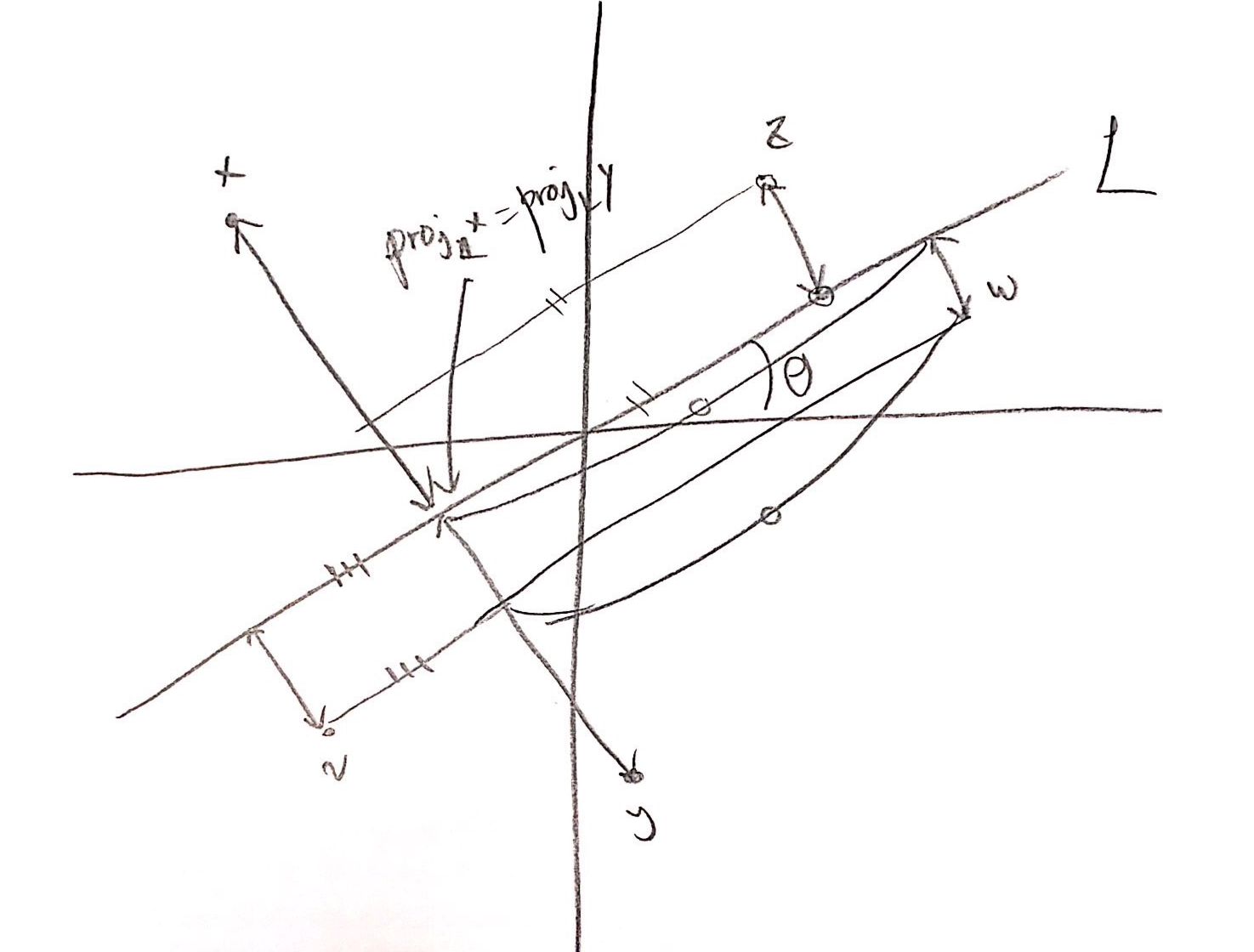
우리는 또한, 볼록다각형과 오목다각형을 구분하는 방법에 대해, 대각선의 갯수에 대해서 볼 것이다. 볼록 다각형은 대각선의 갯수가 2개이고, 오목다각형은 대각선의 갯수가 1개이다. 즉 다각형에 대한 점수는 대각선의 갯수에 대한 점수와 동일하기 때문에, 선분 $x-y$를 대각선으로 하는 사각형은 $x-y$의 한쪽 평면에 있는 점과 다른쪽 평면에 있는 점 두개를 집어서 만들 수 있기 때문에, 양 반평면의 점 갯수의 곱과 같고, 이를 더해 주면 볼록다각형과 오목 다각형에 대한 점수를 계산할 수 있다. 또한, $x-y$를 대각선으로 하는 사각형을 세어 줄 때, 양쪽 반평면에서 $x-y$와 가장 까운 점들에 대해서만 고려를 하면 된다. 이를 구현 해 주면 총 $O(n^2 \log n)$시간에 문제를 해결할 수 있다.
G - Same Color
문제
수직선 상에 $n$개의 정점에 각각 색이 칠해져 있다. 우리는 이 점들의 집합을 $S$라고 한다.
우리는 다음 성질을 만족하는 어떤 공집합이 아닌 $S$의 부분집합 $C$를 고려할 것이다.
- 모든 $S$ 에 있는 점 $p$에 대해서, $p$의 색과, $C$에 있는 점 중 $p$와 가장 가까운 점과의 색이 같다. (가장 가까운 것이 여러개 있을 경우 하나만 색이 같아도 된다.
이러한 부분집합 $C$중에 크기가 제일 작은 부분집합의 크기를 구하여라.
풀이
$D[i]$를 집합 $S$를 좌표 순으로 정렬 했을 때 1번 부터 $i$번 까지의 점에 대해서 문제를 풀었을 때, 부분집합 $C$의 크기 중 가장 작은 것의 크기라고 하자.
우리는 점들을 연속된 같은 색끼리 고려 할 것이다. 이 점들의 필요조건 중 하나는, 연속된 구간 중 적어도 하나에는 점이 존재해야 한다는 것이다. 존재하지 않은 경우에는, 존재하지 않는 구간의 가장 첫 점이 문제의 조건을 만족하지 않게 된다.
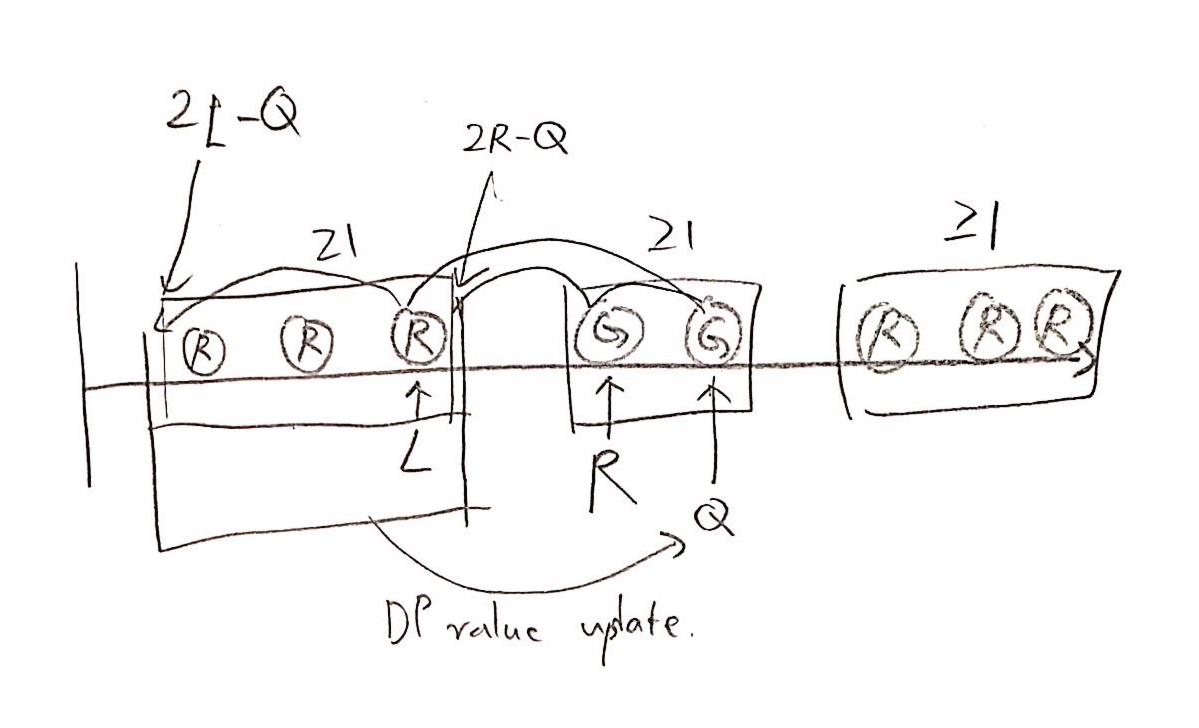
처음 연속된 구간의 $D[i]$값이 1인 것은 자명하다. ($i$번째 점 하나를 원소로 하는 집합 $C$를 만들면 된다.) 우리는, 이전 구간에 $C$에 속해 있는 점이 $P$위치에 찍혔고, 이전 구간의 점이 $L$위치에서 끝나고 현재 구간의 점이 $R$위치에서 시작하며, 우리가 $C$에 넣을 것을 고려하고 있는 점이 ($D[Q]$를 구하는 점이) $Q$라고 하면, 이전 구간의 점은 이전 구간에 속해야 하므로 $L-P \ge Q-L$ 이고, 현재 구간의 점은 현재 구간에 속해야 하므로 $Q-R \ge R-P$ 이어야 한다. 이 조건을 만족하는 $P$들을 two pointer나 이분탐색 등으로 찾아서, 이 $P$들 중 최솟값 + 1로 $D[Q]$를 정해주면 되고, 이를 위해서 deque나 세그먼트 트리 등을 활용 할 수 있다.
시간 복잡도는 둘 다 $O(n)$시간인 two pointer와 deque를 쓰면 $O(n)$이고, 아닌 경우에는 $O(n \log n)$이다. 작성한 코드에서는 two pointer와 세그먼트 트리를 사용했다.
H - Strike Zone
문제
평면 상에 점으로 이루어진 두 집합 $P_1$과 $P_2$가 있다. 직사각형 $R$에 대해, $R$에 속해 있는 $P_1$의 점 갯수를 $s$, $P_2$의 점 갯수를 $b$라고 할 경우, 주어진 수 $c_1, c_2$에 대해 $eval(R) = c_1 s - c_2 b$라고 정의 하자. eval의 값이 최대가 되는 직사각형을 찾아서 $eval(R)$을 구하여라. ($1 \le \vert P_1 \vert , \vert P_2 \vert \le 1000$
풀이
직사각형의 아랫쪽 끝과 위쪽 끝을 고정시켜 놓으면, 최대 부분 구간합 구하기 문제가 된다. 즉, 아랫쪽 끝을 고정시켜 놓고 위쪽 끝을 올려가면서 새로 추가되는 점들을 구하면, 최대 부분 구간합 구하기 문제를, 수열에 숫자가 갱신되는 버전으로 풀어야 한다.
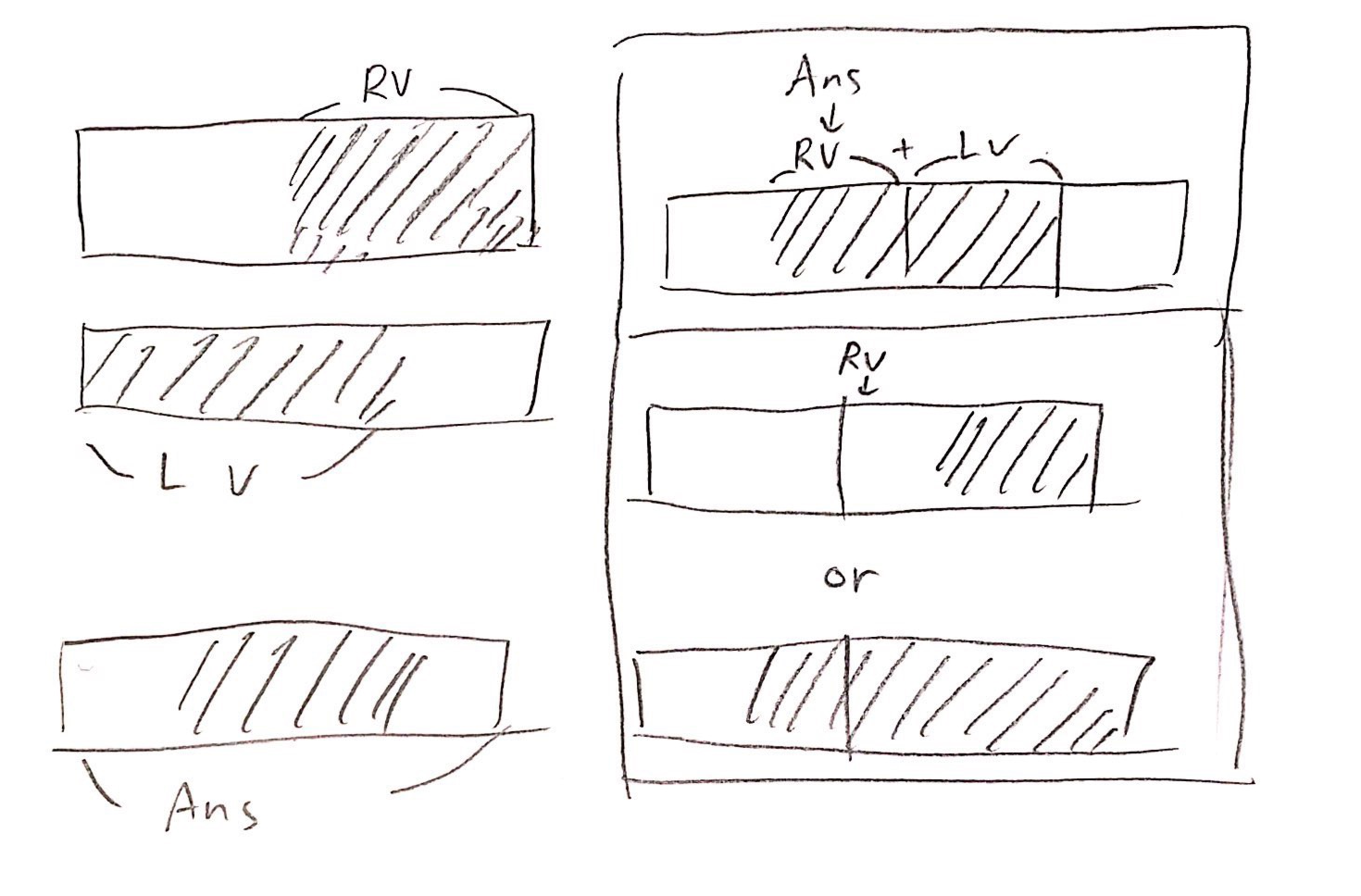
우리는 어떤 부분 구간합 문제를 분할정복으로 푸는 방법을 제시 할 것이다. 왼쪽 구간과 오른쪽 구간의 정보를 가지고, 양쪽 구간의 정보를 합쳐서 새로운 구간의 정보를 구하는 방식이다. 우리는 이를 위해서, 최대 부분 구간합, 왼쪽 누적합중 최댓값, 오른쪽 누적합 중 최댓값, 전체 구간의 합이 필요하다.
- 최대 부분 구간합은, 양쪽의 최대 부분 구간합, 혹은 가운데를 포함하는 최대 부분 구간합 중 하나이다. 즉 max(왼쪽의 최대 부분 구간합, 오른쪽의 최대 부분 구간합, 왼쪽의 오른쪽 누적합 중 최대값, 오른쪽의 왼쪽 누적값중 최댓값) 이다.
- 왼쪽 누적합중 최댓값은, 왼쪽의 누적합중 최댓값이거나, 오른쪽 까지 고려가 되어있어야 하므로 max(왼쪽의 왼쪽누적합 중 최댓값, 왼쪽의 합 + 오른쪽의 왼쪽 누적합 중 최댓값) 이다.
- 오른쪽 누적합도 마찬가지로 하면 된다.
- 합은 왼쪽의 합 + 오른쪽의 합이다.
이 방식을 세그먼트 트리와 합쳐서 사용 할 경우 각 (아랫쪽 끝 위치, 위쪽 끝 위치)의 순서쌍 마다 $O(\log n)$ 시간에 계산할 수 있어서 총 $O(n^2 \log n)$시간에 답을 구할 수 있다.
I - Thread Knots
문제
구간이 $n$개 주어진다. 이 구간은 어떤 두 구간도 서로 포함하지 않는다. 이 $n$개의 구간 각각 마다 정수 좌표점중 하나에 표시를 할 것이다. 이 표시 $n$개 중 가장 가까운 두 표시의 거리로 가능한 값 중 최댓값을 구하여라. ($1 \le n \le 100000$)
풀이
이분탐색을 사용 하면, 문제가 결정문제로 바뀐다. 즉 답으로 $L$이 가능한지 불가능 한지 확인 해 본다. $L$에서 가능하면 $L-1$에서도 당연히 가능하고, 마찬가지로 $L$에서 불가능하면 $L+1$에서 불가능하기 때문에, 이를 이진탐색으로 찾을 수 있다.
답을 $L$로 고정 시키자. 구간에 표시를 할 때는 구간의 왼쪽 끝(=오른쪽 끝) 순으로 정렬을 한 뒤에, 왼쪽 부터 보면, 항상 표식을 가장 놓을 수 있는 왼쪽에 놓는게 이득이다. 왜냐하면, 오른쪽에서 가능한 답이 있다면, 표식들을 왼쪽으로 가능한한 왼쪽으로 당겨서 새로운 답을 만들 수 있기 때문이다.
즉, 이전 표식을 단 위치가 $V$이고, 현재 구간이 $[S, E]$를 보고 있으면, 표식을 달 수 있는 가장 왼쪽 위치는 $min(V+L, S)$이고, 이것이 $E$초과인지 아닌지 확인 해 준 다음에 $V$를 $min(V+L, S)$로 갱신해주면 된다.
시간 복잡도는 정렬을 하는데 사용하는 $O(n \log n)$이다.
J - Triangulation
문제
정$n$각형은 서로 교차하지 않는 대각선 $n-2$개를 추가하여 $n-2$개의 삼각형으로 삼각분할 할 수 있다. 이 때, 두 삼각형이 인접해 있는 (거리 1인) 것을, 두 대각선이 맞닿아 있다고 생각하자. 임의의 두 삼각형 $a$와 $b$의 거리는 $a$에서 시작하여 인접한 삼각형들을 통해서 $b$로 도착하는데에 드는 최소한의 삼각형의 갯수이다.
삼각분할의 지름을 삼각형에서 가장 거리가 먼 두 삼각형 사이의 거리라고 정의 할 때, 정 $n$각형을 지름이 최소가 되도록 삼각분할 하면 거리는 몇인가?
풀이
정 $n$각형과, 모든 정점의 차수가 3 이하인 트리는 동치이다.
이 트리의 중심(지름의 중점)은 변 위, 혹은 한 점에 있을 수 있다.
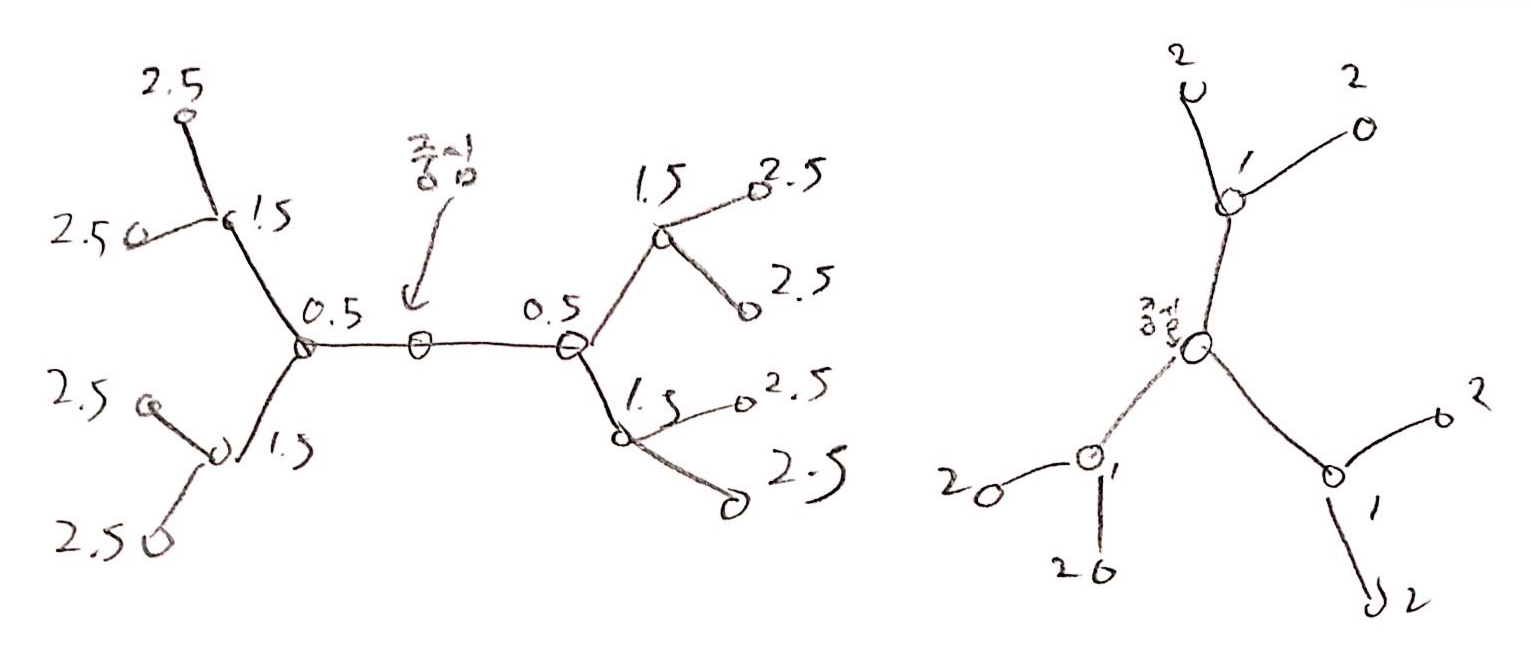
한 점으로 부터 거리가 $k$이하인 점을 만들기 위해서는, 정점을 가능한 최대 차수만큼 추가해야 한다.
한 점이 중심일 때는, 거리가 $k$이하인 점을 추가하면 $1+3\times 2^0 + 3\times 2^1 +\cdots + 3 \times 2^{k-1}$만큼의 정점이 생기고, $3 \times 2^k -2$ 가 지름 $2k$로 가능한 최대 정점 갯수이다.
변의 중점이 중심일 때는, 거리가 $k+0.5$이하인 점을 추가하면 $2+ 2\times 2^0 + 2\times 2^1 + \cdots + 2 \times 2^k$ 만큼의 정점이 생기고, $4 \times 2^k -2$가 지름 $2k+1$로 가능한 최대 정점 갯수이다.
즉, $3 \times 2^k$각형은 지름 $2k$로, $4\times 2^k$각형은 지름 $2k+1$로 삼각분할 될 수 있으며, 주어진 $n$에 대해서는 $k$를 1씩 늘려가면서 찾으면 된다. 이런 경우 시간복잡도 $O(\log k)$ 정도의 시간에 쉽게 찾을 수 있다.
K - Washer
문제
$n$개의 색 $(r_i, g_i, b_i)$들에 대해서, $r_i,g_i, b_i$들의 평균을 각각 $r, g, b$라고 했을 때, 색 이동을 $\sum_{i=1}^n (r_i-r)^2 + (g_i-g)^2 +(b_i-b)^2 $ 이라고 정의하자.
$n$개의 색 $(r_i, g_i, b_i)$가 주어질 때, 이 수들을 $k$개의 집합으로 나누어서, 각 집합의 색 이동의 합의 최솟값을 구하여라. ($1 \le n \le 100, 1 \le k \le 2$, 점들은 세 점이 한직선 위에 있거나 네 점이 한 평면위에 있지 않음)
풀이
$k=1$일 때는 그냥 식을 계산해 주면 된다. 그래서 우리는 $k=2$ 일 때만 풀 것이다.
색 이동의 합이 최소가 되는 두 집합을 $S_1,S_2$라고 하고, 이들의 평균을 $R_1, G_1, B_1$과 $R_2, G_2, B_2$라고 할 것이다. 우리는 $S_1$에 속해 있는 모든 점은 $R_1, G_1, B_1$으로 부터의 거리가 $R_2, G_2, B_2$로 부터의 거리보다 가깝거나 같고, $S_2$에 속해 있는 점도 마찬가지로 $R_2, G_2, B_2$로 부터의 거리가 $R_1, G_1, B_1$으로 부터의 거리보다 가깝거나 같다라는 사실의 주목할 것이다.
이는 가령이면, $S_1$에 $R_2, G_2, B_2$와의 거리가 더 가까운 점 $(r, g, b)$가 있다고 하자. 이 경우에, $(r, g, b)$를 집합 $S_1$에서 $S_2$로 옮겨 주면, $((r-R_1)^2 + (g-G_1)^2+(b-B_1)^2) - ((r-R_2)^2 + (g-G_2)^2+(b-B_2)^2)$ 만큼 color transfer가 줄어든다는 사실을 알 수 있다. 이로 인해 평균이 바뀌어서 color transfer가 늘어나는 경우는 없다. 왜냐하면, color transfer $\sum_{i=1}^n (r_i-x)^2 + (g_i-y)^2 +(b_i-z)^2 $ 의 최솟값은 $x, y, z$가 각각 $r_i, g_i, b_i$들의 평균인 경우에 발생하기 때문이다. (간단한 이차함수의 전개를 통해 확인할 수 있다.)
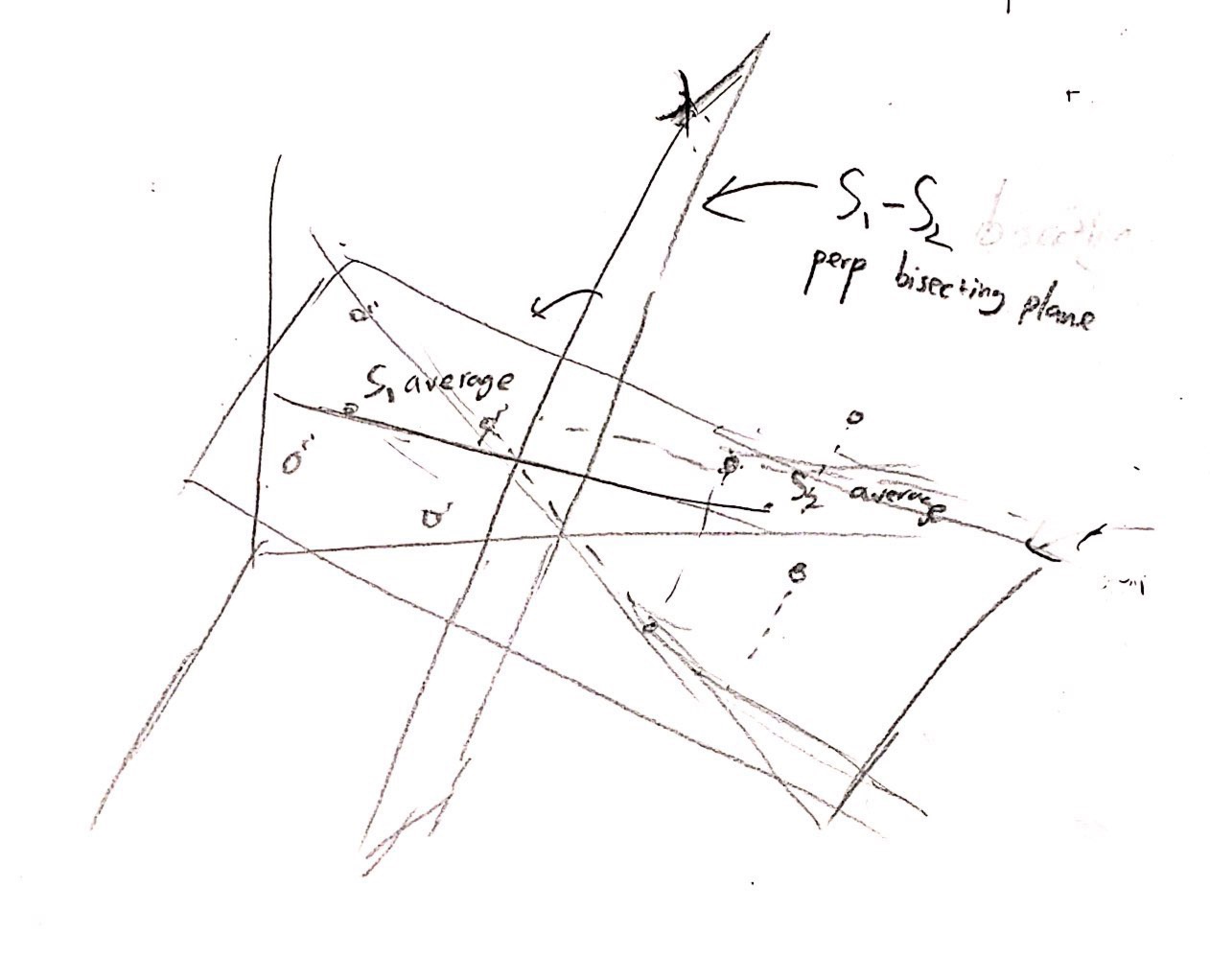
즉, 최적인 $S_1$과 $S_2$는 평면을 기준으로 나뉘어 진다. 이렇게 나뉘어진 평면을 $S_1$과 $S_2$에 닿게 기울여 주면, $N$개의 점 중 3개의 점으로 이루어진 평면으로 $S_1$과 $S_2$가 나뉘어 진다는 것을 알 수 있고, 평면이 $O(n^3)$개 존재하기 때문에 총 $O(n^4)$에 시간으로 문제를 해결할 수 있다.
평면에 어느쪽에 있는 지는, 평면의 법선벡터를 외적으로 구한 후 법선 벡터와 내적을 통해 값이 0 이상인지 아닌지에 따라 각도가 90도 이상인지 아닌지 알 수 있다.
L - What’s Mine is Mine
문제
광물들의 정보 $n$개가 주어진다. 이는 $(s, e, t)$로 주어지는데, $s$일에 시작해서 $e$일 까지 광물을 캘 수 있으며, 이 광물의 종류가 $t$라는 것이다. 이 광물의 가치는 별도로 주어진 배열 $A$에 대해, $c_t = (e-s) \times A_t$로 계산 된다.
여러 광물들을 캐려고 하는데, 광물 끼리 채굴하는 시간이 겹쳐서는 안된다. 광물들을 채굴하여 가치의 합을 최대화 하여 그 값을 출력하여라.
풀이
$D[i]$를 $i$일까지 일을 했을 때 번 돈의 최댓값이라고 정의하자. 이것은 두 가지 경우 중 하나이다.
- $i-1$부터 $i$일 까지 일을 하지 않았을 때 (혹은 일을 하고 있는 중일때): $D[i] = D[i-1]$
- $s$일에 시작하여 $i$일에 끝나는 일의 가치가 $c$일 때: $D[i] = D[s] + c$
동적 계획법 테이블을 채우면서, 이 중 최댓값을 골라가며 채우면 된다. 시간복잡도는 $O(n \log n)$이다.
코드
A
#include<bits/stdc++.h>
using namespace std;
int main()
{
int N; cin >> N;
vector<int> A(N+1, 1);
for(int i=2; i<=N; ++i)
{
set<int> S;
for(int k=1; i-2*k>=0; ++k)
S.insert(2*A[i-k]-A[i-2*k]);
for(int k=1;; ++k)
if(!S.count(k))
{
A[i] = k;
break;
}
}
cout << A[N] << endl;
return 0;
}
B
#include<bits/stdc++.h>
using namespace std;
set<pair<int, int> > conn[101010];
int deg[101010];
int sz[101010];
vector<int> nodes;
void dfs(int a, int pa)
{
nodes.push_back(a);
sz[a] = 1;
for(auto tmp: conn[a])
{
if(tmp.first==pa) continue;
dfs(tmp.first, a);
sz[a] += sz[tmp.first];
}
return;
}
int find_cen(int a)
{
nodes.clear();
dfs(a, 0);
int tot = sz[a];
for(auto x: nodes)
{
int v = tot-sz[x];
for(auto tmp: conn[x])
{
if(sz[tmp.first] < sz[x])
v = max(v, sz[tmp.first]);
}
if(v<=tot/2) return x;
}
}
vector<int> dists;
void dfs2(int a, int pa, int w)
{
for(auto tmp: conn[a])
{
int x, ww; tie(x, ww) = tmp;
if(x==pa) continue;
dfs2(x, a, w+ww);
}
if(deg[a] == 1) dists.push_back(w);
}
long long solve(int x)
{
if(deg[x] == 1) return 0LL;
vector<vector<int> > V;
vector<long long> sum;
vector<long long> squaresum;
for(auto tmp: conn[x])
{
dists.clear();
dfs2(tmp.first, x, tmp.second);
V.push_back(dists);
long long sv = 0, ssv =0;
for(auto x: dists)
{
sv += x;
ssv += 1LL*x*x;
}
sum.push_back(sv);
squaresum.push_back(ssv);
}
long long ans = 0;
for(int i=0; i<(int)V.size(); ++i)
for(int j=0; j<i; ++j)
ans += squaresum[i]*V[j].size() + squaresum[j]*V[i].size() + 2*sum[i]*sum[j];
return ans;
}
int main()
{
int N; cin >> N;
for(int i=0; i<N-1; ++i)
{
int u, v, w;
cin >> u >> v >> w;
conn[u].emplace(v, w);
conn[v].emplace(u, w);
++deg[u]; ++deg[v];
}
queue<int> Q;
Q.push(1);
long long ans = 0;
while(!Q.empty())
{
int x = Q.front(); Q.pop();
int y = find_cen(x);
ans += solve(y);
for(auto tmp: conn[y])
{
int a, w; tie(a, w) = tmp;
conn[a].erase(make_pair(y, w));
Q.push(a);
}
conn[y].clear();
}
cout << ans;
}
C
#include<bits/stdc++.h>
using namespace std;
int N;
vector<int> A, B;
vector<int> invA, invB;
int main()
{
scanf("%d", &N);
A.resize(N); B.resize(N);
invA.resize(N); invB.resize(N);
for(int i=0; i<N; ++i)
{
scanf("%d", &A[i]);
--A[i];
invA[A[i]] = i;
}
for(int i=0; i<N; ++i)
{
scanf("%d", &B[i]);
--B[i];
invB[B[i]] = i;
}
auto inc=[&](int x)
{
++x; if(x==N) x=0; return x;
};
auto dec=[&](int x)
{
--x; if(x==-1) x=N-1; return x;
};
vector<bool> tried(N, false);
for(int s=0; s<N; ++s)
{
if(tried[s]) continue;
tried[s] = true;
vector<int> log;
int Alo, Ahi, Blo, Bhi;
Alo = Ahi = invA[s];
Blo = Bhi = invB[s];
bool flag = true;
log.push_back(s);
while(log.size() != N)
{
int t = log.back();
int AL = A[dec(Alo)], AR = A[inc(Ahi)];
int BL = B[dec(Blo)], BR = B[inc(Bhi)];
if(AL == BL)
{
Alo = dec(Alo); Blo = dec(Blo);
log.push_back(AL);
tried[AL] = true;
}
else if(AL == BR)
{
Alo = dec(Alo); Bhi = inc(Bhi);
log.push_back(AL);
tried[AL] = true;
}
else if(AR == BL)
{
Ahi = inc(Ahi); Blo = dec(Blo);
log.push_back(AR);
tried[AR] = true;
}
else if(AR==BR)
{
Ahi = inc(Ahi); Bhi = inc(Bhi);
log.push_back(AR);
tried[AR] = true;
}
else
{
flag = false; break;
}
}
if(flag)
{
for(auto x: log) printf("%d ", x+1);
puts("");
return 0;
}
}
puts("-1");
return 0;
}
D
#include<bits/stdc++.h>
using namespace std;
vector<int> ladder[1010];
map<pair<int, int>, pair<int, int> > name;
int perm[50];
pair<int, int> swapv[50][50];
int main()
{
int N;
scanf("%d", &N);
for(int i=0; i<N-1; ++i)
{
int cnt = 0;
while(true)
{
int t; scanf("%d", &t);
if(t==0) break;
ladder[t].push_back(i);
name[make_pair(t, i)] = make_pair(i+1, ++cnt);
}
}
{
LOOP:
for(int i=0; i<N; ++i) perm[i] = i;
for(int t=1; t<=1000; ++t)
{
for(int i=0; i<(int)ladder[t].size(); ++i)
{
int x = ladder[t][i];
int leftv = perm[x];
int rightv = perm[x+1];
if(leftv<rightv)
{
swapv[leftv][rightv] = make_pair(t, i);
swap(perm[x], perm[x+1]);
}
else
{
ladder[t].erase(ladder[t].begin()+i);
int ft, fi;
tie(ft, fi) = swapv[rightv][leftv];
ladder[ft].erase(ladder[ft].begin()+fi);
goto LOOP;
}
}
}
}
int cnt = 0;
for(int t=1; t<=1000; ++t) cnt += (int)ladder[t].size();
printf("%d\n", cnt);
for(int t=1; t<=1000; ++t)
{
for(int x: ladder[t])
{
int a, b; tie(a, b) = name[make_pair(t, x)];
printf("%d %d\n", a, b);
}
}
return 0;
}
E
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2048;
int N;
pair<int, int> interval[MAXN];
int dp[MAXN][MAXN];
int dpR[MAXN]; // dp[*][R]
int main()
{
vector<int> RP;
scanf("%d", &N);
for(int i=0; i<N; ++i)
{
scanf("%d%d", &interval[i].first, &interval[i].second);
RP.push_back(interval[i].second);
}
RP.push_back((int)-1e9-1);
RP.push_back((int)-1e9);
sort(RP.begin(), RP.end());
RP.resize(unique(RP.begin(), RP.end()) - RP.begin());
for(int i=0; i<N; ++i)
{
interval[i].first = lower_bound(RP.begin(), RP.end(), interval[i].first) - RP.begin();
interval[i].second = lower_bound(RP.begin(), RP.end(), interval[i].second) - RP.begin();
}
sort(interval, interval+N);
memset(dp, 0xaf, sizeof dp);
dp[0][0] = 0;
int maxcomp = 0;
for(int i=0; i<N; ++i)
{
int L = interval[i].first, R = interval[i].second;
for(int j=0; j<=maxcomp+1; ++j)
dpR[j] = dp[j][R];
for(int j=0; j<=maxcomp; ++j)
{
int val = dpR[j+1];
for(int k=0; k<L; ++k)
val = max(val, dp[j][k]+1);
dpR[j+1] = val;
val = dpR[j];
for(int k=L; k<R; ++k)
val = max(val, dp[j][k]+1);
dpR[j] = val;
for(int k=R; k<(int)RP.size(); ++k)
dp[j][k] += 1;
}
if(dpR[maxcomp+1] > 0) ++maxcomp;
for(int j=0; j<=maxcomp; ++j)
dp[j][R] = max(dp[j][R], dpR[j]);
}
vector<int> res(N+1);
for(int i=0; i<=N; ++i)
for(int j=0; j<(int)RP.size(); ++j)
res[i] = max(res[i], dp[i][j]);
for(int i=0; i<=N-1; ++i)
{
int comp = N-i;
for(int j=comp; j>=1; --j)
{
if(res[j] >= comp)
{
printf("%d ", j);
break;
}
}
}
puts("");
return 0;
}
F
#include<bits/stdc++.h>
using namespace std;
int N;
int X[1010];
int Y[1010];
long long ccw(int a, int b, int c)
{
long long bx = X[b]-X[a];
long long by = Y[b]-Y[a];
long long cx = X[c]-X[a];
long long cy = Y[c]-Y[a];
return bx*cy-cx*by;
}
int sgn(long long x)
{
if(x<0) return -1;
if(x==0) return 0;
return 1;
}
long long solve()
{
vector<pair< int, int> > slopes;
for(int i=0; i<N; ++i)
for(int j=0; j<i; ++j)
slopes.push_back(make_pair(i, j));
sort(slopes.begin(), slopes.end(), [&](pair<int, int> a, pair<int, int> b)
{
auto cs = [&](int x, int y)
{
int dx = X[x]-X[y];
int dy = Y[x]-Y[y];
if(dx<0) dx=-dx, dy=-dy;
return make_pair(dy, dx);
};
pair<int, int> ca = cs(a.first, a.second);
pair<int, int> cb = cs(b.first, b.second);
if(cb.second == 0) return false;
if(ca.second == 0) return true; // infinite slope first
return 1LL*ca.first*cb.second < 1LL*ca.second*cb.first;
});
vector<int> perm(N), invperm(N);
for(int i=0; i<N; ++i) perm[i] = i;
sort(perm.begin(), perm.end(), [&](int a, int b)
{
return make_pair(X[a], -Y[a])< make_pair(X[b], -Y[b]);
});
for(int i=0; i<N; ++i) invperm[perm[i]] = i;
long long diag = 0;
long long ans = 0;
long long minarea = (long long)8.5e18;
auto upd = [&](int a, int b, int c, int d)
{
long long x = abs(ccw(a, b, d)) + abs(ccw(c, b, d));
bool conc = (sgn(ccw(a,c,b)) == sgn(ccw(a,c,d)));
if(minarea > x)
{
minarea = x;
ans = 0;
}
if(minarea == x)
{
++ans;
if(conc) ++ans;
}
};
for(auto tmp: slopes)
{
int x, y; tie(x, y) = tmp;
int ipx = invperm[x], ipy = invperm[y];
assert(abs(ipx-ipy) == 1);
swap(perm[ipx], perm[ipy]);
swap(invperm[x], invperm[y]);
int k = min(ipx, ipy);
for(int i=max(0, k-2); i<k; ++i)
for(int j=k+2; j<min(k+4, N); ++j)
upd(perm[i], perm[k], perm[j], perm[k+1]);
diag += k * (N-k-2);
}
return diag+ans;
}
int main()
{
scanf("%d", &N);
for(int i=0; i<N; ++i) scanf("%d%d", X+i, Y+i);
printf("%lld\n", solve());
}
G
#include<bits/stdc++.h>
using namespace std;
int N;
const int MAXN = 131072;
int X[MAXN], C[MAXN];
int idx[2*MAXN];
int getv(int a, int b)
{
a+=MAXN; b+=MAXN;
int ans = 0x3f3f3f3f;
while(a<=b)
{
if(a%2==1) ans = min(ans, idx[a++]);
if(b%2==0) ans = min(ans, idx[b--]);
a/=2; b/=2;
}
return ans;
}
void setv(int a, int v)
{
idx[a+=MAXN] = v;
while((a=a/2))
idx[a] = min(idx[2*a], idx[2*a+1]);
}
int main()
{
scanf("%*d%d", &N);
for(int i=0; i<N; ++i) scanf("%d", X+i);
for(int i=0; i<N; ++i) scanf("%d", C+i);
memset(idx, 0x3f, sizeof idx);
int tp = 0;
while(C[0] == C[tp])
setv(tp++, 1);
int ptp = 0;
while(tp < N)
{
int ntp = tp;
while(C[tp] == C[ntp]) ++ntp;
int lpos = tp;
int rpos = tp-1;
for(int i=tp; i<ntp; ++i)
{
while(lpos != ptp && X[tp-1]-X[lpos-1] <= X[i]-X[tp-1]) --lpos;
while(rpos != ptp-1 && X[tp]-X[rpos] < X[i]-X[tp]) --rpos;
int ans = min(getv(lpos, rpos), getv(tp, i-1) )+1;
setv(i, ans);
}
ptp = tp, tp = ntp;
}
printf("%d\n", getv(ptp, N-1));
}
H
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2048;
long long dp[2*MAXN];
long long dpL[2*MAXN];
long long dpR[2*MAXN];
long long sumv[2*MAXN];
void setv(int a, int v)
{
a += MAXN;
sumv[a] += v;
dp[a] = dpL[a] = dpR[a] = max(0LL, sumv[a]);
while((a=a/2))
{
dp[a] = max({dp[2*a], dp[2*a+1], dpR[2*a] + dpL[2*a+1]});
dpL[a] = max(dpL[2*a], sumv[2*a] + dpL[2*a+1]);
dpR[a] = max(dpR[2*a+1], sumv[2*a+1] + dpR[2*a]);
sumv[a] = sumv[2*a] + sumv[2*a+1];
}
}
long long getv()
{
return dp[1];
}
void clear()
{
memset(dp, 0, sizeof dp);
memset(dpL, 0, sizeof dpL);
memset(dpR, 0, sizeof dpR);
memset(sumv, 0, sizeof sumv);
}
int main()
{
int N;
vector<tuple<int, int, int> > V;
vector<int> xc, yc;
int N1, N2;
cin >> N1;
for(int i=0; i<N1; ++i)
{
int x, y; cin >> x >> y;
V.emplace_back(x, y, +1);
xc.push_back(x);
yc.push_back(y);
}
cin >> N2;
for(int i=0; i<N2; ++i)
{
int x, y; cin >> x >> y;
V.emplace_back(x, y, -1);
xc.push_back(x);
yc.push_back(y);
}
N = N1+N2;
int c1, c2; cin >> c1 >> c2;
for(int i=0; i<N; ++i)
{
if(get<2>(V[i]) == 1)
get<2>(V[i]) = c1;
else
get<2>(V[i]) = -c2;
}
sort(xc.begin(), xc.end());
xc.erase(unique(xc.begin(), xc.end()), xc.end());
sort(yc.begin(), yc.end());
yc.erase(unique(yc.begin(), yc.end()), yc.end());
int K = xc.size();
vector<vector<pair<int, int> > > dat(K);
for(int i=0; i<N; ++i)
{
int x, y, w; tie(x, y, w) = V[i];
x = lower_bound(xc.begin(), xc.end(), x) - xc.begin();
y = lower_bound(yc.begin(), yc.end(), y) - yc.begin();
dat[x].emplace_back(y, w);
}
long long ans = 0;
for(int i=0; i<K; ++i)
{
clear();
for(int j=i; j<K; ++j)
{
for(auto tmp: dat[j])
{
int y, w; tie(y, w) = tmp;
setv(y, w);
}
ans = max(ans, getv());
}
}
printf("%lld\n", ans);
}
I
#include<bits/stdc++.h>
using namespace std;
int main()
{
int N;
vector<pair<int, int> > V;
cin >> N;
for(int i=0; i<N; ++i)
{
int a, b; cin >> a >> b;
V.emplace_back(a, a+b);
}
sort(V.begin(), V.end());
function<bool(int)> can = [&](int x)
{
int left_end = 0;
for(auto tmp: V)
{
int l, r; tie(l, r) = tmp;
left_end = max(left_end, l);
if(left_end > r) return false;
left_end += x;
}
return true;
};
int lo = 0;
int hi = (int)2e9+1;
while(lo+1!=hi)
{
int mi = lo + (hi-lo)/2;
if(can(mi)) lo = mi;
else hi = mi;
}
cout << lo << endl;
}
J
#include<bits/stdc++.h>
using namespace std;
int main()
{
int N; cin >> N;
for(int k=0;;++k)
{
int maxnode;
if(k%2==1)
maxnode = 4<<(k/2);
else
maxnode = 3<<(k/2);
if(N<=maxnode)
{
cout << k << endl;
return 0;
}
}
}
K
#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
using namespace std;
using P = tuple<long long, long long, long long>;
vector<P> coord;
int N, K;
P operator -(P a, P b)
{
long long ax, ay, az; tie(ax, ay, az) = a;
long long bx, by, bz; tie(bx, by, bz) = b;
return P(ax-bx, ay-by, az-bz);
}
P operator *(P a, P b)
{
long long ax, ay, az; tie(ax, ay, az) = a;
long long bx, by, bz; tie(bx, by, bz) = b;
long long cx = ay*bz-az*by;
long long cy = az*bx-ax*bz;
long long cz = ax*by-ay*bx;
return P(cx, cy, cz);
}
long long operator ^(P a, P b)
{
long long ax, ay, az; tie(ax, ay, az) = a;
long long bx, by, bz; tie(bx, by, bz) = b;
return ax*bx+ay*by+az*bz;
}
double var(const vector<P>& V)
{
long long exr = 0, exg = 0, exb = 0, ex2 = 0;
for(int i=0; i<(int)V.size(); ++i)
{
long long r, g, b; tie(r, g, b) = V[i];
exr += r; exg += g; exb += b;
ex2 += r*r+g*g+b*b;
}
return ex2-(exr*exr+exg*exg+exb*exb)/(double)V.size();
}
double tryfor(int x, int y, int z)
{
P Plane = (coord[y]-coord[x])*(coord[z]-coord[x]);
vector<P> p1, p2;
for(int i=0; i<N; ++i)
{
if(i==x||i==y||i==z) continue;
if( ((Plane)^(coord[i]-coord[x])) > 0 ) p1.push_back(coord[i]);
else p2.push_back(coord[i]);
}
double ans = 1e18;
for(int xp=0; xp<2; ++xp)
{
for(int yp=0; yp<2; ++yp)
{
for(int zp=0; zp<2; ++zp)
{
if(xp==yp&&yp==zp) continue;
if(xp) p1.push_back(coord[x]); else p2.push_back(coord[x]);
if(yp) p1.push_back(coord[y]); else p2.push_back(coord[y]);
if(zp) p1.push_back(coord[z]); else p2.push_back(coord[z]);
ans = min(ans, var(p1)+var(p2));
if(xp) p1.pop_back(); else p2.pop_back();
if(yp) p1.pop_back(); else p2.pop_back();
if(zp) p1.pop_back(); else p2.pop_back();
}
}
}
return ans;
}
double solve()
{
if(N<=K) return 0;
if(K == 1) return var(coord);
double ans = 1e18;
for(int i=0; i<N; ++i)
for(int j=0; j<i; ++j)
for(int k=0; k<j; ++k)
ans = min(ans, tryfor(i, j, k));
return ans;
}
int main()
{
scanf("%d%d", &N, &K);
for(int i=0; i<N; ++i)
{
int r, g, b; scanf("%d%d%d", &r, &g, &b);
coord.emplace_back(r, g, b);
}
printf("%.6lf\n", solve());
}
L
#include<bits/stdc++.h>
using namespace std;
int M, N;
int A[10101];
vector<pair<int, int> > SC[15101];
int D[15101];
int main()
{
cin >> M >> N;
for(int i=0; i<M; ++i) cin >> A[i];
for(int i=0; i<N; ++i)
{
int s, e, t;
cin >> s >> e >> t;
int cost = (e-s)*A[t-1];
SC[e].emplace_back(s, cost);
}
for(int i=1; i<15101; ++i)
{
D[i] = D[i-1];
for(auto tmp: SC[i])
{
int s, t; tie(s, t) = tmp;
D[i] = max(D[s]+t, D[i]);
}
}
cout << D[15001] << endl;
}