Tree Isomorphism
소개
안녕하세요. 이번 글에서는 Tree Isomorphism에 대해 소개해드리려고 합니다. Isomorphism이란 어떤 두 대상이 수학적으로 동등한 관계에 있음을 나타내는 용어인데, 트리에서의 Isomorphism이라 하면 한쪽 트리의 정점을 적절히 renumbering했을 때 다른 한 쪽 트리와 같아지는 것을 말합니다. (정확히는 그러한 mapping을 가리킵니다.)
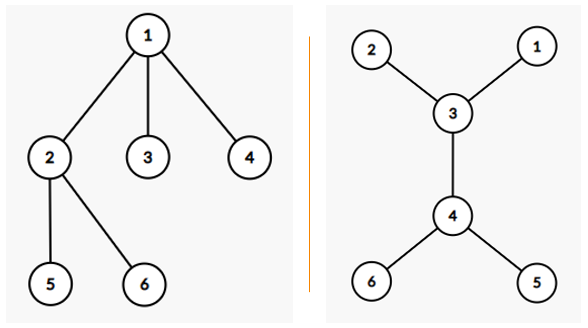
이해를 돕기 위해, 다음과 같이 두 개의 트리가 있다고 합시다.
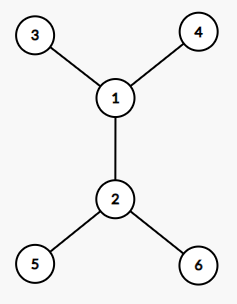
딱 보면 두 트리의 모양이 달라보이지만, 오른쪽 트리의 정점을 아래와 같이 renumbering하면 왼쪽 트리와 완전히 같은 연결 관계를 갖게 됩니다. 즉, 두 트리는 isomorphic합니다.
이처럼 두 트리가 주어졌을 때 isomorphic한지 판단하는 방법에 대해 알아보겠습니다.
Rooted Tree Isomorphism
우선 문제를 조금 쉽게 하기 위해 일반적인 트리가 아닌 rooted tree에 대한 isomorphism 여부를 판단한다고 가정하겠습니다. (아래에서 다시 언급하겠지만, rooted가 아닌 경우에도 rooted로 바꿔 생각할 수 있습니다.) 그리고 두 트리를 각각 $T_1$, $T_2$라고 합시다.
만약 $T_1$, $T_2$의 루트가 자식을 갖지 않는, 즉 단일 정점의 트리라면 isomorphic함이 자명합니다.
그러면 $T_1$, $T_2$의 루트가 자식을 갖고 있는 경우를 생각해봅시다. 당연히 자식의 수는 서로 같아야 합니다. 또한, 각 자식을 루트로 하는 서브트리들도 서로 isomorphic해야 한다는 것을 알 수 있습니다. 그러나 문제는, $T_1$의 어떤 서브트리가 $T_2$의 어떤 서브트리와 매칭되어야 하는지 알 수가 없습니다.
이런 아이디어를 생각해봅시다. 만약 서브트리를 나타내는 어떤 unique한 표현 방법이 존재한다면(숫자나 문자열 등..), $T_1$과 $T_2$ 각각의 서브트리들을 표현값에 대해 (오름차순) 정렬하여 같은 index에 있는 서브트리들끼리 비교하면 됩니다. 그리고 이 표현값들을 잘 조합하면 전체 트리에 대한 표현값도 나타낼 수 있을 것입니다. 이러한 재귀적인 관계로부터, 임의의 rooted tree에 대한 isomorphic tuple을 다음과 같이 정의할 수 있습니다.
$R(T)$ : Rooted tree $T$의 isomorphic tuple
i) $T$가 하나의 정점으로 이루어진 경우 : $R(T) = (0)$
ii) $T$가 두 개 이상의 정점으로 이루어진 경우 : 서브트리들을 $S_1, S_2, …, S_k$라고 하면 $R(T) = (R(S_1), R(S_2), …, R(S_k))$ (단, $R(S_1)\leq R(S_2)\leq …\leq R(S_k)$)
임의의 두 트리가 isomorphic할 필요충분조건은 $R(T_1)=R(T_2)$입니다. 정의 자체가 직관적이기 때문에 자세한 증명은 생략하겠습니다. (수학적 귀납법으로 보일 수 있습니다.)
시간복잡도
우선 $R$의 길이는 트리에 포함된 정점의 수 $n$에 비례함을 알 수 있습니다. 만약 어떤 정점 $u$의 자식 수가 $k$고, 각 자식의 서브트리에 포함된 정점의 개수가 $s_i (1\leq i\leq k)$ 면 정렬하는 데 드는 시간은 $O(kmax(s_i))$ 입니다. (radix sort 등을 사용할 경우) 여기서 $k$는 해당 정점의 degree에 비례하고 $max(s_i)$는 서브트리의 정점 수에 비례하기 때문에 $O(n^2)$이라고 생각할 수도 있습니다. 그러나 $k$들의 합이 $n$을 넘지 않기 때문에 트리 전체적으로 보았을 때에는 amortized $O(n)$이 됩니다. 즉, $n$개의 정점마다 $n$에 비례한 연산을 필요로 하기 때문에 총 시간복잡도는 $O(n^2)$입니다.
개선
좀 더 빠르게 할 수는 없을까요? 사실 우리가 원하는 것은 튜플 값 자체가 아니라 두 트리의 튜플 값이 같은지 다른지 판단하는 것 뿐입니다.
튜플이 만들어지는 과정을 생각해봅시다. 리프에서는 길이가 1이었던 튜플이 위로 올라갈수록 비대해집니다. 그러면 애초에 튜플을 다 만들고 나서 비교할 것이 아니라, 아래에서부터 튜플을 비교할 수는 없을까요?
좀 더 구체적인 방법을 설명하기에 앞서 알아두어야 할 것이 있습니다.
Lemma 1. $T_1$과 $T_2$가 isomorphic할 필요충분조건은 임의의 $depth$에 해당하는 두 튜플 리스트가 같아야 한다.
직관적으로 생각해보면 당연한 사실입니다. 이에 따르면 $depth = max(T_1$의 높이$, T_2$의 높이$)$ 부터 $depth = 0$까지 올라오면서 튜플 리스트를 관리하고, 두 리스트가 같은지 확인하는 방법을 생각해볼 수 있습니다. 만약 중간에 리스트가 달라지는 지점이 발생하면 바로 isomorphic하지 않다는 결론을 내릴 수 있습니다.
예를 들어 $depth = k$에서 $T_1$의 튜플 리스트를 $a_1, a_2, …, a_{m_1}$, $T_2$의 튜플 리스트를 $b_1, b_2, …, b_{m_2}$이라고 합시다. ($a_i\leq a_{i+1}, b_i\leq b_{i+1}$) 만약 $m_1\neq m_2$이거나, $a_i\neq b_i$인 $i$가 하나라도 존재한다면 $T_1$과 $T_2$는 isomorphic하지 않기 때문에 알고리즘을 종료합니다. 그렇지 않다면, $a_i$와 $b_i$들을 부모 노드의 튜플로 전파시킨 후 $depth=k-1$의 튜플들을 정렬합니다. 그리고 다시 $depth=k-1$의 두 리스트를 비교하고, …$depth=0$일 때까지 반복합니다.
여기서 한 가지 중요한 최적화를 할 수 있습니다. 만약 두 튜플 리스트가 같은 것으로 판단되었을 경우, 어차피 $a_i=b_i$이기 때문에 튜플인 $a_i$ 대신 다른 어떤 값을 부모에게 넘겨주어도 됩니다. 서로 다른 두 튜플을 구별하는 것이 중요할 뿐, 구별할 수만 있다면 다른 어떤 것으로 대체해도 상관없다는 것입니다. 따라서 $a_i=a_{i+1}$인 부분만 잘 처리하여 모든 $a_i$들을 renumbering한 후 부모에게는 renumbered index만 넘겨주어도 됩니다. 그러면 중간 과정에 등장하는 모든 튜플의 길이가 해당 정점의 degree에 비례하게 됩니다.
$depth=k$에서 정점 수가 $n_k$, 최대 degree가 $d_k$라고 하면 정렬하는데 필요한 시간은 $O(n_kd_k)$입니다. 언뜻 보면 최악의 경우 $O(n^2)$일 것 같지만, 튜플들을 길이가 같은 것끼리 묶어 따로 $O(n_kd_k)$에 정렬한 후 $O(n_k)$에 합치게 하면 $n_kd_k$가 $n$을 넘을 수 없습니다. 또한 $n_k$, $d_k$ 각각의 합이 $O(n)$이므로, 총 시간복잡도는 $O(n)$이 됩니다.
사실 $O(n)$ sort의 구현이 번거롭기 때문에, C++로 구현할 경우 $O(nlogn)$인 STL sort를 사용해도 문제를 푸는 데에는 크게 지장이 없습니다(적어도 아래 소개할 문제에서는). 대신 총 시간복잡도가 $O(nlogn)$이 됩니다.
일반적인 트리의 Isomorphism
위에서는 rooted tree의 isomorphism을 살펴보았습니다. 그러면 루트가 특정되지 않은, 일반적인 두 트리의 isomorphism 여부는 어떻게 판단할 수 있을까요?
임의의 트리에 대해 항상 유일하게, 혹은 두 개 존재하는 정점이 있습니다. 바로 트리의 중심입니다. 두 트리가 isomorphic하다면, 트리의 중심을 root로 했을 때에도 isomorphic 해야할 것입니다. (만약 중심이 두 개라면 새로운 정점을 연결하여 중심을 하나로 만듭니다.) 트리의 중심은 DFS로 $O(n)$에 찾을 수 있고, rooted tree isomorphism 여부도 $O(n)$에 판단할 수 있으므로 일반적인 트리의 isomorphism 여부도 $O(n)$에 판단할 수 있습니다.
문제 1 - Automorphisms (boj.kr/8282)
Automorphism은 자기 자신과 isomorphic해지는 renumbering을 말합니다. 즉, 트리가 하나 주어지면 $n!$개의 가능한 모든 renumbering들 중 automorphism인 것의 개수를 세는 문제입니다.
한 가지 확실한 것은, 임의의 automorphism에서 트리의 중심은 항상 고정되어 있다는 것입니다. (중심이 두 개라면 새로운 정점을 추가하여 중심을 하나로 만듭니다.) 따라서 중심을 root로 잡고 위에서 설명한 것처럼 $depth=$(트리의 높이) 에서 시작하여 $depth=0$까지 올라가면서 isomorphic tuple들을 계산합니다. 이 과정에서 각 정점에 연결된 자식들을 같은 tuple끼리 묶어 그 개수만큼의 순열값($x$개면 $x!$)을 결과값에 곱해줍니다. 즉, tuple이 같은 서브트리끼리는 서로 위치 교환이 가능하다는 것입니다. 이렇게 루트까지 올라오면서 곱하는 과정을 반복하면 최종 결과를 구할 수 있습니다.
문제 2 - 거울대칭트리 그래프 (boj.kr/2430)
주어진 그래프가 거울대칭트리 그래프인지 판단하는 문제입니다.
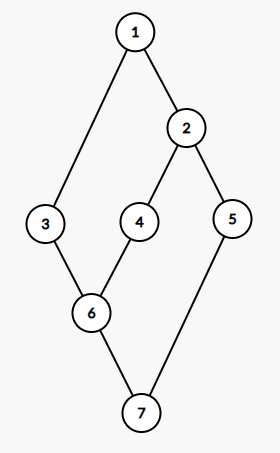
우선 각 루트와 리프 정점을 알고 있다고 가정합시다. 그러면 두 트리가 isomorphic한지 판단하면 될 것 같습니다. 그런데 주의할 점은, 리프들이 서로 구별되어야 한다는 것입니다. 리프를 구별하지 않으면 아래 그래프를 거울대칭트리라고 잘못 판단하는 참사..문제가 발생합니다.
이 문제를 해결하는 방법은 간단합니다. 앞서 단일 정점 트리(리프)의 isomorphic tuple은 (0)으로 정의했었는데, 0 대신 구별할 수 있는 값(ex. 정점 번호)을 대입하기만 하면 됩니다. 나머지 과정은 위에서 언급한 것과 같습니다.
그러면, 루트와 리프는 어떻게 찾을 수 있을까요? 여러 가지 방법이 가능하겠지만, 가장 쉬운 방법은 경우를 나누어 생각하는 것입니다.
예를 들어 그래프에 사이클이 한 개 포함된 경우, 두 개 이상 포함된 경우, … 등으로 나누어 각 경우에 대해 리프의 위치를 어떻게 구하는지 조금 생각해보면 어렵지 않게 알 수 있습니다. 조금 노가다성이 있고 글의 주제와는 크게 관련이 없어 자세한 과정은 생략하겠습니다.