Data Forecast

What is Data Forecast?
Basic Concepts
what is STL Decomposition?
Data Forecast methods
conclusion

What is Data Forecast?

Data Forecast 란 무엇인가?
데이터 예측은 많은 경우에 필요하고 그 중요성 또한 크다고 할 수 있다.
만약 돌에 걸려 넘어지게 되었을 때, 그 결과를 예측해보면 쉽게 ‘다칠 것이다’라고 말할 수 있다.
하지만 자율주행 자동차를 제작한다고 생각해보자
자동차가 빠른속도로 다가오는 트럭을 상대로 미래를 예측해야 하는 상황이 생길 것이다.
관측 가능한 모든 데이터를 고려해보자
자동차의 현재 속도, 가속도, 질량, 땅바닥의 마찰, 저항, 트럭의 속도, 가속도, 질량 그리고 트럭과 자동차의 거리 등 나열한 것보다,
수십, 수만가지의 데이터를 고려해 속도를 줄이거나 방향을 변경하는 등, 조치를 취해주어야 하는 상황이 존재한다.
이런 작업이 사람또한 완벽하게 가능하지 않아서 안타까운 사고가 종종 일어나고는 한다.
이런 경우 외에도, 많은 사람들이 주식변동을 예측하기 위해 매일같이 노력하고 있고,
매일 아침,저녁 알려주는 기상예보에서도 날씨를 예측하고 있으며, 여러 업체에서는 고객들의 수요량을 예측하기 위해 노력하고 있다.

이렇게 우리 주변에는 많은 종류의 예측들이 존재하고 그 중요성 또한 매우 높다고 할 수 있다.
데이터 예측을 잘하면 할 수록, 한 발 앞선 생각을 할 수 있고, 상대적으로 더 큰 이득을 올릴 수 있기 때문이다.

그렇다면 이런 데이터 예측중에서도 시계열 데이터 분석을 실제로 어떻게 진행하는지 살펴보도록 하자.

Basic Concepts

먼저 Data Forecast에 들어가기에 앞서서 기본적인 순서와 개념들을 짚고 넘어갈 필요성이 있다.

우선 우리는 예측의 목표를 세워야 한다. 예측을 하고자 하는 주체가 누구이고, 목표가 무엇인지를 확실히 할 필요가 있다.
이 목표에 따라서 방법 또는 그 난이도가 매우 달라질 수 있기 때문이다.
그 후에 우리는 예측의 기본이 되는 데이터들을 모아야 한다.
이는 웹 크롤링을 통해 이루어질 수도 있고, 실제 직접 발로 뛰어(사진을 찍거나, 수치를 측정한다는 뜻) 수집할 수도 있다.
또한 데이터에 대한 전문 지식을 통한 판단 또한 예측의 기반이 되는 데이터라고 할 수 있다.
데이터 분석이 필요하다.
앞서 우리는 데이터를 읽어오고, 잘 이해할 수 있는 방법들을 살펴보았다. 그 과정이 이 곳에 해당한다고 볼 수 있다.
예측
우리가 앞서 해본 여러가지 모델들이 있다.
linear regression(선형 회귀), 신경망(neural network), ETS model, ARIMA model 등 이 중에서
데이터에 따라 어떤 모델이 좋은 모델이 될지가 결정되게 된다. 이를 잘 결정하고 예측을 수행해 주어야 한다.
그렇다면 이제 실제 시계열 데이터 예측에서 사용되는 기본적인 단어 개념들을 짚어보겠다.

시계열(time series) : 말 그대로 일정 시간 간격으로 이루어진 시간이 x값, data가 y값을 이루는 데이터 sequence라고 생각하면 된다.
frequency(빈도수) : 위에서 얘기한 기준이 되는 시간 간격이다. 일반 data에도 frequency를 추가한다면 시계열데이터가 될 수 있다.
trend(추세) : 데이터가 장기적인 측면에서, 증가하거나 감소하는 모양세를 말한다.
계절성(seasonality) : 데이터에서 해마다 또는 특정 달마다 나타나는 특정 변동을 뜻한다.
산점도(scatter plot) : 두 시계열 사이의 관계를 살펴볼 때 유용한 그래프
상관(correlation) : 산점도는 단순히 관계를 그려낸 것이라면, 상관은 그 강도를 수학적으로 수치이다.
자기상관(autocorrelation) : 어떤 시계열의 시차 값 사이의 상관(관계의 강도)을 나타낸다

이런 기본적인 단어들을 바탕으로 시계열 성분이라는 개념에 다다르게 된다.
시계열 값 Y(t) 는 위에서 설명한 추세 T(t) 와, 계절성 Y(t) 그리고 나머지 R(t)로 표현할 수 있다.
이렇게 시계열 데이터를 분해하는 방법은 여러가지가 존재한다.
단순한 계산과 이동편균을 이용해서 계산하는 방법과, X11분해, SEATS분해(ARIMA 모델에서 사용), STL분해 등이 존재한다. 우리는 STL분해가 실제로 어떻게 구현이 되는지 자세히 짚고 넘어가 볼 것이다.

What is STL Decomposition?

STL Decomposition (STL 분해)

기존 데이터 Y(t)에 대해
STL(seasonal trending decomposition using Loess) 분해는
Seasonal, Trending, Remain 3값으로 분해하는 것을 의미한다.

즉 Y(t) = S(t) + T(t) + R(t) (t in time)
STL 분해는 Loess smoothing을 통해 이루어진다. loess라는 단어는 Local Regression의 약자로
local regression은 어떤 점을 기준으로 근방(locally)하게 회귀를 진행하는 것이다.

아래 설명에 Low-pass filter 라는 단어가 나오게 되는데 이는 저역통과 필터라는 뜻으로,
특정 차단주파수 아래인 저역주파수 성분만을 통과시킬 수 있게 하는 필터를 의미한다.

실제 알고리즘의 진행 방식을 살펴볼건데, 2개의 반복문을 통해 이루어진다.
outer loop 와 inner loop 두개로 나뉠수 있는데
간단하게 표현하면, inner loop에서는

Detrending ->
Cycle-subseries Smoothing ->
Low-pass Filtering of Smoothed Cycle-subseries ->
Detrending of Smoothed Cycle-subseries ->
Deseasonalizing ->
Trend Smoothing

으로 이루어진다.

outer loop 에서는 초기 inner loop에서 구해진 예측된 T,S 를 이용해서 R, weights 를 구하게 된다.
R = Y - S - T 로 표현이 가능하다. Y에 대해 각 time 별로 weights들을 정의할 것이다.
h = 6 * median(|R|) 이라 두고,
w = B(|R| / h) 와 같이 weight를 계산하게 된다.
이때 B()는 Bi-square function으로 아래와 같다.
B(n) = (1 - n^2)^2 for 0 <= n <= 1
B(n) = 0 for else

이제 다시 inner loop가 반복되게 되며, 초기 inner loop와 다르게
step 2,6 smoothing 에서 neighborhood weight가 앞서 구한 w로 곱해지게 된다.

inner loop의 진행 방식을 자세히 살펴보면 n(i) 번 돌리게 되며,

Detrending 데이터에서 trend(추세) 부분을 제거하는 작업이다. 즉 Y - T 를 계산하는 작업이다.
Cycle-subseries Smoothing 각 추세가 제거된 series는 cycle-subseries 로 분해되게 된다.
(그 예로, 12개월의 주기를 가진 data의 경우에, 12개의 cycle-subseries로 분해가 되며, 그 중 하나는 모든 1월을 포함한 data가 된다)
(위의 예에서는 n(p) = 12 가 된다)
그 후, 각 cycle-subseries들을 q = n(s), d = 1 값으로 loess를 이용해 평활화를 진행한다
이 때 missing value 들도 모두 값을 매기게 된다. 이 평활화된 값들은 일시적인 계절 시계열 Ck+1을 산출하게 된다.
Low-pass Filtering of Smoothed Cycle-Subseries Ck+1에 Low-pass filter를 입히면 Lk+1을 산출하게 된다. 필터는 길이 n(p)의 이동평균, 길이 n(p)의 또다른 이동평균,
길이 3의 이동평균, 마지막으로 q = n(l), d = 1 값으로 loess를 이용한 평활화값로 구성되게 된다.
n(l)의 경우 주기보다 큰 가장 작은 홀수 정수로 default값이다. (위의 예처럼 monthly data인 경우 13)
Detrending of Smoothed Cycle-subseries S(k+1) = C(k+1) - L(k+1) 을 진행한다. (v = 1 to N)
이는 seasonal 요소의 k+1번째 추정치가 된다. low-pass filter는 이 시계열의 평균을 0이 되게 만든다.
Deseasonalizing Y - S(k+1) 을 진행한다. 만약 time v에서 Y값이 missing 이라면, deseasonalized series에서도 missing 이 된다.
Trend Smoothing 계절 요소가 제거된 data를 q = n(t), d = 1 값으로 loess를 이용해 평활화 하는 부분이다.
이 결과 값은 T(k+1) (v = 1 to N) 이 되고 이는 추세 요소의 (k+1)번째 추정치가 되게 된다.

위에서 사용된 parameter들을 간단히 정리하자면 아래와 같다.
n(p) = 계절(seasonal) 요소 의 주기값이다.
n(i) = i : inner 을 의미하며, inner loop를 돌리는 횟수이다. 이는 수렴에 도달하기 위한 적절한 수이면 가능한데,
전형적으로 2 또는 3의 값을 가진다고 한다.
n(o) = o : outer 을 의미하며, outer loop를 돌리는 횟수이다. 여러번 돌릴 수록 data에서 outlier(이상치)들의 영향이 적어지는 효과가 있다.
대부분의 경우 0(outlier가 없는 경우) 아니면 1의 값을 가진다.

n(l) = l : low-pass filter 를 의미하며, 저역통과의 지연 기간을 나타내며, 평활화 parameter로 사용된다.
이 때, n(p)값보다 큰 수 중 가장 작은 홀수 값을 대부분 가지게 된다.
n(s) = s : seasonal 을 의미하며, 계절 요소의 평활화 parameter값이다. 이 때, n(s) 값이 증가할수록,
각 cycle-subseries들은 더욱 평활화되게 된다. n(s) 값은 고정되어 있지 않고, 우리가 분해하고자 하는 data에 맞게 잘 조정해주어야 한다.
n(t) = t : trend 를 의미하며, 추세 요소의 평활화 parameter값이다. 역시 증가할수록, trend 요소가 평활화된다.

즉 우리가 직접적으로 항상 수정해주어야 하는 값은 n(p), n(s)라고 할 수 있다.

n(p)는 내가 확인하고 싶은 데이터의 주기에 맞게 설정해주면 되고,
n(s)의 경우에는 seasonal 요소의 평활화 정도를 관리한다고 앞에서 설명하였다.
따라서 내가 얼마나 계절 요소 변화에 의미를 두고 싶은지에 따라 그래프를 plot 해보며 적당한 값을 적용시켜 주면 된다.

그럼 실제 데이터에 대해서 stl decomposition을 수행해보겠다.
모든 소스코드는 R을 기반으로 작성했다.

library(xts)
library(dygraphs)
library(extrafont)
library(lubridate)
library(httr)
library(rvest)
code = "005930"
url = paste0("https://fchart.stock.naver.com/sise.nhn?symbol=",code,"&timeframe=day&count=1000&requestType=0")
samsung = GET(url) %>%
  read_html %>%
  html_nodes("item") %>%
  html_attr("data") %>%
  strsplit("\\|")

samsung = lapply(samsung, function(x){ # list로 이루어진 data를 1,5 행을 골라내, dataframe으로 만들어준다.
  x[c(1, 5)] %>% t() %>% data.frame()
})

samsung = do.call(rbind, samsung) # 만들어진 dataframe을 행별로 하나루 묶어준다.

samsung[,2] = as.numeric(as.character(samsung[,2])) # 문자열을 숫자로 바꿔준다.(종가부분)
rownames(samsung) = ymd(samsung[,1]) %>% as.character # 날짜data문자열을 날짜값으로 바꿔준다.(R에서 인식을 하기위해)
samsung[,1] = NULL
# plot(samsung)

ho <- ts(samsung[[1]], frequency = 12) 시계열 분해를 위해, frequency를 준다.
ho %>%
 stl(t.window=13, s.window="periodic", robust=TRUE) %>%  # 위에서 설명한 n(t), n(s) parameter값들을 지정해준다.
 autoplot()

아래는 위 코드의 실행 결과 그래프이다.
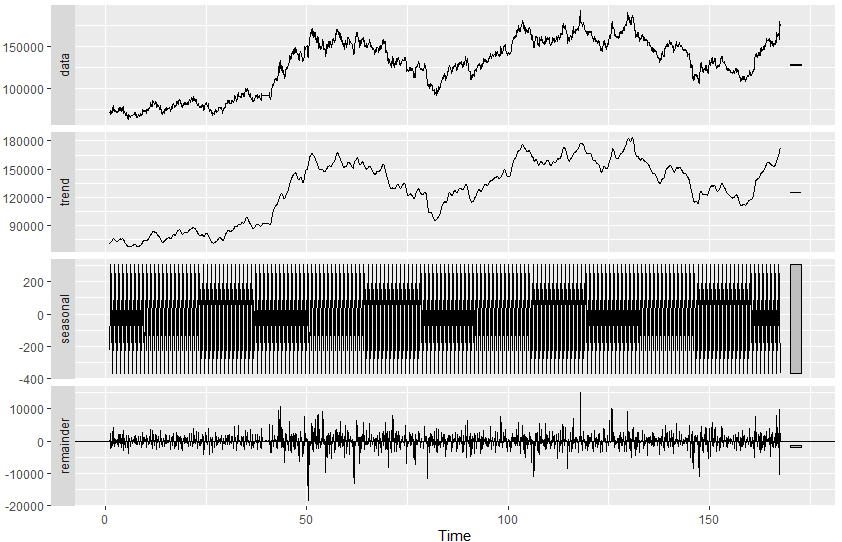
STLsamsung

trend 요소도 잘 평활화 되지 않았고, (사실상 원 data와 거의 비슷하다)
계절 요소도 별반 뚜렷한 특징이 없는 것을 확인할 수 있다.
이는 데이터의 특성에서 살펴볼 수 있는데, 모든 data에서 STL분해가 우리에게 원하는 결과를 주는 것이 아니다.

우리가 가져온 삼성전자의 주식 종가 정보에는 뚜렷한 추세나, 계절별 특성이 없다는 것을 의미하고 있는 것이다.
따라서 만약 우리가 주식 종가를 예측한다고 했을 때, 시계열 데이터에 사용되는 예측 모델을 사용한다면 쫄딱 망하게 되는 것이다.

그렇다면 fpp library package에 내장되어 있는 시계열 분석이 아주 뜻깊은 데이터들을 이용해 살펴보자.
내가 사용해본 데이터는 1992년 ~ 2008년까지 호주에서 월간 항 당뇨병 약의 판매량을 나타넨 데이터이다.

library(fpp)
data(a10)
plot(a10)

a10_ts <- ts(a10, frequency = 12)
plot(a10)

trend_a10 <- ma(a10, order = 12, centre = T)
plot(a10)
lines(trend_a10)

detrend_a10 <- a10 - trend_a10
plot(detrend_a10)

결과는 아래와 같다.
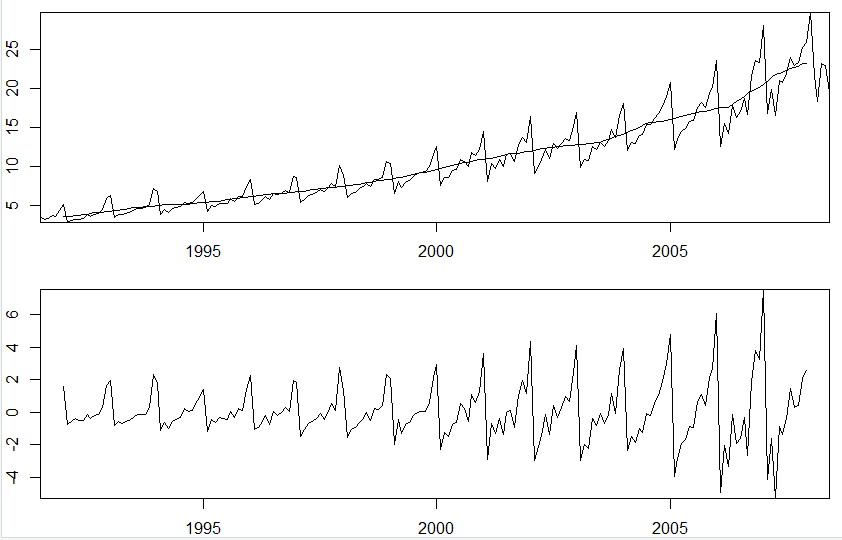
trend

trend 요소가 뚜렷하게 걸러졌고, 추세요소를 제거한 Y-T 값도 잘 나오는 모습이다.
계절성 요소도 확인해 보자.

m_a10 <- t(matrix(data = detrend_a10, nrow = 12))
seasonal_a10 <- colMeans(m_a10, na.rm = T)
seasonal_a10 <- ts(rep(seasonal_a10,17), start=1992, frequency=12)
plot(seasonal_a10)

seasonal_a10 <- colMeans(m_a10, na.rm = T)
remain_a10 <- a10 - trend_a10 - seasonal_a10
plot(remain_a10)

a10 %>%
  stl(t.window=13, s.window="periodic", robust=TRUE) %>%
  autoplot()

결과는 아래와 같다.
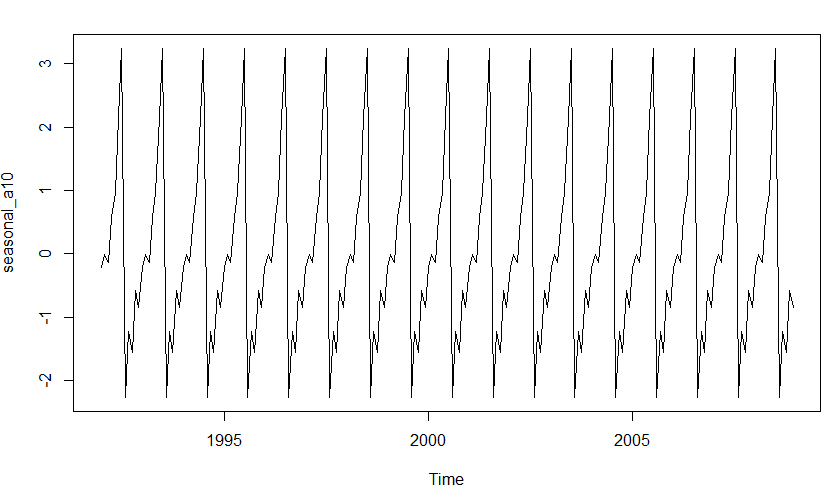
seasonal

seasonal 요소가 뚜렷하게 걸러졌다.
마지막에 stl 함수를 이용해 분해된 그래프와 비교해보자.
stl2

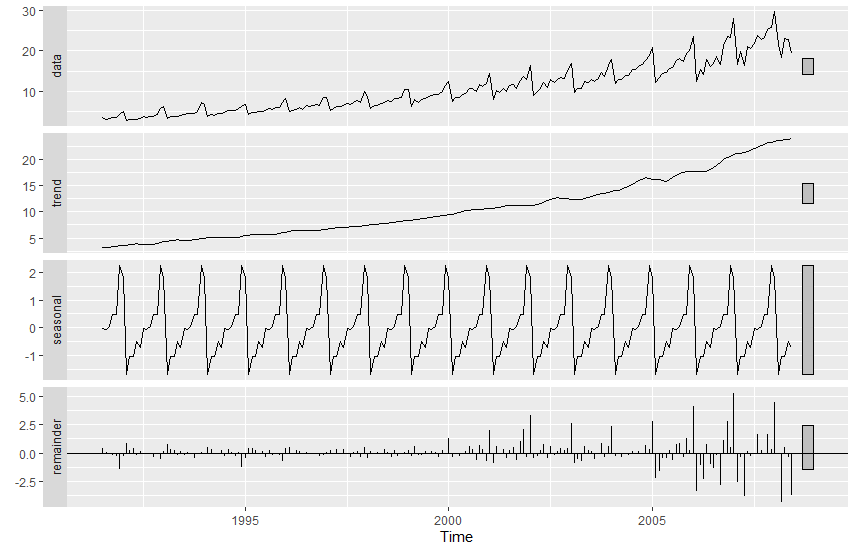
올바르게 분해 된 것을 확인할 수 있다.

Data Forecast Method

ETS모델을 적용시키는 것만 저번에 다루었었다.
이제는 여러가지 시계열 데이터를 예측하는 방법인 지수평활법에 대해 알아보자.
단순 지수 평활법과, 이중 지수 평활법이 있는데,
단순 지수 평활법은 현재 값 y(t-1)와, 이전 예측치 s(t-1)에다가 각각 가중치를 곱해서 더한 값으로 s(t)를 계산한다.
즉 s(t) = alpha * y(t-1) + (1 - alpha) * s(t-1) 이 되는 것이다. 이를 python code로 작성해보았다.
사용된 데이터는 백화점 매출 데이터이다.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

data = pd.read_csv("data.csv", thousands = ",")

data = data[0:298]

si = len(data.index)
x = np.arange(len(data.index))
y = data["Value"]

plt.figure()
plt.title("alpha = 0.1 ES")
plt.plot(x,y)

alpha = 0.1
S = np.zeros(si + 50)
x = np.arange(0, si + 50)
y = np.zeros(si + 50)
for i in range(si + 50):
    if i >= si :
        y[i] = data["Value"][si - 1]
    else:
        y[i] = data["Value"][i]
S[0] = y[0]
for i in range(si + 50):
    if i > 0:
        S[i] = (1 - alpha) * S[i-1] + alpha * y[i-1]
plt.plot(x,S)

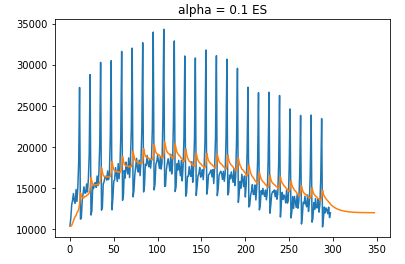보다시피 원본 데이터를 잘 따라가고 있지만, 추세에 약한 모습을 보인다.
따라서 이중 지수 평활법이라는 것이 나왔는데, 이는 추세 변화량을 보정(평활화)하여 기존 지수 평활법에 더해주는 방법이다.
식으로 표현하면 다음과 같다
s(t) = alpha * y(t) + (1 - alpha) * (s(t-1) + b(t-1))
b(t) = gamma * (s(t) - s(t-1)) + (1 - gamma) * b(t-1)
F(t+m) = s(t) + m * b(t)

이를 구현한 코드이다.

plt.figure()
plt.title("alpha = 0.9, gamma = 1.0 double ES")
plt.plot(x,y)
alpha = 0.9
gamma = 1.0
S = np.zeros(si + 50)
B = np.zeros(si + 50)
x = np.arange(0, si + 50)
for i in range(si + 50):
    if i >= si :
        y[i] = data["Value"][si - 1]
    else:
        y[i] = data["Value"][i]
S[0] = y[0]
for i in range(si + 50):
    if i > 0:
        S[i] = (1 - alpha) * (S[i-1] + B[i-1]) + alpha * y[i-1]
        B[i] = (1 - alpha) * B[i-1] + gamma * (S[i] - S[i-1])
plt.plot(x,S)

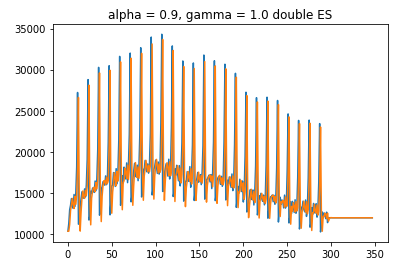ees 거의 완벽에 가깝게 예측이 진했되었는데, 이는 내가 구해온 데이터가 너무 깔끔한 형태를 가지고 있어서 그런 모습이다.
이제 우리는 마지막인 ETS 모델에 다르게 되었는데, ETS모델은
세개의 요소인 Error, Trend, Seasonal 3가지 요소로 구성된 모델을 의미한다.

그렇다. 앞서 stl decomposition에서 구해낸 3가지 요소가 사용된다.
R에서는 매우 간단하게 앞서 다룬 a10데이터 코드에

a10 %>% forecast(h=20) %>%
  autoplot() 를 추가하면 ETS 모델로 예측을 진행해준다. h 값은 예측 할 기간이다.<br> 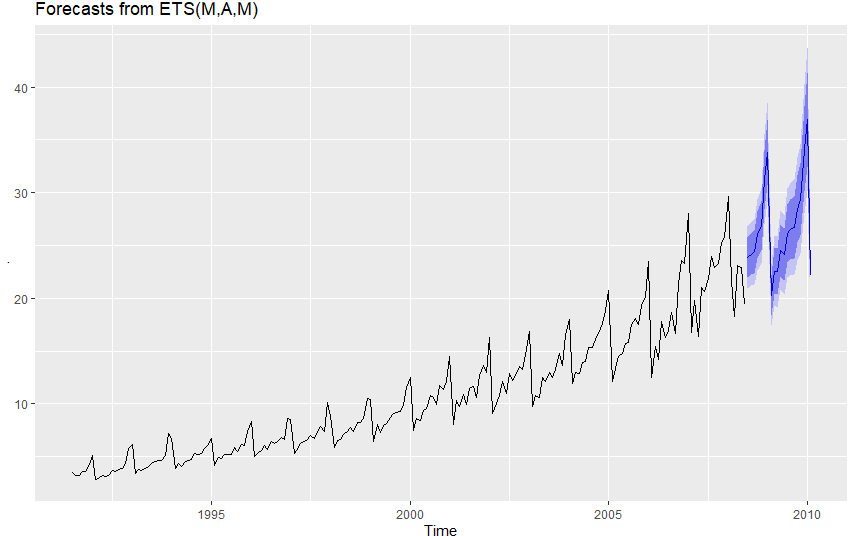![ets](/assets/images/dataForecast/07.png)

Conclusion

우리는 이번에 ETS 모델에 기본이 되고, 시계열 데이터를 분석하는데에 있어서 기본이되는,
STL Decomposition에 대해 자세히 알아봤다. ETS모델이 데이터의 추세,계절성에 관심을 두었다면,
데이터에 나타나는 자기상관(autocorrelation)을 이용하는 ARIMA모델도 존재한다.

주어진 데이터에 대하여, 어떤 모델을 사용하여 예측을 할지를 정하는 것이 좋은 예측 결과값을 산출하게 된다.
추세가 있고 계절성이 나타나는 데이터에는 ETS모델을, 잡음이 크지만 추세가 강한경우 회귀를 사용할 수 있다.
기후 예측 또는 human motion 예측 같은 데이터에는 복잡한 신경망을 사용하게 된다.

이렇게 데이터 예측 분야는 데이터 분석에 있어서 가장 실용적이고 큰 범주를 다루고 있다.
앞으로도 만약 새롭게 알게된 데이터 분석방법 또는 데이터 예측방법이 있다면 꼭 다뤄보도록 하겠다.

Reference

STL: a seasonal-trend decomposition procedure based on Loess (with discussion) by (Cleveland, RB Cleveland, WS McRae, JE Terpenning, I.)

http://www.gardner.fyi/blog/STL-Part-II/

Data Forecast

Data Forecast

contents

What is Data Forecast?

Basic Concepts

What is STL Decomposition?

Data Forecast Method

Conclusion

Reference

On Factoring Given Any Bits

Exchange argument