Deep Q-learning으로 뱀 게임 인공지능 만들기
machine-learning , reinforcement-learning , deep-Q-learning , Keras
소개
강화학습 알고리즘을 테스트하기 위해 다양한 라이브러리를 사용할 수 있지만 원하는 환경이 없는 경우가 종종 있습니다. 이런 경우 간단한 환경은 pygame, opencv 같은 라이브러리를 가지고 직접 만들어서 테스트해볼 수 있습니다.
이번 포스트에서는 뱀 게임 환경을 직접 구현하고 강화학습 알고리즘을 적용하는 과정을 살펴볼 것입니다. 이를 위해 pygame으로 뱀 게임을 만들고 Keras로 딥마인드의 “Playing Atari with Deep Reinforcement Learning”에서 소개되었던 DQN(Deep Q-Networks)을 구현 해보겠습니다. 본 포스트에서 다루는 뱀 게임 인공지능 전체 코드는 여기에서 확인할 수 있습니다.
DQN으로 학습한 뱀 게임 인공지능
강화학습 개요
강화학습의 목표는 에이전트가 환경을 탐색하면서 보상을 최대화할 수 있는 정책을 찾는 것이라고 할 수 있습니다. 매 시점 $t$에 에이전트(agent)는 자신의 상태(state) $s_t \in S$와 가능한 행동 집합(action space) $A(s_t)$를 가지고 있습니다. 에이전트가 행동(action) $a_t \in A(s_t)$를 수행하면 환경(environment)으로부터 다음 상태인 $s_{t+1}$를 확인하고 보상(reward) $r_t\in \mathbb{R}$를 받습니다. 보통 미래의 보상은 할인율(discount factor) $\gamma$를 곱해서 계산하는데 현재로부터 $\Delta t$ 이후에 주어지는 보상은 현재 가치로 환산할 때 $\gamma^{\Delta t}$를 곱해줍니다. 에이전트는 환경과의 상호작용으로부터 할인된 보상의 총합을 최대화할 수 있는 정책(policy)을 찾게 됩니다.

벰 게임을 플레이하는 상황을 예로 들면 강화학습의 각 구성요소를 다음과 같이 대응시킬 수 있습니다.
- 에이전트: 플레이어
- 환경: 게임기
- 상태: 필드 모양, 뱀 길이, 뱀의 진행 방향 등
- 보상: 점수
- 행동: 뱀의 전진, 방향 전환
뱀 게임 디자인
이번 절에서는 강화학습을 적용할 수 있도록 뱀 게임을 좀더 명확하게 정의하고, 이를 구현하는 방법에 대해 알아보겠습니다.
뱀 게임 규칙
뱀 게임은 1970년대에 처음 등장해서 지금까지 다양한 형태의 변종이 존재합니다. 이번 프로젝트에서는 강화학습의 효과를 쉽게 확인하기 위해서 간단한 형태의 뱀 게임 환경을 구현하겠습니다. 우리의 뱀 게임은 다음과 같은 규칙을 따라 진행됩니다.
- $m \times n$ 크기의 필드가 주어집니다. 각 칸은 비어 있거나 장애물, 먹이, 혹은 뱀의 일부로 이루어져 있습니다. 뱀은 하나의 실 형태로 존재합니다.
- 뱀은 일정 시간마다 앞, 왼쪽, 오른쪽 방향 중 하나를 선택해 움직입니다. 이때, 몸통 부분은 고정되어 있고 머리 부분이 늘어나고 꼬리 부분이 줄어듭니다.
- 뱀이 장애물 혹은 자신의 몸통에 부딪히거나 필드 밖으로 나가면 게임이 종료됩니다.
- 뱀이 먹이에 닿으면 길이가 증가합니다. 이때, 먹이는 빈 칸 중 하나에 무작위로 생성됩니다.
게임의 목표는 뱀을 최대한 길어지게 만드는 것입니다. 이를 위해서 뱀이 자신의 몸통과 장애물을 피해가면서 먹이를 많이 먹을 수 있도록 이동하는 전략이 필요할 것입니다.
블록
블록의 종류로는 빈 칸, 장애물, 먹이, 뱀의 머리, 뱀의 몸통, 뱀의 꼬리가 있습니다. 빈 칸, 장애물, 먹이 블록은 각각 하나의 형태만 존재하지만 뱀의 머리, 몸통, 꼬리 블록은 각각 방향에 따라 다양한 형태를 가지고 있습니다.
| 종류 | 빈 칸 | 방해물 | 먹이 | 뱀 머리 | 뱀 몸통 | 뱀 꼬리 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 번호 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 형태 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
각 블록은 번호, 색깔, 폴리곤을 이루는 점들 정보를 가지고 있습니다. 번호는 필드를 뉴럴넷 입력 값으로 임베딩할 때 원-핫 인코딩하는 데에 사용되고 색깔과 점들 정보는 랜더링할 때 사용됩니다.
class Block:
@staticmethod
def contains(**args):
pass
@staticmethod
def get_code(**args):
pass
@staticmethod
def get_color(**args):
pass
@staticmethod
def get_points(**args):
pass
실제 구현에서는 블록 종류별로 위의 block을 상속받아서 클래스를 만들고 각 함수를 따로 구현했습니다. 폴리곤 모양을 하드 코딩해서 구현했기 때문에 코드가 상당히 깁니다. 자세한 내용은 깃헙 코드를 참고해 주세요.
뱀
아래 그림은 필드의 좌표계와 방향의 번호를 나타냅니다. 뱀은 꼬리의 위치와 꼬리에서 시작해서 뱀의 머리가 뻗어나간 방향의 수열로 나타낼 수 있습니다. 예를 들어 그림에 있는 뱀은 꼬리 위치 (4, 1)과 방향 수열 [0, 0, 1, 1, 0, 1, 1, 2, 2, 1, 2, 1, 1, 0, 3]로 나타낼 수 있습니다.
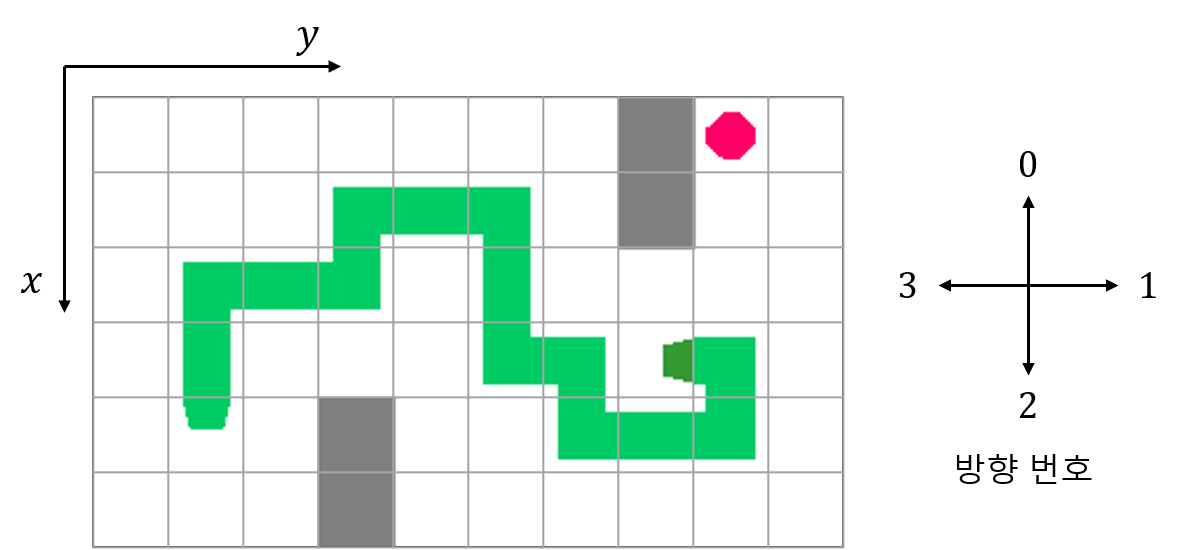
방향 수열에서 첫 번째 수는 꼬리의 방향을 나타내고 마지막 수는 머리의 방향을 나타냅니다. 또한, 수열에서 각 연속한 방향 쌍으로 뱀의 몸통을 나타낼 수 있습니다.
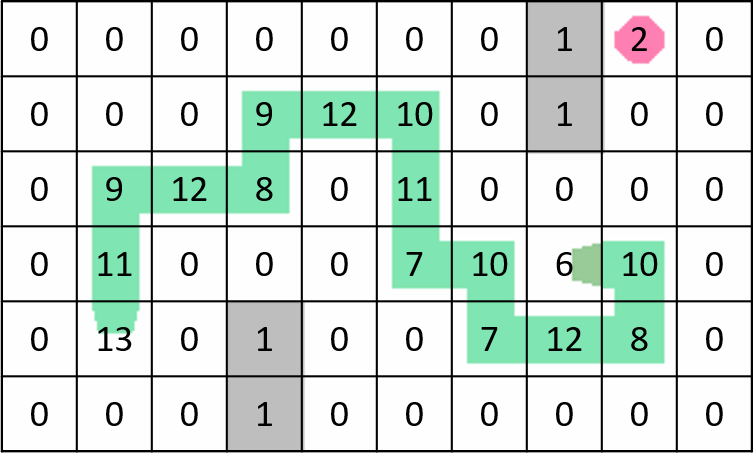
위의 뱀을 예시로 들어보겠습니다. 방향 수열의 첫 번째 수는 0으로 꼬리의 연결부가 위를 향하게 됩니다. 그리고 방향 수열의 마지막 수는 3으로 머리가 왼쪽을 향하게 됩니다. 방향 수열에서 연속된 모든 쌍은 (0, 0), (0, 1), (1, 1), …, (1, 1), (1, 0), (0, 3)이고 이들은 각각 뱀 몸통인 11, 9, 12, …, 7, 12, 8번 블록과 대응됩니다. 아래 그림은 필드의 각 블록에 해당하는 번호를 나타냅니다.
행동
일정 시간마다 에이전트는 MOVE_FORWARD, TURN_LEFT, TURN_RIGHT 총 세가지 중 하나의 행동을 선택해야 합니다. 에이전트가 MOVE_FORWARD를 선택하면 뱀이 진행방향으로 한 칸 전진합니다. TURN_LEFT를 선택하면 뱀이 시계방향으로 90도 회전한 후 한 칸 전진하고, TURN_RIGHT를 선택하면 뱀이 시계방향으로 90도 회전한 후 한 칸 전진합니다. 각 행동의 번호는 다음과 같이 정의되어 있습니다.
class SnakeAction:
MOVE_FORWARD = 0
TURN_LEFT = 1
TURN_RIGHT = 2
보상
에이전트는 행동을 선택할 때마다 보상을 받게 됩니다. 선택한 행동에 의해 게임이 종료되었다면 -1, 먹이를 먹지 않고 이동을 했다면 0의 보상을 얻습니다. 뱀의 길이가 증가할수록 먹이를 얻기 힘들어지는 점을 고려하여 먹이를 먹은 경우 최종 뱀의 길이를 보상으로 얻도록 만들었습니다.
상태
강화학습을 하기 위해서는 환경에서 발생되는 모든 정보를 알 수 있도록 상태를 정의하는 것이 좋습니다. 놀랍게도 우리가 정의한 뱀 게임은 필드 정보만을 가지고도 모든 정보를 알 수 있습니다. 다시 말해, $i$번째 필드를 $s_i$라고 할 때 다음이 성립합니다.
$\mathbb{P}(s_{t+1} \mid s_t) = \mathbb{P}(s_{t+1} \mid s_1, …, s_t)$
참고로 우리가 단 하나의 블록을 사용해서 뱀을 나타냈다면 위 식이 성립하지 않습니다. 초록색 블럭으로 뱀을 나타냈을 때 $i$번째 필드를 $s’_i$라고 정의하겠습니다. 다음과 같은 상황을 생각해보세요.

$s’_1, s’_2$ 모두를 관찰했다면 (2, 1)에 뱀의 머리가 있다(어느 쪽을 향하고 있는지는 알 수 없습니다)는 사실을 알 수 있지만 $s’_2$만 관찰하면 네 블록 중 어느 블록에 뱀의 머리가 있는지 알 수 없습니다. 따라서 $\mathbb{P}(s’_3 \mid s’_2) \neq \mathbb{P}(s’_3 \mid s’_1, s’_2)$가 됩니다. 이 문제는 뱀의 머리와 나머지 부분을 따로 구분하는 것만으로는 해결되지 않습니다. 필드를 통해 모든 정보를 얻을 수 있도록 하려면 필드 안에 뱀의 모양과 진행 방향 등의 정보가 모두 포함되어 있어야 합니다.
뱀의 모양과 관련된 정보를 필드 안에 포함하지 않고 따로 피쳐를 만드는 것을 고려할 수도 있습니다. 하지만, 이 경우에는 다른 두 유형의 피쳐를 학습할 수 있도록 복잡한 뉴럴넷을 설계해야 하므로 간단히 강화학습을 테스트하자는 취지와 맞지 않는다고 보았습니다. 여러가지를 고려한 결과, 필드 정보만 상태로 정의해도 괜찮도록 이전 절에서 소개한 방식으로 뱀을 디자인했습니다.
전이
에이전트가 선택할 수 있는 총 세 가지의 행동(MOVE_FORWARD, TURN_LEFT, TURN_RIGHT)에 따라 상태를 적절히 변화시켜야 합니다. 이를 쉽게 구현하기 위해서 필드 정보 이외에도 뱀 머리의 위치, 뱀 꼬리의 위치, 방향 수열, 뱀의 현재 진행 방향을 변수로 저장하였습니다.
TURN_LEFT를 수행하는 것은 뱀의 현재 진행 방향을 왼쪽으로 변경하고 MOVE_FORWARD를 수행하는 것과 같습니다. 마찬가지로 TURN_RIGHT는 현재 진행 방향을 오른쪽으로 변경하고 MOVE_FORWARD를 수행하는 것과 같을 것입니다. 따라서 MOVE_FORWARD에 따른 상태 변화를 구현하면 나머지 두 행동에 따른 생태 변화는 앞에 방향 전환을 추가하는 식으로 쉽게 구현할 수 있습니다.
MOVE_FORWARD를 수행해서 뱀이 이동할 때 뱀의 모든 부분을 다시 수정할 필요는 없습니다. 움직이는 형태를 보면 뱀의 앞부분과 뒷부분에만 변화가 있고 뱀의 중간 부분은 변하지 않기 때문입니다. 뱀의 머리와 꼬리 모양은 뱀의 방향 수열을 업데이트했을 때 바뀌는 부분에 맞춰 수정해주면 됩니다. 다음과 같이 몇 가지 경우를 고려해서 상태를 변화시킵니다.
- 뱀 머리의 진행 방향에 벽, 장애물, 뱀 몸통이 있는 경우 게임을 종료합니다. 뱀의 꼬리가 있는 경우는 상관없다는 점에 주의합시다.
- 뱀 머리의 진행 방향에 먹이가 없는 경우 뱀의 머리와 꼬리를 옮깁니다.
- 뱀 머리의 진행 방향에 먹이가 있는 경우 뱀의 머리만 옮기고 새로운 먹이를 생성합니다.
상태와 전이를 다루는 부분은 SnakeStateTransition 클래스에서 확인할 수 있습니다. get_state 함수는 상태를 리턴하는 함수로 필드를 원-핫 인코딩하여 제공합니다. 따라서 상태의 크기는 (높이)$\times$(너비)$\times$17이 됩니다. move_forward, turn_left, turn_right는 전이 관련 함수로 상태변화에 따른 보상과 게임 종료 여부를 리턴합니다.
class SnakeStateTransition:
DX, DY = [-1, 0, 1, 0], [0, 1, 0, -1]
def __init__(self, field_size, field, num_feed, initial_head_position, initial_tail_position, initial_snake):
self.field_height, self.field_width = field_size
self.field = field.copy()
self.hx, self.hy = initial_head_position
self.tx, self.ty = initial_tail_position
self.snake = deque(initial_snake)
self.direction = initial_snake[-1]
for _ in range(num_feed):
self._generate_feed()
def _generate_feed(self):
empty_blocks = []
for i in range(self.field_height):
for j in range(self.field_width):
if self.field[i][j] == EmptyBlock.get_code():
empty_blocks.append((i, j))
if len(empty_blocks) > 0:
x, y = random.sample(empty_blocks, 1)[0]
self.field[x, y] = FeedBlock.get_code()
def get_state(self):
return np.eye(NUM_CHANNELS)[self.field]
def get_length(self):
return len(self.snake) + 1
def move_forward(self):
hx = self.hx + SnakeStateTransition.DX[self.direction]
hy = self.hy + SnakeStateTransition.DY[self.direction]
if hx < 0 or hx >= self.field_height or hy < 0 or hy >= self.field_width \
or ObstacleBlock.contains(self.field[hx][hy]) \
or SnakeBodyBlock.contains(self.field[hx][hy]):
return -1, True
is_feed = FeedBlock.contains(self.field[hx][hy])
if not is_feed:
self.field[self.tx, self.ty] = EmptyBlock.get_code()
td = self.snake.popleft()
self.tx += SnakeStateTransition.DX[td]
self.ty += SnakeStateTransition.DY[td]
self.field[self.tx, self.ty] = SnakeTailBlock.get_code(self.snake[0])
self.snake.append(self.direction)
self.field[self.hx, self.hy] = SnakeBodyBlock.get_code(self.snake[-1], self.snake[-2])
self.field[hx, hy] = SnakeHeadBlock.get_code(self.snake[-1])
self.hx, self.hy = hx, hy
if is_feed:
self._generate_feed()
return self.get_length(), False
return 0, False
def turn_left(self):
self.direction = (self.direction + 3) % 4
return self.move_forward()
def turn_right(self):
self.direction = (self.direction + 1) % 4
return self.move_forward()
환경
환경 클래스는 OpenAI의 gym 라이브러리 스타일로 구현했습니다. reset 함수는 초기 상태를 리턴하고, step 함수는 행동을 입력받고 변화된 상태, 보상, 게임 종료 여부를 리턴합니다. render 함수는 현재 상태를 이미지로 만들어 화면에 출력하는 역할을 합니다. 필드를 출력하기 위해 필드의 각 블록 번호를 가지고 색깔, 점들 위치를 가져오고 pygame의 함수를 이용하여 폴리곤을 그립니다.
class Snake:
ACTIONS = {
SnakeAction.MOVE_FORWARD: 'move_forward',
SnakeAction.TURN_LEFT: 'turn_left',
SnakeAction.TURN_RIGHT: 'turn_right'
}
def __init__(self, level_loader, block_pixels=30):
self.level_loader = level_loader
self.block_pixels = block_pixels
self.field_height, self.field_width = self.level_loader.get_field_size()
pygame.init()
self.screen = pygame.display.set_mode((
self.field_width * block_pixels,
self.field_height * block_pixels
))
self.clock = pygame.time.Clock()
self.reset()
def reset(self):
self.state_transition = SnakeStateTransition(
self.level_loader.get_field_size(),
self.level_loader.get_field(),
self.level_loader.get_num_feed(),
self.level_loader.get_initial_head_position(),
self.level_loader.get_initial_tail_position(),
self.level_loader.get_initial_snake()
)
self.tot_reward = 0
return self.state_transition.get_state()
def step(self, action):
reward, done = getattr(self.state_transition, Snake.ACTIONS[action])()
self.tot_reward += reward
return self.state_transition.get_state(), reward, done
def get_length(self):
return self.state_transition.get_length()
def quit(self):
pygame.quit()
def render(self, fps):
pygame.display.set_caption('length: {}'.format(self.state_transition.get_length()))
pygame.event.pump()
self.screen.fill((255, 255, 255))
for i in range(self.field_height):
for j in range(self.field_width):
cp = get_color_points(self.state_transition.field[i][j])
if cp is None:
continue
pygame.draw.polygon(
self.screen,
cp[0],
(cp[1] + [j, i])*self.block_pixels
)
pygame.display.flip()
self.clock.tick(fps)
def save_image(self, save_path):
pygame.image.save(self.screen, save_path)
Deep Q-learning 적용
우리가 정의한 뱀 게임에서는 상태로 필드 정보와 같은 고차원의 입력값이 주어집니다. 이러한 상황에서 정책을 학습시킬 수 있는 강화학습 알고리즘 중 하나인 deep q-learning에 대해서 알아보고 뱀 게임에 적용시켜봅시다.
에이전트의 목표는 다음과 같이 정의되는 할인된 보상의 총합을 최대화하는 것입니다.
$R_t = \sum_{t’=t}^T \gamma^{t’-t}r_{t’}$
행동-가치 함수(action-value function) $Q(s, a)$는 어떤 정책 $\pi$을 따를 때, 상태 $s$를 보고 행동 $a$를 수행했을 때의 보상 기댓값으로 정의합니다. 그리고 최적 행동-가치 함수(optimal action-value function) $Q^\ast(s, a)$는 상태 $s$를 보고 행동 $a$를 수행했을 때 보상 기댓값의 최댓값으로 정의됩니다.
$Q^\pi(s, a) = \mathbb{E}_\pi[R_t \mid S_t=s, a_t=a]$
$Q^\ast(s, a) = max_\pi Q^\pi(s, a)$
최적의 정책 $\pi^\ast(s)$는 주어진 상태 $s$에서 $Q^\ast(s, a)$가 최대가 되도록 하는 행동 $a$를 선택하는 것이라고 할 수 있으므로 다음과 같이 나타낼 수 있습니다.
$\pi^\ast(s) = \underset{a}{\operatorname{argmax}} Q^\ast(s, a)$
우리는 $Q^\ast$를 직접 구할 수 없습니다. 벨만 방정식으로 $Q^\ast$의 현재 상태 $s$에 대한 값과 다음 상태 $s’$에 대한 값간의 관계를 이끌어냅시다.
$Q^\ast(s,a) = \mathbb{E_{s’\sim\varepsilon }}[r+\gamma \max_{a’}Q^\ast(s’, a’) \mid S_t=s, a_t=a]$
그러면 다음과 같이 반복적인 업데이트가 가능한 형태로 변형이 가능하고 $i$가 커질 때 $Q_i$가 $Q^\ast$에 수렴하도록 만들 수 있습니다.
$Q_{i+1}(s,a) = \mathbb{E_{s’\sim\varepsilon }}[r+\gamma \max_{a’}Q_i(s’, a’) \mid S_t=s, a_t=a]$
하지만, 이 방법은 아주 큰 공간을 요구하기 때문에 그대로 사용하기는 어렵습니다. 이를 해결하기 위해 최적 행동-가치 함수 $Q^\ast(s, a)$를 가중치가 $\theta$인 뉴럴 네트워크 함수 $Q(s, a; \theta)$로 근사할 것입니다. 다음과 같이 정의되는 손실 함수 $L_i(\theta_i)$를 경사 하강법(gradient descent)으로 최소화하여 뉴럴 네트워크를 학습합니다.
$L_i(\theta_i) = \mathbb{E_{s, a\sim\rho(\cdot)}}[(y_i-Q(s, a; \theta_i))^2]$
where $y_i = \mathbb{E_{s’ \sim \varepsilon}}[r+\gamma \max_{a’}Q(s’, a’; \theta_{i-1}) \mid s, a]$
Experience Replay
Deep Q-learning은 일반적인 Q-learning과 다르게 매 스탭마다 ($s_t$, $a_t$, $r_t$, $s_{t+1}$) 정보(experience)를 replay memory에 저장하고 학습시 균등 분포(uniform distribution)에 따라 샘플링하여 사용했습니다. 이 방식은 experience가 여러번 사용될 수 있게 만들기 때문에 데이터의 효율성을 높여줍니다. 또한, 연속적인 샘플 사이에는 높은 상관관계를 가지는데 샘플들을 랜덤으로 뽑아서 사용하기 때문에 분산을 줄일 수 있습니다.
Fixed Q Target
지도 학습(supervised learning)을 할 때 타겟을 고정시키는 것과 마찬가지로 $L_i(\theta_i)$를 최소화할 때도 $y_i$의 파라매터인 $\theta_{i-1}$을 고정하면서 $\theta_i$를 최적화합니다. 즉, $Q(s, a; \theta_i)$를 나타내는 지역 네트워크를 학습할 때 $Q(s’, a’; \theta_{i-1})$을 나타내는 타겟 네트워크를 따로 두어 가중치를 고정시킵니다. 그리고 일정 스탭마다 지역 네트워크의 가중치를 타겟 네트워크에 전달합니다. 이렇게 학습을 하면 타겟과 추정값 차이를 좁힐 때 타겟이 학습되고 있는 파라메터의 영향을 받지 않아 더 안정적인 학습이 가능할 것입니다.
Q-Networks
Q 함수는 컨볼루션 뉴럴 네트워크(convolutional neural network)를 사용하여 나타냅니다. 벰 게임에 사용한 뉴럴 네트워크는 (높이)$\times$(너비)$\times$17 크기로 임베딩된 필드 정보를 입력값으로 받고 각 행동에 대한 가치를 표현하는 벡터를 출력값으로 내놓습니다. 뉴럴 네트워크의 각 층은 다음과 같이 쌓았습니다.
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 7, 7, 32) 4928
_________________________________________________________________
dropout_1 (Dropout) (None, 7, 7, 32) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 5, 5, 32) 9248
_________________________________________________________________
dropout_2 (Dropout) (None, 5, 5, 32) 0
_________________________________________________________________
flatten_1 (Flatten) (None, 800) 0
_________________________________________________________________
dense_1 (Dense) (None, 256) 205056
_________________________________________________________________
dropout_3 (Dropout) (None, 256) 0
_________________________________________________________________
dense_2 (Dense) (None, 3) 771
=================================================================
Total params: 220,003
Trainable params: 220,003
Non-trainable params: 0
_________________________________________________________________
학습
이제 Deep Q-learning의 학습 과정을 살펴보겠습니다. 게임을 시작해서 끝날 때까지의 전체 과정을 에피소드(episode)라고 합니다. 한 에피소드를 시행하면 초기 상태를 확인한 다음, 종결(terminal) 상태가 아닐 때까지 행동을 선택하고 그에 따른 보상과 변화된 상태를 확인하는 과정을 반복합니다. 이러한 에피소드를 여러번 반복해서 학습이 이루어집니다.
에피소드를 학습할 때 탐색(exploration)과 활용(exploitation)의 균형을 맞추기 위해 $\epsilon$-greedy라는 간단한 알고리즘을 사용합니다. 만약 학습이 덜 된 상태에서 에이전트가 항상 최적으로 보이는 행동만 선택한다면 다른 행동을 선택했을 때 더 좋은 보상을 얻을 수 있는 경우를 고려하지 못 하게 됩니다. $\epsilon$-greedy는 이 문제를 해결하기 위해 $\epsilon$ 확률로 무작위로 행동을 선택하고 나머지 $1-\epsilon$ 확률로 그리디한 행동을 선택합니다. 논문에서는 학습 초기에 $\epsilon$을 1로 놓고 0.1까지 천천히 감소시키면서 충분한 탐색이 이루어지도록 하였습니다.
$\epsilon$-greedy에 따라 선택된 행동 $a_t$을 수행하면 새로운 상태 $s_{t+1}$, 보상 $r_t$, 종결 여부 $e_t$를 확인할 수 있습니다. $(s_t, a_t, r_t, s_{t+1}, e_t)$를 replay memory에 저장하고 샘플을 학습합니다. 논문에서는 타겟 네트워크를 일정 스탭마다 가중치를 업데이트하였습니다. 하지만, 에피소드 진행 중에 타겟의 가중치가 바뀌면 학습이 불안정해질 것 같아서 일정 에피소드 수마다 타겟 네트워크의 가중치를 업데이트하였습니다.
class DQNTrainer:
...
def train(self):
pbar = tqdm(initial=self.current_episode, total=self.episodes, unit='episodes')
while self.current_episode < self.episodes:
current_state = self.env.reset()
done = False
steps = 0
while not done and steps < self.max_steps:
if random.random() > self.epsilon:
action = np.argmax(self.agent.get_q_values(np.array([current_state])))
else:
action = np.random.randint(NUM_ACTIONS)
next_state, reward, done = self.env.step(action)
self.agent.update_replay_memory(current_state, action, reward, next_state, done)
self.summary.add('loss', self.agent.train())
current_state = next_state
steps += 1
self.agent.increase_target_update_counter()
self.summary.add('length', self.env.get_length())
self.summary.add('reward', self.env.tot_reward)
self.summary.add('steps', steps)
# decay epsilon
self.epsilon = max(self.epsilon-self.epsilon_decay, self.min_epsilon)
self.current_episode += 1
# save model, training info
if self.enable_save and self.current_episode % self.save_freq == 0:
self.save(str(self.current_episode))
average_length = self.summary.get_average('length')
if average_length > self.max_average_length:
self.max_average_length = average_length
self.save('best')
print('best model saved - average_length: {}'.format(average_length))
self.summary.write(self.current_episode, self.epsilon)
self.summary.clear()
# update pbar
pbar.update(1)
# preview
if self.enable_render and self.current_episode % self.render_freq == 0:
self.preview(self.render_fps)
...
replay memory는 deque 자료구조를 사용해서 일정 개수까지만 저장할 수 있도록 하였습니다. 학습 시 replay memory에서 $(s_j, a_j, r_j, s_{j+1}, e_j)$를 샘플링해서 $Q$ 함수를 업데이트합니다. $e_j$이 종결 상태를 나타낼 때 타겟 값을 $r_j$로 놓고 그렇지 않은 경우에는 타겟 값을 구하기 위해 타겟 네트워크를 이용해 $r_j+\gamma \max_{a’}Q(s_{j+1}, a’; \theta)$을 계산합니다. 마지막으로 지역 네트워크의 추정값 $Q(s_j, a_j; \theta)$과 타겟 값의 차이를 작게 만들도록 지역 네트워크를 업데이트합니다.
class DQNAgent:
def __init__(self, field_size, gamma, batch_size, min_replay_memory_size, replay_memory_size, target_update_freq):
self.gamma = gamma
self.field_height, self.field_width = field_size
self.batch_size = batch_size
self.min_replay_memory_size = min_replay_memory_size
self.target_update_freq = target_update_freq
self.model = self._create_model()
self.target_model = self._create_model()
self.target_model.set_weights(self.model.get_weights())
self.model.summary()
self.replay_memory = deque(maxlen=replay_memory_size)
self.target_update_counter = 0
def _create_model(self):
model = Sequential([
Conv2D(32, (3, 3), input_shape=(self.field_height, self.field_width, NUM_CHANNELS), activation='relu'),
Dropout(0.1),
Conv2D(32, (3, 3), activation='relu'),
Dropout(0.1),
Flatten(),
Dense(256, activation='relu'),
Dropout(0.1),
Dense(NUM_ACTIONS)
])
model.compile(optimizer='rmsprop', loss='mse')
return model
def update_replay_memory(self, current_state, action, reward, next_state, done):
self.replay_memory.append((current_state, action, reward, next_state, done))
def get_q_values(self, x):
return self.model.predict(x)
def train(self):
# guarantee the minimum number of samples
if len(self.replay_memory) < self.min_replay_memory_size:
return
# get current q values and next q values
samples = random.sample(self.replay_memory, self.batch_size)
current_input = np.stack([sample[0] for sample in samples])
current_q_values = self.model.predict(current_input)
next_input = np.stack([sample[3] for sample in samples])
next_q_values = self.target_model.predict(next_input)
# update q values
for i, (current_state, action, reward, _, done) in enumerate(samples):
if done:
next_q_value = reward
else:
next_q_value = reward + self.gamma * np.max(next_q_values[i])
current_q_values[i, action] = next_q_value
# fit model
hist = self.model.fit(current_input, current_q_values, batch_size=self.batch_size, verbose=0, shuffle=False)
loss = hist.history['loss'][0]
return loss
def increase_target_update_counter(self):
self.target_update_counter += 1
if self.target_update_counter >= self.target_update_freq:
self.target_model.set_weights(self.model.get_weights())
self.target_update_counter = 0
def save(self, model_filepath, target_model_filepath):
self.model.save(model_filepath)
self.target_model.save(target_model_filepath)
def load(self, model_filepath, target_model_filepath):
self.model = keras.models.load_model(model_filepath)
self.target_model = keras.models.load_model(target_model_filepath)
결과
잘 학습된 결과 몇 가지를 뽑아 보았습니다. 길어진 몸을 다루기 위해 벽을 탄다거나 지그재그로 꺽는 등의 전략을 배우는 것을 확인할 수 있었습니다.

9x9 empty

9x9 obstacles