GNN의 시간 복잡도와 공간 복잡도
GNN , GCN , complexity , ClusterGCN
Introduction
우리가 흔히 알고 있는 인공 신경망에는 가장 기본적인 Fully-connected network 그리고 Convolutional Neural network (CNN)나 Recurrent Neural network (RNN) 등이 있습니다. 이러한 인공 신경망들은 보통 벡터나 행렬 형태로 input이 주어집니다. 하지만 input이 그래프인 경우에는 벡터나 행렬 형태로 나타내는 대신에 Graph Neural Network (GNN)를 사용할 수 있습니다.
지난 글에서 이미 GNN의 기본 원리와 간단한 예시에 대해서 알아보았기 때문에, 이번에는 조금 다른 주제에 대해서 다뤄보려고 합니다. (만약 읽지 않으셨다면, 위의 ‘지난 글’을 클릭하여 읽고 오시는 것을 권장합니다.) 이 글에서는 GNN의 시간 및 공간 복잡도와 이를 줄이기 위한 여러 가지 아이디어 중 KDD 2019에 발표된 ClusterGCN에 대해서 알아보도록 하겠습니다.
GCN의 시간 복잡도와 공간 복잡도
먼저 가장 기본적인 구조인 Graph Convolutional Network (GCN)의 경우부터 알아봅시다. 보통 인공신경망을 학습하는 데에는 경사 하강법 (Gradient Descent)를 많이 사용합니다. 경사 하강법은 다시 batch를 어떻게 설정하냐에 따라서 Full-batch gradient descent와 Mini-batch SGD로 나뉘어집니다. 복잡도를 나타내기 위해서 $N$과 $M$을 각각 그래프에서의 노드의 수와 링크의 수, $D$를 embedding dimension, 그리고 $L$을 쌓은 GCN layer의 개수로 정의합시다.
Full-batch gradient descent
먼저 Full-batch gradient descent의 경우부터 알아봅시다. 이 경우에는 GCN의 한 레이어의 forward propagation을 아래와 같은 식으로 나타낼 수 있습니다.
$X^{(l+1)} = \sigma(A’X^{(l)}W^{(l+1)})$
위의 식에서 $X^{(l)}$은 $l$번째 layer를 거치고 난 후의 embedding, $A’$는 normalize를 거친 후의 인접 행렬, $W^{(l+1)}$은 $l+1$번째 layer의 학습 가능한 parameter, 그리고 $\sigma$는 sigmoid, ReLU 등의 활성화 함수를 의미합니다. $A’$는 sparse matrix이고 내부의 non-empty element의 수가 $M$ (무향 그래프인 경우에는 $2 \times M$) 이고, $W$는 $D \times D$의 shape를 가지기 때문에 한 epoch를 수행하는 시간 복잡도는 $O(L(MD + ND^2))$가 됩니다. 공간 복잡도의 경우에는 각 layer마다 parameter의 정보와 각 노드의 embedding을 가지고 있어야 하기 때문에 $O(L(D^2 + ND))$ 가 될 것입니다.
Mini-batch SGD
Mini-batch SGD의 복잡도를 분석하기 위해 mini-batch size를 $B$, 그리고 노드의 평균 degree를 $d$라고 합시다. (이 경우 $d \in O(\frac{N}{M})$이 성립할 것입니다.)
Mini-batch SGD를 사용하는 경우에는 한 배치 내에서 모든 노드를 볼 필요가 없어서 메모리 사용량을 줄일 수 있습니다. 그러나, 여전히 $L$-hop 내의 모든 노드를 봐야하는 문제가 있습니다. 먼저 $B$가 1인 경우를 생각해보면, 평균적으로 하나의 노드의 embedding을 update하기 위해서 살펴봐야할 노드의 개수를 $O(d^L)$로 볼 수 있습니다. 이 때의 공간 복잡도는 $O(L(d^L + D^2))$가 되고, 시간 복잡도의 경우에는 $N$번 반복해야 한 epoch가 완료되므로 한 epoch를 수행하는 시간은 $O(d^LND^2)$로 나타낼 수 있습니다. batch size가 B인 경우에는 최악의 경우 살펴봐야할 노드의 개수가 $O(Bd^L)$개가 되므로, 시간 복잡도는 변하지 않고 공간 복잡도만 $O(L(Bd^L + D^2))$로 변합니다.
Mini-batch SGD with Neighborhood sampling
위에서처럼, 하나의 노드의 embedding을 update하기 위해서 필요한 노드의 개수는 layer의 개수가 많아질수록 exponential하게 증가합니다. 이러한 급격한 증가를 막기 위한 방법으로 neighborhood sampling을 고려할 수 있고, 대표적으로 사용한 사례로 GraphSAGE가 있습니다. Neighborhood sampling을 사용하여 한 노드가 가질 수 있는 neighbor의 수를 최대 $r$개로 고정할 수 있습니다.
이 때, 하나의 노드의 embedding을 update하기 위해서 살펴봐야할 노드의 개수는 $O(r^L)$이 됩니다. 여전히 exponential하게 증가하지만, neighbor 개수를 제한함으로써 증가 폭을 줄일 수 있습니다. Neighborhood sampling을 도입했을 때의 시간 복잡도와 공간 복잡도는 각각 $O(r^LND^2)$과 $O(L(Br^L+D^2))$입니다. (복잡도를 계산하는 과정이 같기 때문에 $d$ 대신 $r$로 바뀐 것 외에 차이가 없습니다.)
ClusterGCN
앞서 언급했듯이, Mini-batch SGD에서 한 배치를 update할 때 살펴봐야할 노드의 개수는 minibatch 내의 노드와 연결된 모든 링크가 batch 내부에 존재하는 경우에는 $O(BL)$이 되겠지만, 최악의 경우 $O(Bd^L)$이 될 수도 있습니다. 즉, minibatch가 어떻게 이루어지느냐에 따라 시간 복잡도가 크게 달라질 수 있습니다.
그렇다면 어떻게 노드의 연결된 링크들이 최대한 batch 내에 있는 노드와 연결되도록 할 수 있을까요? ClusterGCN의 저자들은 이 질문에 대한 해법으로 군집화 (Clustering)을 제안했습니다.
Vanilla ClusterGCN
ClusterGCN은 먼저 그래프를 클러스터링을 통해 $c$개의 subgraph로 나눈 후, 각 subgraph에 속한 노드를 batch로 하여 GCN 모델을 학습하는 구조를 가지고 있습니다. 특징이 있다면, 아래 그림처럼 ClusterGCN에서는 배치 내에 있는 노드와 배치 외부에 있는 노드 간의 연결을 무시합니다. 연결을 무시함으로써 minibatch를 update하는 시간을 줄이고, clustering을 통해서 연결을 무시함으로서 발생하는 성능 감소를 최소화하려고 했습니다.
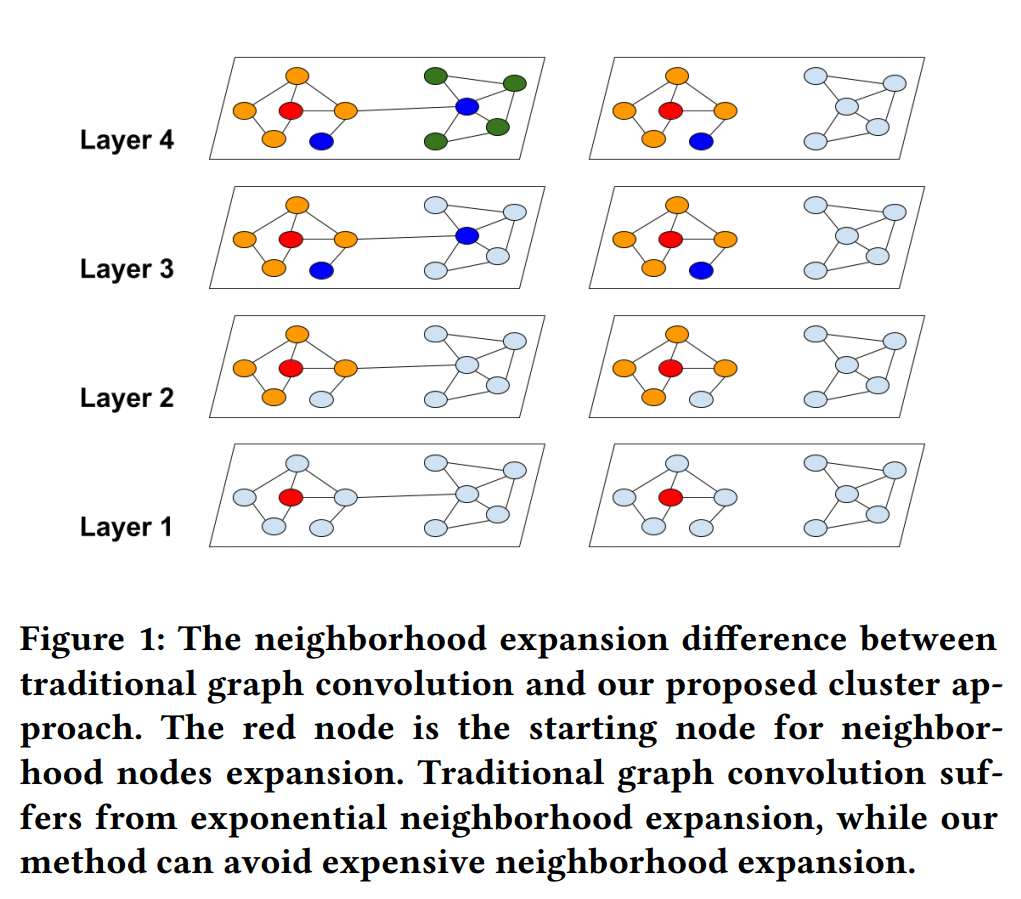
배치 내에 있는 노드와 배치 외부에 있는 노드 간의 연결을 무시하기 때문에, 무시하기 전 인접 행렬을 $A$라고 한다면, ClusterGCN에서의 인접 행렬은 아래와 같은 diagonal 형태의 block matrix로 나타낼 수 있고, embedding도 아래와 같이 쉽게 분해할 수 있습니다.
$\bar{A} = \begin{bmatrix} A_{11} & \cdots & 0 \ \vdots & \ddots & \vdots \ 0 & \cdots & A_{cc} \end{bmatrix}$
$X^{(l+1)} = \sigma(\bar{A}X^{(l)}W^{(l+1)}) = \begin{bmatrix} \sigma(\bar{A_{11}}X^{l}{1}W^{l+1}) \ \vdots \ \sigma(\bar{A{cc}}X^{l}_{c}W^{l+1}) \end{bmatrix}$
위의 식에서 $X^{l}_{i}$는 $X^{l}$의 $i$번째 클러스터에 해당하는 노드들의 embedding을 의미합니다. 마찬가지로 loss function도 아래와 같이 분해할 수 있게 된다는 장점을 가지고 있습니다.
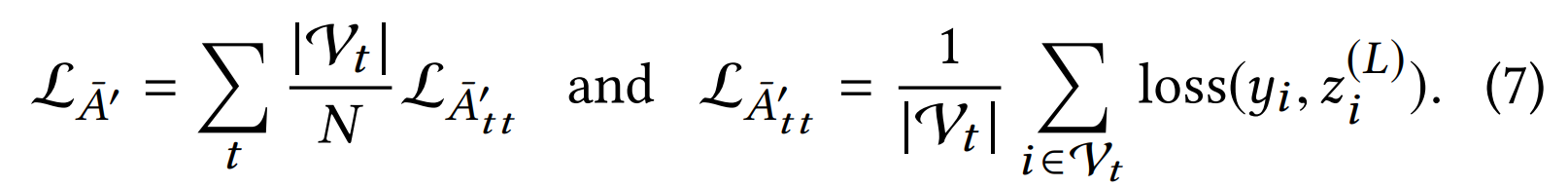
Vanilla ClusterGCN의 시간 복잡도와 공간 복잡도
$i$번째 클러스터에 속한 노드의 개수와 링크의 개수를 $v_i$, $e_i$라고 합시다. $i$번째 클러스터의 embedding을 update하는 과정은 Full-batch gradient descent와 완전히 같은 과정으로 이루어집니다.
Fully-batch gradient descent의 시간 복잡도와 공간 복잡도는 각각 $O(L(MD + ND^2))$, $O(L(D^2 + ND))$ 이므로, $i$번째 클러스터에 속한 노드의 embedding을 update하는 데 걸리는 시간 복잡도와 공간 복잡도는 각각 $O(L(e_i D + v_i D^2))$, $O(L(D^2 + v_iD))$ 가 됩니다. 그러므로, ClusterGCN에서 한 epoch를 업데이트하는 과정의 시간 복잡도와 공간 복잡도는 다음과 같습니다.
시간 복잡도: $\sum_{i=1}^{c} O(L(e_i D + v_i D^2)) = O(L(MD + ND^2))$
공간 복잡도: $\max_{i} O(L(D^2 + v_iD)) = O(L(D^2 + \max_{i} v_i D))$
시간 복잡도는 GCN과 완전히 같으면서도 공간 복잡도는 가장 효율적인 것을 확인할 수 있습니다.
Stochastic Multiple Partitions
Vanilla ClusterGCN은 시간 복잡도와 공간 복잡도가 모두 효율적이지만 아래의 단점을 가지고 있습니다.
- 그래프에서 클러스터링을 한 이후 서로 다른 클러스터에 있는 노드들 사이의 링크는 모두 무시합니다. 기존의 그래프에서 변형이 되므로 당연히 성능에 영향을 미치게 됩니다.
- 비슷한 노드들끼리 같은 클러스터에 묶이게 되므로, 기존의 random minibatch와 클러스터의 distribution이 서로 다른 현상이 벌어집니다. 예를 들어서, classification 문제의 경우 랜덤 배치에 비해서 클러스터의 label entropy가 상당히 작아지게 됩니다. 이에 따라 다른 batch 간의 variance가 증가하여 모델의 학습 속도에 영향을 주게 됩니다.
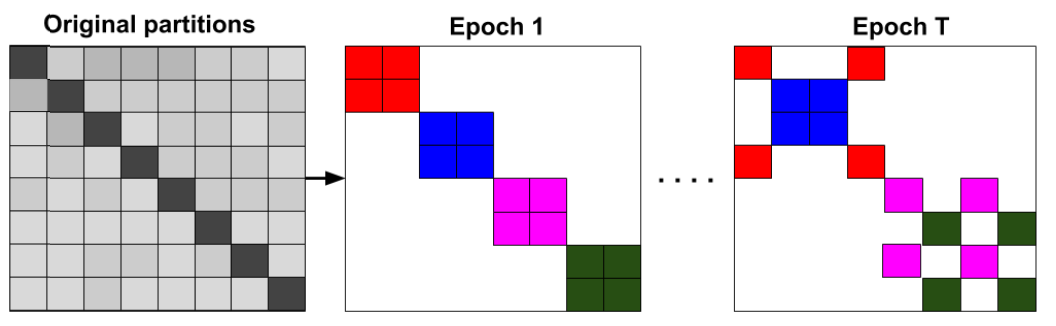
이러한 문제를 해결하기 위해 저자들은 알고리즘에 여러 변화를 주었습니다. 먼저, 한 클러스터 내에서만 학습하는 Vanilla 버전에 비해서, 개선된 알고리즘에서는 여러 클러스터를 묶어서 학습을 진행합니다. (대신, 클러스터링을 할 때 그래프를 조금 더 잘게 쪼개어 배치 크기는 변하지 않도록 합니다.) 그리고, 클러스터 내부의 연결을 제외한 모든 연결을 무시했던 것에 비해서, 묶인 클러스터에서의 무시되었던 연결은 모두 복구하고 학습을 진행합니다.
Experiments
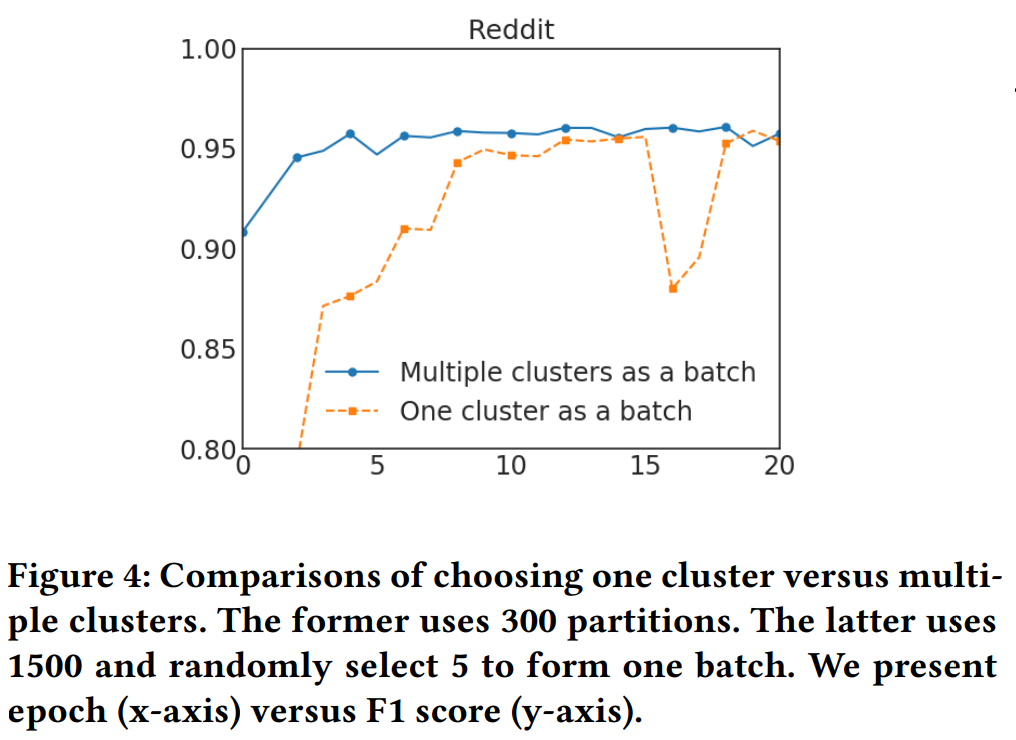
먼저 소개할 내용은 Vanilla ClusterGCN (One cluster as a batch)와 Stochastic Multiple Partitions (Multiple clusters as a batch)를 적용한 후를 비교한 실험 결과입니다. x축은 training epoch를, y축은 F1 score (높을수록 좋음)를 나타냅니다. 최종적인 F1 score는 비슷하지만, 후자가 학습 속도가 더 빠른 것을 확인할 수 있습니다.

위의 표는 사용한 여러 데이터 셋과 layer 개수를 다르게 했을 때의 메모리 사용량을 비교한 표입니다. ClusterGCN이 GraphSAGE를 비롯한 다른 모델들에 비해서 실험적으로도 메모리를 적게 사용하고 있음을 확인할 수 있습니다.
마무리
기본적으로 GCN에서 Full-batch gradient descent는 노드의 개수가 커지거나 링크의 수가 많아지면, 메모리 사용량이 지나치게 많아지는 문제가 있었고, mini-batch를 적용하면 한 epoch를 수행하는 속도가 느려지는 문제가 발생합니다.
이 글에서는 클러스터링 기법을 사용하여 한 epoch를 수행하는 속도는 Full-batch gradient descent와 같으면서도 메모리 사용량을 줄인 모델인 ClusterGCN에 대해서 알아보았습니다. 논문 링크는 Reference에 남겨두었고, 구현은 https://github.com/google-research/google-research/tree/master/cluster_gcn 에서 확인하실 수 있습니다.