De Bruijn 수열

당신은, 친구에게 $1$에서 $K$까지의 수들을 나열한 원형 수열(끝 글자와 첫 글자가 이어지는 수열)을 선물로 받았다. 그런데 이 수열은 신기한 성질을 가지고 있다. 이 수열에서 길이 $N$인 연속한 부분수열들을 모두 나열한다. 물론 원형 수열이기 때문에 그런 수열의 개수는 수열의 길이와 같다. 이 때, 이렇게 모은 부분수열의 모음이 그러면 $1$에서 $K$까지의 수들로 만든 모든 길이 $N$의 수열의 모음과 같았다!

그런 수열을 de Bruijn(‘jin’이 아니라 ‘ijn’임에 유의하자. 드 브루인이라고 읽는다.) 수열이라 한다. 예를 들어 $K = 3$, $N = 2$인 de Bruijn 수열 $B(3, 2) = ‘112322133’$을 보자. 이 수열의 길이 N = 2인 부분수열의 개수는 수열의 길이와 같은 9개이다. 이들 $’11’$, $’12’$, $’23’$, $’32’$, $’22’$, $’21’$, $’13’$, $’33’$, $’31’$(마지막은 De Bruijn 수열이 원형 수열이기 때문에 등장했다!)를 모두 모으면 $1$에서 $K = 3$까지의 수들로 이루어진 길이 $N = 2$의 수열을 순서 없이 모두 얻을 수 있다. 마찬가지로, $B(2, 3) = ‘11121222’$, $B(2, 4) = ‘1111211221212222’$ 등을 만들어낼 수 있다. 등호를 사용하였지만 물론 de Bruijn 수열이 유일하지는 않다. $B(2, 3) = ‘22212111’$도 가능한 선택지이다.

어떤 K와 N에 대한 De Bruijn 수열 B(K, N)의 이상적인 최소 길이는, 모든 가능한 길이 N의 부분수열의 개수와 같은, $L = K^N$이다. 물론 그러기 위해서는 운이 정말 좋아 길이 N의 부분수열들이 하나도 겹치지 않고 한 번씩만 나타나야 할 것이다. 놀랍게도 항상 최적으로 수열을 만드는 것이 가능하다. 증명은 아래에서 이런 수열을 실제로 만드는 방법을 보일 때 저절로 이루어질 것이다. 심지어 그런 방법의 가짓수도 굉장히 많은데, 서로 다른 De Bruijn 수열(돌려서 같은 것은 하나로 친다)의 개수는 아래와 같다:

$\frac{(k!)^{k^{n-1}}}{k^n}$

이제 우리의 주 관심사인, ‘어떻게 De Bruijn 수열을 만들 것인가’에 대해 생각해 보자.

De Bruijn 그래프

이 수열을 그래프로 그려보자. De Bruijn 그래프 $G(K, N) = (V, E)$는 다음과 같이 정의된다.

$S = \left\{1, \cdots, K \right\}$로 두면, $V = S^N$.
정점 $v_1$에 대한 수열의 맨 앞에서 수 하나를 없애고 맨 뒤에서 수 하나를 추가해서 정점 $v_2$에 대한 수열을 만들 수 있다면, $v_1 \rightarrow v_2$로 간선을 긋는다. 즉, $E = \left\{ \left(\left(s_i \right){i=1..N}, \left(s_i \right){i=2..N+1} \right) : s_i \in S, 1 \le i \le N+1 \right\}$. 조금 더 깔끔하게, 각 간선 위에 $s_{N+1} \in S$를 적어두자.

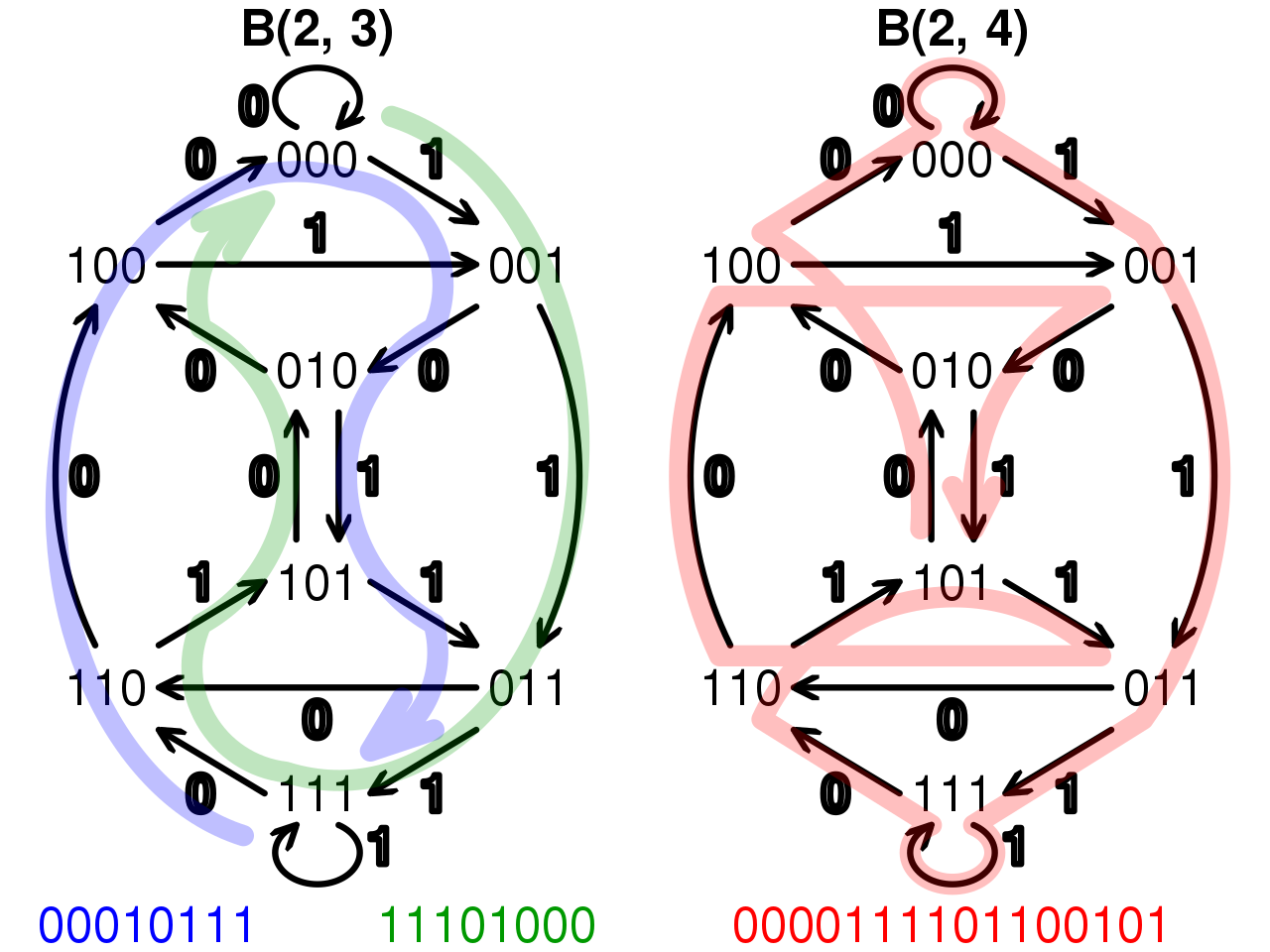
De Bruijn 그래프는,

정점이 $K^N$개이고 간선은 $K^{N+1}$개이다.
$G(K, N)$은 $G(K, N-1)$의 line graph이다. 이 때, 어떤 그래프 $(V, E)$의 line graph란, $(E, \left\{ ((v_1, v_2), (v_2, v_3)) : (v_1, v_2), (v_2, v_3) \in E \right\}$이다. 이 사실은, De Bruijn 그래프의 각 간선이 $(s_i)_{i=1..N+1}$에 대응됨을 생각해보면 매우 자연스럽다.
각 정점의 in-degree와 out-degree 모두 $K$이다. 따라서, 임의의 정점에서 시작하는 오일러 회로가 존재한다. 물론, De Bruijn 그래프는 다른 De Bruijn 그래프의 line graph이므로, 임의의 정점에서 시작하는 해밀턴 회로 또한 존재한다.

이 때, De Bruijn 그래프 $G(K, N)$의 오일러 회로 하나를 그리자. 그리고, 회로 위의 각 간선에 적힌 수를 쭉 이어 적어보자. 이때, 회로 위의 연속된 $N$개의 간선에 적힌 수들은 회로의 끝 정점에 적힌 수열과 같다. 모든 정점을 한 번씩만 지나므로, 이 오일러\ 회로는 De Bruijn 수열 $B(K, N)$에 대응된다. 오일러 회로를 찾는 Hierholzer 알고리즘은 간선의 개수에 대해 선형 시간에 작동하니, 우리는 De Bruijn 수열을 $O(K^{N+1}) = O(LK)$에 찾는 방법을 알아낸 것이다!

더 빠른 알고리즘

하지만 나이브하게 de Bruijn 그래프를 만드는 것은 굉장히 많은 메모리와 시간을 소모할 뿐더러, de Bruijn 수열을 만드는 도중에 멈출 수 없다는 문제가 있다. 그래프를 명시적으로 만드는 대신 정점을 나타내는 수열을 이용하여 암시적으로 만든 그래프에서 DFS를 수행하더라도 여전히 알고리즘은 매우 느린 시간에 작동한다. 이제, 목걸이와 Lyndon 단어라는 새로운 개념을 도입해, de Bruijn 수열을 가장 빠른 시간복잡도에 구할 수 있는 알고리즘을 소개한다. 이는 평균 $O(L)$의 시간복잡도에 작동한다.

아래 정의들에서, $K$를 고정한다. 따라서 사용할 수의 집합 $\{ 1, \cdots, K \}$도 고정된다. 이제 수열을 위 집합의 원소를 알파벳으로 하는 문자열로 보면, 문자열 $S$, $T$를 이어붙여 새로운 문자열 $ST$를 만들거나, 문자열 $S$를 $k$번 반복해 새로운 문자열 $S^k$를 만드는 연산을 그대로 할 수 있을 것이다. 또, $A = a_1 \cdots a_N$에 대해 $A_i = a_1 \cdots a_i$로 두자. 이제 우리가 알던 ‘사전순’의 개념을 여기서도 그대로 사용하자. 글자들 사이에는 글자를 나타내는 수의 대소관계를 그대로 적용시키기로 하고, $S < T$라는 것은 $S$가 $T$의 부분문자열이거나, $S = uav$, $T = ubw$이고 $a<b$를 만족하는 두 글자 $a$, $b$와 세 문자열 $u$, $v$, $w$가 존재한다는 것이라 하자.

정의 1. 문자열 $S=s_1 \cdots s_N$에 대해, $S$의 cyclic shift $S’ = s_i s_{i+1} \cdots s_N s_1 \cdots s_{i-1}$ ($1 < i \le N$)이 항상 $S < S’$를 만족한다면, 즉 $S$의 cyclic shift들의 집합에서 $S$가 사전순으로 제일 작은 단어일 때에 $S$를 목걸이(necklace)라고 한다. (사실은, $S$의 첫 글자와 끝 글자를 이은 목걸이 형태의 문자열을 사전순으로 가장 작은 선형 문자열 $S$로 대응시킨 것이다.)

모든 이야기는 “모든 목걸이들의 사전순 목록을 만드는 알고리즘을 어떻게 짤 수 있을까?”에서 시작한다. 가장 naive한 알고리즘은 다음과 같다.

$1$에서 $K$ 사이의 문자로 이루어진 길이 $N$의 문자열을 사전순으로 모두 만들어본다.
각각이 목걸이인지 검사하고, 목걸이이면 목록에 넣는다.

1번 과정은 아마 DFS를 통해 구현하게 될 것 같다. 따라서 위 알고리즘을 조금 더 자세히 설명하면 이렇게 된다.

DFS를 재귀적으로 수행한다. 깊이가 $d$인 DFS 함수는 길이 $d$인 문자열을 전달받고, 이 문자열의 끝에 글자를 하나 추가한 길이 $d+1$인 문자열 총 $K$개를 재귀적으로 전달한다.
DFS 함수가 깊이 $N$에 도달하면, 만들어진 수열이 목걸이인지 검사하고, 목걸이이면 목록에 넣는다.

위 알고리즘에서 검사하는 대부분의 수열은 목걸이가 아니기 때문에, 목걸이인지 검사하는 데에 상당히 많은 시간 낭비가 이루어진다. 위 알고리즘을 조금 더 ‘잘’ 구현할 수는 없을까?

정리 1. $A = a_1 \cdots a_N$이 목걸이이고 $a_i < K$일 때, $A_{i-1} (a_i+1)$도 목걸이이다.

증명. $A_{i-1} (a_i + 1)$이 목걸이가 아니라면, 인덱스 $k$가 존재하여,

$a_k \cdots a_{i-1} (a_i + 1) A_{k-1} < a_1 \cdots a_{i-1} (a_i - 1)$

을 만족할 것이다. 특히 $a_k \cdots a_{i-1} \le a_1 \cdots a_{i-k}$. 하지만 $A$가 목걸이라는 점에서 $a_k \cdots a_{i-1} \ge a_1 \cdots a_{i-k}$를 만족하므로 두 문자열은 길이 $i-k$의 접두사를 공유하고, $a_i - 1 \le a_{i-k+1}$, 즉 $a_i < a_{i-k+1}$여야만 한다. 따라서 $a_k \cdots a_i < a_1 \cdots a_{i-k+1}$이고, 이는 $A$가 목걸이임에 모순이다.

정리 2. 다음과 같이 $next$ 연산자를 정의한다. $A = a_1 \cdots a_N$이 어떤 $1 \le i \le N$에 대해 $a_i < a_{i+1} = \cdots = a_N = K$를 만족할 때, $next(A) = \left[ A_{i-1} (a_i - 1) \right] ^{\infty} _N$, 즉 $A _{i-1} (a _i - 1)$를 길이가 $N$이 될 때까지 반복한 문자열로 정의한다. 이 때, 목걸이 $A$에 대해 $A < B < next(A)$이면, $B$는 목걸이가 아니다.

증명. $B = b_1 \cdots b_N = A_{i-1} (a_i - 1) b_{i+1} \cdots b_N$ 꼴이 된다. $B$가 목걸이라고 하자. 그러면 $B \le b_{i+1} \cdots b_N$이므로 $A_{i-1} (a_i - 1) \le b_{i+1} \cdots b_{2i}$. 한편, $B < next(A)$에서 $b_{i+1} \cdots b_{2i} \le A_{i-1} (a_i - 1)$. 이를 반복적으로 적용하면 $B = next(A)$가 되므로 모순.

위와 같이 목걸이를 놓치지 않는 연산자 $next$가 있다면, 사전순으로 모든 목걸이를 빠지지 않게 세는 다음과 같은 간단한 알고리즘을 생각할 수 있다.

목록의 첫 문자열은 물론 사전순으로 최소인 목걸이 $1^N$이다.
목록에 마지막으로 쓴 문자열이 다시 목걸이가 될 때까지 반복적으로 $next$ 연산자를 적용시킨다.
2번의 결과로 나온 수를 목록에 적고 다시 2번 과정을 반복한다. 사전순으로 최대인 목걸이 $K^N$이 등장하면, 2번 과정을 멈춘다.

또는 위의 정리들에서 여러 가지 ‘도구’를 활용할 수 있다. 정리 1에 의해(조금 확장하면), 목걸이 $A_i = A_{i-1} a_i$에 대해 $a_i$를 임의의 $x > a_i$로 바꾸어도 목걸이가 된다. 정리 2에 의해 목걸이 $A_i = a_1 \cdots a_i$로 시작하는 가장 작은 목걸이는 $A_i$를 반복한 것이다. 다른 말로는, $A_i$가 목걸이라면, $A_i$를 얼마든지 반복해도(임의의 $l$에 대해 $(A_i)^\infty_l$) 목걸이가 된다는 것이다. 강력한 assertion들로, 아래와 같이 강력하게 목걸이를 생성하는 알고리즘을 만들 수 있다.

DFS를 재귀적으로 수행한다. 깊이가 $d$인 DFS 함수에서는 길이 $d$인 문자열 $S = A^\infty _d$를 전달받는다. 그리고,
1. 주기를 그대로 $A$로 유지하고 길이를 하나 늘인 문자열 $A^\infty_{d+1}$를 한 번 전달한다.
2. S의 끝에 글자를 하나 추가한 길이 $d+1$의 문자열들 중 1.에서 전달한 것보다 사전순으로 큰 것들을 전달한다. 이들의 주기는 문자열 전체이다.
DFS 함수가 깊이 $N$에 도달하면, i) 주기 $A$의 길이가 $N$의 약수이면, 목록에 추가한다. ii) 주기 $A$의 길이가 $N$의 약수가 아니면, 무시한다(같은 문자열이 $d=N$으로 들어올 것이다)

주목할 점은, 위 알고리즘은 목걸이가 아닌 문자열은 만들어내지 않는다. 게다가 위 알고리즘은 모든 목걸이를 만들어낸다!

정의 2. 문자열 $S$에 대해, $S$가 다른 문자열 $T$를 $k>1$번 반복해서 얻어지면, $S$가 주기적이라고 말한다. 그리고 이 때, $k$를 최대화하는 $T$를 $S$의 주기라고 하고, $\bar{S}$로 표기한다. 그러한 $T$와 $k$가 존재하지 않으면 $S$가 비주기적이라고 말한다.

정의 3. 비주기적인 목걸이를 Lyndon 단어라고 한다.

위 두 정의에서, 모든 길이 $N$인 목걸이에는 길이가 $N$의 약수인 Lyndon 단어가 하나씩 대응됨을 확인할 수 있다. 비주기적 목걸이일 경우에는 그 자체를, 주기적 목걸이일 경우에는 이의 주기를 취하면 Lyndon 단어를 하나씩 만들 수 있기 때문이다. 이로부터 길이 $N$인 모든 문자열이 한 번씩 등장하는 de Bruijn 수열을 만들어내는 간단하지만 일견 비직관적인 알고리즘을 만들 수 있다.

길이가 $N$의 약수인 Lyndon 단어를 사전순으로 모두 모아 이어붙인다.

믿기지 않는가? 예시로 확인해 보자. N=4, K=3일 때 위 알고리즘은 다음과 같이 de Bruijn 수열을 만들어낸다. 쉼표는 각각의 Lyndon 단어를 구분하기 위해 적었다.

1, 1112, 1113, 1122, 1123, 1132, 1133, 12, 1213, 1222, 1223, 1232, 1233, 13, 1322, 1323, 1332, 1333, 2, 2223, 2233, 23, 2333, 3

증명. 먼저, 위 알고리즘이 만드는 문자열의 길이는 $K^N$이다. 왜냐하면 길이가 $l$인 Lyndon 단어 하나는 이 단어의 cyclic shift $l$개에 대응되고, 이들 각각은 길이 $N$의 목걸이의 cyclic shift에, 즉 임의의 문자열 하나에 대응되므로, 만들 수 있는 각각의 길이 $N$ 문자열을 위 문자열의 문자 하나에 대응할 수 있게 된다. (즉, 문자열들은 주기의 cyclic shift에 대해 equivalence class를 이루기 때문이다) 따라서, 위 문자열의 길이는 만들 수 있는 문자열의 개수와 같은 $K^N$.

우리가 만든 문자열 $B$에 길이 $N$의 모든 문자열이 한 번씩 등장함을 보일 것이다. 모든 문자열은 목걸이의 cyclic shift이므로, 임의의 목걸이 $A$의 모든 cyclic shift가 등장함을 보일 것이다.

$A = A_k K^{N-k}$ ($a_k < K$)로 두자. (1) 이들의 cyclic shift들 중 먼저 $cyc_i (A) = K^i A_k K^{N-k-i}$ 꼴이 될 때, 즉 $1 \le i \le N-k$일 때 등장함을 보인다. $X_0 = A_k K^{N-k-i}$로 시작하는 사전순으로 가장 빠른 Lyndon 단어를 $X$라 하자. $X_0$은 물론 목걸이이고, $next$ 연산을 몇 번 적용시켜 $X_0$이 되는(즉, 사전 순으로 $X_0$ 바로 이전의) 길이 $N-i$의 목걸이 $Y_0$이 존재한다. $Y = Y_0 K^i$는 ($Y_0$로 시작하는 마지막) 목걸이가 되고, $Y_0 < X_0$이므로 $\bar{Y}$는 $K^i$로 끝난다. $X$는 $Y$ 바로 다음 등장하는 목걸이가 되므로, $B$에는 $\bar{Y}X$가, 특히는 $K^i a_1 \cdots a_k K^{N-k-i}$가 부분문자열로 등장한다.

(2) 그리고 나머지 $N-k < i \le N$인 경우를 생각하자. (2-1) 이 때 $cyc_i (A) = a_{N-i+1} \cdots a_k K^{N-k} A_{N-i}$이다. 만약 $A$가 주기적이라면, Lyndon word $\bar{A} = A_{k’} K^{l-k’}$ ($l-k’ = N-k$)로 뒀을 때 다음 목걸이 $\bar{A}’ = A_{k’-1} (a_{k’}+1) a_{k+1}’ \cdots a_l ‘ $에 대해, $A$ 다음의 목걸이는 $A’ = \bar{A}^{\frac{N}{l}-1} \bar{A}’$이 된다. $A’$는 비주기적이고, 따라서 $\bar{A}A’$는 $\bar{A}^{\frac{N}{l}} A_{k’-1} = A A_{k’-1}$을 포함하게 되고, 따라서 $N-k < i \le N$인 모든 $cyc_i(A)$를 포함하게 된다. ($\bar{A}$의 다음 목걸이가 존재하지 않을 때, 즉 $\bar{A} = ‘Z’$인 경우에는 자명하다)

(2-2) $A$가 비주기적일 때에는, $A$의 다음 목걸이 $A’ = a_{k-1} (A_k+1) X$를 생각한다. $A’$가 비주기적일 때는 $AA’$가 $cyc_i(A)$를 포함한다. $A’$가 주기적일 때에는, 다음 목걸이가 $A’‘$일 때 위 문단의 논의에 따라 $A’A’‘$가 $A’$를 포함한다.

따라서 $A$의 모든 cyclic shift는 단 한 번만 등장하고, 따라서 우리는 올바른 de Bruijn 수열을 만들었다.

위 알고리즘은 더욱이, 사전순으로 가장 작은 de Bruijn 수열을 만들어낸다. 위에서 설명한 모든 목걸이를 만드는 알고리즘을 응용하면 모든 목걸이의 주기를 만들 수 있고, 따라서 이는 de Bruijn 수열을 만드는 알고리즘이 된다. 이론이 이해하기 힘든 데에 비해 코드로의 구현은 짧고 간단한 것을 볼 수 있다.

    int rec[MAXN];
    vector<int> de_bruijn(int K, int N) {
    	vector<int> res;
    	function<void(int, int)> dfs = [&](int x, int p) {
    		if (x == N) {
    			if (N%p == 0) for (int i=0; i<p; i++) res.push_back(rec[i]);
    		} else {
    			int k = (x-p >= 0) ? rec[x-p] : 1;
    			rec[x] = k;
    			dfs(x+1, p);
    			for (int i=k+1; i<=K; i++) {
    				rec[x] = i;
    				dfs(x+1, x+1);
    			}
    		}
    	};
    	dfs(0, 1);
    	return res;
    }

2018 ICPC Asia Jakarta Regional의 Smart Thief (https://www.acmicpc.net/problem/16575) 문제를 de Bruijn Sequence를 이용하여 풀 수 있다. 문제의 정해는 위 de Bruijn 그래프를 이용한 $O(kL)$ 알고리즘을 의도하였다. 그리고 $N$이 예를 들면 $40$ 이상일 때에는 그냥 아무 수열이나 찍어도 중복된 부분수열이 있을 확률이 극도로 낮다는 점을 이용해, 아무 수열이나 찍는 것이 출제자가 의도한 풀이이다. 하지만 위의 길이당 $O(1)$ de Bruijn 수열 생성 알고리즘을 사용한다면, 문제를 매우 쉽게 해결할 수 있게 된다.

참고문헌

https://en.wikipedia.org/wiki/De_Bruijn_sequence
H. Fredricksen and J. Maiorana, Necklaces of beads in k colors and k-ary de Bruijn sequences, Descrete Mathematics, 23 (1978) 207-210.
Eduardo Moreno, On the theorem of Fredricksen and Maiorana about de Bruijn sequences, Advances in Applied Mathematics 33 (2004) 413-415.

De Bruijn 수열

De Bruijn 수열

De Bruijn 그래프

더 빠른 알고리즘

참고문헌

Android Studio를 이용한 앱 UI 2

How to build WebAssembly app with Rust