Maximum Matching in General Graph
Maximum matching algorithm of “General graph”
그래프에서 matching은 인접해있는 정점쌍을 중복되지 않게 선택한 것들의 집합이며, maximum matching은 이 집합 중 가장 크기가 큰 것을 구하는 문제이다. 이와 관련하여 만약 그래프가 bipartite라면 보다 간편하게 풀 수 있으며, 이 알고리즘은 잘 알려져있다. 하지만 일반적인 그래프에서 찾는 알고리즘은 보다 복잡하여 CP에서 잘 다루지 않는 내용이다. 그래서 이번에는 잘 알려지지 않은 그래프 최대 매칭에 대한 알고리즘을 소개해보려 한다.
여기서는 일반적인 그래프에서 최대 매칭을 구하는 알고리즘 중 Blossom algorithm에 대해 소개해보려 한다. 이 알고리즘에 대해 알아보기 앞서, 필요한 개념을 몇가지 정리해보도록 하자.
Prelimirary
어떤 그래프 $G=(V,E)$ 가 주어져 있고, 이 그래프에서 찾은 어떤 매칭을 $M$ 이라 하자. 여기서 $M$ 내의 어떠한 간선들에도 인접하지 않은 정점 $v$를 exposed vertex라 하자. 그리고 임의의 path $P$ 에 에 속한 간선들이 반복적으로 $M$에 속하거나 속하지 않는 것을 반복한다면 이 path $P$를 alternating path라고 한다.
이를 이용하여 argumenting path를 정의해보자. $Definition.$ 어떤 alternating path $P$의 양 끝점이 exposed vertex이면 이 path를 argumenting path라 한다.
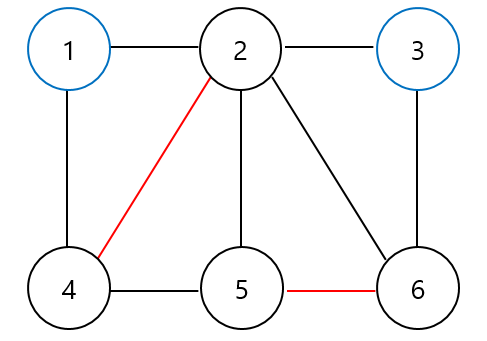
위의 그림을 예시로 설명하자면, 빨간 간선을 $M$에 속한 간선이라 할 때 파란 정점이 exposed vertex이며 $(2, 4, 5), (1, 4, 2, 3), (3, 6, 5, 2)$와 같은 path를 alternating path라 한다. 여기서 argumenting path는 $(1,4,2,5,6,3),(1,2,4,5,6,3)$이다.
이런 argumenting path들은 $M$에 속하지 않은 간선의 수가 $M$에 속한 간선의 수보다 하나 더 많다는 특징이 있다. 이를 이용하여, 어떤 한 argumenting path에서 $M$에 속하지 않은 간선들을 $M$에 추가하고, 이미 속해있던 간선들을 뺸 후 만든 새로운 매칭 $M’$을 만들었을 때, 이는 여전히 매칭의 조건을 만족할까? 양 끝점을 제외한 정점의 차수는 변하지 않으며, 양 끝점은 차수가 1증가하지만 원래 exposed vertex였기 때문에 새롭게 만든 그래프 또한 매칭이다. 그리고 이 프로세스를 진행한 후 $|M’|$은 $|M|$보다 1증가한다는 특징이 있다. 이 특징을 고려하여 우리는 다음과 같은 생각을 해볼 수 있다. 만약 위의 과정을 가능한 반복한다면, 그 결과는 과연 maximum matching이 되는가?
Berge’s lemma는 이 그래프에 argumenting path가 더 이상 없다면, 그 때 $M$은 최대라는 것을 보여주고, 그 역도 성립합을 보여준다. (이에 대한 자세한 증명은 생략한다.) 이 lemma에 의해 우리는 주어진 매칭 $M$을 두 케이스로 분류할 수 있다.
- $M$은 maximum matching이다.
- 그래프에 argumenting path가 있다.
따라서 항상 argumenting path를 찾고, 이를 변환해주는 알고리즘을 완성하면 우리의 목표인 그래프에서의 최대 매칭 $M$을 찾을 수 있다. 그러면, 이런 argumenting path를 어떤 방법으로 찾아야 하는가?
Algorithm
Finding Blossom
Blossom algorithm에서 blossom은 무엇인가? 이 알고리즘에서 blossom을 다음과 같이 정의한다. $Definition.$ 주어진 그래프에서 blossom $B$는 $2k+1$개의 간선으로 이루어진 사이클이며, 이 사이클에서 정확히 $k$개의 간선은 $M$에 속해야 하고 이 중 하나의 정점에서 시작하여 exposed vertex로 끝나는 짝수 길이의 alternating path가 존재해야 한다.
임의의 blossom을 찾기 위해선 다음과 같은 알고리즘을 수행하면 된다.
- 임의의 exposed vertex를 시작으로 two coloring을 시작한다. 정점의 색을 0,1이라 할 때 시작 정점의 color는 0으로 한다.
- 0으로 색칠된 정점에 인접한 간선들에 대해 해당 간선이 매칭에 포함되있지 않다면 다음의 과정을 진행한다.
- 현재 0으로 색칠된 정점을 $u$, 선택한 간선의 다른 끝점을 $v$라 하자. 만약 $v$가 색칠되어있지 않으며, exposed vertex라면 생략하고 다른 정점을 고려해본다.. (maximum matching을 찾는 알고리즘에서는 이를 이용하여 일련의 과정을 거쳐 argumenting path를 찾고 매칭의 크기를 늘리지만, 현재 우리는 blossom을 찾는 알고리즘을 보고 있기 때문에 이를 잠시 생략한다. 이를 처리하는 방법은 추후 최대 매칭 알고리즘을 설명할 때 기술할 것이다.)
- $v$가 색칠되어있지 않다면 $v$를 1로, $v$와 매칭된 정점 $x$를 0으로 색칠하고 $x$에서 이 알고리즘을 다시 수행한다.
- 만약 색칠되어 있다면 $v$의 색이 0인지 확인한다. 만약 0이라면 $(u, v)$ 간선과 $v\rightarrow u$ 에서 사용한 간선들을 모아 사이클을 만든다. 해당 cycle이 blossom가 된다.
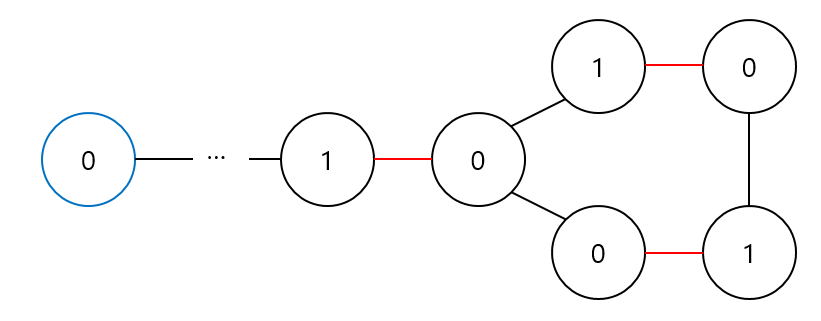 [blossom의 예 여기서 빨간 간선은 매칭이 속하는 간선이며 파란 정점은 exposed vertex이다.]
[blossom의 예 여기서 빨간 간선은 매칭이 속하는 간선이며 파란 정점은 exposed vertex이다.]
알고리즘은 그래프 탐색 알고리즘 하나로 구현할 수 있을 만큼 간단하다. 그러면 해당 알고리즘이 정말 blossom을 찾는가? 이를 간단히 증명해보면, 우선 사이클의 길이는 홀수임이 분명하다. 또한 exposed vertex에서 2-3과정에서 찾은 $v$정점 사이의 거리는 두 정점 모두 같은 색이기 때문에 짝수임을 보장할 수 있다. 따라서 해당 사이클은 blossom이 된다.
Algorithm
Blossom은 찾았는데 이와 maximum matching은 어떤 관계가 있는가? 우리는 다음 theorem은 blossom을 이용하여 어떤 식으로 maximum matching을 구할지 알려준다.
$Theorem. $ 그래프에서 찾은 blossom을 $B$라 하자. 이 $B$를 하나의 정점으로 압축한 새로운 그래프를 $G’$이라 하고 이에 파생된 새로운 매칭을 $M’$이라 하자. 이때, 만약 $G’$이 $M’$을 이용하여 argumenting path를 구할 수 있다면 $G$에서도 $M$을 이용하여 argumenting path를 구할 수 있으며 이 역도 성립한다.
증명도 간략하게 해보자. 우선 압축된 blossom을 $v_b$라 하자. 이떄 $G’$의 argumenting path가
- Case 1. $u\rightarrow v$, 문제없이 해결할 수 있다.
- Case 2. $u\rightarrow … \rightarrow u’\rightarrow v_b\rightarrow v’ \rightarrow … \rightarrow v$, 여기서 $u’\rightarrow v_b$ 가 매칭에 속할 때, $G$에서 u를 exposed vertex로 하는 blossom을 구할 수 있으며, $u’\rightarrow v_b$ 간선을 제외하고 임의의 정점 $x\in B$와 $y\notin B$ 사이의 간선 $(x, y)$는 매칭이 아님을 보장할 수 있기에 $v_b\rightarrow v’$는 항상 매칭에 속하지 않은 간선이 된다. 그리고 $v_b$를 풀어 $w_1,w_2,…,w_t$ 간선을 만들 떄, $w_1 \rightarrow w_t$ 경로는 두 가지가 있기 때문에 둘 중 적절한 경로를 선택하여 alternating path를 완성할 수 있다. $v_b\rightarrow v’$ 간선이 매칭에 속할떄도 위와 같이 $G$에서 argumenting path를 완성할 수 있다.
- Case 3. $u \rightarrow … \rightarrow u’ \rightarrow v_b$, 위에서 기술한 알고리즘을 따라 $B$를 만들었을 떄 이런 상황이 나오려면 $G$ 그래프에서 $B$ 내부에 exposed vertex가 있어야 한다. 그렇지 않다면 $v_b$에 매칭된 정점이 하나 있어야 하며 따라서 $v_b$가 $G’$ 그래프에서 exposed edge가 될 수 없기 때문이다. 이 정보를 이용하여, Case 2와 비슷하게 $G$에서 그래프를 복원할 수 있다.
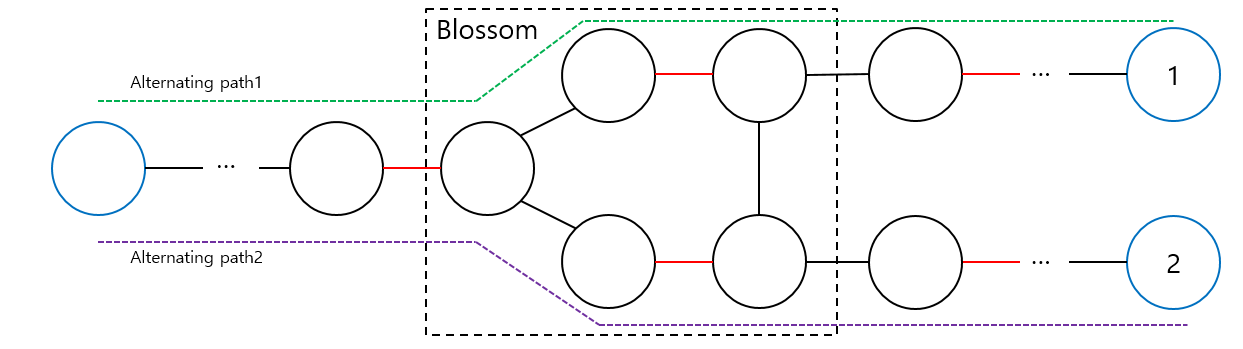 [Case 2에 대한 예제. Blossom이 위와 같이 형성되었을 때 이를 포함하는 argumenting path들은 위와 같은 형태일 수 밖에 없으며, 이때 1번과 같은 exposed vertex가 선택된 경우 path1, 2번의 경우 2번 path와 같이 argumenting path를 구성할 수 있다.]
[Case 2에 대한 예제. Blossom이 위와 같이 형성되었을 때 이를 포함하는 argumenting path들은 위와 같은 형태일 수 밖에 없으며, 이때 1번과 같은 exposed vertex가 선택된 경우 path1, 2번의 경우 2번 path와 같이 argumenting path를 구성할 수 있다.]
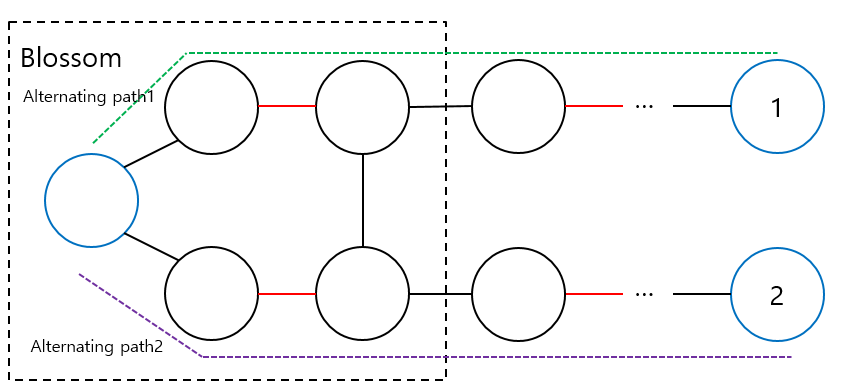 [Case 3에 대한 예제. argumenting path가 3번 예제에 나타난 것처럼 구성된다면 blossom에는 반드시 exposed vertex가 포함되어야 한다. 이를 이용하여 Case 2와 유사하게 argumenting path를 구성할 수 있다.]
[Case 3에 대한 예제. argumenting path가 3번 예제에 나타난 것처럼 구성된다면 blossom에는 반드시 exposed vertex가 포함되어야 한다. 이를 이용하여 Case 2와 유사하게 argumenting path를 구성할 수 있다.]
$G$에서 $G’$의 argumenting path를 구성하는 방법은 위와 비슷하게 보일 수 있으니 생략하도록 하겠다.
이제 이 알고리즘을 코드로 옮기는 일만 남았다.
Implementation
위의 알고리즘은 결과적으로 두 exposed vertex를 찾아 이들 사이에서 만들어지는 argumenting path를 찾고 이들을 flip하는 것이다. 이를 잘 기억하고, 각 exposed vertex에 대해 이와 연결될 수 있는 다른 exposed vertex를 찾아보자.
구현방법을 간단하게 설명하면 하나의 exposed vertex에서 트리를 만들어가며 다른 exposed vertex를 찾아 그 argumenting path를 이용하여 매칭을 1 증가시키는 것이다.
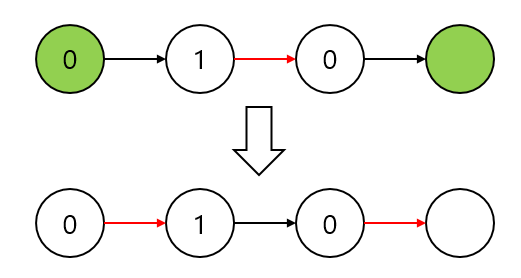
위 그림에서 빨간 간선은 매칭에 포함된 간선, 초록 정점은 exposed vertex이다. 위와 같이 coloring과정에서 두 exposed vertex를 찾았을 경우 그 경로를 역추적하며 매칭을 바꿔준다.
그러면 만약 중간에 Blossom을 찾으면 이를 어떤 식으로 압축해야 하는가?
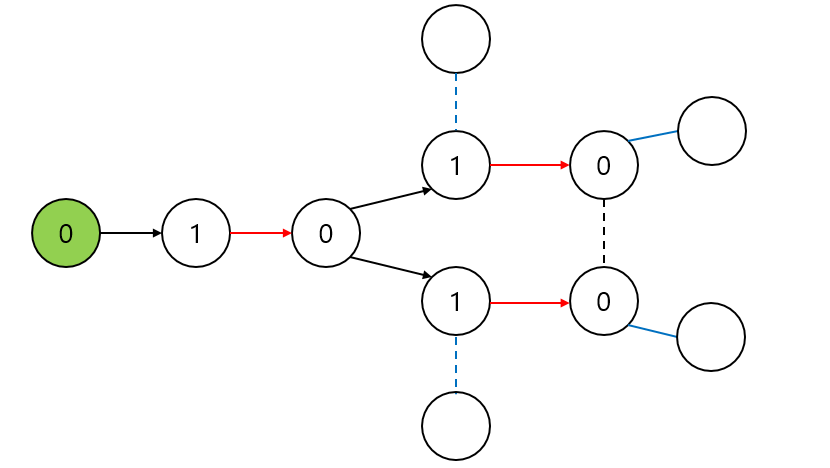
위 그림과 같은 상황을 가정해보자. 여기서 검은 점선이 현재 보고있는 간선, 파란 실선은 이후 보아야할 간선, 그리고 파란 점선은 1번으로 색칠된 정점과 연결된 간선들이기 때문에 탐색에 쓰이지 않는 간선들이다. 여기서 검은 간선을 연결하면 하나의 Blossom을 찾은 것이다.
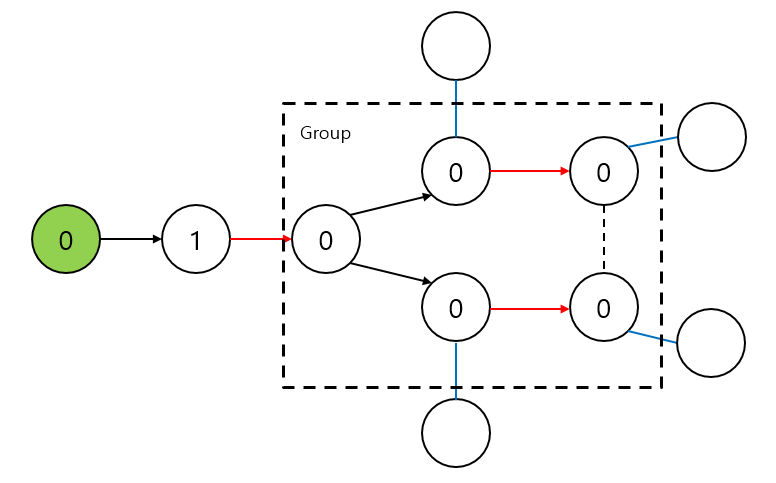
Blossom에 해당하는 부분을 하나의 group이라고 표기해둔다. (여기서 group을 하는 이유는 이미 같은 그룹으로 묶인 한 Blossom내의 두 정점을 보고 다시 grouping을 하는 일이 없도록 하기 위해서이다.) Blossom을 찾았을 때 압축을 한다고 생각해보면, 결과적으로 압축된 정점은 기존의 exposed vertex에서 보았을 때 0으로 색칠되어 있어야 한다. 따라서 한 Blossom내의 1로 색칠된 정점들의 색을 0으로 바꾼 후 이들과 인접한 간선들도 탐색에 쓴다.

두 개의 Blossom도 단순하게 그룹화를 통해 합치면 된다. 위의 그림을 예로, 파란 점선이 지금 고려하고 있는 간선이라면 두 그룹을 합쳐 새로운 그룹으로 만들어준다.
이제 트리를 형성하면서 Blossom을 압축(그룹화)할 수 있다. 그러면 이제 어떤 argumenting path를 찾은 후 이를 복원하는 방법에 대해 살펴보자.
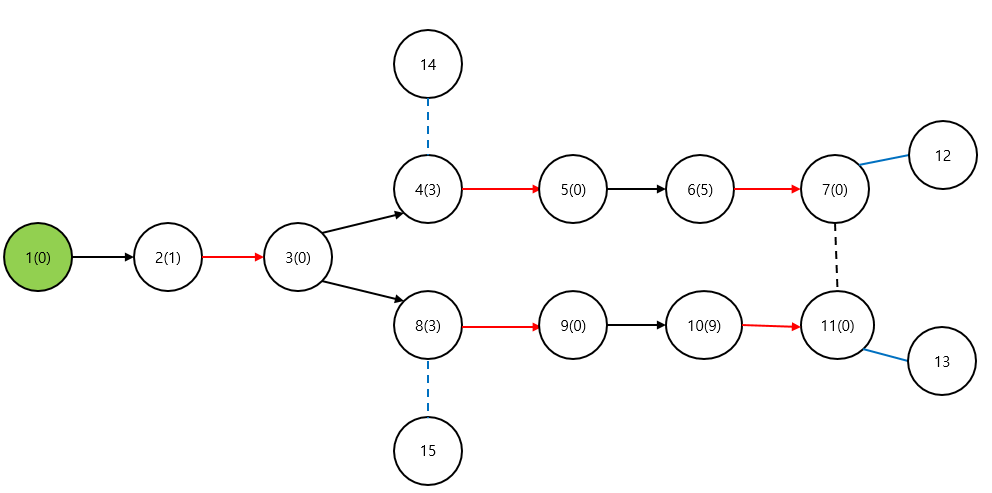
위에서 사용한 예제로 잠시 돌아가보자. 각 노드에 적힌 숫자는 <노드번호(부모노드의 번호)>를 의미한다. (여기서 부모의 번호가 0인 경우는 아직 부모가 정해지지 않은 경우로 한다.) 위의 예제에서 만약 12, 13번 노드, 이와 인접한 노드들을 탐색하는 과정에서 exposed vertex를 찾았다면 이미 구성된 트리의 경로를 역추적하여 argumenting path를 복원할 수 있다. 그런데 만약 14번 혹은 15번 노드, 이와 인접한 노드들을 탐색했을 때 exposed path를 찾으면 어떤 식으로 복원을 해야 할까? 만약 14번 노드에서 exposed vertex를 찾았다면 (…, 14, 4, 5, 6, 7, 10,…)의 경로를 복원해야 하며, 15번 노드에서 exposed vertex를 찾았다면 (…, 15, 8, 9, 10, 11, 7,…)의 경로를 복원해야 한다. 이를 위해 그룹화 과정에서 조금 특이하게 부모노드의 번호를 배정해준다.
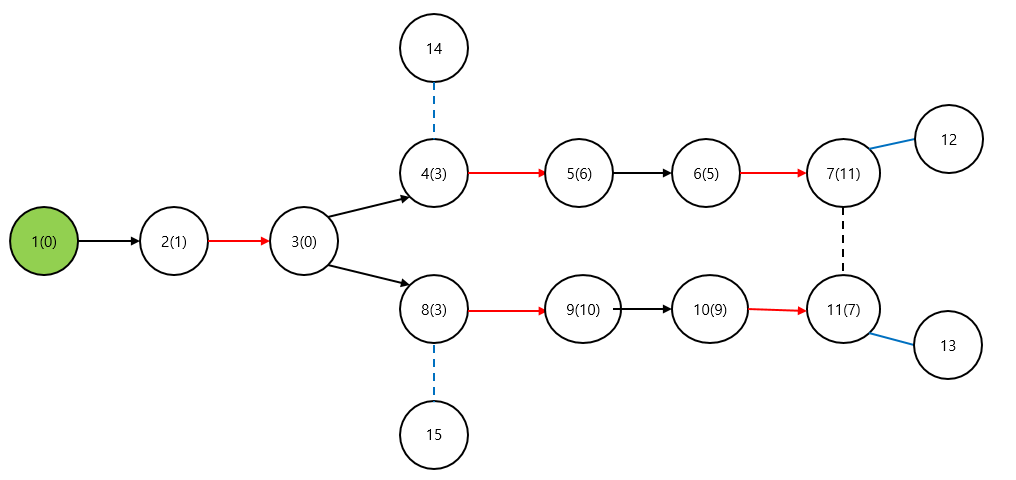
5, 7, 9, 11번 노드의 부모번호를 잘 살펴보자. 지금 보고있는 간선을 중심으로 트리를 역으로 올라가며 부모를 매겨주고, 7, 11번 노드는 서로를 부모로 준다. 이런식으로 배정한 후, argumenting path 복원을 할 때 (현재 노드의 부모, 그 노드와 매칭된 노드)를 한 쌍으로 가져가며 경로를 복원해주면 위에서 언급한 문제가 발생하지 않고 적절한 argumenting path를 찾을 수 있다.
Code
const int MAX = 501;
int mat[MAX], par[MAX], grp[MAX], col[MAX], vis[MAX], n, m;
vector<int> adj[MAX];
int lca(int root, int u, int v) {
int chk[MAX] = {0, };
while(u != root) {
chk[u] = 1;
u = grp[par[mat[u]]];
}
while(v != root) {
if(chk[v]) return v;
v = grp[par[mat[v]]];
}
return root;
}
void group_blossom(int p, int u, int v) {
while(grp[u]!=p) {
int nv=mat[u], nu=par[nv];
if(!vis[nv]) {
vis[nv] = 1;
}
par[u] = v;
grp[u] = grp[nv] = p;
u = nu;
v = nv;
}
}
void flip_argument(int root, int u) {
while(par[u] != root) {
int v = par[u], w = mat[v];
mat[u] = v; mat[v] = u;
mat[w] = 0;
u = w;
}
mat[u] = root; mat[root] = u;
}
int find_argument(int r) {
fill(par, par+n+1, 0);
fill(col, col+n+1, -1);
fill(vis, vis+n+1, 0);
for(int i=1;i<=n;i++) grp[i] = i;
queue<int> que;
que.push(r);
col[r] = 0;
vis[r] = 1;
while(!que.empty()) {
int u=que.front();
que.pop();
for(auto &v:adj[u]) {
if(col[v] == -1) {
par[v] = u;
col[v] = 1;
if(!mat[v]) {
flip_argument(r, v);
return 1;
}
col[mat[v]] = 0;
vis[mat[v]] = 1;
que.push(mat[v]);
} else if(col[v]==0 && grp[u]!=grp[v]) {
int p=lca(grp[r], grp[u], grp[v]);
group_blossom(p, u, v);
group_blossom(p, v, u);
for(int i=1;i<=n;i++) if(vis[i] && col[i]) {
col[i] = 0;
que.push(i);
}
}
}
}
return 0;
}
int match() {
int ret=0;
fill(mat, mat+n+1, 0);
for(int i=1; i<=n; i++) if(!mat[i]) {
if(find_argument(i)) ret++;
}
return ret;
}
마치며
이를 테스트할 수 있는 문제들은 아래에 있다.
그래프 최대매칭 알고리즘은 복잡하지만 이를 이해하기 어렵진 않다. PS에서 볼 일은 많이 없겠지만, 그래도 어떤식으로 알고리즘을 구성하는지 알고있다면 아마 도움이 될 수 있지 않을까 싶다.