STL set을 이용한 Convex Hull Trick 구현
소개
Convex Hull Trick은 여러 일차 함수들의 최댓값이나 최솟값을 찾고자 할 때 유용하게 쓰이는 테크닉입니다. 이미 많은 대회에 출제된 바 있어 최근에는 대회를 준비한다면 필수적으로 알아야 할 테크닉이기도 합니다. 혹시 이 기법에 대해 잘 모른다면 구글 등에 검색하셔서 공부하시는 것을 추천드립니다. 잘 설명된 글들이 많기 때문에 여기서는 기법에 대한 자세한 내용까지는 다루지 않을 것입니다.
주어지는 일차 함수들의 기울기가 증가하거나 감소한다면 스택 자료구조 하나만으로 간단하게 Convex Hull Trick을 구현할 수 있습니다. 만약 그렇지 않고 기울기가 들쑥날쑥한다면 잘 알려진 방법으로는 세그먼트 트리를 사용하거나, Li-Chao tree를 사용하는 방법이 있습니다.
이에 비해 잘 쓰는 방법은 아니지만 STL set을 이용해서 구현하는 방법도 있습니다. 구현이 약간 번거로울 수는 있지만, 알고리즘 자체는 매우 직관적이고 단순합니다. 따라서 이 글에서는 STL set을 이용해서 Convex Hull Trick을 구현하는 방법에 대해 소개하고, 그 코드를 공유하고자 합니다.
Convex Hull Trick은 1) 새로운 직선을 추가하는 연산과, 2) 특정 $x$좌표에 대응되는 직선을 찾는 연산으로 구성됩니다. 먼저 1에 해당하는 직선 추가 연산을 어떻게 구현하는지 알아보겠습니다.
직선 추가
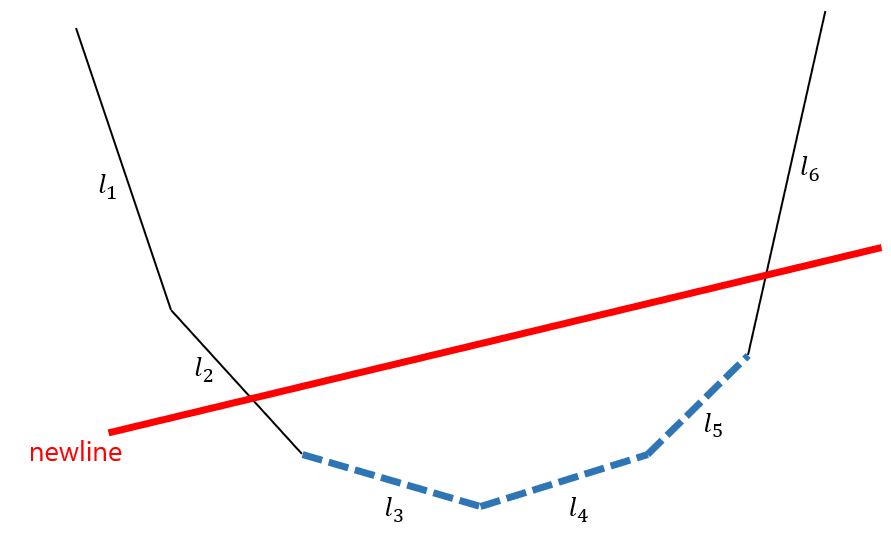
현재 Convex Hull의 모양이 다음 그림과 같고, 빨간 직선 하나를 추가하는 상황을 가정해봅시다. 최댓값을 나타내는 Convex Hull이라고 가정하겠습니다. 그러면 빨간 직선 아래의 파란 직선들은 더 이상 최댓값이 될 수 없으므로 제거해주어야 합니다.
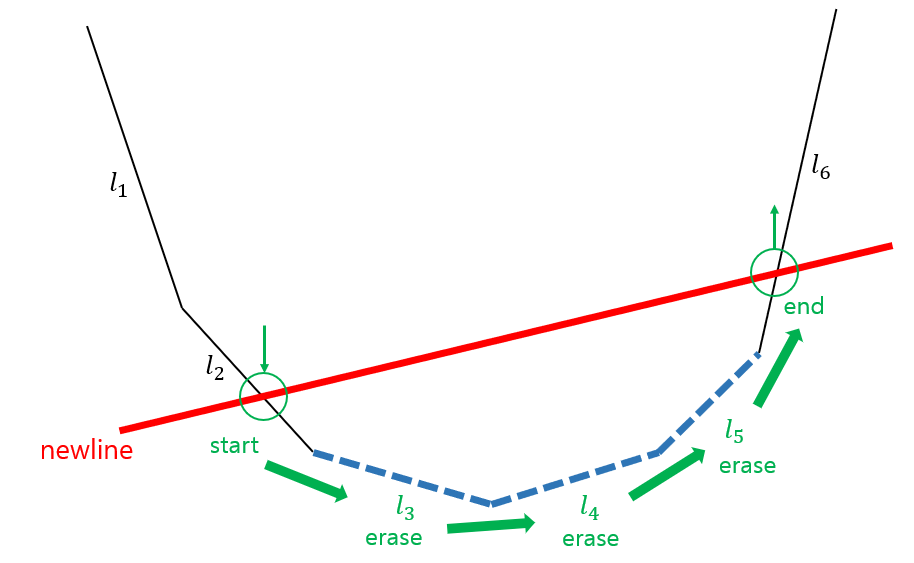
이때 파란 직선들은 빨간 직선과 Convex Hull이 만나는 두 지점 사이에 존재하고, Hull 상에서 연속한 위치에 놓여있음을 알 수 있습니다. 따라서 빨간 직선과 Convex Hull이 만나는 지점을 찾아 한 방향으로 이동하면서 모든 파란 직선들을 제거하는 방법을 생각해볼 수 있습니다. 즉, 아래 그림처럼 $l_2$에서 시작하여 $l_6$까지 이동하며 $l_3, l_4$를 제거하는 것입니다.
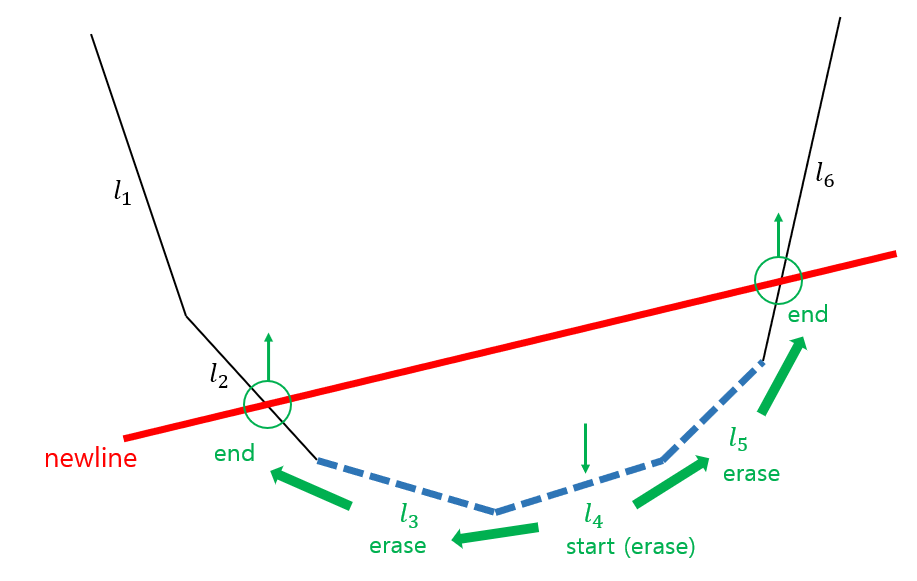
하지만 Convex Hull과 만나는 지점을 빠르게 찾는 것은 생각보다 어렵습니다. 여기서 접근을 약간 달리하여 양 끝이 아닌 중간 어딘가에 위치한 직선 하나로부터 양방향으로 이동하며 직선들을 제거하는 방법을 생각해봅시다. 아래 그림에서는 $l_4$에서 시작하는 경우를 예시로 나타내었습니다.
중간 직선을 찾는 가장 단순한 방법은 기울기를 이용하는 것입니다. 빨간 직선과 만나는 Convex Hull 상의 두 직선의 기울기 중 작은 것을 $m$($l_2$의 기울기), 큰 것을 $M$($l_6$의 기울기)이라 하면 기울기가 $m$보다 크고 $M$보다 작은 모든 직선들은 제거 대상이 됨을 알 수 있습니다. 따라서 기울기가 $[m, M]$ 범위에 속하는 직선을 아무거나 하나 찾으면 됩니다.
여기서 빨간 직선의 기울기를 이용해봅시다. 빨간 직선의 기울기를 $a$라 하면 $m<a<M$을 만족합니다. 이때 Convex Hull 상에서 기울기가 $a$의 lower bound($a_l$)인 직선을 찾으면 $m<a\leq a_l\leq M$을 만족하므로, 이 직선은 제거 대상이 되거나($a_l<M$) 빨간 직선과 만나거나($a_l=M$) 반드시 둘 중 하나의 경우에 해당함을 알 수 있습니다. 따라서 이 직선을 시작으로 양 옆으로 이동하면서 제거 여부를 판단하여 모든 파란 직선들을 제거해주면 됩니다. 마지막으로 빨간 직선을 자료구조상 적절한 위치에 삽입해줍니다.
이러한 과정들은 빠른 insert/erase 연산, lower_bound 연산만을 요구하므로 STL set 만으로 구현할 수 있습니다. 자세한 구현 내용은 아래에서 다시 다루겠습니다.
쿼리 연산
이번에는 특정 $x$좌표에 대응되는 직선을 찾는 쿼리 연산에 대해 알아보겠습니다. 쿼리 연산을 구현하려면 Convex Hull에서 인접한 두 직선의 교점들에 대한 정보를 계속 관리해주어야 합니다. 이를 위해 별도의 set을 하나 더 만들고 직선이 추가되거나 제거될 때마다 교점 정보를 업데이트하는 방식으로 관리해줍니다. 그 후 쿼리 요청이 들어오면 $x$좌표와 가까운 교점을 lower bound 연산 등으로 찾고, 이에 대응하는 직선을 리턴하도록 합니다.
여기까지가 알고리즘의 전부입니다. 이제 약간 번거로운 구현에 대해 살펴보겠습니다.
구현
구현을 단순하게 하기 위해 직선의 기울기와 $y$절편 값, 그리고 쿼리로 들어오는 $x$좌표가 모두 정수라고 가정하겠습니다.
우선 직선들을 저장하는 line_set과 교점들을 저장하는 point_set을 각각 만들어줍니다. 직선은 (기울기, $y$절편) 쌍을 저장하고 교점은 (교점의 $x$좌표, 교점의 오른쪽에 위치한 직선) 쌍을 저장할 것입니다.
using ll=__int128;
using Line=pair<ll,ll>;
using Point=pair<ll,Line>;
set<Line> line_set;
set<Point> point_set;
이제 직선 추가 연산을 구현해봅시다. 직선을 추가하기 전에 앞서 설명한 것처럼 직선의 lower bound를 찾고 양방향으로 이동하면서 기존 직선들의 제거 여부를 판단할 것입니다. 제거 여부는 bad라는 함수로 판단하는데, bad(a, b, c)는 직선 a, b, c가 Convex Hull 상에서 a < b < c 순으로 존재할 수 있는지 확인합니다. 즉, (a와 b의 교점) < (b와 c의 교점) 이라면 가능하므로 false를 (not bad), 그렇지 않으면 true를 반환합니다.
오른쪽으로 이동하는 경우에는 bad(새로운 직선, 현재 직선, 다음 직선)을 체크하고 왼쪽으로 이동하는 경우에는 bad(다음 직선, 현재 직선, 새로운 직선)을 체크하여 현재 직선의 제거 여부를 판단합니다.
두 직선의 교점을 구할 때에는 getf(a, b)라는 함수를 사용했습니다. 일반적으로 교점의 좌표는 정수가 아닐 수 있지만, 앞서 쿼리로 들어오는 $x$좌표가 정수라고 가정했기 때문에 내림한 값을 대신 사용해도 됩니다. 쿼리의 $x$좌표가 유리수이거나 실수인 경우에는 추가적인 로직을 구현해주어야 하기 때문에 조금 복잡합니다. 해당 경우의 구현체는 아래에 따로 링크를 걸어놓겠습니다.
inline Point getf(Line a,Line b) {
if(b.fi>a.fi) return {(a.se-b.se)/(b.fi-a.fi)-((a.se-b.se)%(b.fi-a.fi)<0),b};
return {(b.se-a.se)/(a.fi-b.fi)-((b.se-a.se)%(a.fi-b.fi)<0),b};
}
inline bool bad(Line a,Line b,Line c) {
return getf(b,c)<=getf(a,b);
}
void insert(Line newline) {
auto it=line_set.lower_bound({newline.fi,-INF});
if(it!=line_set.end()&&it->fi==newline.fi) {
if(it->se<newline.se) it=_erase(it);
else return;
}
if(it!=line_set.end()&&it!=line_set.begin()&&bad(*prev(it,1),newline,*it))
return;
if(it!=line_set.begin()) {
auto jt=prev(it,1);
while(jt!=line_set.begin()&&bad(*prev(jt,1),*jt,newline)) {
jt=_erase(jt);
jt--;
}
}
while(it!=line_set.end()&&next(it,1)!=line_set.end()&&bad(newline,*it,*next(it,1)))
it=_erase(it);
_add(newline);
}
직선을 추가하거나 제거할 때에는 교점도 함께 업데이트해야 하므로 _add, _erase라는 로직을 구현해줍니다. _add의 경우를 예로 들면, 직선 a와 b 사이에 c라는 직선을 삽입하는 경우, 기존의 a와 b의 교점은 제거되고 a와 c의 교점, b와 c의 교점이 추가됩니다. 이는 getf로 교점을 구하고 set의 insert와 erase를 적절히 사용하여 구현하면 됩니다.
특히 point_set에는 항상 (-INF, 첫 번째 직선) 원소를 저장하여 왼쪽 구간을 커버해주어야 합니다.
void _add(Line ln) {
auto it=line_set.lower_bound(ln);
if(it!=line_set.end()) {
if(it==line_set.begin()) point_set.erase({-INF,*it});
else point_set.erase(getf(*prev(it,1),*it));
point_set.insert(getf(ln,*it));
}
if(it!=line_set.begin())
point_set.insert(getf(*prev(it,1),ln));
else point_set.insert({-INF,ln});
line_set.insert(ln);
}
set<Line>::iterator _erase(set<Line>::iterator it) {
if(it!=line_set.begin())
point_set.erase(getf(*prev(it,1),*it));
else point_set.erase({-INF,*it});
if(next(it,1)!=line_set.end()) {
point_set.erase(getf(*it,*next(it,1)));
if(it!=line_set.begin())
point_set.insert(getf(*prev(it,1),*next(it,1)));
}
return line_set.erase(it);
}
이제 쿼리 연산을 구현해봅시다. point_set에서 주어진 $x$좌표보다 작거나 같은 최대의 원소를 찾고, 이에 할당된 직선을 리턴하면 됩니다.
ll query(ll x) {
auto it=point_set.lower_bound({x,{-INF,-INF}});
if(it==point_set.begin()) return -INF;
it--;
return (it->se.fi)*x+(it->se.se);
}
여기까지 모든 구현을 알아보았습니다. 코드가 60줄 가량 되는데, 생각보다는 짧은 편이고 구현도 몇 가지 예외처리를 제외하면 그리 복잡하지 않습니다. 전체 코드는 여기 링크를 참고하시기 바랍니다. (쿼리의 $x$좌표가 실수인 경우에 대한 구현체도 포함되어 있습니다.)
시간복잡도
하나의 직선은 최대 한 번씩 삽입/삭제되고, 한 번 삽입/삭제할 때에는 상수 번의 insert/erase, lower_bound 연산을 사용하므로 삽입/삭제에 드는 총 시간은 $O(nlogn)$입니다.
한 번의 쿼리 연산에서도 상수 번의 lower_bound를 사용하므로 쿼리에 드는 총 시간은 $O(Qlogn)$입니다.
따라서 총 시간복잡도는 $O((n+Q)logn)$입니다.
응용
기본적으로 Convex Hull Trick을 적용하고 싶은데 일차 함수의 기울기가 증가하거나 감소하지 않는 경우 Li-Chao tree 대신 이 방법을 사용할 수 있습니다. 대표적인 문제로는 최근 ICPC 예선 기출문제인 Star Trek이나 반평면 땅따먹기가 있습니다.
또한 set이 기본적으로 제공하는 기능들이 많기 때문에 다른 여러 가지 시도를 해볼 수도 있습니다. iterator로 직선들을 순차적으로 순회할 수도 있고, policy based set을 사용한다면 k번째 직선을 빠르게 찾을 수도 있습니다.
코드를 좀 변형하면 최댓값만을 찾는 것이 아닌 상위 k개의 값을 찾는 k-layer convex hull도 구현할 수 있습니다. 연습문제 링크
결론
여기까지 STL set을 이용한 Convex Hull Trick 구현에 대해 알아보았습니다. 경우에 따라 다를 수도 있겠지만, 제가 구현한 알고리즘은 Li-Chao tree와 실행시간이 거의 비슷했습니다. 알고리즘 자체는 단순하기 때문에 코드를 보지 않고 직접 한 번 구현해 보는 것도 괜찮은 방법이라 생각합니다.
글을 마치겠습니다. 읽어주셔서 감사합니다.