LSH: 유사한 두 데이터 찾기
안녕하세요?
오늘은 두 데이터가 얼마나 유사한지를 계산하는 방법과, 이를 통해 유사한 두 데이터를 찾는 방법인 LSH(Locality Sensitive Hashing)에 대해 설명해보려고 합니다.
Jaccard 유사도
예를 들어 다음과 같은 두 문자열 A, B가 있다고 가정해보겠습니다.
A = “abcabcdefg”
B = “cdefghiabc”
두 문자열을 조금 관찰해보면, “abc”와 “cdefg”라는 공통되는 부분을 가지고 있는 꽤나 유사한 두 문자열임을 알 수 있습니다. 아마 누군가 두 문자열이 유사한지 묻는다면, 저는 유사하다고 답할 것 같습니다.
하지만, 이 두 문자열이 얼마나 비슷한지를 수치적으로 명확하게 나타낼 수 있을까요?
이 때 유사도를 나타내기 위해 사용할 수 있는 한 가지 방법이 바로 Jaccard 유사도를 구하는 방법입니다.
Jaccard 유사도는 두 집합 사이의 유사도를 나타내는 식으로, 두 집합의 교집합의 크기를 두 집합의 합집합의 크기로 나눠서 쉽게 구할 수 있습니다.
$J(A, B) = \frac{|A\cap B|}{|A \cup B|}$
예를 들어 집합 A, B가 각각 A = {1, 2, 5, 8}, B = {2, 3, 5, 7}이라면 합집합의 크기는 6, 교집합의 크기는 2이므로 두 집합의 유사도는 $\frac{1}{3}$이 됩니다.
그럼 이 Jaccard 유사도를 통해, 두 문자열의 유사도도 한 번 구해보도록 하겠습니다.
문자열을 집합으로 나타내기 위해, 적당한 window size를 정해서, 문자열을 슬라이싱하며 집합을 만들어보도록 하겠습니다.
window size를 3으로 잡으면, A, B는 길이 10의 문자열이므로 각각 8개의 부분문자열이 생기게 됩니다.
이제 문자열을 나타내는 집합 A’, B’는 아래와 같습니다. 집합 A’의 중복된 원소는 제거하였습니다.
A’ = {“abc”, “bca”, “cab”, “bcd”, “cde”, “def”, “efg”}
B’ = {“cde”, “def”, “efg”, “fgh”, “ghi”, “hia”, “iab”, “abc”}
둘의 합집합과 교집합을 구해보면 아래와 같습니다.
$|A\cap B|$ = {“abc”, “bca”, “cab”, “bcd”, “cde”, “def”, “efg”, “fgh”, “ghi”, “hia”, “iab”}
$|A\cup B|$ = {“abc”, “cde”, “def”, “efg”}
따라서, 최종적으로 두 문자열의 Jaccard 유사도는 $\frac{4}{11}$가 됨을 알 수 있습니다.
min-hash
이번에는 min-hash라는 또다른 접근법을 살펴보겠습니다.
위 Jaccard 유사도를 구하기 위한 집합을 만들 때처럼, 적당한 window size를 정해서, 이번에는 각각의 문자열의 hash 값을 구해보도록 하겠습니다.
문자열을 슬라이싱하면서 각각의 hash값을 구하는 것은 딱 rabin fingerprint를 사용하기 적합함이 잘 알려져 있습니다.
이 글에서는 Rabin fingerprint에 대한 자세한 설명은 하지 않겠습니다. 이 글에 자세한 설명이 있으니, 관심있는 분들은 한 번 읽어보시기를 추천드립니다.
Rabin fingerprint를 한 마디로 요약하면, 문자열 S의 부분문자열 S[n:n+k]를 이용하여, 다음 부분문자열인 S[n+1:n+k+1]를 O(1)에 계산해낼 수 있는 해시 함수입니다. 따라서, 길이 n인 문자열 전체의, 길이 w인 부분 문자열들의 해시값을 구하는 데에 총 O(n)의 시간으로 가능합니다.
이제 이 각각의 부분문자열에 대해서 구해진 해시값을 모두 minimum연산을 하도록 하겠습니다. 해시 함수는
$f(x) = (s_0 + s_1x + s_2x^2 + … + s_{w - 1}x^{w-1}) % MOD$를 사용할 것이며, x = 999961, MOD = 1000000007을 사용하도록 하겠습니다.
위에서 사용한 문자열 A에 대한 rabin fingerprint와 min-hash값은 아래와 같이 계산됩니다.
| 문자열 | rabin fingerprint |
|---|---|
| “abc” | 375453910 |
| “bca” | 532464830 |
| “cab” | 452459430 |
| “abc” | 375453910 |
| “bcd” | 298448393 |
| “cde” | 221442876 |
| “def” | 144437359 |
| “efg” | 67431842 |
| minimum | 67431842 |
또, 문자열 B에 대한 rabin fingerprint와 min-hash 값은 아래와 같이 계산됩니다.
| 문자열 | rabin fingerprint |
|---|---|
| “cde” | 221442876 |
| “def” | 144437359 |
| “efg” | 67431842 |
| “fgh” | 990426332 |
| “ghi” | 913420815 |
| “hia” | 538464602 |
| “iab” | 452459436 |
| “abc” | 375453910 |
| minimum | 67431842 |
두 문자열의 min-hash 값이 같은 것을 확인할 수 있습니다. 가장 작은 해시값은 내는 “efg” 문자열이 공통이기 때문입니다.
그런데 갑자기 생뚱맞게 hash들의 minimum 연산을 왜 해주었을까요?
그 이유는, 위와 같이 구한 두 문자열의 min-hash 값이 같을 확률은, 두 문자열의 Jaccard 유사도와 같기 때문입니다!
min-hash 값이 같을 확률이 두 문자열의 Jaccard 유사도와 같음은 아래 그림을 보시면 자명하게 이해할 수 있습니다.
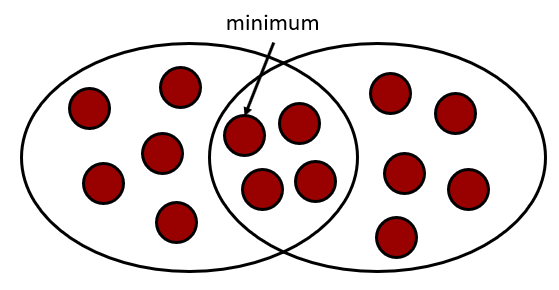
위 그림의 빨간 점들은 각각의 원소들을 의미합니다. 해시 함수가 충분히 이상적이라면, 원소의 해시는 랜덤하게 분포하고, 결국 minimum이 될 확률은 모두 동일하게 $\frac{1}{|A \cup B|}$입니다.
두 집합의 minimum이 같으려면 minimum인 원소가 교집합 내에 있어야 하고, 그 확률이 $\frac{|A \cap B|}{|A \cup B|}$가 되는 것은 자명합니다.
LSH: Locality Sensitive Hashing
이제 마지막으로, min-hash 기법을 사용한 locality sensitive hashing (LSH)을 살펴보겠습니다. LSH도 결국 해시의 일종이지만, 비슷한 데이터는 비슷한 해시값이 나오도록 설계된 해시입니다.
잠시 위의 min-hash를 다시 살펴보도록 하겠습니다.
min-hash를 한 번만 사용하면, 아무리 Jaccard 유사도가 높은 두 데이터라 하더라도 낮은 확률로 다른 min-hash 값이 나오게 됩니다. 마찬가지로, Jaccard 유사도가 높지 않은 두 데이터 또한 낮은 확률로 같은 min-hash 값을 가질 수 있습니다.
다시 말해, false positive 또는 false negative 확률이 그리 낮지 않다는 것을 알 수 있습니다. 따라서 min-hash 자체를 LSH로 사용할 수는 없습니다.
대신, 서로 다른 해시 함수에 대해 min-hash를 반복해서 적용하면, 결국 비슷한 두 데이터는 같은 min-hash 값을 가지는 경우가 많이 발생하고 이를 통해서 비슷한 데이터라고 판단할 수 있습니다.
서로 다른 해시 함수는, 적당한 정수 $a_i$와 $m_i$를 골라 위에서 구한 rabin fingerprint를 다시 한 번 transform 해줌으로서 간단하게 적용할 수 있습니다.
transform은 $x’ = (x * a_i + m_i) % MOD$를 적용하겠습니다.
Transform을 적용하여 위 예시를 다시 한 번 살펴보겠습니다. 상수는 MOD = 1000000007, $a_0 = 2240321$, $a_1 = 5379827$, $a_2 = 1824289$, $m_0 = 2567531$, $m_1 = 6299143$, $m_2 = 3596869$를 사용하도록 하겠습니다.
문자열 A에 대한 LSH값은 아래와 같이 (48854668, 4616700, 120203254)로 계산됩니다.
| 문자열 | rabin fingerprint | $Transform_0$ | $Transform_1$ | $Transform_2$ |
|---|---|---|---|---|
| “abc” | 375453910 | 275784682 | 74433574 | 436822307 |
| “bca” | 532464830 | 134627717 | 655231577 | 729053156 |
| “cab” | 452459430 | 358148983 | 447178682 | 758914227 |
| “abc” | 375453910 | 275784682 | 74433574 | 436822307 |
| “bcd” | 298448393 | 200141344 | 717827954 | 120203254 |
| “cde” | 221442876 | 124498006 | 361222327 | 803584208 |
| “def” | 144437359 | 48854668 | 4616700 | 486965155 |
| “efg” | 67431842 | 973211337 | 648011080 | 170346102 |
| minimum | 67431842 | 48854668 | 4616700 | 120203254 |
또, 문자열 B에 대한 LSH값은 아래와 같이 (48854668, 4616700, 47038642)로 계산됩니다.
| 문자열 | rabin fingerprint | $Transform_0$ | $Transform_1$ | $Transform_2$ |
|---|---|---|---|---|
| “cde” | 221442876 | 124498006 | 361222327 | 803584208 |
| “def” | 144437359 | 48854668 | 4616700 | 486965155 |
| “efg” | 67431842 | 973211337 | 648011080 | 170346102 |
| “fgh” | 990426332 | 897567999 | 291405453 | 853727056 |
| “ghi” | 913420815 | 821924661 | 934799833 | 537108003 |
| “hia” | 538464602 | 549740442 | 390405075 | 47038642 |
| “iab” | 452459436 | 371590909 | 479457644 | 769859961 |
| “abc” | 375453910 | 275784682 | 74433574 | 436822307 |
| minimum | 67431842 | 48854668 | 4616700 | 47038642 |
3개의 값 중 2개가 일치하고, 나머지 하나는 일치하지 않는 것을 확인할 수 있습니다.
보통 LSH의 구현에서는, 이런식으로 min-hash를 r개 묶어서 하나의 LSH로 사용하고, LSH를 b개 생성하여 b개의 LSH 중 하나라도 일치할 경우 같은 블럭으로 판별하는 방법을 사용합니다.
Jaccard 유사도가 p일 때, 각각의 확률은 아래와 같게 됩니다.
LSH가 일치할 확률: $p^r$
b개의 LSH 중 하나라도 일치할 확률: $1 - (1 - p^r)^b$
r = 10, b = 30일 때 Jaccard 유사도에 따른 같은 블럭으로 판별될 확률의 그래프를 그려보면 다음과 같습니다.
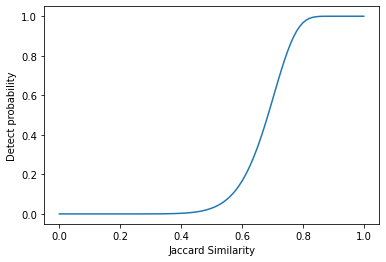
그림을 보면, 일정 threshold를 기준으로 판별 확률이 0과 1에 가깝게 크게 나뉘는 것을 알 수 있습니다.
이렇게 r과 b를 적당히 조절해가며, 원하는 Jaccard 유사도에 따른 판별 확률을 조절할 수 있습니다.
이상으로 글을 마치겠습니다. 감사합니다.
References
글을 쓸 때 참고한 자료는 아래와 같습니다.