Dictionary 기반 압축 알고리즘
안녕하세요?
오늘은 저번 글에 이어, 압축 알고리즘에 대한 설명을 추가로 진행해보려 합니다.
Dictionary Type Data Compression
저번 글에서 소개드린 데이터 압축 기술은 대부분 data entropy를 기반으로 되어 있습니다.
다시 말해, 전체 데이터의 빈도 수를 세고 빈도가 높은 것에 작은 길이의 bit를 할당하는 방식으로 작동하며 data entropy와 최종 압축률이 거의 유사한 값을 가지게 됩니다.
이번 글에서 살펴볼 방법들은 그와는 약간 다른, 출현하는 패턴들을 기억하는 dictionary를 사용하는 압축 방법들입니다.
다만, dictionary type data compression 또한 반복되는 패턴이 많을수록 좋은 압축률을 보이며, 반복되는 패턴이 많다는 것은 해당 데이터가 낮은 entropy를 가지고 있을 가능성이 높다는 것을 시사하기 때문에 압축률이 data entropy와 전혀 무관하다고 보기는 힘듭니다.
Static Dictionary
가장 간단히 생각해볼 수 있는 방식은, static dictionary를 사용하는 방식입니다. 다시 말해, 미리 변환 테이블을 작성해놓고 해당 테이블대로 변환을 시키는 것입니다.
이러한 방식은 출현하는 데이터의 종류가 굉장히 적은 경우에 유용합니다. 예를 들어, C언어로 작성된 코드를 압축한다고 가정해봅시다. C언어에 자주 등장하는 문자열인 if, for, while, ++, int 등은 원래 2~5바이트 정도의 크기를 가지지만, 이러한 문자열들에 대해 따로 변환 테이블을 미리 만들어놓을 경우 효과적으로 파일의 크기를 줄일 수 있습니다.
하지만 static dictionary는 특정한 상황에서만 잘 작동하기 때문에 일반적으로 사용하기에는 무리가 있는 방식입니다.
Adaptive Dictionrary
Adaptive dictionrary는 static dictionary와는 다르게, 현재 파일에서 과거에 등장했던 패턴들을 이용해 dictionary를 구성하는 방식입니다.
대표적인 adaptive dictionary type data compression으로는 LZ계열 알고리즘들이 존재합니다.
LZ 압축 알고리즘은 Abraham Lempel과 Jacob Ziv에 의해 발표되었으며, 두 명의 이름의 앞글자를 따서 이름 붙여졌습니다.
LZ계열 압축 알고리즘에는 수많은 변형들이 존재하지만, 1977년에 발표된 LZ77(또는 LZ1), 1978년에 발표된 LZ78(또는 LZ2)의 작동 방식을 살펴보겠습니다.
LZ77 압축 알고리즘
LZ77은 적당한 window size를 정해놓고, window 내에 현재 패턴과 동일한 문자열 패턴이 출현하는지 찾는 방식으로 작동합니다. 최종적으로 입력 문자열을 (o, l, c)의 tuple들로 변환시키는 것을 목표로 합니다.
알고리즘의 작동을 위해서는 아래의 그림 1과 같이 search buffer, look-ahead buffer 두 가지가 필요합니다.

Search buffer는 이미 처리가 완료된 부분이고, Look-ahead buffer는 이제 압축을 진행해야 하는 부분입니다.
먼저, 현재 Look-ahead buffer에서 처리해야 하는 문자열(abbdabca)과 동일한 prefix를 가지면서, search buffer에서 시작되는 문자열이 존재하는지를 찾습니다. 존재한다면, 그 중 가장 긴 것을 찾습니다.
그림 1에서는, abb가 가장 긴 공통 문자열인 것을 알 수 있습니다. 공통 문자열이 꼭 Search buffer 내에 완전히 포함될 필요는 없습니다. Look-ahead buffer와 겹칠 수도 있습니다. 예를 들어서, 그림 2와 같은 상황은 공통 부분 문자열의 길이가 6인 경우를 나타냅니다.
이제 각 상황을 어떻게 (o, l, c)의 tuple로 변환시키는지 알아보겠습니다.
o(offset)는 search buffer에서 찾은 문자열의 시작점이 look-ahead buffer와 얼마나 떨어져있는지를 의미합니다. l은 겹치는 문자열의 길이이고, 마지막 c는 두 문자열이 더 이상 같지 않게 만드는 문자입니다.
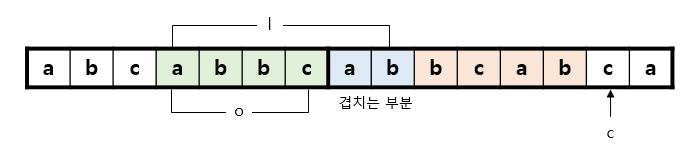
예컨대 그림 2의 상황에서는, (4, 6, ‘c’)로 변환이 되게 됩니다. 이후에는 ‘c’ 이후로 look-ahead buffer를 옮겨 계속 진행하면 됩니다.
이런 식으로 LZ77 알고리즘에서는, 공통되는 문자열을 찾은 후 이를 계속해서 tuple로 변환시켜 나갑니다. 이 때 한 tuple의 크기는 얼마가 될까요?
offest의 최대 크기(search buffer의 크기와 같음)를 O, Window의 크기(search buffer와 look-ahead buffer의 합과 같음)를 W, 전체 문자의 종류를 W라 할 때, tuple 하나를 표현하는 데에 필요한 bit 수는 $\left \lceil \log_2{O} \right \rceil + \left \lceil \log_2{W} \right \rceil + \left \lceil \log_2{C} \right \rceil$만큼의 크기를 가지게 됨을 쉽게 알 수 있습니다.
LZ77에서 또 하나 생각해보아야 할 점은, 가장 긴 공통되는 문자열을 어떻게 찾을지에 대한 것입니다. 흔히 많이 알려진 KMP 알고리즘 등을 사용하면 이를 쉽게 찾아낼 수 있으며, 이 때의 시간 복잡도는 $O(W)$가 되게 됩니다.
LZ77의 Decoding
이번에는 LZ77을 통해 압축된 데이터를 다시 decode하는 법에 대해 생각해보겠습니다.
LZ77 알고리즘을 통해 압축된 데이터를 다시 decode하는 것은 굉장히 간단합니다.
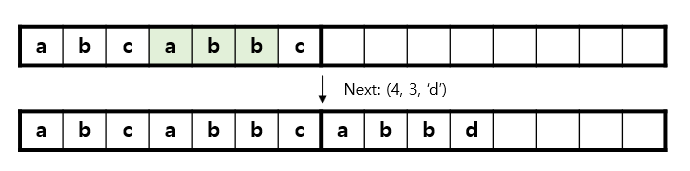
아래의 그림 3과 같이, 현재까지 decode된 문자열이 abcabbc이고, 그 다음 처리해야 할 tuple이 (4, 3, ‘d’)라고 가정해봅시다. 이 경우 왼쪽으로 4만큼 움직인 후, 해당 위치부터 3개의 문자를 복사한 뒤, 마지막에 ‘d’를 붙이는 것으로 해당 tuple의 처리가 완료됩니다.
LZ78 압축 알고리즘
LZ77 알고리즘은 굉장히 심플한 알고리즘이지만, 몇 가지 단점을 가지고 있습니다. 그 중 가장 치명적인 문제로는 LZ77 알고리즘은 search buffer size 내에서만 탐색을 진행하기 반복되는 문자열이 비교적 가까운 거리에 위치해야 한다는 문제점이 있습니다.
가장 worst한 case로, 만약 압축을 진행할 문자열이 주기적으로 반복되는 문자열인데 주기가 search buffer size보다 클 경우 전혀 압축을 할 수 없게 됩니다.
LZ78 압축 알고리즘은 search buffer라는 조건을 없애 이러한 문제점을 극복하였습니다.
LZ78 압축 알고리즘은 전체 데이터를 압축할 때까지 계속해서 dictionary를 유지합니다.
가장 먼저, dictionary에서 현재 압축할 부분과 같은 가장 긴 패턴을 찾아 이를 바꾸고, 해당 패턴 뒤에 한 글자를 더 덧붙인 패턴을 dictionary에 추가하는 것을 반복합니다.
LZ78도 LZ77과 마찬가지로 문자열을 tuple로 바꾸게 됩니다. 하지만 LZ78에서 사용하는 tuple은 두 개의 성분으로 이루어져 있으며, (i, c)로 일치하는 문자열 패턴의 인덱스 i와 패턴 뒤에 놓이는 문자 c 두 개로 이루어져 있습니다.
예시를 한 번 살펴보겠습니다. abccabcdabbcddab라는 길이 16짜리 문자열을 압축하는 상황을 한 번 살펴보겠습니다.
가장 초반에는 dictionary는 비어있는 채로 시작합니다. a라는 문자가 없으므로, 이를 (0, ‘a’)로 바꾸어준 후 문자열 ‘a’를 dictionary에 추가합니다. 마찬가지로 b, c에 대해서도 (0, ‘b’), (0, ‘c’)로 바꾸고 dictionary에 추가합니다.

그 다음의 경우, ‘c’라는 문자열이 이미 사전에 들어있습니다. 이것이 최장 길이의 문자열이므로, 해당 인덱스인 3을 적어둔 후, 다음 문자인 ‘a’를 추가하여 (3, ‘a’)를 저장합니다. 또 이를 사전에 추가해줍니다. 마찬가지로, ‘b’라는 문자열이 이미 사전에 들어있으므로 (2, ‘c’)를 저장하고 bc를 사전에 추가합니다.

이와 같은 과정을 반복하여 최종적으로 얻는 output과 사전은 아래의 그림 6과 같습니다.

LZ78의 Decoding
그렇다면 이번에는 output을 가지고 원래 문자열을 다시 복구해낼 수 있을까요? 우리에게는 encoding을 진행할 때 가지고 있던 dictionary 정보도 없는데 말입니다.
놀랍게도 이는 가능합니다. tuple 하나가 생성될 때마다 사전의 index가 하나씩 추가된다는 점에 착안하여, tuple을 하나씩 추가할 때마다 dictionary를 하나씩 복원하며 진행하면 encoding과 거의 비슷한 방식으로 원래 문자열을 복구해 낼 수 있습니다.
아래의 그림 7은 복구 과정의 초반부를 나타낸 그림입니다.
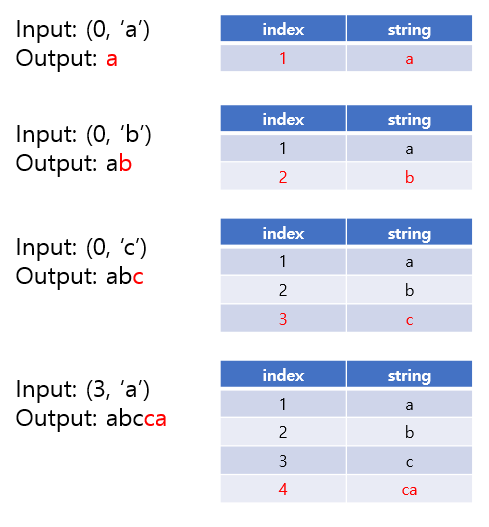
(i, c)라는 tuple이 이번에는 입력으로 들어올 때, dictionary의 해당 index번에 저장된 문자열을 출력한 후, c를 덧붙여주면 가능합니다. 마찬가지로 dictionary에 현재 tuple을 통해 생성된 문자를 추가해주면 됩니다.
LZ78의 encode과정은 트라이 자료구조를 사용하여 구현 가능합니다. LZ78 압축 알고리즘의 경우 dictionary의 크기가 무한정 늘어날 수 있으므로, 메모리 요구량이 큰 단점으로 작용할 수 있습니다. 이를 개선하기 위해 dictionary의 크기의 상한을 정해주는 등의 최적화를 적용할 수 있으며, 이러한 방식들은 변형된 많은 알고리즘에 적용되어 있습니다.
Reference
이상으로 LZ77과 LZ78 알고리즘에 대해 살펴보았습니다.
글을 작성하는 데에 참고한 도서는 아래와 같습니다.
Sayood, Khalid. Introduction to data compression. Morgan Kaufmann, 2017.