임의의 원소를 수정할 수 있는 우선순위 큐
서론
힙 (Heap)은 그 간단한 구조와 시간 / 공간 측면에서의 여러 장점들 때문에 문제 풀이뿐만 아니라 실무에서도 우선순위 큐로서 널리 애용되는 자료구조입니다. C++의 std::priority_queue, Java의 java.util.PriorityQueue, Python의 heapq1 등 고수준 언어의 자료구조 라이브러리에서 웬만하면 지원을 해주기도 합니다.
우선순위 큐를 라이브러리로만 접하면 기능이 매우 적은 것에 대해 실망할 수도 있습니다. 대체로 원소를 삽입하는 기능과, 최대 혹은 최솟값을 확인하고 제거하는 연산이 전부이기 때문입니다. 그런데 사실 힙에는 그 외에도 많은 가능성들이 숨어있습니다. 단순한 형태의 구현체에서는 수행하기 어려운 연산들을 여러 변형을 통해 지원하게 하거나, 더욱 개선된 시간 복잡도를 가지도록 만드는 것도 가능합니다. 일반적으로 많이 알려져 있는 것 중 하나가 피보나치 힙으로, 최솟값(혹은 최댓값) 삭제 연산을 제외한 모든 연산을 $Θ(1)$에 수행할 수 있는 자료구조입니다. 그러나 이런 것들은 구현체가 매우 복잡할 뿐더러 이론상 시간 복잡도만 작을 뿐 실제로 사용될 법한 상황에서는 오히려 느리기 때문에 실무에서 사용될 일이 거의 없다고 합니다.
이 글에서는 가장 기본적이고 널리 쓰이는 힙의 형태인 binary heap을 개선하여 임의의 원소를 수정하는 것이 가능하게 만들어 보도록 하겠습니다. 또한 이것이 왜 라이브러리 상에는 잘 구현되지 않는지도 알아보도록 하겠습니다.
Binary Heap
먼저 binary heap의 형태를 간단히 짚고 넘어가려 합니다. 기본적으로 힙이 지원하는 연산들과 장단점을 보고, 이를 어떻게 개선시킬 수 있는지 비교하기 위함입니다. 구체적인 동작 원리에 대해서는 이 글에서 따로 설명하지는 않겠습니다.
Binary heap은 일반적으로 완전 이진 트리2의 형태를 사용하며, 단순한 1차원 배열로 이를 구현합니다. 트리의 인덱싱은 세그먼트 트리에서 사용하는 것과 같은 구조로, $0$부터 시작해서 $i$번 노드의 자식을 $2i + 1$과 $2i + 2$로 두는 방식 또는 $1$부터 시작해서 $i$번 노드의 자식을 $2i$와 $2i + 1$로 두는 방식을 사용합니다. 이 글에서는 편의상 $1$번을 루트로 하는 형태를 사용하겠습니다.
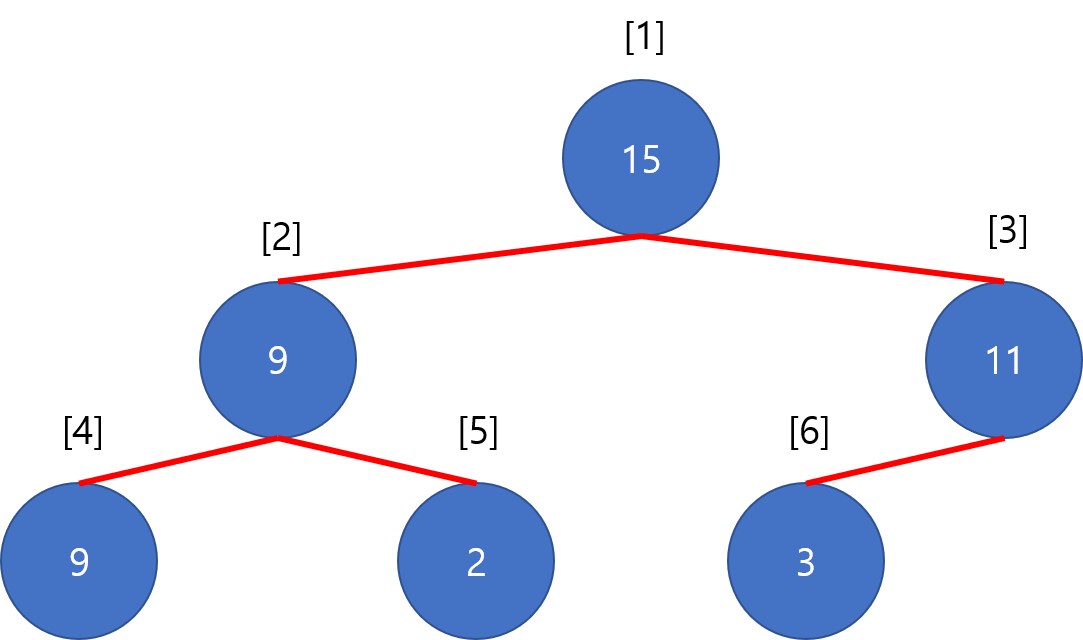
가장 큰 원소를 루트에 두는 max heap의 경우 부모 노드는 반드시 두 자식 노드들보다 작지 않은 값이어야 합니다. 두 자식 노드들끼리의 대소관계에는 제약이 없습니다.
이러한 구조에 일반적으로 제공되는 연산은 다음과 같습니다.
- find-max: 힙에서 가장 큰 원소, 즉, 루트에 있는 값을 얻어옵니다. 시간 복잡도는 $O(1)$입니다.
- insert: 힙에 새로운 원소를 추가합니다. 원소 추가 후 힙의 형태를 복원하는 데에 $O(\log{n})$의 시간이 소요됩니다.
- delete-max: 힙에서 가장 큰 원소를 삭제합니다. 원소 삭제 후 힙의 형태를 복원하는 데에 $O(\log{n})$의 시간이 소요됩니다.
이처럼 기본적인 형태의 힙에는 할 수 있는 연산이 많지 않습니다. 사실상 바로 확인할 수 있는 원소는 루트에 있는 노드뿐이고, 나머지 노드에 대해서는 알아낼 수 있는 유용한 정보가 그다지 없기 때문입니다. 물론 이것만으로도 항상 전체에서 최대가 되는 값을 $O(1)$에 알 수 있고 그러한 값을 제거하거나 새로운 값을 추가하는 것이 모두 $O(\log{n})$ 시간에 된다는 것만으로도 충분히 매력적이고, 여러 기능을 추가할 수 있는 균형 이진 트리3에 비해 나머지 연산들이 훨씬 시간 / 공간 면에서 효율적이기 때문에 제거 연산이 필요하지 않은 경우에는 힙 구조를 사용하는 것이 좋다고 할 수 있습니다.
개선
이러한 힙에도 임의의 원소를 $O(\log{n})$ 시간에 변경하거나 삭제하는 기능을 추가하는 것이 가능합니다. 또한 이는 많은 경우에 균형 이진 트리에 비해 훨씬 나은 성능을 보여줄 수도 있습니다. 그러나 이러한 힙을 구현하는 데에는 여러 제약 조건이 있어, 제한적인 상황에서만 사용할 수 있습니다.
그 이유는 바꾸려는 원소가 힙에서 어디에 위치하는지 알 수 있어야 하기 때문입니다. 즉, 힙의 특정 원소에 대한 탐색 요청이 들어왔을 때, 그 원소의 값 또는 id가 될 수 있는 요소와 힙 내에서의 인덱스가 매핑이 되어 있어야 이와 같은 기능을 구현할 수 있습니다.
매핑 방법
크게 다음의 두 방법을 통해 매핑하는 것이 가능합니다.
- 원소 (구조체) 내부에 힙 내에서의 인덱스를 저장하는 변수를 선언하고, 실제 힙에는 각 원소에 대한 포인터를 저장합니다. 원소에 대한 변경을 할 때에는 내부에 저장된 인덱스 값을 이용하여 원소의 위치를 찾아 그 지점에서 시작합니다.
- 원소를 특정할 수 있는 id (ex: 번호) 등과 원소 자체를 서로 매핑합니다. 해당 id를 통해 힙 내에서의 인덱스를 빠르게 찾을 수 있게 하고, 원소가 이동할 때마다 매핑된 인덱스도 함께 변경해 줍니다.
각각에는 장단점이 있으나, 두 경우 모두 일반화된 라이브러리에서 사용하기에는 어려운 면이 있습니다. 1번의 경우, 사용자가 원소의 복사본을 만들 수 없다는 점이 장애물이 됩니다. 원소를 항상 해당 원소 자체로 사용해야만 힙 내에서 변화가 생겼을 때 이후에도 해당 원소에 대한 변경이 가능하기 때문입니다. 2번의 경우, 매핑 방법을 사용자가 제공해주어야 한다는 점이 어려움이 되며, id가 정수가 아니거나 범위가 큰 경우 매핑에 드는 비용이 커져 효율성을 도리어 저하시킨다는 것도 문제로 작용합니다.
이러한 이유들로 인해 원소의 변경이나 삭제는 라이브러리 차원에서 직접적으로 지원하기에는 어려움이 있으나, 사용자가 직접 힙을 구현하는 경우에는 문제점을 극복하고 보다 효율적으로 동작하는 자료구조를 만들어낼 수 있습니다.
임의의 원소 변경
(최대 힙에서) 원소를 변경하는 경우에는 다음의 두 가지 경우가 있습니다.
- 원소의 값이 이전보다 감소했을 때: 기존의 위치보다 더 아래로 내려가야 할 수 있습니다.
- 원소의 값이 이전보다 증가했을 때: 기존의 위치보다 더 위쪽으로 올라가야 할 수 있습니다.
전자는 힙이 아닌 배열을 힙으로 만들 때 (heapify)에도 각 원소에 대해 수행해주는 연산입니다. 왼쪽 자식과 오른쪽 자식 중 더 큰 것보다 자신이 더 작을 때 둘의 위치를 바꾸는 것을 반복해나가는 연산입니다.
반대 과정 역시 가능합니다. 자신이 부모보다 더 큰 경우 둘의 위치를 바꾸는 것을 반복해나가는 과정이고, 이 역시 힙의 구조를 유지할 수 있습니다.
임의의 원소 삭제
원소 삭제는 pop 연산에서 하는 것과 비슷합니다. 힙의 마지막 원소를 현재 원소 자리에 끼워넣고, 원소 변경을 할 때와 마찬가지로 값의 변화 방향에 따라 위로 올리거나 아래로 내려서 구현할 수 있습니다.
이 과정들에서 중요한 것은 힙 내에서의 인덱스가 변할 때마다 매핑된 인덱스 역시 함께 변경이 이루어져야 한다는 점입니다. 그래야 이후에도 특정 원소를 변경하고 싶을 때 그 위치를 바로 찾아낼 수 있기 때문입니다.
구현 코드
다음은 2번 방법을 사용하여 이와 같은 힙을 구현한 코드입니다. 최소 힙으로 구현하였고, w라는 원소의 값에 의해 우선순위가 결정되며, 원소를 특정하는 id로 i의 값이 사용됩니다. i는 0부터 n-1까지의 값을 가지는 경우를 가정합니다.
#include <iostream>
#include <random>
#include <ctime>
#include <set>
using namespace std;
const int N = 10000000;
struct Elem {
int i, w;
bool operator<(const Elem &o) const {
return w == o.w ? i < o.i : w < o.w;
}
};
struct PQ {
Elem *arr;
int *pos;
int sz;
PQ(int mx) : sz(0)
{
arr = new Elem[mx + 1];
pos = new int[mx + 1];
}
~PQ()
{
delete[] arr;
delete[] pos;
}
void push(int i, int w)
{
++sz;
arr[sz] = { i, w };
pos[i] = sz;
up(sz);
}
void change(int i, int w)
{
int cur = pos[i];
int k = arr[cur].w;
arr[cur].w = w;
if (k < w)
down(cur);
else
up(cur);
}
void up(int cur)
{
while (cur > 1)
{
if (arr[cur].w >= arr[cur >> 1].w)
break;
swap(arr[cur], arr[cur >> 1]);
pos[arr[cur].i] = cur;
cur >>= 1;
}
pos[arr[cur].i] = cur;
}
void down(int cur)
{
while ((cur << 1) <= sz)
{
int mx;
if ((cur << 1) == sz || (arr[cur << 1].w < arr[(cur << 1) + 1].w))
mx = (cur << 1);
else
mx = (cur << 1) + 1;
if (arr[cur].w <= arr[mx].w)
break;
swap(arr[cur], arr[mx]);
pos[arr[cur].i] = cur;
cur = mx;
}
pos[arr[cur].i] = cur;
}
int pop()
{
int ret = arr[1].i;
arr[1] = arr[sz--];
pos[arr[1].i] = 1;
down(1);
return ret;
}
void del(int i)
{
int cur = pos[i];
int k = arr[cur].w;
arr[cur] = arr[sz--];
pos[arr[cur].i] = cur;
if (arr[cur].w > k)
down(cur);
else
up(cur);
}
};
push, pop의 역할은 일반적인 우선순위 큐에서와 동일하고, up은 원소를 위로 올리는 연산, down은 원소를 아래로 내리는 연산으로 위에서 설명한 것과 같습니다. 주의 깊게 볼 것은 pos 배열이 사용되는 방법입니다.
pos[i]는 i번 원소가 힙 내에서 위치한 인덱스를 의미합니다. 이를 위해 맨 처음 원소가 삽입될 때 push 함수에서 원소를 힙의 끝 (sz)에 추가한 뒤 그 위치를 pos[i]에 기록해두고 있는 것을 볼 수 있습니다. 또한 arr[sz].i를 i로 설정함으로써 원소의 위치가 바뀔 때 pos 배열을 역으로 참조할 수 있게도 설정했습니다.
이후 up과 down 함수에서 원소가 옮겨갈 때마다 pos[arr[cur].i]를 함께 변경시켜 줌으로써 변화된 위치를 같이 기록해나가고, 이로 인해 힙 내의 모든 원소는 항상 pos 배열에 올바르게 매핑된 상태를 유지할 수 있게 됩니다.
그 덕분에 일반적인 우선순위 큐에서는 지원되지 못하는 기능인 change 함수와 del 함수가 만들어질 수 있게 되었습니다. change 함수는 변화된 원소가 기존 값보다 커졌는지, 혹은 작아졌는지에 따라 up 또는 down 함수를 호출하고, del 함수 역시 마지막에 있던 원소를 현재 자리에 옮겨넣고 마찬가지로 두 함수 중 하나를 호출하여 힙의 형태를 유지시키는 것을 볼 수 있습니다.
테스트 코드
다음은 이 우선순위 큐의 성능을 set과 비교하여 실험하기 위한 main 함수입니다.
int main()
{
mt19937 mt((unsigned int)time(NULL));
Elem *arr = new Elem[N];
for (int i = 0; i < N; i++)
arr[i] = { i, (int)(mt() >> 1) };
clock_t st, ed;
PQ pq(N);
set<Elem> s;
cout.precision(3);
cout << fixed;
cout << "Push & pop" << endl;
cout << "Heap: ";
cout.flush();
st = clock();
for (int i = 0; i < N; i++)
pq.push(i, arr[i].w);
for (int i = 0; i < N; i++)
pq.pop();
ed = clock();
cout << (ed - st) / double(CLOCKS_PER_SEC) << "s" << endl;
cout << "Set: ";
cout.flush();
st = clock();
for (int i = 0; i < N; i++)
s.insert(arr[i]);
for (int i = 0; i < N; i++)
s.erase(s.begin());
ed = clock();
cout << (ed - st) / double(CLOCKS_PER_SEC) << "s" << endl << endl;
cout << "Modify" << endl;
for (int i = 0; i < N; i++)
pq.push(i, arr[i].w);
for (int i = 0; i < N; i++)
s.insert(arr[i]);
cout << "Heap: ";
cout.flush();
st = clock();
for (int i = 0; i < N; i++)
pq.change(i, arr[N - i - 1].w);
ed = clock();
cout << (ed - st) / double(CLOCKS_PER_SEC) << "s" << endl;
cout << "Set: ";
cout.flush();
st = clock();
for (int i = 0; i < N; i++)
{
s.erase(arr[i]);
s.insert({ i, arr[N - i - 1].w });
}
ed = clock();
cout << (ed - st) / double(CLOCKS_PER_SEC) << "s" << endl << endl;
while (pq.sz)
pq.pop();
s.clear();
cout << "Delete in random order" << endl;
int *perm = new int[N];
for (int i = 0; i < N; i++)
perm[i] = i;
shuffle(perm, perm + N, mt);
for (int i = 0; i < N; i++)
pq.push(i, arr[i].w);
for (int i = 0; i < N; i++)
s.insert(arr[i]);
cout << "Heap: ";
cout.flush();
st = clock();
for (int i = 0; i < N; i++)
pq.del(perm[i]);
ed = clock();
cout << (ed - st) / double(CLOCKS_PER_SEC) << "s" << endl;
cout << "Set: ";
cout.flush();
st = clock();
for (int i = 0; i < N; i++)
s.erase(arr[perm[i]]);
ed = clock();
cout << (ed - st) / double(CLOCKS_PER_SEC) << "s" << endl << endl;
delete[] arr;
delete[] perm;
}
총 세 개의 실험을 수행하였으며, 각각은 다음과 같습니다.
- Push & pop: 1000만 개의 원소를 삽입하고, 가장 작은 것부터 전부 빼내는 데에 걸린 시간을 측정합니다.
- Modify: 1000만 개의 원소가 이미 삽입된 상태에서, 모든 원소의 값을 한 번씩 다른 값으로 바꾸는 시간을 측정합니다.
set의 경우 원소의 값을 직접 바꾸는 것이 불가능하므로, 해당 원소를 제거하고 바꾼 값을 다시 삽입하는 방식을 사용합니다. - Delete in random order: 1000만 개의 원소가 이미 삽입된 상태에서, 임의의 순서대로 원소를 삭제합니다.
위 코드를 실행한 결과는 다음과 같습니다.
Push & pop
Heap: 5.516s
Set: 10.282s
Modify
Heap: 0.275s
Set: 25.325s
Delete in random order
Heap: 1.862s
Set: 14.047s
단순히 순차적으로 원소를 삽입하고 삭제하는 것은 약 2배 정도 차이로, 이것만으로도 제법 큰 차이가 나는 것을 볼 수 있습니다. 물론 이것은 일반적인 우선순위 큐에서도 가능한 작업이고 오히려 개선된 버전보다 더욱 빠르게 동작할 것입니다.
개선된 우선순위 큐의 진가는 나머지 두 실험에서 드러납니다. 중간의 원소의 값을 직접 바꾸지 못해 삭제 후 재삽입을 해야 하는 set은 무려 25초가 소요된 반면에, 개선된 우선순위 큐는 단 0.275초 만에 모든 작업을 완료했습니다. 배율로는 무려 약 92배나 빠른 것입니다. 일반적인 우선순위 큐에서는 할 수 없는 일이면서 set에서는 너무나 느린 작업을 개선된 우선순위 큐에서는 빠르게 해낼 수 있습니다.
또한 랜덤 순서로 원소를 삭제하는 것 역시 굉장한 차이가 발생합니다. 이 차이가 pop보다 훨씬 크게 나타나는 것은, 힙에서는 pop 수행 시 마지막 원소가 루트로 올라가 평균적으로 많은 단계를 내려와야 하는 반면에 중간의 원소를 삭제하는 것은 상대적으로 적은 단계를 이동할 가능성이 크기 때문에 빠르기도 하고, 반면에 set의 begin()을 삭제하는 것은 빠르지만 임의의 원소를 삭제하는 것은 해당 원소를 찾는 데에 걸리는 시간이 추가되기 때문에 오히려 느려지기 때문입니다.
다만 여전히 힙에서는 lower / upper bound를 구현할 수 없고 최소와 최대를 동시에 빠르게 얻어낼 수 없으며, 원소의 id를 순차적으로 발급할 수 있는 형태여야 한다는 점은 한계점으로 남습니다.
활용
임의의 원소를 변경하는 기능이 추가된 우선순위 큐는 다음과 같은 활용처들이 존재합니다.
- 다익스트라 알고리즘 개선: 일반적으로 라이브러리에서 제공하는 우선순위 큐를 사용하여 다익스트라 알고리즘을 수행하면 $O((V+E)\log{E})$ 시간이 소요됩니다. 이는 다익스트라 알고리즘을 일반적으로 구현하는 방식에서 각 정점의 거리가 갱신될 때마다 우선순위 큐에 정점과 변경된 거리 쌍을 다시 한 번 push하기 때문에, 우선순위 큐 내에 원소가 최대 $O(E)$개 들어갈 수 있기 때문입니다. 하지만 개선된 우선순위 큐를 사용하면 시간 복잡도를 $O((V+E)\log{V})$로 줄일 수 있습니다. 각 정점이 큐에 최대 한 개만 들어가도록 제한한 상태에서 거리값만 바꿀 수 있기 때문입니다. $\log{E}$와 $\log{V}$가 크게 차이날 일이 많지 않다고 해도, 힙의 크기가 커지면 리프 근처에서 캐시 미스가 매우 자주 발생한다는 점을 고려하면 이 크기를 최소화하는 것이 성능상으로 크게 도움이 될 수도 있습니다.
- 스케줄러: 작업에 우선순위가 있는 스케줄러에서 중도에 특정 작업이 불필요해지거나 우선순위가 바뀌어야 하는 경우가 있습니다. 이런 경우 일반적인 우선순위 큐에서는 주로 업데이트된 정보를 우선순위 큐에 그대로 삽입하고 오래된 정보가 pop으로 빠질 때까지 기다린 후 그 내용이 최신 정보인지를 확인하는 방법을 사용하지만, 미리 제거하여 큐의 크기를 줄일 수 있다면 더 효율적이고 일관성도 확보될 것입니다. 이를 균형 이진 트리를 사용하여 해결하려는 경우 균형을 잡는 오버헤드가 커서 느리기 때문에, 개선된 우선순위 큐가 그 대안이 될 수 있습니다.
마치며
이 글에서는 항상 개발자의 근처에 존재하지만 그다지 정체를 확인할 일이 없던 자료구조인 힙의 가능성을 보였습니다. 단순히 빠르게 최소 혹은 최댓값을 얻어낼 수 있는 자료구조를 넘어, 임의의 원소에 접근하면서도 크게 효율성을 저하시키지 않는 방법을 확인할 수 있었습니다.
힙에는 이외에도 다양한 변형이 존재하며 각각의 장단점이 존재합니다. 삽입, 수정 등을 $O(1)$에 할 수 있거나 두 힙을 $O(\log{n})$이나 $O(\log{1})$에 합칠 수 있는 구조 등, 기본형만을 사용하는 데에 그치지 않고 상황에 따라 적절한 힙 구조가 있는지를 확인해보는 것도 좋을 것입니다.
참고 자료
- https://en.wikipedia.org/wiki/Heap_(data_structure)
-
Queue.PriorityQueue도 내부적으로heapq를 사용하지만,Queue모듈이 멀티스레드용이기 때문에 사용에 일부 제약이 있습니다. ↩ -
인덱싱 방법에 따라 $n$개의 원소가 $[0]$ ~ $[n-1]$ 또는 $[1]$ ~ $[n]$에 만들어집니다. ↩
-
Red-Black Tree 또는 AVL Tree 등이 있으며, C++의
std::set등이 이러한 구조를 사용합니다. 이러한 구조에서는 최대 / 최소를 모두 $O(1)$에 얻어내는 것이 가능하고, 구조를 변화시키지 않고 증가 / 감소하는 순으로 순회도 $O(n)$에 가능합니다. ↩