Gumbel softmax
소개
언어 모델, 어텐션 메커니즘, 강화학습 등 다양한 문제에서 이산확률변수(discrete random variable)를 모델링해야 할 때가 있습니다. 하지만, 뉴럴 네트워크를 가지고 이러한 이산확률변수를 표현하는 것은 매우 어렵습니다. 왜냐하면 역전파(backpropagation) 알고리즘으로 미분 불가능(혹은 기울기가 0)인 레이어를 학습할 수 없기 때문입니다.
이러한 이산적인 연산을 sigmoid나 softmax 함수로 대체하는 것을 고려해 볼 수도 있습니다. 하지만, 이산적인 상태를 표현해야 하는 경우에는 이러한 함수를 사용할 수 없습니다. 또 다른 방법인 몬테카를로 방식으로 이산적인 연산의 gradient를 추정할 수 있지만 이 경우 큰 varience로 인해 학습이 불안정한 문제가 있습니다.
논문 “Categorical Reparameterization with Gumbel-Softmax”은 ICLR 2017에 accept된 논문으로 Gumbel-Softmax라는 것을 제안하여 카테고리 분포를 역전파 알고리즘으로 학습할 수 있도록 하였습니다. 참고로 동일한 시기에 논문 “The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables”에서도 카테고리 분포를 학습할 수 있는 동일한 테크닉을 소개하였습니다. 이번 글에서는 두 논문이 소개하고 있는 방법에 대해서 알아봅시다.
Gumbel distribution
Gumbel 분포는 주로 샘플의 최댓값 혹은 최솟값의 분포를 모델링하기 위해 사용됩니다. Gumbel 분포의 확률 밀도 함수(probability density function)는 $f(x;\mu,\beta)={1\over \beta} e^{-(z+e^{-z})}, z={ {x-\mu}\over \beta}$이고 누적 분포 함수(cumulative distribution function)는 $F(x;\mu,\beta)=e^{-e^{-(x-\mu)/\beta}}$입니다. Gumbel 분포의 확률 밀도 함수는 그림과 같이 Positively skewed 한 모양을 가집니다.
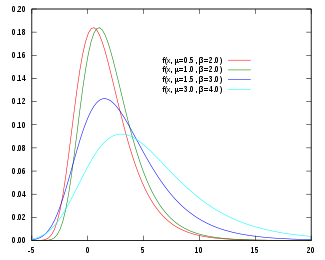
출처: https://en.wikipedia.org/wiki/Gumbel_distribution
다음 절에서 소개할 Gumbel-softmax는 $\mu$가 0이고 $\beta$가 1인 경우인 Standard gumbel 분포를 사용합니다.
standard gumbel 분포의 역 누적 분포 함수(inverse cumulative distribution function)는 $Q(u)=-\ln(-\ln(u))$입니다. 따라서 $(0,1)$에서 uniform하게 샘플 $u$를 뽑으면 standard gumbel 분포에서 샘플을 $Q(u)$로 얻을 수 있습니다.
Gumbel-Softmax
Gumbel-Softmax 분포는 simplex 위에서 정의되고 카테고리 분포에서의 샘플을 추정할 수 있는 분포입니다. $z$를 클래스 확률이 $\pi=(\pi_1, \pi_2, …, \pi_k)$로 주어졌을 때 카테고리 확률 변수라고 합시다. 카테고리 분포의 샘플은 $k$ 차원의 원 핫 벡터로 표현할 수 있고 $z$의 기댓값을 $(\pi_1, \pi_2, …, \pi_k)$로 표현할 수 있습니다.
$g_1, g_2, …, g_k$이 standard gumbel 분포를 따르고 독립적이라고 합시다. Gumbel-Max 트릭을 사용하면 클래스 확률이 $\pi$인 카테고리 분포에서의 샘플 $z$을 다음과 같이 나타낼 수 있습니다.
$z=\text{one_hot}(\argmax_i[g_i+\log \pi_i])$
$\argmax$는 미분이 불가능하기 때문에 softmax 함수와 temperature $\tau$를 가지고 미분가능한 형태로 근사합니다. 그래서 $z$ 대신에 다음과 같이 정의되는 $y=(y_1, …, y_k)$를 사용합니다.
$y_i={\exp((\ln(\pi_i)+g_i)/\tau) \over {\sum_{j=1}^k \exp((\ln(\pi_j)+g_j)/\tau)}}, i=1,..,k$
$\tau$가 0에 가까워질 수록 Gumbel-Softmax의 샘플이 원 핫에 가까워지고 분포가 카테고리 분포와 비슷하게 됩니다. 반대로 $\tau$가 커지면 샘플이 원 핫 모양이 아니게 되고 분포가 uniform 분포에 가까워집니다.

실제로 그림을 보면 $\tau=0.1$일 때 Gumbel-Softmax의 기댓값이 카테고리 분포의 기댓값과 유사하고 $\tau=10$일 때는 Gumbel-Softmax의 각 클래스 확률이 uniform하게 변하는 것을 확인할 수 있습니다.
Gumbel-Softmax 분포는 $\tau>0$일 때 smooth하기 때문에 gradient $\partial y \over \partial \pi$를 구할 수 있습니다. 따라서 카테고리 샘플 대신에 Gumbel-Softmax 샘플을 사용하면 역전파 알고리즘을 통해 gradient를 구할 수 있습니다.
앞에서 말했듯이 Gumbel-Softmax 샘플은 미분 가능하지만 $\tau$가 0이 아닐 때 카테고리 샘플과 정확히 일치하지는 않습니다. $\tau$를 0에 가깝게 하면 더 정확한 근사치를 얻을 수 있지만 gradient의 분산이 커지는 단점이 있습니다. 그래서 실제로는 $\tau$를 큰 값에서 시작해서 0에 가까운 값으로 줄여가며 학습합니다.
Straight-through Gumbel-Softmax estimator
시퀀스 모델링이나 어텐션 같은 히든 표현의 경우 원 핫 벡터를 relaxations해서 사용할 수 있지만 이산적인 상태가 필요한 경우에는 다른 방법을 써야 합니다. 저자는 forward시 $\argmax$를 통해 원 핫 벡터 $z$를 취하고 backward시 $\nabla_\theta z$ 대신에 $\nabla_\theta y$를 사용하는 Straight-Through (ST) Gumbel Estimator를 제안했습니다. ST Gumbel Estimator는 $\tau$가 클수록 편향된 미분 값을 추정하기 때문에 적절한 $\tau$를 설정해야 합니다.
결과
Gumbel-Softmax와 ST Gumbel-Softmax는 다양한 테스크에서 이산확률분포를 학습하는 기존의 방법보다 좋은 성능을 보여주었습니다.

VAE 성능 비교
VAE 구현
Gumbel-Softmax를 사용하여 Variational autoencoder(VAE)를 간단하게 구현해보았습니다. VAE는 아래 식에서 우변 ELBO를 최대화하도록 학습합니다.
| $\log p_\theta (x) \geq \mathbb{E}{q\phi(y | x)}[\log p_\theta(x | y)]-KL(q_\phi(y | x) | p_\theta(y))$ |
논문과 같이 Gumbel prior 대신 카테고리 prior를 사용했고 MINIST 이미지 데이터 셋으로 학습시켰습니다.
import torch
import torch.nn.functional as F
import torch.nn as nn
from torch.optim import Adam
from torchvision import datasets, transforms
from torchvision.utils import save_image
epochs = 10
batch_size = 64
tau = 1.0
hard = True
n_vars = 20
n_classes = 10
print_freq = 100
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
dataloader = torch.utils.data.DataLoader(
datasets.MNIST('./data', train=True, download=True, transform=transforms.ToTensor()),
batch_size=batch_size,
shuffle=True
)
def gumbel_softmax_sample(logits, tau, eps=1e-20):
u = torch.rand(logits.shape, device=logits.get_device())
g = -torch.log(-torch.log(u + eps) + eps)
x = logits + g
return F.softmax(x / tau, dim=-1)
def gumbel_softmax(logits, tau, hard=False):
y = gumbel_softmax_sample(logits, tau)
if not hard:
return y
n_classes = y.shape[-1]
z = torch.argmax(y, dim=-1)
z = F.one_hot(z, n_classes)
z = (z - y).detach() + y
return z
class GumbelVAE(nn.Module):
def __init__(self):
super(GumbelVAE, self).__init__()
self.encoder = nn.Sequential(
nn.Linear(784, 512),
nn.ReLU(True),
nn.Linear(512, 256),
nn.ReLU(True),
nn.Linear(256, n_vars * n_classes)
)
self.decoder = nn.Sequential(
nn.Linear(n_vars * n_classes, 256),
nn.ReLU(True),
nn.Linear(256, 512),
nn.ReLU(True),
nn.Linear(512, 784),
nn.Sigmoid()
)
def forward(self, x):
x = self.encode(x)
logits = x.view(x.shape[0], n_vars, n_classes)
q = F.softmax(logits, dim=-1).view(x.shape[0], -1)
x = self.decode(gumbel_softmax(logits, tau, hard).view(x.shape[0], -1))
return x, q
def encode(self, x):
return self.encoder(x)
def decode(self, x):
return self.decoder(x)
def compute_loss(pred, target, q):
rc_loss = F.binary_cross_entropy(pred, target, reduction='sum') / target.shape[0]
kl = (q * torch.log(q * n_classes)).sum(dim=-1).mean()
loss = rc_loss + kl
return loss
model = GumbelVAE().to(device)
optimizer = Adam(model.parameters())
for epoch in range(epochs):
# training
for iteration, (data, _) in enumerate(dataloader):
data = data.to(device).view(-1, 784)
optimizer.zero_grad()
pred, q = model(data)
loss = compute_loss(pred, data, q)
loss.backward()
optimizer.step()
if iteration % print_freq == 0 or iteration == len(dataloader) - 1:
print('Epoch[{0}]({1} / {2}) - Loss: {3}'.format(
epoch + 1,
iteration + 1,
len(dataloader),
loss.item()
))
# sampling
z = torch.randint(0, n_classes, (batch_size, n_vars), device=device)
z = F.one_hot(z, n_classes).view(batch_size, -1)
x = model.decode(z.to(torch.float))
save_image(x.view(batch_size, 1, 28, 28), './data/sample_{0}.png'.format(epoch + 1))
아래는 학습한 decoder로 생성한 이미지입니다.
