포카전/카포전 2020 해킹 문제 출제
ctf , hacking , cryptography , reversing , assembly
서론
- 올해 정식 명칭은 포카전이기 때문에, 중립성을 위해 포카전/카포전으로 쓰겠습니다.
근 몇 년 간 포카전/카포전 해킹을 LeaveCat이라는 팀에서 출제하고 있습니다. 개인적으로 포항공대 PLUS의 후배들이 제 문제를 푸는 모습을 한 번 쯤 구경해보고 싶었기 때문에 이번에 LeaveCat의 일종의 멤버가 되어 처음으로 포카전/카포전 해킹 출제를 하게 되었습니다.
본래 과제로 최근에 개발하고 있던 웹사이트의 이야기를 이번 글에서 하려고 했지만, 출제진이 된 것이 일주일 전이었는데도 짧은 기간 동안 꽤 많은 시간을 투자해서 나름의 좋은 문제를 만들었다는 소기의 성과(?)를 얻었기 때문에 이번에 이렇게 글을 쓰게 되었습니다.
본론
총 3개의 문제를 만들었습니다.
- Baby Bubmi (0 solves)
- fixed point revenge (0 solves)
- simple_asm_reversing (0 solves)
모두 0 솔브인게 슬픕니다. 하지만 물어봤더니 인원수가 부족해 포스텍과 카이스트 양쪽 모두 다른 문제에 시간을 투자했다고 하더군요. 그나마 시간이 투자된 문제는 Baby Bubmi입니다.
Baby Bubmi (Crypto)
문제 이름은 적당한 문제 이름이 떠오르지 않은 상태에서 같은 팀의 다른 분이 Child Bubmi라는 문제를 만들고 있길래 채용했습니다. 하지만 Child Bubmi는 풀리고 이 문제는 풀리지 않았다는 점이 슬프네요.
문제의 concept는 Low-density attack의 extension이며, CryptoHack의 Real Eisenstein이라는 문제를 거의 그대로 차용했습니다.
#!/usr/bin/env python3
from decimal import *
import math
import random
import struct
from flag import flag
primes = [2]
for i in range(3, 100):
f = True
for j in primes:
if i * i < j:
break
if i % j == 0:
f = False
break
if f:
primes.append(i)
# Random shuffle the primes
# Now you cannot know the order
seed = struct.unpack('<i', flag[5:9])[0]
random.seed(seed)
random.shuffle(primes)
# Use ln function
# Now you cannot know the key itself
getcontext().prec = 100
keys = []
for i in range(len(flag)):
keys.append(Decimal(primes[i]).ln())
# Sum values
# Now you cannot know the flag
sum_ = Decimal(0.0)
for i, c in enumerate(flag):
sum_ += c * Decimal(keys[i])
ct = math.floor(sum_ * 2 ** 256)
print(ct)
코드의 구성은 다음과 같습니다.
- 100까지의 소수를 구한다. (총 25개)
- flag의 6번째에서 9번째까지의 byte를 random seed로 사용, 소수 array를 shuffle한다.
- shuffle한 각 소수들을 Decimal을 통해서 ln값을 표현한다. Decimal의 precision은 100이다.
- 소수의 ln값들과 flag의 각 byte를 곱한 값을 모두 합한다. 이에
2 ** 256을 곱한 뒤 내림한 값이 주어진다.
문제에서 주어진 ct 값은 737384863737803670841307970259513146291422299366557325168325233349136771464845311 입니다.
만약 기존에 CTF를 뛰면서 Knapsack Cryptosystem에 대해서 공부해보신 적이 있다면 익숙한 문제입니다. Knapsack Cryptosystem은 0/1 Knapsack 문제를 사용해서 만든 공개키 암호 시스템인데, 이에 대한 유명한 공격 방법 중 하나가 Low-density attack입니다.
Low-density attack를 설명하자면 다음과 같습니다.
- 총 $n$ 개의 수가 주어진 0/1 Knapsack 문제를 생각하자. 수 $a_1, a_2, \cdots, a_n$중 가장 큰 수 $\max_i a_i$에 대해, $d = n / \log_2 \max_i a_i$를 density라고 정의한다. 이 density가 충분히 작다면, Lenstra–Lenstra–Lovász(LLL) algorithm을 통해서 0/1 knapsack 문제를 항상 풀어낼 수 있다.
즉, 수의 개수에 비해서 가장 큰 수의 값이 현저히 작다면, LLL algorithm이라는 알고리즘을 통해서 풀어낼 수 있다는 것입니다. 이에 대해서 자세히 설명하고 있는 것이 Low-Density Attack Revisted(Link) 라는 paper입니다. 이 paper에서 소개하고 있는 알고리즘과 풀어낼 수 있는 density를 살펴보면, CTF에서 일반적으로 사용되는 LO algorithm은 0.6463 미만의 density에 대해서 동작하며, 이를 improve한 CJLOSS algorithm은 0.9408 미만의 density에 대해서 동작합니다.
LO algorithm은 LLL algorithm에 다음과 같은 $(n+1) \times (n+1)$ matrix를 넣습니다. ($s$는 0/1 knapsack 문제의 target value입니다.)
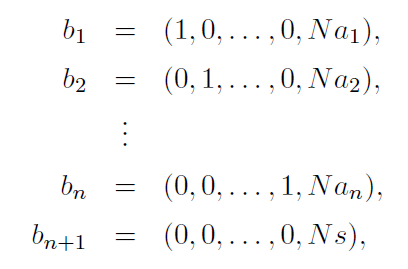
그리고 CJLOSS algorithm은 $b’_{n+1} = (1/2, 1/2, \cdots, 1/2, Ns)$를 사용합니다. 단순히 마지막 row를 0에서 $1/2$로 바꿨을 뿐인데 가능한 density의 범위가 거의 1.5배 가까이로 바뀐다는 것이 인상깊은 점입니다.
이 때 이 문제는 0/1 knapsack이 아니라 0~127 knapsack이라고 보는 것이 맞을 것입니다. Flag는 실제로 입력 가능한 값들일 것이므로 128 이상일 리가 없기 때문에, 0~127로 바운더리를 잡았습니다. 이 때 CJLOSS algorithm을 응용하기 위해서는 $1/2$ 대신 0과 127의 중간값인 64를 넣으면 잘 동작하게 됩니다. 또한 Knapsack에서 수 $a_1, a_2, \cdots, a_n$의 순서가 상관 없다는 것은 잘 알고 계실 것입니다. (다만 이 문제에서는 flag의 글자 순서가 바뀌어서 나올 것입니다.) 그러므로 primes의 순서는 우선 가능한 flag 값들을 구한 뒤 나중에 정합니다.
이를 바탕으로 sage 코드를 다음과 같이 작성했습니다. f 함수가 입력 N을 받은 뒤, 모든 수를 N으로 나누는 것을 볼 수 있습니다. 이는 실제로 2 ** 256를 곱해서 오차가 이미 발생한 상태이므로, 다양한 오차에 대해서 실험해보기 위해서 시도한 것입니다.
import math
from decimal import *
import random
import struct
getcontext().prec = int(100)
primes = [2]
for i in range(3, 100):
f = True
for j in primes:
if i * i < j:
break
if i % j == 0:
f = False
break
if f:
primes.append(i)
keys = []
for i in range(len(primes)):
keys.append(Decimal(int(primes[i])).ln())
arr = []
for v in keys:
arr.append(int(v * int(16) ** int(64)))
ct = 737384863737803670841307970259513146291422299366557325168325233349136771464845311
def encrypt(res):
h = Decimal(int(0))
for i in range(len(keys)):
h += res[i] * keys[i]
ct = int(h * int(16)**int(64))
return ct
def f(N):
ln = len(arr)
A = Matrix(ZZ, ln + 1, ln + 1)
for i in range(ln):
A[i, i] = 1
A[i, ln] = arr[i] // N
A[ln, i] = 64
A[ln, ln] = ct // N
res = A.LLL()
for i in range(ln + 1):
flag = True
for j in range(ln):
if -64 <= res[i][j] < 64:
continue
flag = False
break
if flag:
vec = [int(v + 64) for v in res[i][:-1]]
ret = encrypt(vec)
if ret == ct:
print(N, bytes(vec))
else:
print("NO", ret, bytes(vec))
for i in range(2, 10000):
print(i)
f(i)
실행한 결과는 다음과 같습니다.
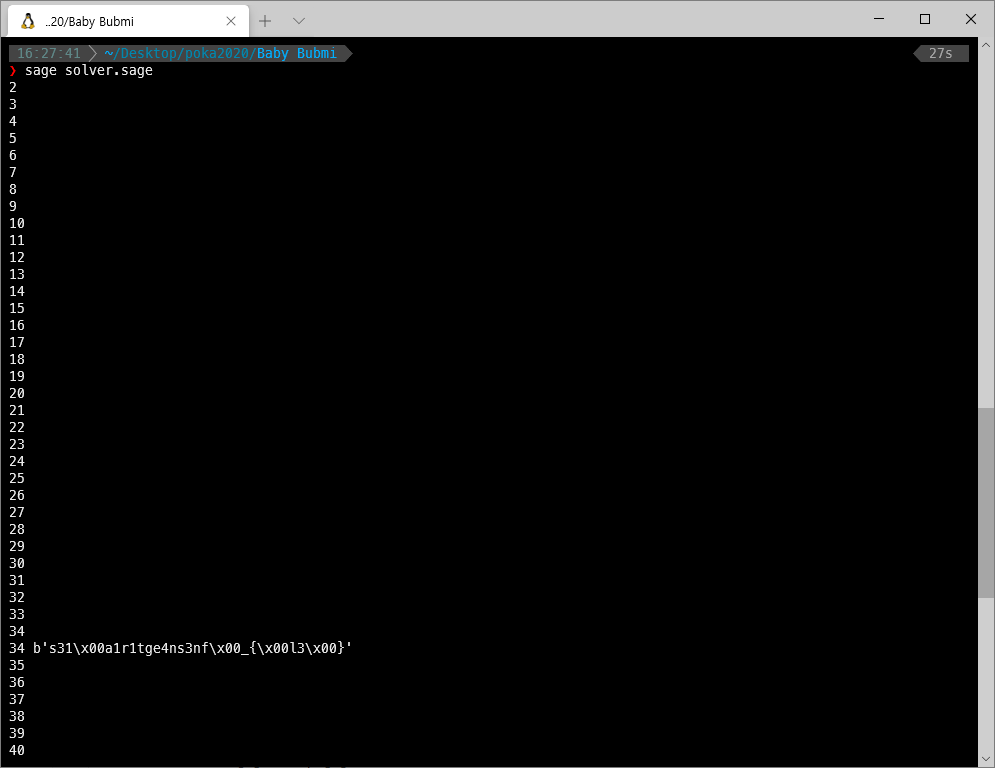
살펴보면 글자의 종류수가 그렇게 많지 않기 때문에, 위에서 primes를 shuffle할 때 사용했던 random seed의 값 후보도 그렇게 많지 않습니다. 이제 해당 값 후보들을 통해서 다시 flag를 shuffle한 뒤 정상적으로 flag{}로 시작하는 값을 찾아내면 됩니다.
import itertools
import random
import struct
shuffled = b's31\x00a1r1tge4ns3nf\x00_{\x00l3\x00}'
chars = list(set(shuffled) - set([0]))
for x in itertools.product(chars, repeat=4):
seed = struct.unpack('<i', bytes(x))[0]
random.seed(seed)
arr = [i for i in range(25)]
random.shuffle(arr)
flag = [0 for _ in range(25)]
for i in range(25):
flag[i] = shuffled[arr[i]]
flag = bytes(flag)
if flag.startswith(b'flag{'):
print(flag)
# break

Flag는 flag{r341_e1s3nst13n} 이며, 이는 CryptoHack의 Real Eisenstein 문제를 암시합니다.
fixed point revenge (Crypto)
과거에 0CTF에 fixed point라는 문제가 나온 적이 있습니다. 이 문제에서 쓰인 CRC, 그리고 GF에 대한 설명은 이전 블로그 글인 Understanding CRC에서 확인하실 수 있습니다.
fixed point 문제가 묻는 것은 CTF{x}의 CRC값이 x 가 되는 x값이었습니다. 이 문제에서는 이를 extension하고자 했습니다.
#!/usr/bin/env python3
from binascii import unhexlify
def crc64(x):
crc = 0
x += b'\x00' * 8
for c in x:
crc ^= c
for i in range(8):
if crc & (1 << 63) == 0:
crc = crc << 1
else:
crc = crc << 1
crc = crc & 0xFFFFFFFFFFFFFFFF
crc = crc ^ 0xd39d6612f6bcad3f
ret = []
for i in range(8):
ret.append(crc & 255)
crc >>= 8
return bytes(ret[::-1])
inp_hex = input("> ")
inp = unhexlify(inp_hex)
assert len(inp) == 8, "Hey, check the length"
def f(s):
ret = []
for c in s:
ret.append(inp[int(c)])
return bytes(ret)
def g(t, s):
return t + b"{" + f(s) + b"}"
def xor(a, b):
return bytes([c1 ^ c2 for c1, c2 in zip(a, b)])
constraints = [
[b"rbtree", "01234567", "12345670", b'\x36\xb0\x16\xf7\x5f\x42\xa9\xf6'],
[b"mathboy7", "12345670", "23456701", b'\x36\x94\xe4\xfc\x56\x1b\x9a\x5d'],
[b"rubiya", "23456701", "34567012", b'\xa8\xd8\x3a\xd2\x8d\x13\x4b\x16'],
[b"bincat", "34567012", "45670123", b'\xfc\x7f\xcc\xbe\xf9\xbc\x1b\xf6'],
[b"5unkn0wn", "45670123", "56701234", b'\x08\xea\xb4\xc6\xc3\x3e\x12\x4f'],
[b"saika", "56701234", "67012345", b'\x68\x0c\xe0\x7e\x6f\xa7\xe4\x36'],
[b"juno", "67012345", "70123456", b'\x18\x7e\x80\xb9\x54\x7b\x35\xa7'],
[b"wooeng", "01234567", "76543210", b'\xc1\x5b\xe0\x2f\x1b\xf8\xb3\xaf']
]
for person, input_order, output_order, const in constraints:
assert xor(crc64(g(person, input_order)), f(output_order)) == const, "WRONG :("
print("ERAI!")
print("Here's your flag")
print("flag{" + inp_hex + "}")
살펴보면 input으로 총 8byte를 받고, constraints가 총 8개가 주어집니다. 각 constraint의 의미는 다음과 같습니다.
- $s$, $a_0, \ldots, a_7$, $b_0, \ldots, b_7$, $v$가 주어졌을 때, $\text{CRC64}(s{input_{a_0}input_{a_1}\ldots input_{a_7}}) = input_{b_0}input_{b_1}\ldots input_{b_7} \oplus v$이여야 한다.
XOR($\oplus$)는 $\text{GF}(2^{64})$ 상에서 덧셈을 의미하므로, 해당 문제는 $input_0$부터 $input_7$까지 총 8개의 변수가 주어졌을 때 8개의 변수에 대한 8개의 linear equation을 주는 문제임을 알 수 있습니다.
sage를 통해서 각 식에서 $input_0, input_1, \ldots, input_7$의 계수를 구하는 코드를 작성해봅시다.
F.<x> = PolynomialRing(GF(2))
F.<x> = GF(2^64, modulus=x^64 + x^63 + x^62 + x^60 + x^57 + x^56 + x^55 + x^52 + x^51 + x^50 + x^48 + x^46 + x^45 + x^42 + x^41 + x^36 + x^33 + x^31 + x^30 + x^29 + x^28 + x^26 + x^25 + x^23 + x^21 + x^20 + x^19 + x^18 + x^15 + x^13 + x^11 + x^10 + x^8 + x^5 + x^4 + x^3 + x^2 + x + 1)
a = [ x^(8*i + 80) for i in reversed(range(8)) ]
b = [ x^(8*i) for i in reversed(range(8)) ]
row = [ a[i] + b[(i - 1) % 8] for i in range(8) ]
mat = [ row[-i:] + row[:-i] for i in range(7) ]
# Last row is different
b = [ x^(8*i) for i in range(8) ]
row = [ a[i] + b[i % 8] for i in range(8) ]
mat += [ row ] # 8x8 matrix!
CRC 자체가 각 변수에 대해서 $2^{80}$을 곱하는 효과만을 가지게 됩니다. 또한 이전의 글에 따라서 해당 linear equation의 상수는 $\text{CRC64}(s{ \backslash x00\backslash x00 … \backslash x00 }) + v$ 임을 알 수 있습니다. 이는 input에 그냥 0을 넣었을 때 나오는 constraint의 값을 살펴보면 됩니다.
우선 구한 matrix의 inverse를 Gaussian elimination을 통해 구해봅시다. $k \leq 8$인 $\text{GF}(2^k)$에 대해서는 sage가 inverse라는 함수를 통해서 자동으로 구해주지만, 이 경우는 그 범위를 넘어가기 때문에 직접 작성해줘야 합니다.
inv = [ [ 1 if i == j else 0 for i in range(8) ] for j in range(8) ]
for i in range(8):
factor = mat[i][i]
for j in range(8):
mat[i][j] /= factor
inv[i][j] /= factor
for j in range(i + 1, 8):
factor = mat[j][i]
for k in range(8):
mat[j][k] += mat[i][k] * factor
inv[j][k] += inv[i][k] * factor
for i in reversed(range(8)):
for j in range(i):
factor = mat[j][i]
for k in range(8):
mat[j][k] += mat[i][k] * factor
inv[j][k] += inv[i][k] * factor
이제 앞서 설명했던 것처럼 문제의 input에 0을 넣은 뒤 나온 상수 값을 통해서 flag를 구합니다. (0을 넣고 상수를 구한 과정은 생략했습니다.)
vector = [
F.fetch_int(0x1b043df67c053eeb),
F.fetch_int(0x6e68dc437c0b2a99),
F.fetch_int(0x8eabbe5ab86018bb),
F.fetch_int(0x7c3b54bc0b18bd3f),
F.fetch_int(0xf85907527add29da),
F.fetch_int(0x83c3e3323f2de05a),
F.fetch_int(0x05e50a9f33ce91eb),
F.fetch_int(0x1e7c73f6327d3beb)
]
s = ''
for i in range(8):
t = 0
for j in range(8):
t += inv[i][j] * vector[j]
s += format(t.integer_representation(), '02x')
print(s)
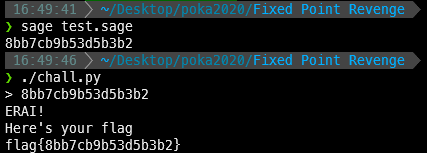
Flag는 flag{8bb7cb9b53d5b3b2} 입니다.
simple_asm_reversing (Reversing)
simple_asm_reversing은 assembly로 구성된 Reversing challenge 였습니다. 해당 프로그램은 input을 받은 뒤 여러 가지의 어셈블리 패턴을 수많이 반복한 후 register 4개 (rax, rbx, rsi, rdi)의 값을 주어진 상수 값과 비교해 같다면 올바른 input임을 알려주는 형태로 구성되어 있습니다. 이 때 이 어셈블리 패턴들은 모두 역연산이 손쉽게 가능하기 때문에, 주어진 상수 값으로부터 역연산을 통해 input을 구하는 것이 가능합니다.
문제를 만드는데 사용된 코드를 살펴보겠습니다. 우선 assembly template입니다. 중괄호로 감싸진 값들은 Python의 format에서 사용되는 부분입니다. 해당 template code는 InterKosen CTF 2020의 harmagedon이라는 문제를 참조해서 작성했습니다.
global _start
section .data
digstr db "Give me flag:"
congratzstr db "Congratz. that's the flag.",0xa
goodbyestr db "Try harder.",0xa
section .bss
inputbuf resb 33
section .text
_start:
mov rax, 1
mov rdi, 1
mov rsi, digstr
mov rdx, 13
syscall
mov rax, 0
mov rdi, 0
mov rsi, inputbuf
mov rdx, 33
syscall
mov rax, [inputbuf]
mov rbx, [inputbuf + 8]
mov rsi, [inputbuf + 16]
mov rdi, [inputbuf + 24]
{instructions}
mov rdx, {rax}
cmp rax, rdx
jne goodbye
mov rdx, {rbx}
cmp rbx, rdx
jne goodbye
mov rdx, {rsi}
cmp rsi, rdx
jne goodbye
mov rdx, {rdi}
cmp rdi, rdx
jne goodbye
congratz:
mov rax, 1
mov rdi, 1
mov rsi, congratzstr
mov rdx, 27
syscall
jmp e
goodbye:
mov rax, 1
mov rdi, 1
mov rsi, goodbyestr
mov rdx, 12
syscall
e:
mov rdi, 0
mov rax, 60
syscall
해당 코드를 읽어보면 input 32바이트를 받은 뒤 해당 바이트들을 rax, rbx, rsi, rdi에 넣고 {instructions}를 거친 뒤 값들을 {rax}, {rbx}, {rsi}, {rdi}와 비교하는 것을 알 수 있습니다.
해당 template assembly의 중괄호 부분을 대체하는 코드는 다음과 같이 작성되었습니다.
import struct
import random
flag = "flag{S0_x1mpl3_R3vERs1nG_isn7it}"
print(len(flag))
assert len(flag) == 32
with open('template.asm', 'r') as f:
data = f.read()
reg_dic = {
'rax': struct.unpack('<Q', flag[:8].encode())[0],
'rbx': struct.unpack('<Q', flag[8:16].encode())[0],
'rsi': struct.unpack('<Q', flag[16:24].encode())[0],
'rdi': struct.unpack('<Q', flag[24:].encode())[0]
}
instructions = ""
regs = ['rax', 'rbx', 'rsi', 'rdi']
bitmask = 0xFFFFFFFFFFFFFFFF
for i in range(400000):
choice = random.randint(1, 22)
random.shuffle(regs)
if choice == 1:
instructions += " add {}, {}\n".format(regs[0], regs[1])
reg_dic[regs[0]] += reg_dic[regs[1]]
reg_dic[regs[0]] &= bitmask
elif choice == 2:
val = random.getrandbits(31)
instructions += " add {}, {}\n".format(regs[0], hex(val))
reg_dic[regs[0]] += val
reg_dic[regs[0]] &= bitmask
# ... 생략
elif choice == 22:
val = random.getrandbits(31)
instructions += " clc\n adc {}, {}\n".format(regs[0], hex(val))
reg_dic[regs[0]] += val
reg_dic[regs[0]] &= bitmask
data = data.format(instructions=instructions,
rax = reg_dic['rax'],
rbx = reg_dic['rbx'],
rsi = reg_dic['rsi'],
rdi = reg_dic['rdi']
)
with open('chall.asm', 'w') as f:
f.write(data)
우선 flag를 고정한 뒤, flag로부터 rax, rbx, rsi, rdi의 초기값을 구합니다. 그리고 그 뒤로 40만개의 instruction 패턴들을 넣으면서, rax, rbx, rsi, rdi 값이 어떻게 바뀌는지 tracking합니다.
이 패턴들은 모두 역연산이 가능한 것들로 구성되어 있으며, 패턴에서 사용되는 register 들은 random.shuffle(regs)를 통해서 선택됩니다. 패턴들은 다음과 같이 총 22가지가 있습니다.
| 패턴 | 설명 |
|---|---|
add reg1, reg2 |
reg1에 reg2를 더합니다. |
add reg1, imm |
reg1에 imm를 더합니다. |
sub reg1, reg2 |
reg1에 reg2를 뺍니다. |
sub reg1, imm |
reg1에 imm을 뺍니다. |
xchg reg1, reg2 |
reg1과 reg2 값을 바꿉니다. |
mov rdx, imm, mul rdx |
rax에 imm을 곱한 값의 lower 64-bit를 rax에 넣습니다. 이 때 imm은 홀수로 설정되기 때문에 항상 역연산이 가능합니다. |
xor reg1, reg2 |
reg1에 reg2를 xor합니다. |
xor reg1, imm |
reg1에 imm을 xor합니다. |
neg reg1 |
reg1에 2의 보수를 취합니다. |
inc reg1 |
reg1의 값을 1 증가시킵니다. |
dec reg1 |
reg1의 값을 1 감소시킵니다. |
lea reg1, [reg1 + reg2] |
reg1에 reg2를 더합니다. |
lea reg1, [reg1 + imm] |
reg1에 imm을 더합니다. |
nop |
아무것도 하지 않습니다. |
not reg1 |
reg1에 1의 보수를 취합니다. |
rol reg1, imm |
reg1을 imm만큼 left rotation shift를 취합니다. |
ror reg1, imm |
reg1을 imm만큼 right rotation shift를 취합니다. |
stc, adc reg1, reg2 |
stc는 carry bit를 set하고, adc는 carry bit가 있을시 1을 더 더합니다. 즉, reg1에 reg2 + 1을 더합니다. |
clc, adc reg1, reg2 |
clc는 carry bit를 unset합니다. 곧 reg1에 reg2만 더합니다. |
stc, adc reg1, imm |
reg1에 imm + 1을 더합니다. |
clc, adc reg1, imm |
reg1에 imm을 더합니다. |
해당 패턴들을 잘 파싱하는 코드를 짠 뒤 역연산을 하는 것이 문제의 의도였는데, 시간이 부족해서 파싱한 뒤 풀어내는 솔버까지 작성하지는 못했습니다. 만약 문제를 본 사람이 있다면 의도를 빠르게 파악하고 코딩하지 않았을까 생각합니다.
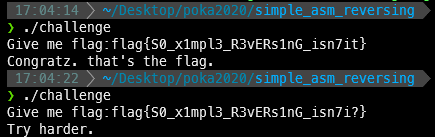
Flag는 flag{S0_x1mpl3_R3vERs1nG_isn7it} 입니다.
결론
안타깝게도 Baby Bubmi를 제외하고는 어떠한 문제도 다른 사람들이 풀려고 보지조차 않았습니다. 정말 슬픈 일이 아닐 수 없습니다. Baby Bubmi의 경우 GoN에서 대회가 끝나기 5분 전에 shuffle된 flag까지는 구했으나, 그 뒤 shuffle된 flag를 복구하는 코드를 짤 시간이 없어서 풀지 못했다는 이야기를 듣고 정말 아쉽다고 생각했습니다.
문제의 퀄리티가 스스로 생각하기에도 나쁘지 않기에, 대회가 끝난 이후 꼭 PLUS나 GoN에서 풀어봤으면 하는 바람이 있습니다. 다음에는 어떻게 아이디어를 improve해서 문제를 만들지 미리 고민해두어야겠다고 생각했습니다.