양자 컴퓨팅 - Surface Code
최근 양자 컴퓨팅의 error detection 및 correction에 사용되는 surface code의 기초를 잘 설명한 논문인 Surface codes: Towards practical large-scale quantum computation을 접했습니다. 이 포스트를 통해 양자 컴퓨팅에서 어떻게 error detection을 진행하고, surface code가 어떤 개념인지 설명하고자 합니다.
배경 지식
Shor’s Algorithm이나 Grover’s Algorithm 등의 양자 알고리즘이 개발되며 양자 컴퓨팅에 대한 관심이 커졌습니다. 2020년 현재 IBM Q Experience나 Amazon Braket, Microsoft QDK 등으로 양자 컴퓨팅 프로그래밍 언어를 사용할 수도 있습니다. 그러나 이런 시스템이 물리적인 양자 체계와 연결되어 있는 경우는 매우 드뭅니다. Microsoft Q# 코드를 실행한다고 해서 이에 해당되는 qubit이 실제로 생성되지는 않기 때문입니다.
Surface code는 물리적 큐빗(양자)을 프로그램으로 제어 가능한 논리적 큐빗으로 다루는 구조입니다. 각 연산에 대한 오류 가능성은 잘 모르겠지만 surface code가 상당히 허용 범위가 넓어 보입니다. 하지만 이 비율을 만족하기 위해 엄청나게 많은 물리적 큐빗이 필요합니다. 합리적인 수준의 오류가 나는 논리적 큐빗 1개를 만들기 위해 surface code로 $10^3$개에서 $10^4$개의 물리적 큐빗이 필요합니다. 어느 정도 기능이 하는 프로그램을 만드려면 못해도 $10^8$개의 큐빗이 필요합니다. 이에 대한 자세한 수학적 계산법은 잘 모르지만, 양자 컴퓨팅에서 큐빗 오류가 그리 자비롭지 않다는 지표로만 이해하면 되지 않을까 싶습니다.
개요
양자 컴퓨터의 기본을 이루는 큐빗의 상태와 연산자입니다.
기저 상태이자 $\hat{Z}$축인
$\left\vert{g}\right> = \begin{bmatrix} 1 \ 0 \end{bmatrix}$
가 있으며, 들뜬 상태인
$\left\vert{e}\right> = \begin{bmatrix} 0 \ 1 \end{bmatrix}$
가 다른 축을 이룹니다. $\hat{Z}$ 연산자는 다음과 같이
$$\hat{Z} = \hat{\sigma_z} = \begin{bmatrix}
1 & 0
0 & -1
\end{bmatrix}$
정의되며 고윳값은 $+1$, $-1$을 가지고 고유벡터 $\left\vert{g}\right>$, $\left\vert{e}\right>$를 가집니다.
$\hat{X}$ 연산자는 다음과 같이
$$\hat{X} = \hat{\sigma_x} = \begin{bmatrix}
0 & 1
1 & 0
\end{bmatrix}$
정의되며 고윳값 $+1$ , $-1$ 및 고유벡터
$$\begin{align}
\left\vert{+}\right> &= \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \ 1 \end{bmatrix} = \frac{1}{\sqrt{2}}(\left\vert{g}\right> + \left\vert{e}\right>)
\left\vert{-}\right> &= \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \ -1 \end{bmatrix} = \frac{1}{\sqrt{2}}(\left\vert{g}\right> - \left\vert{e}\right>)
\end{align}$
를 가집니다.
$\hat{Y}$ 연산자는 다음과 같이
$$\hat{Y} = -i\hat{\sigma_y} = \hat{Z}\hat{X} = \begin{bmatrix}
0 & 1
-1 & 0
\end{bmatrix}$
로 정의되며, 허수가 들어가는 $\hat{\sigma}_y$랑은 다릅니다.
$\hat{X}$, $\hat{Y}$, $\hat{Z}$ 연산자는 다음을 만족합니다.
$\begin{align}\hat{X}\,^2 &= -\hat{Y}\,^2 = \hat{Z}\,^2 = I \ \hat{X}\hat{Z} &= -\hat{Z}\hat{X} \ [\hat{X},\hat{Y}] &= \hat{X}\hat{Y} - \hat{Y}\hat{X} = -2\hat{Z}\end{align}$
양자 상태에서 관측이란, 어떤 양자 상태를 관측과 관련된 연산자의 고유벡터로 사영하는 과정입니다. 때문에 $M_Z$를 거친 큐빗은 $\pm \left\vert{g}\right>$나 $\pm \left\vert{e}\right>$이 됩니다.
이런 연산자들이 왜 필요할까요? Solovay–Kitaev theorem에 의해 임의의 양자 회로가 ‘적당히’ 짧고, universial set으로만 이루어진 양자 회로의 곱으로 근사될 수 있기 때문입니다. 하드웨어 구현상 universial set으로는 Clifford + T gate set이 종종 사용됩니다.
Single-qubit Error
bit error는 0이 1이 되거나, 1이 0이 되어 뒤집히는 현상입니다. qubit error도 비슷하게 $\hat{X}$나 $\hat{Z}$가 뒤집히는 (한 번 더 곱해진) 현상입니다. $\hat{X}^2 = \hat{Z}^2 = I$이기 때문에 오류를 감지하기만 해도 정정을 할 수 있습니다. 그러므로 어떻게 하면 큐빗의 상태를 감지할 지가 문제입니다.
$M_X$와 $M_Z$를 통해, 각 양자 상태를 확실히 관측해볼 수도 있습니다. 그러나 $\hat{X}\hat{Z} \neq \hat{Z}\hat{X}$이기 때문에 $M_X$와 $M_Z$는 독립적이지 않습니다. 한쪽으로 관측을 하면 양자 정보가 소실됩니다. 흥미롭게도, 큐빗을 2개 ($a$와 $b$) 준비한 다음 $\hat{X}_a\hat{X}_b$와 $\hat{Z}_a\hat{Z}_b$를 연산자로 삼으면 교환법칙이 성립합니다.
$\begin{align}[\hat{X}_a\hat{X}_b, \hat{Z}_a\hat{Z}_b] &= (\hat{X}_a\hat{X}_b)(\hat{Z}_a\hat{Z}_b) - (\hat{Z}_a\hat{Z}_b)(\hat{X}_a\hat{X}_b) \ &= \hat{X}_a\hat{Z}_a\hat{X}_b\hat{Z}_b - \hat{Z}_a\hat{X}_a\hat{Z}_b\hat{X}_b \ &= (-\hat{Z}_a\hat{X}_a)(-\hat{Z}_b\hat{X}_b) - (\hat{Z}_a\hat{X}_a)(\hat{Z}_b\hat{X}_b) \ &= \hat{0}\end{align}$
교환법칙이 성립하기 때문에, 두 연산자를 기저로 삼을 수도 있습니다. 그리고 $\hat{X}_a\hat{X}_b$로도, $\hat{Z}_a\hat{Z}_b$로도 관측해도 변하지 않는 양자 상태들이 존재합니다.
| $\hat{Z}_A\hat{Z}_b$ | $\hat{X}_A\hat{X}_b$ | $\left\vert{\psi}\right>$ |
|---|---|---|
| $ +1 $ | $ +1 $ | $(\left\vert{gg}\right> + \left\vert{ee}\right>)/\sqrt{2}$ |
| $ +1 $ | $ -1 $ | $(\left\vert{gg}\right> - \left\vert{ee}\right>)/\sqrt{2}$ |
| $ -1 $ | $ +1 $ | $(\left\vert{ge}\right> + \left\vert{eg}\right>)/\sqrt{2}$ |
| $ -1 $ | $ -1 $ | $(\left\vert{ge}\right> - \left\vert{eg}\right>)/\sqrt{2}$ |
예를 들어 $\left\vert{\psi}\right> = (\left\vert{gg}\right> - \left\vert{ee}\right>)/\sqrt{2}$이면 $\hat{Z}_a\hat{Z}_b \left\vert{\psi}\right> = \left\vert{\psi}\right>$이고, $\hat{X}_a\hat{X}_b \left\vert{\psi}\right> = -\left\vert{\psi}\right>$이 성립합니다. 때문에 $\left\vert{\psi}\right>$는 두 연산자로 관측을 해도 바뀌지 않고, 양자 상태가 소실되지도 않습니다! 그렇기 때문에 error detection에 사용될 수 있습니다. 이런 특성을 지닌 연산자 쌍을 stabilizer라고 부릅니다.
Surface Code
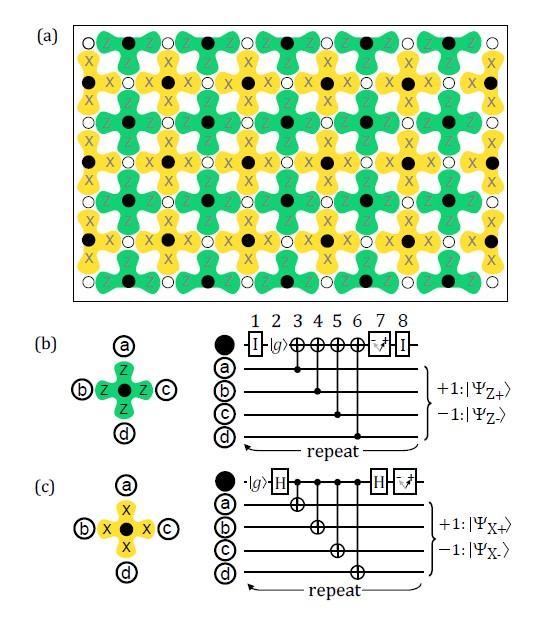
Surface code는 다음과 같이 생겼습니다.
흰 동그라미는 data qubit으로, 양자 상태가 저장됩니다. 검은 동그라미는 measurement qubit으로, data qubit에 변형을 가할 때 사용됩니다. 이 큐빗이 물리적으로 수행할 수 있는 연산들도 정해져 있지만 (초기화, 큐빗 회전, CNOT 등등) 자세한 설명은 생략합니다.
measurement qubit은 두 종류로 나뉩니다. measure-Z라고 불리는 노란색 공간의 큐빗과 measure-X라고 불리는 초록색 공간의 큐빗입니다. 각 data qubit은 2개의 measure-X 큐빗과 measure-Z 큐빗과 연결되어 있고, 각 measurement qubit은 4개의 data qubit과 연결되어 있습니다.
measurement qubit은 $\hat{X}$/$\hat{Z}$ stabilizer인 $\hat{X}_a\hat{X}_b\hat{X}_c\hat{X}_d$/$\hat{Z}_a\hat{Z}_b\hat{Z}_c\hat{Z}_d$를 data qubit에 적용할 수 있습니다. 이 연산도 아까 전 큐빗 2개일 때의 $\hat{X}_a\hat{X}_b$/$\hat{Z}_a\hat{Z}_b$처럼 서로 교환법칙이 성립할 뿐더러, data qubit의 상태가 $\left\vert \psi \right>$일 때
$\hat{X}a\hat{X}_b\hat{X}_c\hat{X}_d \left\vert \psi \right> = X{abcd}\left\vert {\psi} \right>$
가 성립합니다. $\hat{Z}$ stabilizer도 마찬가지입니다.
각 stabilizer는 0개 또는 2개의 data qubit을 공유합니다. 공유하는 data qubit이 없으면 당연히 교환법칙이 성립하며, 2개를 공유할 때는 stabilizer의 타입이 같으면 자명하게 성립하고, 다를 땐 위에서 살펴보았던 계산방식에 의해 성립합니다.
회로는 상대적으로 간단한 편입니다. $\hat{X}$ stabilizer는 CNOT을 각 data qubit에 걸어주고, $\hat{Z}$ stabilizer는 phase kickback trick을 이용해 data qubit에서 measurement qubit으로 CNOT을 걸어주며 $\hat{Z}$을 data qubit에 적용합니다. 그리고 관측이 끝나면 data qubit을 다시 원래대로 돌려놓기 위해 이 과정을 한 번 더 반복합니다.
Surface Code w/ Single-qubit Error
surface code에 나타날 수 있는 오류는 다음과 같이 4가지가 있습니다.
- $\hat{X}$ bit-flip error
- $\hat{Z}$ phase-flip error
- $\hat{Y} = \hat{Z}\hat{X}$ error
- $M$(measurement) error (관측 과정에서도 오류가 있을 수 있습니다)
이 오류들을 그림을 나타내면 다음과 같습니다. 세로로 시간별 surface code의 현황이 나옵니다.
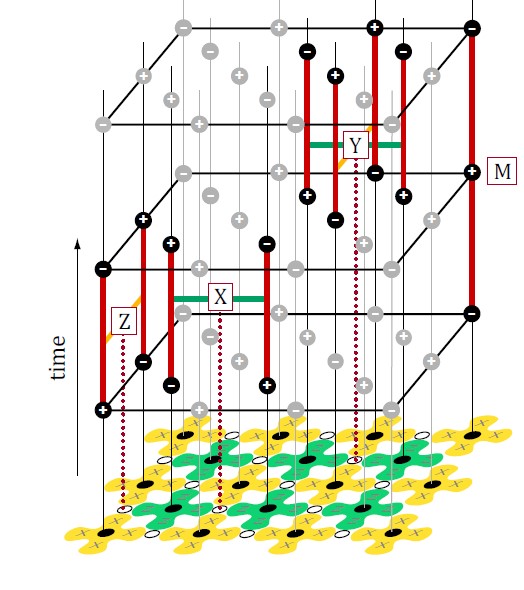
원래 큐빗의 상태가 $\left\vert \psi \right>$인데 $\hat{Z}_a$가 곱해져서 $\left\vert \psi’ \right> = \hat{Z}_a \left\vert \psi \right>$가 되었다고 합시다. 그러면
\[\begin{split} \hat{X}_a\hat{X}_b\hat{X}_c\hat{X}_d(\hat{Z}_a \left\vert{\psi}\right>) &= -\hat{Z}_a(\hat{X}_a\hat{X}_b\hat{X}_c\hat{X}_d\left\vert \psi \right>) \\ &= -\hat{Z}_aX_{abcd}\left\vert\psi\right> \end{split}\]가 성립하기 때문에 measure-X로 큐빗에 영향을 미치지 않고 부호를 통해 오류를 감지할 수 있습니다. 매우 당연하게도 measure-Z도 큐빗에 영향을 미치진 않지만, 곱한다고 해서 부호가 변경되진 않습니다. 비슷하게, $\hat{X}$ 오류도 measure-Z로 감지할 수 있습니다. $\hat{Y}$ 오류는 두 오류가 동시에 나타난 셈이므로, 독립적으로 감지할 수 있습니다.
감지되었다고 해서 양자 회로를 적용하기보다는 소프트웨어 차원에서 오류가 있음을 체크해서 알아서 부호를 뒤집는 방법이 낫습니다. 양자 회로를 적용하면 또 다른 오류가 나타날 가능성이 있기 때문입니다. 관측 오류는 여러 번 관측을 하며 극복해냅니다.
Logical Operator
신기하게도, surface code에는 data qubit 말고도 숨겨진 logical qubit이 존재합니다.
현재 다루고 있는 9 * 9 surface code는 data qubit이 41개, measurement qubit이 40개입니다. 각 data qubit은 2 * 41개의 자유도를 가지고 있고 (Bloch sphere를 생각하면 임의의 큐빗은 3차원 극좌표계 $(\theta, \phi)$로 나타낼 수 있습니다), measurement qubit은 독립적인 2 * 40개의 제약조건을 추가합니다. 그럼 2개의 제약되지 않은 자유도가 남는데, 어떻게 조작할 수 있을까요?
수학적으로 살펴봅시다. 한 data qubit에 $X$ 연산을 하면 이와 인접한 $\hat{Z}$ stabilizer (measurement) 큐빗에만 영향을 줍니다. 여기서 ‘영향을 준다’는 뜻은 교환법칙이 성질하지 않아 큐빗의 정보가 흐트러짐을 의미합니다. 기본적으로 $X$ 연산끼리는 교환법칙이 성립하니 영향을 주지 않습니다. 그러면 $\hat{Z}$ stabilizer 에 영향을 주는 마주보는 또다른 큐빗에 $X$ 연산을 하면 stabilizer의 연산에 영향을 주지 않습니다.
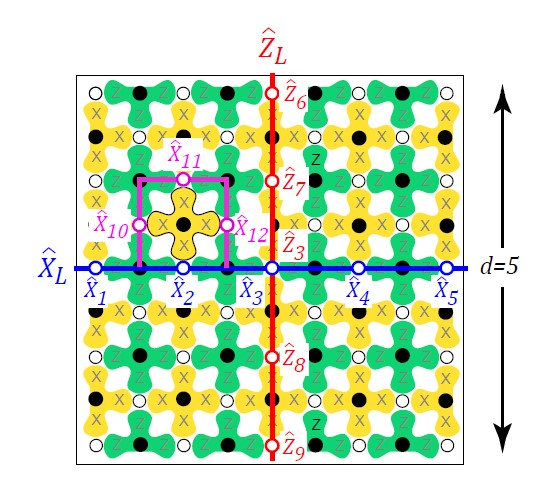
그렇기 때문에 수학적으로 $\hat{X}_L = \hat{X}_1\hat{X}_2\hat{X}_3\hat{X}_4\hat{X}_5$는 그 어떤 stabilizer의 측정 결과에도 영향을 미치지 않습니다. 사이의 $\hat{Z}$ stabilizer는 두 개의 $\hat{X}$에 끼워져있기 때문입니다. 그렇기 때문에 기존의 큐빗의 상태가 $\left\vert \psi \right>$이라 하면 새로운 상태 $\left\vert \psi_X \right> = \hat{X}_L\left\vert \psi_X \right>$는 $\left\vert \psi \right>$는 아니지만 surface code의 stabilizer로 관측하면 $\left\vert \psi \right>$가 나옵니다. $\hat{X}_L$이 모든 stabilizer와 독립이기 때문에 (교환법칙이 성립하기 때문에) 그렇습니다. 덕분에 제약되지 않았던 하나의 자유도를 조절할 수 있게 되었습니다.
비슷하게, $\hat{Z}_L = \hat{Z}_6\hat{Z}_7\hat{Z}_3\hat{Z}_8\hat{Z}_9$은 다른 하나의 자유도를 조절할 수 있습니다. 그리고 수학적으로 그 외의 제약되지 않은 자유도는 없음을 보일 수 있습니다. 그러므로 data qubit의 상태는 $\left\vert Q \right> \left\vert q_L \right>$로 쓸 수 있습니다. $\left\vert Q \right>$는 40개의 stabilizer로 조절할 수 있는 $2^{40}$ 차원의 힐베르트 공간의 벡터이며, $\left\vert q_L \right>$은 제약되지 않은 자유도를 다루는 2차원 힐베르트 공간의 벡터입니다.
결론
그 뒤로는 실제 오류를 어떻게 검출하고 비율은 어떻게 되는지, 어떻게 surface code에 더 많은 logical qubit을 만드는지, 양자 회로는 어떻게 구성하는지가 서술되어 있습니다. 양자 컴퓨팅이 오류 측면에서 실용화가 되려면 소프트웨어, 알고리즘, 하드웨어, 물리적 큐빗 등 수많은 분야의 발전이 필요해 보입니다. 양자 컴퓨팅에서의 오류는 깊게 생각해보진 않았는데 덕분에 더 넓은 시야를 얻을 수 있었습니다.