공개 키 암호화 시스템과 수학적 안전성
이 글에서는 공개 키 암호화 시스템이 발전해나가면서 같이 논의된 수학적 개념을 살펴보고자 합니다. 특히, 암호문으로부터 평문을 알아낼 수 없다는 막연한 속성을 수학적으로 어떻게 표현하는지 알아보고자 합니다.
목차는 다음과 같습니다.
- 공개 키 암호화 시스템
- RSA 암호
- One-wayness CPA
- Semantic Security and Indistinguishability
- Random Oracle Model
- 마무리
- 각주
공개 키 암호화 시스템
공개 키 암호화 시스템Public Key Cryptosystem, PKC은 W. Diffie와 M. E. Hellman의 1976년 논문 ‘New Directions in Cryptography’1에 처음 등장합니다. 이 때까지만 해도 모든 암호는 DES 같이 대칭 키 암호화 시스템에 기반했습니다. 때문에 고질적인 약점인 privacy를 해결하기 어려웠습니다. 때문에, 논문의 3장에서 공개 키 암호화 시스템과 공개 키 분배를 제안해 처음 연결된 두 사람끼리 도청 가능한 환경에서 비밀키를 나누어 가질 수 있는 방법을 제안합니다Diffie-Hellman key exchange. 다만, 실제 공개 키 암호화 시스템의 예시를 들지는 못했습니다.
또 다른 문제는 인증authentication으로, 기초적인 전자 서명의 아이디어를 4장에서 제시합니다. 그리고 임의의 공개 키 암호화 시스템을 단방향 인증 시스템으로 바꿀 수 있음을 보입니다. 5장에서는 다양한 암호학 문제를 논의합니다. 6장에서는 시간 복잡도 이론을 통해 암호학에 대한 논의를 진행합니다.
배경 지식
이론적으로 무한한 시간이 주어져도 평문에 대해 조금의 정보라도 알아낼 수 없는 성질인 perfect secrecy를 만족하는 암호화 방식인 one-time pad가 존재합니다. 하지만, 보내고자 하는 평문 이상의 길이를 지닌 key를 한 번만 사용하고 폐기해야 하기 때문에 실용성이 떨어집니다. 때문에 암호학자들은 다항 시간 안에 평문을 알아낼 수 없는 시스템을 논의하게 됩니다. 논문에서는 computationally infeasible하다고 표현합니다.
공격자의 모델도 다양한데, 논문에서는 3가지가 소개됩니다.
- ciphertext only attackCOA : 공격자가 암호문만 가지고 있습니다.
- known plaintext attackKPA : 공격자가 몇 개의 (평문, 암호문) 쌍을 가지고 있습니다.
- chosen plaintext attackCPA : 공격자는 임의의 평문에 대한 암호문을 계산할 수 있습니다.
나중에 한 종류가 더 추가됩니다.
- chosen ciphertext attackCCA : 공격자는 자신이 해독하고자 하는 암호문을 제외한 모든 암호문을 해독할 수 있습니다.
공개 키 암호화 시스템의 정의
공개 키 암호화 시스템은 두 함수집합
$$\begin{align}
{E_K}_{K \in {K}} &: {M} \to {M}
{D_K}_{K \in {K}} &: {M} \to {M}
\end{align}$
으로 정의됩니다. $\{M\}$은 평문의 상태공간으로 유한하며, $\{K\}$는 key의 상태공간입니다. 이 두 함수군은 다음 4가지 조건을 만족합니다.
- 임의의 $ K \in \{K\}$에 대해 $E_K$는 $D_K$의 역함수이다.
- 임의의 $ K \in \{K\}$과 $ M \in \{M\}$에 대해 $E_K(M)$와 $D_K(M)$은 쉽게 계산 가능하다.
- 거의 모든 $K \in \{K\}$에 대해, $E_K$로부터 $D_K$와 동치인 알고리즘을 효율적으로 이끌어낼 수 없다 (computationally infeasible).
- 임의의 $K \in \{K\}$에 대해, $(E_K, D_K)$를 효율적으로 이끌어낼 수 있다.
3번 성질 덕분에 암호화 함수 $E_K$는 외부에 공개해도 됩니다. 복호화 함수 $D_K$ 없이는 효율적으로 해독할 수 없기 때문입니다. 4번 성질 덕분에 $K$를 무작위로 골라도 $E_K$와 $D_K$를 어렵지 않게 생성해낼 수 있습니다.
Diffie-Hellman Key Exchange
비록 공개 키 암호화 시스템의 예시는 들지 못했지만, 뚫기 어려운 키 교환 시스템의 예시는 있습니다. 앞서 언급한 Diffie-Hellman Key Exchange는 유한체 $GF(p)$에서의 이산 대수 문제의 난이도를 이용합니다. 임의의 소수 $p$와 유한체 $GF(p)$의 생성자 $g$가 주어질 때, 임의의 $a \equiv g^\alpha \mod p$에 대해 $\alpha$를 계산하기 어렵기 때문입니다. 2
키 공유 과정은 다음과 같습니다. 전통에 따라 Alice와 Bob이 키를 공유하는 상황입니다.
- 소수 $p$와 $GF(p)$의 생성자 $g$는 모두에게 공개되어 있습니다.
- 소수 $p$에 대해 ${1, 2, \cdots, p-1}$ 사이에 있는 수 하나를 무작위로 뽑습니다. Alice는 $\alpha$, Bob은 $\beta$를 뽑았습니다.
- Alice는 Bob에게 $g^\alpha \mod p$를 보내고, Bob은 Alice에게 $g^\beta \mod p$를 보냅니다.
- 그럼 Alice와 Bob 둘 다 $g^{\alpha\beta} \mod p$를 계산할 수 있습니다.
- 이 과정을 누가 도청한다 해도 $(p, g, g^\alpha \mod p, g^\beta \mod p)$만 가지고는 $g^{\alpha\beta} \mod p$를 계산하기 어렵습니다.
이와 같이 $g^\alpha \mod p, g^\beta \mod p$만 가지고 $g^{\alpha\beta} \mod p$를 계산하는 문제를 Diffie-Hellman problem이라 부릅니다. 이산 로그 문제를 해결할 수 있으면 Diffie-Hellman problem을 해결할 수 있지만 그 역이 성립하는지는 밝혀지지 않았습니다.
엄밀히 따지자면, Diffie-Hellman key exchange는 수학적으로 계산이 어렵다고 증명된 문제는 아닙니다. 반증되지도 않았고 사람들이 연구해본 결과 어려워보이기에 안전하다고 여겨질 뿐입니다. 금방 나올 RSA도 동일한 문제점을 지닙니다.
그 외 전자서명 관련 내용은 생략하도록 하겠습니다.
RSA 암호
최초의 공개 키 암호화 시스템은 익히 알려진 RSA cryptosystem입니다. R. Rivest, A. Shamir, L. Adleman이 1977년에 최초로 MIT에서 연구하여 발표하고 1978년에 개정하여 발표하였습니다.3
RSA는 암호화 키로 $(e, n)$을 쓰고, 복호화 키로 $(d, n)$을 씁니다. 평문 $m$을 $0, 1, \cdots, n-1$ 중 하나로 표현할 수 있으면, 암호화는 $C \equiv M^e \mod n$이며 복호화는 $M \equiv C^d \mod n$입니다. 전제 조건으로 $n$은 두 소수 $p$와 $q$의 곱이며, $d$는 $\gcd(d, (p-1)\cdot(q-1)) = 1$을 만족하는 적당히 큰 정수입니다 ($\phi(n) = (p-1)\cdot(q-1)$). 그럼 $e$는 $e \cdot d \equiv 1 \mod (p-1)\cdot(q-1)$로 정의됩니다. 거꾸로 $e$를 먼저 생성하고 $d$를 찾을 수도 있습니다.
오일러 정리에 의해 $\gcd(M, n) = 1$이면 $M^{\phi(n)} \equiv 1 \mod n$ 이기 때문에 암호화 함수와 복호화 함수가 역함수 관계라는 1번 조건을 만족합니다. $M^e \mod n$이나 $C^d \mod n$은 거듭제곱을 이용해 효율적으로 계산할 수 있기 때문에 2번 조건도 만족합니다. 일반적으로 $(e, n)$에서 $d$나 $p$, $q$를 알아내는 과정은 어렵다고 여겨지기에 3번 조건도 만족합니다. 마지막으로 4번 조건은 키 생성과 관련되어 있습니다. 큰 소수는 어렵지 않게 찾을 수 있습니다. 소수 정리에 의해 자연수 $n$이 소수일 확률은 $\frac{1}{\ln n}$이며, 소수 판정은 Miller-Rabin 등의 확률적 알고리즘으로 빠르게 할 수 있기 때문입니다. $d$도 $\max(p, q)$보다 큰 소수를 고르면 되므로 생성이 어렵지 않습니다.
그러므로 RSA는 공개 키 암호화 시스템임을 알 수 있습니다. 논문에서 이를 이용해 전자서명을 어떻게 진행하면 되는지도 서술되어 있습니다. 지금까지도 사용되며 공개 키 암호화 시스템의 대표주자입니다.
특정 전제 조건 하에서 RSA를 파훼하는 있으며, RSA 암호화 기법은 $n$의 소인수분해로 환원되지만 그 역은 보여지지 않았습니다. 때문에 소인수분해 문제보다 더 쉬울 수도 있습니다. 실제로 Coppersmith’s attack이나 Wiener’s attack 같이 특정 조건 하에서 RSA를 파훼할 수 있는 공격 기법도 있으며, 소수 $p$나 $q$도 안전한 관계에 있지 않으면 Pollard’s p-1 algorithm 등으로 파훼될 수 있습니다. $e$는 보통 $65537 = 2^{16} + 1$이지만 3이나 1을 사용하는 소프트웨어도 있습니다. Bleichenbacher’s attack은 잘못 구현된 RSA에서 임의의 RSA 서명 위조할 수 있는 기법입니다. 수십 년간 사용되면서도 일반적인 파훼법이 나오지 않았고, 최초의 공개 키 암호화 시스템이라는 이름값이 있기에 오늘날까지 사용되고 있긴 합니다. 그러나 TLS 1.3의 암호화 기법에서 제거하자는 논의도 있었고, 점차 많은 프로젝트가 RSA 대신 다른 암호화 기법을 사용하는 추세입니다.
One-wayness CPA
그럼 수학적으로 파훼가 어려운 암호화 시스템을 어떻게 정의할 수 있을까요? 여기서 one-wayness property가 나옵니다. 공개된 정보만을 가지고 공격자가 다항 시간 내에 공격이 성공할 확률이 negligible할 때 one-wayness property를 만족한다고 합니다. negligible한 함수 $\mu(x)$는 임의의 양의 정수 $c$에 대해 $x_c \in \mathbb{N}$이 존재해 $x > x_c \implies \left \vert \mu(x) \right \vert < \frac{1}{x^c}$를 만족합니다. 암호학 관점에서 볼 때 말 그대로 무시 가능한 수준의 함수입니다.
one-wayness property를 만족하고 chosen plaintext attack에 안전한 공개 키 암호화 시스템을 OW-CPA를 만족한다고 합니다. 예시로 Rabin cryptosystem이 있습니다. Rabin cryptosystem과 소인수분해 문제는 서로 환원되기 때문에, Rabin cryptosystem을 (CPA 상에서) 파훼하려면 소인수분해 문제를 해결해야 합니다.
Semantic Security and Indistinguishability
One-wayness는 암호문 완전 해독에 집중했지만, 암호문을 꼭 전부 해독해야 할 필요는 없습니다. 일부만 해독되어도 암호문은 그 의미를 상실할 수 있기 때문입니다. 예를 들어 비밀 군사 지령의 위치와 시간, 규모만 해독되었다 하더라도 상대방은 상당한 정보를 얻을 수 있습니다. 하지만 암호문의 부분 정보의 중요성을 수학적으로 정의하긴 어렵습니다. 그럼 어떻게 수학적으로 모델링할 수 있을까요?
S. Goldwasser와 S. Micali는 1984년 ‘Probabilistic Encryption’4에서 중요한 정의를 몇 가지 내립니다. 기존의 결정적 공개 키 시스템을 탈피한 확률적 공개 키 시스템probabilistic public key cryptosystem, PPKC, 그리고 보안성의 중요한 지표가 되는 polynomial security와 semantic security입니다.
앞서 정의한 공개 키 시스템은 평문과 키가 동일하면 이에 대응되는 암호문이 항상 같습니다. 그러나 확률적 공개 키 시스템은 암호화 과정에 난수를 사용해 동일한 평문과 키에서도 여러 암호문이 나올 수 있습니다. 물론, 키를 알고 있는 사람은 쉽게 복호화할 수 있습니다. 이 난수는 엄밀하게는 함수들의 집합으로, 논문에서는 unapproximable trapdoor predicate이라 표현되고, 이차 잉여 판별 문제를 이용한 예시를 듭니다.
polynomial security는 indistinguishability라고도 불리며, 공격자가 두 평문 $m_1$과 $m_2$를 고르고 이 중 하나를 골라 암호화할 때 어느 것을 암호화했는지 다항 시간 안에 알 수 있는 $(m_1, m_2)$ 쌍을 다항 시간 내에 찾을 수 없는 성질입니다. 암호문의 구별이 불가능한 성질로, 비밀 키가 없으면 암호문을 복호화하기 어렵다는 뜻으로 이해할 수 있습니다.
semantic security는 공개 정보만으로 얻을 수 있는 정보의 양과 거기에 암호문까지 있을 때 다항 시간만큼 계산을 해도 얻을 수 있는 정보의 양이 같다는 뜻입니다. 달리 해석하자면 암호문에서 얻어낼 수 있는 평문 관련 정보가 단 0.1비트도 없다는 뜻입니다. “nothing is learned”라고 할 수 있고, one-time pad로 설명했던 perfect secrecy의 현실적인 해석입니다.
놀랍게도 PPKC는 polynomial security와 semantic security를 둘 다 가지며, 이 두 조건이 CPA 상에서 동치입니다.4 때문에 이 두 성질에 대한 공격 모델은 (indistinguishability 관점에서) 다음과 같이 기술됩니다. Alice는 확률적 튜링 기계(probabilistic Turing Machine)의 연산 능력을 가지고 있습니다.
- Bob은 공개 키와 비밀 키를 만들고, 공개 키와 기타 공개 정보 (키의 사이즈 $k$ 등)을 Alice에게 공개합니다.
- Alice는 다항 시간의 암호화와 기타 연산을 수행할 수 있습니다.
- Alice는 두 평문 $(m_0, m_1)$을 만들어 Bob에게 넘깁니다.
- Bob은 무작위로 $b \in {0, 1}$을 선택해 $m_b$를 공개 키로 암호화하여 Alice에게 넘깁니다.
- Alice는 다항 시간의 암호화와 기타 연산을 수행한 후 $b$를 추측하여 Bob에게 전달합니다.
Alice에겐 기본적으로 찍어서 $b$를 맞힐 확률 $\frac{1}{2}$이 있습니다. Alice가 다양한 연산을 수행하면 이 확률이 올라가면 올라가지 내려가진 않습니다. 그러나 다항 시간이 주어져도 Alice가 원래 평문을 알아낼 확률이 $\frac{1}{2} + \epsilon(k)$이고 $\epsilon(k)$가 negligible할 때 두 성질이 만족됩니다. 흔히 이를 IND-CPA, indistinguishable under chosen plaintext attack이라고 합니다.
앞서 보았던 RSA 같은 결정적 공개 키 암호화 시스템은 IND-CPA를 만족하지 않습니다. $(m_0, m_1)$에서 생성되는 암호문이 각각 유일하기 때문에 $(c_0, c_1)$을 계산해놓으면 항상 $b$를 고를 수 있기 때문입니다. 때문에 IND-CPA를 만족하려면 무작위 요소가 들어가되 복호화는 비밀 키를 통해 쉽게 될 수 있어야 합니다.
IND-CPA와 CPA 하에서의 semantic security는 동치라는 이 업적은 암호학이 꿈꾸는 secrecy를 현실적으로 semantic security로 옮겨놓았을 뿐만 아니라 모델링하기 쉬우면서 의미 있는 속성인 indistinguishability를 제안했다는 데 의의가 있습니다. 증명 가능한 보안의 첫 장을 열었기 때문입니다.
Chosen Ciphertext Attack
여기서 제시된 IND-(indistinguishability)는 chosen ciphertext attack 등에도 확장되어 널리 사용됩니다. IND-CCA는 공격자의 능력에 따라 보통 CCA1과 CCA2로 구분합니다.
- Bob은 공개 키와 비밀 키를 만들고, 공개 키와 기타 공개 정보 (키의 사이즈 $k$ 등)을 Alice에게 공개합니다.
- Alice는 다항 시간의 암호화와 기타 연산을 수행할 수 있고, 다항 시간만큼 복호화 오라클을 호출해 원하는 암호문을 복호화할 수 있습니다.
- Alice는 두 평문 $(m_0, m_1)$을 만들어 Bob에게 넘깁니다.
- Bob은 무작위로 $b \in {0, 1}$을 선택해 $m_b$를 공개 키로 암호화하여 ($C$) Alice에게 넘깁니다.
- Alice는 다항 시간의 암호화와 기타 연산을 수행할 수 있으며, 추가로
- non-adaptive한 경우 (IND-CCA1) 복호화 오라클은 호출할 수 없습니다.
- adaptive한 경우 (IND-CCA2) $C$를 제외한 모든 암호문을 복호화 오라클에 다항 시간만큼 넣어볼 수 있습니다.
- 최종적으로 Alice는 $b$를 추측하여 Bob에게 전달합니다.
CCA1과 CCA2에서도 semantic security와 indistinguishability는 동치입니다.5
Random Oracle Model
1993년에 제안된 Random Oracle Model은 간단히 말하자면, 해시 함수가 완벽한 난수 함수라고 가정하자는 모델입니다.6 기본적으로 해시 함수의 역상 저항성preimage resistance, 제 2 역상 저항성second preimage resistance, 충돌 저항성collision resistance는 난수 함수임을 보장하지 않습니다. 하지만 이상적이고 간편한 난수 생성기를 해시 함수로 설정하면 수많은 성질과 암호화 시스템이 안전함을 보일 수 있습니다. 대표적인 예시로 후에 설명할 RSA-OAEP가 있습니다.
아까 전에 indistinguishability를 다루며 확률적 공개 키 암호화 시스템이 두 성질을 만족한다고 했는데, 그럼 어떤 난수를 쓰는 걸까요? 난수를 직접 쓰기도 하지만, 조합을 하며 난수나 메시지를 해시하는 경우도 많습니다. 이 해시 함수가 난수라면 공격자가 해시 이전의 난수나 원본을 추적할 수도 없습니다.
Random Oracle Model은 정말 강력한 가정입니다. 실제로 난수 함수인 해시 함수는 발견되지 않았기 때문입니다. 하지만 당시 이 모델이 나왔을 때는 이에 기반한 암호 시스템이나 논문이 많이 연구되었다고 합니다. Random Oracle Model은 논문으로만 나와있던 ‘증명 가능한 보안’과 실생활에서 사용되는 구현체를 이어주는 다리 역할이 되었습니다.
다만 현재는 Random Oracle Model에서 벗어나려는 시도가 많습니다. 워낙 강력한 가정이기도 하고, Random Oracle Model에서는 안전하지만 그 어떤 구현체에서 해시 함수를 초기화해도 안전하지 않은 암호화 시스템이 존재하고 또 구축할 수 있기 때문입니다.7 더군다나 SHA-1 등의 해시 함수도 충돌 해시쌍을 만들 수 있기 때문에8 해시 함수에 대한 무조건적인 신뢰는 점차 줄어들 것으로 보입니다.
Random Oracle Model에 대한 묘사와 예시, 그리고 비판은 Matthew Green의 상세한 블로그를 참고해주시길 바랍니다.
Malleability
Malleability는 2003년에 제시된 암호화 시스템의 속성으로9, 어떤 평문 $m$을 암호화한 $c(pk, m)$을 알려진 함수 $f$에 대해 $c(pk, f(m))$으로 바꿀 수 있는 특성입니다 ($pk$는 공개 키 관련 정보입니다). 예를 들어 “김아무개에게 100,000원 입금”이 암호화된 메시지가 “김아무개에게 1,000,000원 입금”로 바뀌면 상당히 당황스러울 수밖에 없습니다. 위에서 살펴본 공격자는 암호문을 열람만 할 수 있는 수동적 공격자였으나 이와 같이 능동적으로 암호문을 변경해 전달할 수 있다면 의미 있는 성질이 됩니다. 그러므로 암호화 시스템은 변조가 어려운 non-malleability도 고려해야 합니다.
이 성질이 처음 나왔을 때는 ‘Indistinguishability와 다른 성질이 나왔다’라고 여겨져 많은 연구가 진행되었지만 이들 간의 동치 관계나 내포 관계 등이 밝혀졌습니다. 예를 들어, NM-CCA2는 IND-CCA2랑 동치입니다.
RSA-OAEP
OAEPOptimal Asymmetric Encryption Padding는 Random Oracle Model 하에서 안전한 trapdoor 함수와 사용되었을 때 IND-CPA를 보장하는 기법입니다.10 특히, RSA-OAEP는 IND-CCA2를 만족합니다.11
Indistinguishability를 생각하면 난수가 필요하고, malleability를 생각하면 조작할 수 없는 고정된 값이 필요합니다 (다만 OAEP는 malleability보다 먼저 제안되었습니다). OAEP는 이 두 가지 관점을 해시함수를 통해 결합해냅니다.
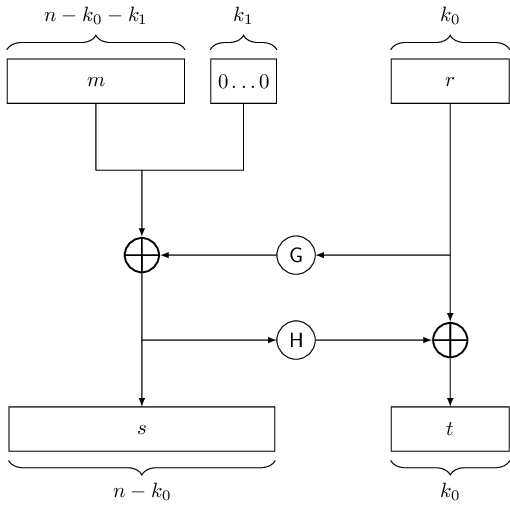
OAEP의 구조는 다음과 같습니다.
- $k_0$비트 난수 $r$, $k_1$비트의 $0$ 문자열, $n - k_0 - k_1$비트의 평문 $m$, $n-k_0$비트 해시 함수 $G$와 $k_0$비트 해시 함수 $H$를 준비합니다.
- $m\ \vert\vert\ 0^{k_1}$에 $G(r)$을 xor하여 $s = (m\ \vert\vert\ 0^{k_1}) \oplus G(r)$를 만듭니다.
- $r$에 $H(s)$를 xor하여 $t$를 만듭니다.
- 그 결과로 $s \ \vert \vert \ t$을 얻었습니다.
이렇게 인코딩된 문자열을 RSA로 암호화하면 확률적 공개 키 암호화가 됩니다. 복호화도 쉽게 할 수 있습니다.
- $t$에 $H(s)$를 xor하여 $r$을 얻습니다.
- $s$에 $G(r)$을 xor하여 $m\ \vert\vert\ 0^{k_1}$를 얻습니다.
마무리
요즘은 타원곡선 암호Elliptic Curve Cryptography, ECC와 양자내성암호Post-Quanum Cryptography, PQC, 격자 기반 암호Lattice-Based Cryptography, LBC 등 다양한 암호가 활발하게 연구되고 있습니다. 컴퓨터의 연산속도는 30년 전과는 비교도 할 수 없을 만큼 빨라졌습니다. 공격 기법 또한 더 다채로워지고 알고리즘 구조나 구현 실수로 인해 보안 사고가 일어나기도 했습니다. 그럼에도 매 순간 암호화는 전 세계에서 사용되고 있습니다. 특정 제약조건 하에서는 안전함이 엄밀하게 증명되었기 때문입니다. 오늘도 창과 방패의 대결은 계속되고 있습니다.
각주
-
Diffie, W., & Hellman, M. (1976). New directions in cryptography. IEEE transactions on Information Theory, 22(6), 644-654. ↩
-
이산 대수 문제는 NP-complete은 아니지만 일반적으로 다항 시간 안에 풀 수 없으리라 여겨집니다. ↩
-
Rivest, R. L., Shamir, A., & Adleman, L. (1978). A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2), 120-126. ↩
-
Goldwasser, S., & Micali, S. (1984). Probabilistic encryption. Journal of computer and system sciences, 28(2), 270-299. ↩ ↩2
-
Watanabe, Y., Shikata, J., & Imai, H. (2003, January). Equivalence between semantic security and indistinguishability against chosen ciphertext attacks. In International Workshop on Public Key Cryptography (pp. 71-84). Springer, Berlin, Heidelberg. ↩
-
Bellare, M., & Rogaway, P. (1993, December). Random oracles are practical: A paradigm for designing efficient protocols. In Proceedings of the 1st ACM conference on Computer and communications security (pp. 62-73). ↩
-
Canetti, R., Goldreich, O., & Halevi, S. (2004). The random oracle methodology, revisited. Journal of the ACM (JACM), 51(4), 557-594. ↩
-
SHAttered. (2017). Retrieved 21 November 2020, from https://shattered.io/ ↩
-
Dolev, D., Dwork, C., & Naor, M. (2003). Nonmalleable cryptography. SIAM review, 45(4), 727-784. ↩
-
Bellare, M., & Rogaway, P. (1994, May). Optimal asymmetric encryption. In Workshop on the Theory and Application of of Cryptographic Techniques (pp. 92-111). Springer, Berlin, Heidelberg. ↩
-
Fujisaki, E., Okamoto, T., Pointcheval, D., & Stern, J. (2001, August). RSA-OAEP is secure under the RSA assumption. In Annual International Cryptology Conference (pp. 260-274). Springer, Berlin, Heidelberg. ↩