Post-Quantum Cryptography

1. Introduction

양자 컴퓨터가 언제 상용화가 가능할지는 예측이 힘들지만 양자 컴퓨터의 개발 이후 영향을 받을 분야는 굉장히 많고 그런 분야들에서는 관련 연구를 활발하게 진행하고 있습니다.

한편 양자 컴퓨터의 이론적 개념은 양자 역학과 컴퓨터 과학에서의 계산 이론 분야의 깊은 이해를 요구하기 때문에 (저를 포함한) 많은 사람들은 양자 컴퓨터의 개념을 매우 피상적으로 알고 있거나 기능을 잘못 이해해서 양자 컴퓨터가 상용화되면 모든 암호 체계가 붕괴된다고 착각하는 경우가 종종 있습니다.

이번 글에서는 양자 컴퓨터 시대를 대비하는 Post-Quantum Cryptography에 대해 알아보겠습니다. 양자 컴퓨터에 대한 깊은 이론적 지식은 최대한 배제했습니다. 양자 컴퓨터에 대한 포스팅은 evenharder님이 작성중이시고 여기에서 확인할 수 있습니다.

2. Basic Information

고전 컴퓨터는 0 혹은 1을 담는 비트 단위로 이루어져 있습니다. 반면 양자 컴퓨터는 큐빗 단위로 이루어져 있고 큐빗에는 0 혹은 1이 들어있는 대신 0과 1이 마치 슈뢰딩거의 고양이와 같이 중첩되어 있습니다. 0과 1이 중첩되어 있기 때문에 큐빗을 관측했을 때 0으로 관측될 확률은 $p$, 1으로 관측될 확률은 $1-p$입니다.

세간에 알려진 바와 다르게 양자 컴퓨터가 모든 문제를 고전 컴퓨터보다 월등하게 빠른 속도로 풀어내지는 않습니다. 다만 일부 문제에서는 월등하게 빠르게 해결할 수 있고, 특히 Shor’s algorithm과 Grover’s algorithm은 여러 암호 시스템에 영향을 줍니다.

A. Shor’s algorithm

Shor’s algorithm은 인수분해 혹은 이산 대수 문제를 빠르게 풀어주는 알고리즘입니다. 알고리즘 자체에 대해서 이해하려면 quantum fourier transform(양자 푸리에 변환)이라는 무시무시한게 필요하므로 알고리즘에 대한 설명은 생략하겠습니다.

Shor’s algorithm을 이용하면 RSA와 ECC 모두 $log N$에 대한 다항 시간에 해결 가능합니다. 그렇기 때문에 RSA와 ECC가 모두 안전하지 못하게 됩니다.

B. Grover’s algorithm

Grover’s algorithm은 정렬되어있지 않은 리스트에서 특정 데이터를 $O(\sqrt{N})$에 찾는 알고리즘입니다. 고전 컴퓨터에 익숙한 사람이면 굉장히 의아하겠지만 $O(N)$이 아니라 $O(\sqrt{N})$이 맞습니다.

이 알고리즘을 이용하면 AES와 같은 대칭키 암호에서 키의 전수 조사를 $O(\sqrt{N})$에, 해쉬 충돌쌍을 $O(\sqrt[3]{N})$에 수행할 수 있습니다.

A, B에서 확인한 것과 같이 양자 컴퓨터로 인해 가장 큰 문제가 발생하는 암호 시스템은 공개키 암호 시스템입니다. 대칭키 암호 시스템에서는 단순히 키 길이를 2배 늘리기만 하면 고전 컴퓨터와 동일한 안전성을 가지기 때문에 다른 취약점이 발견되지 않는한 AES-192 혹은 AES-256 정도면 양자 컴퓨터가 상용화된 이후에도 충분히 안전하다고 말할 수 있습니다.

3. Post-Quantum Cryptography 표준화

AES가 전 세계읙 공모를 거쳐 만들어진 것과 같이 Post-Quantum Cryptography 또한 NIST에서 주관하는 공모를 통해 선정 과정이 진행중입니다.(링크)

공모를 통해 69개의 후보가 제안되었고 안전성, 성능, 기타 성질들을 고려해 라운드 1, 라운드 2를 거쳐 후보를 줄여나가며 2020년 11월 기준으로 라운드 3에 도달했습니다. 라운드 3에는 7개의 후보가 Finalist로, 8개의 후보가 Alternate candidates로 남아있습니다.

라운드 3까지 살아남은 후보들은 크게 Lattice-based, Code-based, Multivariate로 구분할 수 있습니다. 특히 7개의 Finalist 후보 중에서 5개가 Lattice-based이고 Code-based, Multivariate는 각각 1개입니다. Code-based, Multivariate는 아주 간략하게만 설명드리고 표준으로 선정될 것이 유력해보이는 Lattice-based에 대해서는 길게 설명드리겠습니다.

A. Code-based

여기서 말하는 code는 우리가 흔히 생각하는 프로그래밍 언어의 code가 아니라 부호 이론(Coding Theory)에서 배우는 code입니다.

얕은 이해만을 목표로 둔다면 부호 이론 전체를 익힐 필요는 없지만 꼭 Hamming Code라는 개념은 이해할 필요가 있습니다. 정말 간략하게 설명을 해보자면 Hamming Code는 메시지의 송, 수신 과정에서 error correction이 가능한 오류 정정 부호의 일종입니다. 이 글을 참고해보세요.

이제 Code-based cryptosystem 중에 유일하게 Round 3에 올라간 McEliece 구조를 설명드리겠습니다.

이 구조에서 나오는 matrix는 전부 binary matrix(0 혹은 1으로만 이루어진 matrix)입니다. 우선

Hamming Code의 개념이 적용되어 Hamming distance가 $w$ 이하인 오류는 스스로 복구 가능한 matrix $G$
nonsingular matrix $S$
각 행과 열에 1이 정확히 1개씩 있는 permutation matrix $P$ 이 3개가 secret key이고 $X = SGP$가 public key입니다.

암호화 과정은 $c = mX + e$입니다. 이 때 $e$는 Hamming distnace가 $w$입니다.

복호화 과정은 $cP^{-1}$을 계산해보면 $cP^{-1} = (mX + e)P^{-1} = (mS)G + eP^{-1} = m’G + e’$이고 $G$의 조건으로 인해 $e’$은 무시되어 $m’$을 구할 수 있게 됩니다. 마지막으로 $m’S^{-1}$을 계산하면 $m$을 복원할 수 있습니다.

이 cryptosystem은 1978년에 제안된 것임에도 불구하고 메이저한 공격이 나오지 않았습니다.

B. Multivariate

Multivariate cryptosystem은 변수가 여러개(Multivariate)인 연립방정식을 푸는 문제가 NP-complete임을 이용한 방식입니다.

이 cryptosystem에서는 inverse가 존재하는 matrix $L_1, L_2$를 비밀키로 설정하고 미리 해를 구하기 쉽도록 특수한 형태로 만들어둔 matrix $F$에 대해 공개키는 $L_1 \circ F \circ L_2$로 둡니다.

그러면 공개키만 아는 사람은 $L_1 \circ F \circ L_2$으로 만들어지는 Multivariate 연립방정식을 풀어낼 수 없지만 비밀키 $L_1, L_2$를 아는 사람은 $L_1^{-1}, L_2^{-1}$을 양쪽에 곱해서 $F$를 알아낸 후 Multivariate 연립방정식을 풀어낼 수 있습니다.

다만 Round 3에서 Rainbow가 유일하게 Multivarate cryptosystem인데 2020년 10월에 공개된 논문에 따르면 최대 $2^{55}$의 시간 복잡도에 공격이 가능합니다.(논문 링크) 최근에 나온 논문이라 아직 읽지는 못했지만 이 논문이 사실이라면 Rainbow는 탈락할 것으로 예상됩니다.

C. Lattice-based

Lattice-based cryptography를 이해하기 위해서는 먼저 Lattice라는 개념에 대해 알아야 합니다.

선형대수를 배우신 분이라면 basis라는 개념을 알 것입니다. 이 basis 각각에 정수를 곱한 후에 합해서 얻어지는 vector들이 Lattice입니다.

예를 들어 2차원 공간에서 basis가 $\begin{bmatrix}-1 \ 2 \end{bmatrix}, \begin{bmatrix}1 \ 2 \end{bmatrix}$ 일경우 Lattice를 2차원 공간의 점으로 표현하면 아래와 같습니다.

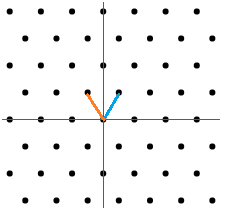
그림에서 확인할 수 있듯 $\begin{bmatrix}-1 \ 2 \end{bmatrix}, \begin{bmatrix}0 \ 4 \end{bmatrix}, \begin{bmatrix}-2 \ 0 \end{bmatrix}$ 등은 Lattice에 포함되지만 $\begin{bmatrix}0 \ 3 \end{bmatrix}, \begin{bmatrix}1 \ 0 \end{bmatrix}$ 등은 그렇지 않습니다.

RSA에서는 소인수분해의 어려움을, ECC에서는 타원 곡선 위에서 이산 대수 문제의 어려움을 이용해서 공개키 암호 시스템을 만들었습니다.

Lattice에서도 어려운 문제들이 여럿 있습니다. 첫 번째로 Shortist vector problem(SVP)는 Lattice 안의 vector 중에서 norm이 가장 작은 vector를 찾는 문제를 말합니다. 두 번째로 Closest vector problem(CVP)는 주어진 vector $u$에 대해 Lattice 안의 vector $v$ 중에서 $u - v$가 가장 작은 vector $v$를 찾는 문제를 말합니다. 이 두 문제는 Lattice가 $n$차원일 때 $n$의 exponential에 비례한 시간의 해결법이 존재하고 고전 컴퓨터와 양자 컴퓨터 모두에서 그보다 더 효율적인 방법은 제시되지 않았습니다.

실제 공개키 암호에서 주로 사용되는 문제는 이 둘을 응용한 Learning With Errors(LWE)입니다. Learning With Errors를 통해 만든 간단한 형태의 공개키 암호 시스템을 아래에 소개하겠습니다.

키성생 절차

소수 $q$를 정합니다.
vector $a_i(1 \leq i \leq m)$을 $\mathbb{Z}^n_q$에서 랜덤하게 정합니다.
vector $s$ 또한 $\mathbb{Z}^n_q$에서 랜덤하게 정합니다.
vector $b_i(1 \leq i \leq m) = a_i \cdot s^{T} + e_i$로 둡니다. $e_i$는 아주 작은 오차를 의미합니다.
공개키는 $a, b, q$이고 비밀키는 $s$입니다.

암호화 절차

1 bit 크기의 메시지 $m$을 암호화하기 위해 $S \in Z_n$을 랜덤하게 정합니다. 즉 $S$를 통해 $a_i$에서 일부 vector를 사용할 것입니다.
암호화의 결과는 $(u = \Sigma_{i \in S}{a_i}, v = m/2 + \Sigma_{i \in S}{b_i})$입니다.
복호화를 하는 사람은 $v - u \cdot s^{T}$가 0에 가까운지 $1/2$에 가까운지 확인합니다.($e_i$로 인해 같을 수는 없습니다.) 0에 가깝다면 메시지는 0이고 1/2에 가깝다면 메시지는 1입니다.

갑자기 vector를 이용한 연산이 쏟아져나와 굉장히 혼란스러울텐데 이해에 조금이라도 도움이 되고자 $n = 1$, 즉 그냥 $a_i$와 $b_i$가 정수일 때의 상황을 예로 들어 과정을 풀어서 설명해보겠습니다.

먼저 $q = 97, a = [69, 22, 82, 66, 73], b = [58, 16, 25, 41, 77], e = [4, 3, 3, 2], s = 5$로 두겠습니다. 위의 식에서 설명한 것과 같이 $b_i = a_i \cdot s + e_i$가 잘 성립합니다.

이후 메시지 0을 암호화하기 위해 $S = [1, 3, 5]$으로 선택했습니다. 즉 5가지 원소 중에서 1, 3, 5번째 원소를 이용할 것입니다.

1, 3, 5번째 원소의 합을 구하면 $u = a_1 + a_3 + a_5 = 69 + 82 + 73 \equiv 30(mod \ q), v = b_1 + b_3 + b_5 = 58 + 25 + 77 \equiv 63(mod \ q)$입니다.

복호화를 하는 사람은 $v - u \cdot s = 63 - 30 \cdot 5 \equiv 10(mod \ q)$을 계산합니다. 10은 $2^{-1} \equiv 48(mod \ q)$보다 0에 더 가까우므로 메시지가 0임을 알 수 있습니다.

지금 예시는 1차원이였고 $n$차원에서는 $a_i, b_i, u_i, v_i$가 vector가 된다는 차이가 있을 뿐 상황은 동일합니다.

만약 $e_i$가 없었다면 $b_i = a_i \cdot s$이라는 식으로부터 비밀키 $s$를 복원하는 것이 굉장히 쉬웠을텐데 $e_i$가 각 식에 섞여들어가서 $a_i, b_i$만 보고는 $s$를 알아내는게 어렵게 되었습니다.

지금 글에서 소개한 내용은 1비트의 메시지만 보낼 수 있는 아주 기초적인 형태의 lattice-based cryptosystem입니다. 실제 표준화 단계에서 제안된 NTRU, SABER 등의 암호가 어떤 구조로 되어있는지는 다음 포스팅에서 다루게 될 것으로 보입니다.

4. Conclusion

이번 글을 통해 Post Quantum Cryptography에 대한 얕은 지식을 습득할 수 있었을 것입니다.

Shor’s algorithm으로 인해 사실상 기존의 공개키 암호 시스템이 거의 다 박살나게 되었지만 아직 상용화까지는 까마득하게 먼 것으로 추정되고 각 기관들은 일찍이부터 대비를 해오고 있습니다.

복잡한 수학이 쓰이지 않아 이해가 어렵지 않았던 RSA, ECC 등에 비해 Post Quantum Cryptography는 공부를 하는 입장에서 까다로운 면이 없지 않지만 그럼에도 불구하고 공부를 해볼 가치가 있는 내용이라고 생각합니다.