jh05013's profile image

jh05013

January 19, 2021 00:00

이 글은 튜링 기계와 NP-complete에 대한 기본 배경지식을 전제로 합니다.

서론

이분 그래프가 주어졌을 때 최대 매칭을 구하는 문제는 알고리즘 문제 풀이에서 잘 알려져 있습니다. 심지어 일반적인 그래프가 주어져도 최대 매칭을 다항 시간에 구할 수 있습니다. 그러므로 완전 매칭이 존재하는지도 같은 방법으로 구할 수 있습니다. 하지만 완전 매칭의 개수를 구하라고 하면 어떻게 될까요?

카운팅 문제와 #P-완전

NP-완전성을 이야기할 때는 문제가 결정 문제로 한정됩니다. 예를 들어 최대 클릭 문제는 “가장 큰 클릭은 무엇인가?”가 아니라 “크기가 $k$ 이상인 클릭이 존재하는가?”입니다. 그렇다면 경우의 수를 구하는 문제에 대해 NP-완전성을 정의할 수 있을까요?

이를 위해, 경우의 수 문제에 대한 튜링 기계를 새로 정의합시다. Leslie Gabriel Valiant는 다음과 같이 카운팅 튜링 기계 (counting Turing machine)를 정의했습니다.¹ 비결정론적 튜링 기계와 같은데, “경우의 수를 출력하는 테이프”가 추가로 들어있습니다. 이 기계는 입력이 주어지면 그 입력이 accept되도록 계산을 진행하는 경우의 수를 출력합니다.

카운팅 튜링 기계로 다항 시간에 풀 수 있는 문제의 집합을 #P라고 합니다. 예를 들어, 이분 그래프의 완전 매칭의 개수를 구하는 문제는 #P입니다. 정점 집합 $A$와 $B$로 분리된 이분 그래프가 주어졌을 때, $B$의 정점의 순서를 $O(\mid B \mid !)$개의 경우 중 하나로 섞습니다. 그 후 모든 $i$에 대해 $A$와 $B$의 $i$번째 정점 사이에 간선이 존재하고, 그렇게 매칭을 해서 남는 정점이 없으면 accept합니다. 그러면 accept하는 경우의 수는 정확히 이 그래프의 완전 매칭의 개수와 같고, 이 과정은 다항 시간에 계산할 수 있습니다.

그 다음에는 NP-완전에서 했던 것처럼 환원을 정의합니다. 문제 $P$와 $Q$가 있을 때, 다음을 만족하는 함수 쌍 $(f, g)$를 $P$에서 $Q$로의 다항 시간 환원이라고 부릅니다.

• $f$는 $P$의 입력에서 $Q$의 입력으로 가는 함수이고, 다항 시간에 계산할 수 있습니다.
• $g$는 $Q$의 출력에서 $P$의 출력으로 가는 함수이고, 다항 시간에 계산할 수 있습니다.
• $P$의 입력 $x$에 대해, 올바른 출력을 $P(x)$라고 합시다. 그러면 $P(x) = g(Q(f(x)))$입니다. 즉 $Q$를 풀 수 있으면 그 문제를 한 번만 써서 $P$를 풀 수 있습니다.

나머지는 NP-완전에서 했던 것과 똑같습니다. 모든 #P 문제를 문제 $A$로 다항 시간에 환원할 수 있으면 $A$를 #P-hard라고 합니다. 그와 동시에 $A$ 자신이 #P이면 #P-완전 (#P-complete)이라고 합니다.

준비 작업

이분 그래프의 완전 매칭의 개수를 구하는 문제가 #P-완전임을 증명해봅시다.

• 위에서 보았듯이 이 문제는 #P입니다.
• 카운팅 SAT, 즉 변수에 참, 거짓을 대입하여 주어진 CNF를 참으로 만드는 경우의 수를 구하는 문제는 #P-hard입니다. Cook-Levin 정리와 같은 방법으로 증명할 수 있습니다.
• 카운팅 3-SAT도 #P-hard입니다. 카운팅 SAT에서 다항 시간 환원을 하면 됩니다. 그 방법도 SAT을 3-SAT으로 환원하는 것과 비슷한데, 새로 만들어지는 변수의 값이 유일하도록 clause를 더 추가합니다. 예를 들어 $(x_1 \vee x_2 \vee x_3 \vee x_4)$는 $(x_1 \vee x_2 \vee y_1) \wedge (\neg y_1 \vee x_3 \vee x_4) \wedge (\neg x_3 \vee y_1 \vee y_1) \wedge (\neg x_4 \vee y_1 \vee y_1)$로 바뀝니다.¹
• 이제 0과 1로 이루어진 행렬의 permanent를 구하는 문제가 #P-완전임을 증명합니다. 카운팅 3-SAT에서 다항 시간 환원을 하면 되는데, 자세한 내용은 후술합니다. 크기가 $n$인 행렬의 permanent의 정의는 다음과 같습니다. Determinant의 정의에서 $(-1)^{\cdots}$가 사라진 것으로 생각하면 됩니다.

$Perm(X) = \sum_{\sigma} \prod_{i=1}^{n} X_{i,\sigma(i)}$

• 정점 집합 $A = {a_1, \cdots, a_n}$과 $B = {b_1, \cdots, b_m}$로 분리된 이분 그래프가 주어졌을 때, $n \neq m$이라면 완전 매칭의 개수는 당연히 영행렬의 permanent와 같습니다. $n = m$이라면, $a_i$와 $b_j$를 잇는 간선이 있으면 $X_{i,j}$를 1로 두고, 없으면 0으로 둡시다. 그러면 완전 매칭의 개수는 $Perm(X)$입니다. 0-1 permanent가 #P-hard이므로, 이분 그래프의 완전 매칭의 개수도 #P-hard입니다. 따라서 이 문제는 #P-완전입니다.

가장 어려운 부분은 카운팅 3-SAT을 0-1 permanent로 환원하는 것입니다.

Permanent는 #P-hard이다

0-1 permanent 말고, 원소의 값으로 -1, 0, 1, 2, 3이 들어갈 수 있는 행렬이 #P-hard라는 것부터 증명합시다. (이 행렬의 permanent가 음수일 수도 있으므로 이 문제는 #P가 아닙니다.)

구체적으로, 3-CNF $F$가 주어졌을 때, 절의 개수를 $c(F)$, 변수의 값을 결정해서 식을 참으로 만드는 경우의 수를 $s(F)$라고 합시다. 이때 모든 $F$에 대해 $Perm(f(F)) = 4^{5c(F)}s(F)$가 성립하는 함수 $f$를 찾습니다. 그러면 $Perm(f(F))$가 주어졌을 때 $s(F)$를 다항 시간에 구할 수 있으므로, 이 함수를 그대로 써서 다항 시간 환원을 할 수 있습니다.

우리가 볼 환원은 Valiant의 논문에서 제시되었습니다.² Amir Ben-Dor., Shai Haleviy의 논문에서 다른 환원을 볼 수 있습니다. 전체적인 흐름은 비슷하나 구체적인 방법이 다르며, $Perm(f(F)) = 12^{c(F)}s(F)$입니다.³

사이클 덮개

기본 아이디어는 행렬을 인접 행렬로 생각하는 것입니다. 즉 행렬 $X$가 주어졌을 때, 인접 행렬이 $X$인 그래프를 생각합시다. 행렬에 적힌 수는 간선의 가중치가 되며, 적힌 수가 0이면 간선이 없습니다.

그러면 $Perm(X)$는 어떻게 될까요? 순열을 그래프로 옮기면, 각 정점을 정확히 한 번씩 사용하는 사이클의 집합이 됩니다. 이를 사이클 덮개 (cycle cover)라고 부릅시다. 순열 $\sigma$로 사이클 덮개를 만들면 $\prod_{i=1}^{n} X_{i,\sigma(i)}$는 사이클 덮개에 사용된 모든 간선의 가중치의 곱이 됩니다. 따라서 $Perm(X)$는 가능한 모든 사이클 덮개에 대해 “간선의 가중치의 곱”의 합과 같습니다.

이제 3-CNF $F$가 주어지면 그래프 $f(F)$를 잘 만들어서, $F$가 참이 되는 변수 값은 permanent에 정확히 $4^{5c(F)}$만큼 기여하고, 거짓이 되는 변수 값은 0만큼 기여해야 합니다.

변수

이 그래프는 여러 개의 구성 요소를 짜맞추는 식으로 만들어집니다. 이 글에서는 “부품”이라고 부릅시다.

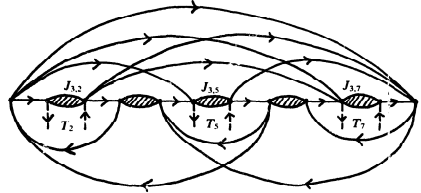
첫 번째는 변수입니다. 변수 $x_i$를 나타내는 부품 $T_i$는 다음과 같습니다. 모든 간선의 가중치는 1입니다.

위와 아래 정점은 이 그림에 제시된 것을 제외하면 다른 어느 정점과도 연결되지 않습니다. 따라서 사이클 덮개는 반드시 위에서 아래로 가는 가운데 간선을 사용해야 하고, 왼쪽과 오른쪽 간선 중 정확히 하나를 사용해야 합니다. 왼쪽은 $x_i$ 변수를 참으로, 오른쪽은 거짓으로 설정했음을 나타냅니다.

절에 들어있는 변수

$i$번째 절에 변수 $x_k$ 또는 $\neg x_k$가 들어있을 때, 이를 정점 4개짜리 부품 $J_{i k}$로 나타냅니다. 이 간선들의 가중치는 다음 인접 행렬로 표현됩니다.

$$J = \begin{matrix} 0 & 1 & -1 & -1
1 & -1 & 1 & 1
0 & 1 & 1 & 2
0 & 1 & 3 & 0 \end{matrix}$

2번과 3번 정점은 1, 4를 제외하면 다른 어느 정점과도 연결되지 않습니다. 그러므로 사이클 덮개가 $J_{i k}$ 부품 바깥에서 안으로 들어오려면 정점 1이나 4를 통해 들어와야 하고, 부품을 나가는 것도 1이나 4를 통해서만 가능합니다.

이 행렬은 다음과 같은 특징을 갖고 있습니다.

• $Perm(J) = 0$입니다. 따라서, 사이클 덮개가 부품 $J_{i k}$의 바깥에서 안으로 들어오는 게 아니라 $J_{i k}$ 안에서만 사이클을 만들면, 그런 사이클 덮개들의 가중치 곱이 서로 상쇄되어 그 합은 0이 됩니다. 결론적으로 그런 사이클 덮개는 permanent에 아무것도 기여하지 않습니다.
• $J$에서 $\gamma$번째 행과 $\delta$번째 열을 지워서 만든 행렬을 $J(\gamma, \delta)$라고 하면, $J(1;1), J(4;4), J(1;1)(4;4)$의 permanent는 모두 0입니다. 따라서, 사이클 덮개가 정점 1이나 4를 바깥에서 방문하기는 하는데 안으로 들어오지 않고 바로 밖으로 나가면, 그런 사이클 덮개들의 가중치 곱이 서로 상쇄되어 그 합은 0이 됩니다.
• 그러므로, 사이클 덮개의 가중치 곱이 상쇄되지 않으려면 모든 부품을 정확히 한 번씩 통과해야 합니다. 여기서부터는 모든 사이클 덮개가 모든 $J_{i k}$를 한 번씩 통과한다고 가정하겠습니다.
• $J(1;4), J(4;1)$의 permanent는 모두 4입니다. 따라서, 사이클 덮개의 가중치 곱은, 이 부품의 개수를 $k$라고 할 때 $4^k$가 됩니다.

이제 각각의 $J_{i k}$를 변수 부품 $T_k$에 끼워넣습니다. 즉 변수가 $x_k$이면 $T_k$의 왼쪽 화살표에, $\neg x_k$이면 오른쪽 화살표에 끼워넣습니다. 그러면 $T_k$의 가운데 화살표를 사용하는 사이클은 왼쪽이나 오른쪽 화살표를 타면서, 그 사이에 있는 $J_{i k}$를 모두 통과하게 됩니다.

절

각각의 절 $C_i$는 다음 부품 $R_i$로 나타냅니다. 모든 간선의 가중치는 1입니다.

1, 3, 5번째 타원은 변수 부품 $J_{i k}$ 세 개를 나타냅니다. 앞으로 이 변수 부품을 “타원”으로 부릅시다. 2, 4번째 타원은 변수와 관련이 없지만, 구조는 $J_{i k}$와 똑같습니다. 각 $R_i$에 타원이 5개 있으므로, 전체 타원의 개수는 $5c(F)$입니다.

이 부품은 다음과 같은 특징을 갖고 있습니다.

• 이 절에서 참인 변수의 타원은 부품 $T_k$에 있는 사이클이 이미 통과했기 때문에, 다시 통과할 수 없습니다. 나머지 부품은 모두 통과해야 합니다.
• 이 절의 모든 변수가 거짓이라면, $R_i$ 내부에서 모든 타원을 통과하는 사이클 덮개를 만들어야 하는데, 그런 덮개는 존재하지 않습니다.
• 이 절의 적어도 한 변수가 참이라면, $R_i$ 내부에서 참인 변수를 제외한 나머지 타원을 통과하는 사이클 덮개를 만들어야 하는데, 그런 덮개는 (타원 내부에서의 경로를 고려하지 않으면) 정확히 하나 존재합니다.

따라서, $F$를 참으로 만드는 변수 값은 사이클 덮개에 (타원 내부에서의 경로를 고려하지 않으면) 정확히 일대일 대응되고, 이 변수 값은 permanent에 정확히 $4^{5c(F)}$만큼 기여합니다. 반대로 $F$를 거짓으로 만드는 변수 값은 permanent에 아무것도 기여하지 않습니다. 따라서 $Perm(f(F)) = 4^{5c(F)}s(F)$입니다.

0-1 Permanent는 #P-hard이다

각 원소가 -1, 0, 1, 2, 3 중 하나인 행렬의 permanent가 #P-hard임을 증명했습니다. 하지만 우리가 증명해야 되는 것은 각 원소가 0, 1 중 하나인 행렬의 permanent가 #P-hard라는 것입니다. 그래서 다음 과정을 거쳐서 “-1, 0, 1, 2, 3 permanent” 문제를 “0-1 permanent” 문제로 환원합니다.

1. 적당한 $\alpha$를 잡아서, “-1, 0, 1, 2, 3 permanent” 문제를 “0, 1, …, $\alpha$ permanent” 문제로 환원합니다.
2. 적당한 $\beta$를 잡아서, “0, 1, …, $\alpha$ permanent” 문제를 “0, $2^0$, $2^1$, …, $2^\beta$ permanent” 문제로 환원합니다.
3. “0, $2^0$, $2^1$, …, $2^\beta$ permanent” 문제를 “0-1 permanent” 문제로 환원합니다.

이 과정은 Amir Ben-Dor., Shai Haleviy의 논문에서 제시한 것입니다.³ Valiant의 증명은 many-one reduction이 아닌 Turing reduction을 사용합니다. 즉 0-1 permanent 문제를 한 번이 아니라 여러 번 풀어야 하고, 이는 many-one reduction보다 약한 증명입니다.²

-1, 0, 1, 2, 3에서 음이 아닌 정수로

이 행렬의 모든 원소의 절댓값이 3 이하이므로, $\mid Perm(X) \mid \leq n!3^n$입니다. 한편, $-M \leq x \leq M$을 알고 있을 때 $x \text{mod} (2M+1)$이 주어지면 $x$의 값은 유일하게 결정됩니다.

$Q = 2n!3^n+1$이라고 합시다. $X$의 각 원소를 mod $Q$ 하여 새로운 행렬 $X’$을 만들고, $P = Perm(X’) \text{mod} Q$라고 합시다. 이제 $P < \frac{Q}{2}$이면 $Perm(X) = P$이고, 아니면 $Perm(X) = P-Q$입니다. 따라서 mod $2n!3^n+1$를 하면 첫 번째 환원이 됩니다.

음이 아닌 정수에서 0과 2의 거듭제곱으로

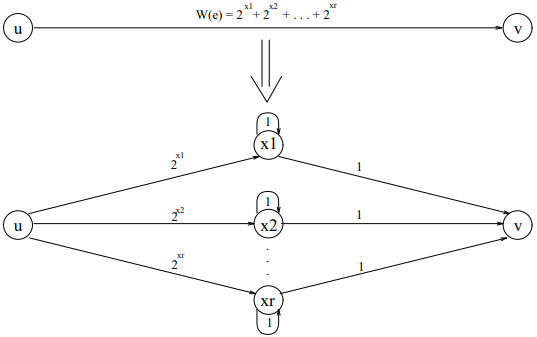
이제 행렬 $X$의 모든 원소는 0 이상의 정수입니다. 다시 행렬을 그래프로 바꿔서 생각합니다. 간선 $uv$의 가중치가 $w > 0$일 때, 이 간선을 다음 과정을 따라 교체합니다.

• $0 \leq x_1 < \cdots < x_r, w = 2^{x_1} + \cdots + 2^{x_r} $이라고 합시다. 이진 전개에 따라 이러한 $x_1, \cdots, x_r$은 항상 존재하고, $r = O(log w)$입니다.
• 각 $x_i$마다 새로운 정점 $x_i$를 만들고, 가중치 1의 self-loop를 긋습니다.
• $u$에서 각 $x_i$로 가중치 $2^{x_i}$의 간선을 긋습니다.
• 각 $x_i$에서 $v$로 가중치 1의 간선을 긋습니다.

만약 사이클 덮개가 간선 $uv$를 사용하지 않는다면, 이는 $r$개의 self-loop 전부를 사용한 사이클 덮개로 바꿀 수 있습니다. 이때 모든 사이클 덮개에 대한 permanent의 합은 $1$입니다. 사용한다면, 이는 가중치 $2^i$의 간선 중 하나와, $x_i$를 제외한 $r-1$개의 self-loop를 사용한 사이클 덮개로 바꿀 수 있습니다. 이때 permanent의 합은 $w$입니다. 양쪽 모두 간선 $uv$가 permanent에 기여하는 정도가 바뀌지 않기 때문에, permanent의 값도 바뀌지 않습니다.

모든 간선을 이렇게 교체하면 두 번째 환원이 완료됩니다.

0과 2의 거듭제곱에서 0, 1로

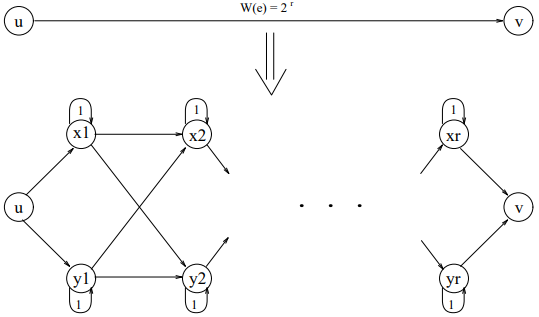
이제 그래프 $X$의 모든 간선의 가중치는 2의 거듭제곱입니다. 간선 $uv$의 가중치가 $2^r$일 때, 이 간선을 다음 과정에 따라 교체합니다.

• 각 $1 \leq i \leq r$마다 새로운 정점 $x_i$와 $y_i$를 만들고, 가중치 1의 self-loop를 긋습니다.
• $u$에서 $x_1$과 $y_1$으로 가중치 1의 간선을 긋습니다.
• 각 $1 \leq i < r$마다, $x_i$와 $y_i$에서 $x_{i+1}$과 $y_{i+1}$로 (총 $2^2$개의 경우를 모두 사용합니다) 가중치 1의 간선을 긋습니다.
• $x_r$과 $y_r$에서 $v$로 가중치 1의 간선을 긋습니다.

두 번째 환원과 같은 이유로, permanent의 값은 바뀌지 않습니다. 모든 간선을 이렇게 교체하면 세 번째 환원이 완료되어, 드디어 0-1 permanent가 #P-hard임이 증명됩니다.

결론

지금까지 경우의 수 문제에서 NP-완전의 개념을 어떻게 정의하는지, 그리고 이분 그래프의 완전 매칭을 세기가 왜 어려운지를 살펴보았습니다.

존재성을 결정하는 것은 쉽지만 경우의 수를 결정하는 것은 어려운 사례는 이외에도 여러 개 찾을 수 있습니다.

• 2-SAT은 선형 시간에 풀 수 있지만, 카운팅 2-SAT은 #P-완전입니다.¹
• 이분 그래프의 완전 매칭이 아니라 그냥 매칭의 개수를 세는 문제도 #P-완전입니다.¹
• 그래프에서 두 점 사이의 단순 경로의 개수를 세는 문제는 #P-완전입니다.¹
• 위상 정렬의 개수를 세는 것은 #P-완전입니다.⁴
• CNF와 비슷한데 $\vee$와 $\wedge$를 뒤바꾼 것을 DNF (disjunctive normal form)이라고 합니다. DNF 식을 참으로 만들 수 있는지 판별하는 것은 코드포스 Div2B 문제로도 나온 적 있는 쉬운 문제이지만, 그 경우의 수를 세는 것은 #P-완전입니다. (힌트: 카운팅 SAT에서 환원해 보세요!)

흥미롭게도, 이분 그래프의 완전 매칭의 개수 자체에 비례하는 시간 복잡도로 완전 매칭의 개수를 세는 알고리즘이 있습니다. 물론 그 개수가 최대 $n!$이므로 다항 시간은 아닙니다.⁵ 여기에 추가로 소개하기에는 이 글이 이미 어렵고, 따로 소개하기에는 내용이 적으므로 생략합니다.

참조 문헌