Consistent Hashing
안녕하세요?
오늘은 웹서버 등에서 요청을 여러 곳으로 공평하게 분산시키는, load balancing 작업을 수행할 때 널리 사용되는 consistent hashing 알고리즘에 대해 알아보겠습니다.
Consistent hashing은 1997년 Karger의 논문 Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web에서 제안된 알고리즘입니다.
서론
Karger의 논문에서는, 다른 클라이언트에서 접근 가능한 많은 object를 가지고 있는 단일 서버의 상황을 가정하였습니다.
서버에 캐시를 두면 더 빠른 접근이 가능하다는 것은 자명합니다. Object들은 여러 개의 캐시에 분산되어야 하는데, 여러 개의 캐시를 두었을 때 각 캐시가 비슷한 양의 object들을 가지고 있어야 합니다. 또, 어떤 object가 어떤 캐시에 저장되어 있는지를 알아야 합니다.
가장 쉽게 생각할 수 있는 방식은 해시를 사용하는 것입니다. 총 p개의 캐시가 있을 때, h(x) % p의 값에 따라 캐시를 구분지어 사용하면 캐시에 고른 양의 object들을 분산시킬 수 있습니다.
하지만 캐시의 정보, 예를 들면 서버에서 사용할 수 있는 캐시의 수가 변경된다면 어떻게 될까요? 이 경우, 변경에 따라 h(x) % p와 같은 기준을 통해 캐시를 구분하였다면 대부분의 object들이 새로운 위치로 변경되어야 합니다.
즉, 변경이 일어날 때마다 캐시가 가지고 있는 대부분의 데이터가 쓸모없게 변하는 것입니다. 이러한 문제를 해결하기 위하여 consistent hashing의 개념이 도입되었습니다. 보다 엄밀히, consistent hashing이 추구하는 목표는 아래와 같습니다.
1) smoothness peoperty
새로운 machine이 추가되거나 삭제될 때, 캐시들의 balance를 유지하기 위해 옮겨져야하는 object들의 기댓값은 최소여야 합니다
2) spread peoperty
개체가 할당되는 서로 다른 캐시의 수는 적게 유지되어야 합니다.
3) load peoperty
하나의 캐시에 할당된 object들의 수는 적게 유지되어야 합니다
Consistent Hashing
위 조건들은 아래와 같이 조금 더 엄밀하게 나타낼 수 있습니다.
I는 mapping될 item들의 집합, B는 bucket의 집합이라고 하겠습니다. ranged hash function f(V, i)는 아이템 i를 view V(view란 bucket의 subset 중 하나를 뜻합니다) 중 하나의 bucket으로 mapping시키는 함수라고 합시다.
위에서의 조건은 다음과 같이 정의될 수 있습니다.
1) smoothness(=balance) property
어떠한 view V가 주어졌을 때, hash family에서 랜덤하게 골라진 함수에 대해 어떤 item이 하나의 bucket으로 mapping될 확률은 최대 $O(\frac{1}{|V|})$이다.
2) spread peoperty
$V_1, V_2, …, V_v$의 view들의 집합에 대해, 하나의 item i에 대해 spread(i)는 $|f_{V_j}(i)|$, j=1 to v로 정의합니다.
3) load peoperty
하나의 bucket b에 대해, load(b)는 $|f_{V}^{-1}(b)|$로 정의됩니다. 다시 말해, 해당 bucket에 mapping되는 item의 수입니다.
구현
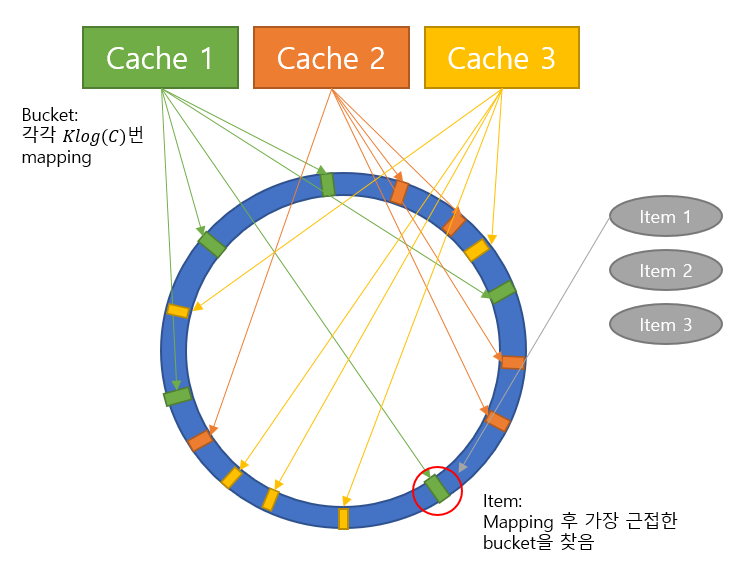
해시를 통해 mapping되는 unit interval을 구간 [0, 1]이며, 1과 0이 서로 인접한 링 모양이라고 가정합시다.
어떠한 해시함수 $h_b(x)$를 사용해, 어떠한 상수 K에 대해 하나의 bucket을 Klog(C)번 mapping하고,
또다른 해시함수 $h_i(x)$를 사용해, 하나의 item을 매핑합니다. 여기서 C는 시스템에서 가질 수 있는 최대 캐시의 개수입니다.
이제 ranged hash function $f_V(i)$를 i를 mapping하였을 때 하나의 bucket $b \in V$를 return하는 해시함수이며, i의 해시값과 가장 가까운 값을 반환하는($|h_i(x) - h_b(x)|$를 최소화하는) 해시함수라고 가정합시다.
아래 그림은 consistent hashing의 전체적인 작동을 나타낸 그림입니다.
시간 복잡도
가장 먼저 각 bucket을 mapping시켜야 합니다. 총 V개의 bucket이 있으며, 하나의 bucket 당 Klog(C)회 해시 함수를 구해야 하니 총 $O(V\log{C})$만큼의 연산이 필요합니다.
이제 하나의 아이템마다 어떠한 bucket에 mapping되어야 하는지를 알아야하기 때문에, 이는 balanced binary search tree를 사용해 구현 가능합니다. 총 $KV\log{C}$개의 구간이 있으므로, 하나의 item에 대한 매칭되는 bucket을 찾으려면 $O(\log{(C\log{C})})$만큼의 시간이 소요됩니다.
논문에서 제시하는 hashing을 위한 시간을 조금 더 줄이는 방법으로는, unit interval을 $KC\log{C}$개의 구간으로 나누어 놓는 것입니다. 자명하게도, 이럴 경우 O(1)에 해싱을 완료할 수 있습니다.
구현상의 편의점으로, 원본 논문에서는 $|h_i(x) - h_b(x)|$를 최소화하는 bucket을 구했지만, $h_i(x) \le h_b(x)$가 되는 최소의 bucket을 찾아도 복잡도에는 크게 영향이 없습니다. 이 경우, lower_bound를 찾는 것으로 대체가 가능합니다. 많은 구현에서는 해당 bucket을 찾는 것으로 대체하는 경우가 많았습니다.
다음으로 bucket을 추가하거나 삭제하는 연산에 대해 알아보도록 하겠습니다.
하나의 bucket을 추가할 경우, 해당 bucket 또한 총 $K\log{C}$회 mapping이 일어나게 되어, 총 $3K\log{C}$개의 새로 생기거나 변화된 구간이 생겨나게 됩니다. 하나의 segment에는 $O(1)$개의 item이 존재한다고 기대할 수 있으며, 하나의 hash에 소모되는 시간은 $O(1)$이기 때문에 총 걸리는 시간은 $O(\log{C})$가 됩니다.
마지막으로 하나의 bucket을 삭제하는 경우를 살펴보도록 하겠습니다. 하나의 bucket을 삭제하는 경우는 위와 거의 유사한데, 변화되는 구간의 수가 $3K\log{C}$개에서 $2K\log{C}$개로 바뀝니다. 상수 외에 달라지는 것은 없으므로 마찬가지로 총 소요시간은 $O(\log{C})$입니다.
Reference
아래는 글을 작성하는 데에 참고한 논문입니다.