비지도 방식으로 GANs의 이미지 생성을 조작하는 방법
소개
GANs는 이미지 생성이나 스타일 변화 테스크에서 굉장한 성능을 보여주고 있습니다. 특히, StyleGAN, BigGAN과 같은 최신 모델은 이미 실제와 구분이 힘들정도로 자연스러운 이미지를 생성합니다. 유저가 아웃풋 이미지를 원하는 형태로 조절하는 연구 또한 많이 진행되었으나 대부분 추가적인 라벨을 사용해서 모델을 학습하는 것에 초점을 맞췄었습니다.
GANs의 해석 가능성에 대한 연구가 활발해지면서 각 특징을 조작하는 변수가 잘 구분되도록 학습하는 테스크인 disentanglement learning이 주목받게 됩니다. InfoGAN, beta-VAE 등이 대표적인 모델로 비지도 방식으로 생성 모델을 학습하면서 출력 결과의 중요한 특징들을 독립적인 latent factor들로 표현할 수 있게 만듭니다. 하지만, 이러한 모델들로 이미지를 생성하면 오브젝티브에서 disentanglement와 reconstruction 퀄리티 사이의 trade-off를 설정하게 되어 있기 때문에 순수하게 이미지 생성을 목표로 하는 모델에 비해서는 생성 이미지 퀄리티가 떨어질 수 밖에 없습니다.
이미지 퀄리티를 해치지 않게 조금 다른 방향으로 문제를 해결해볼 수도 있는데요. 대략적인 방법은 다음과 같습니다.
- 모델을 좋은 퀄리티의 이미지 생성하도록 오브젝티브를 두고 학습합니다.
- 학습한 모델의 파라미터를 고정하고 latent space에서 이미지를 조작 가능하게 하는 방향을 찾습니다.
- 찾은 방향으로 perturbation을 주어 이미지를 생성합니다.
찾은 방향으로 perturbation을 주어서 이미지를 생성하면 한 특징만 변하는 연속적인 이미지를 얻을 수 있고, 동시에 모델을 수정하지 않았기 때문에 이미지의 퀄리티를 보장할 수 있게 됩니다. 최근 이와 비슷한 접근을 하는 여러 연구들이 눈에 띄는 결과(demo)를 보여주는 것 같아서 몇 가지 소개해보고자 합니다.
Unsupervised Discovery of Interpretable Directions in the GAN Latent Space
“Unsupervised Discovery of Interpretable Directions in the GAN Latent Space”는 ICML2020에 accept된 논문으로 GANs의 latent space에서 disentagled한 벡터(interpretable direction) 집합을 비지도 방식으로 찾는 방법을 소개합니다.
방법
interpretable direction을 찾기 위해 학습된 이미지 생성 모델의 파라메터를 고정시키고 행렬 A와 reconstructor R을 학습합니다. 여기서 A의 각 컬럼은 interpretable direction들의 후보를 나타냅니다.
먼저, 기준이 되는 이미지에 대응될 latent code $z$를 standard multivariate normal 분포에서 샘플링합니다. 그리고 $z$에서 특정 방향으로 쉬프트한 latent code 값 $z+A(\epsilon e_k)$을 계산합니다. 여기서 $e_k$와 $\epsilon$은 샘플링한 값으로 $e_k$는 $A$의 컬럼 벡터들 중 어떤 것을 선택할지 정하는 원 핫 벡터이고 $\epsilon$은 해당 방향으로 변화 시키는 정도를 나타냅니다. 생성된 각 latent code를 이미지 생성 모델 $G$에 입력하여 이미지를 생성하면 reconstructor $R$은 이 두 이미지를 바탕으로 latent code 상에서 변화된 방향과 정도의 추정 값 $\hat{k}$, $\hat{\epsilon}$을 계산합니다.
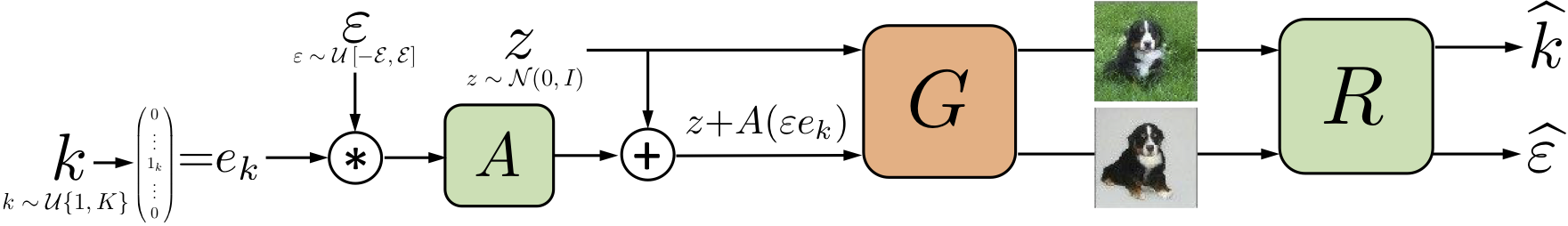
모델은 다음과 같은 오브젝티브를 가지고 학습됩니다. 여기서 $L_{cl}$, $L_r$ 은 각각 cross-entropy 함수와 mean absolute error를 나타냅니다. 로스를 감소시키는 방향으로 학습이 진행되면 $A$의 컬럼 벡터가 $R$에 의해 쉽게 구분될 수 있는 형태가 됩니다. 저자의 실험에 의하면 이렇게 해서 얻어진 $A$의 컬럼 벡터들은 disentangled하고 대게 human-interpretable하다고 합니다.
\[\min_{A,R}\mathbb{E}_{z,k,\epsilon}[L_{cl}(k,\hat{k}) + \lambda L_r(\epsilon, \hat{\epsilon})]\]저자는 실험에서 $A$가 일반 행렬인 경우, 열벡터가 단위 길이인 경우, orthonormal한 경우에 대해서 실험을 해보았습니다. 첫 번째 경우에는 $A$의 컬럼 벡터가 높은 $l_2$ norm 값을 갖게 되어 쉬프트된 생성이미지가 비슷하게 되는 문제가 있었다고 합니다. 그래서 두 번째와 세 번째 조건 하에서 $A$를 학습시켰고 두 번째 경우가 대체로 더 다양한 interpretable direction을 내놓았다고 합니다.
결과
아래는 저자가 찾은 interpretable direction 예시입니다. latent space에서 회전, 배경이 blur한 정도, 자연스러움 정도 등을 다양한 데이터 셋에서 조절 가능할 수 있는 방향을 찾는 데 성공했습니다.

의견
-
생성 모델의 이미지 퀄리티를 낮추지 않고 원하는 개수만큼의 interpretable direction을 얻을 수 있는 직관적인 방법인 것 같습니다.
-
$A, R$ 학습시 validation이 어려워서 오버피팅을 감지하기 어려워 보입니다. 논문에는 자세하게 나오지 않았는데 training step을 어떻게 정할 수 있을지 궁금하네요.
Ganspace: Discovering interpretable gan controls
“Ganspace: Discovering interpretable gan controls”는 NeurIPS 2020에 accept된 논문으로 latent space에서 PCA를 활용해 StyleGAN, BigGAN 모델의 이미지 생성을 조작하는 방법을 소개합니다.
방법
PCA를 어떻게 적용할지 설명하기 앞서 일반적인 생성 모델의 구조를 수식화해봅시다. $z$를 $p(z)$로부터 샘플한 노이즈 벡터라고 하면 생성모델 $G$는 $z$로부터 출력 이미지 $I=G(z)$를 생성합니다. $G$는 $L$개의 중간 레이어 $G_1, …, G_L$로 분해될 수 있습니다. 첫 번째 레이어는 입력 값인 $z$로부터 $y_1=G_1(z)$를 생성하고 $i=2,..,L$번째 레이어는 $y_{i-1}$로부터 $y_i=\hat{G}i(z)=G_i(y{i-1})$를 생성합니다. 이때, 마지막 레이어의 출력 값은 RGB image인 $I=G_L(y_{L-1})$가 됩니다.
BigGAN은 중간 레이어에 $z$와 클레스 벡터가 입력값으로 들어가는데 실험에서 클레스 벡터를 고정하므로 $y_i=G_i(y_{i-1}, z)$로 표현합니다. StyleGAN은 첫 번째 레이어에서 상수 $y_0$를 입력받습니다. 중간 레이어는 $z$를 뉴럴넷 $M$를 통과시켜 얻은 값 $w=M(z)$를 추가로 입력받아서 $y_i=G_i(y_{i-1}, w)$로 표현합니다.
StyleGAN에서는 이미지를 조작하기 위해서 $w$의 주성분을 계산합니다. 이를 위해 $z$로부터 $N$개의 샘플 벡터 $z_1, z_2, …, z_N$을 얻고 $w_i=M(z_i)$, $i=1,2,…,N$의 PCA를 계산합니다. 이때 얻어지는 basis 행렬을 $V$라고 할 때 컨트롤 파라미터 $x$에 대한 이미지는 $w$ 대신에 $w’=w+Vx$를 사용하여 생성합니다.
BigGAN은 StyleGAN과 같이 변수 $w$가 없으므로 조금 다른 방법으로 PCA를 구합니다. $i$번째 레이어에 PCA를 하는 경우, $y_j=\hat{G}i(z_j), j=1,2,…,N$의 PCA를 계산합니다. 이때 얻어지는 basis 행렬을 $V$, data 평균을 $\mu$라고 할 때, PCA 좌표값 $x_j$는 $x_j=V^T(y_j-\mu)$가 됩니다. 컨트롤 할 방향을 결정하는 행렬 $U=\argmin \sum{j}\lVert Ux_j-z_j \rVert^2$를 구하고 컨트롤 파라미터 $x$에 대한 이미지는 $z$ 대신에 $z’=z+Ux$를 사용하여 생성합니다.

저자는 생성 모델의 특정 레이어만 수정(layerwise edit)해서 다양한 방식으로 이미지 생성을 조작할 수 있음을 확인했습니다. StyleGAN의 경우 특정 구간에 있는 레이어에 대해서만 $w$를 principle component 방향으로 수정했습니다. BigGAN은 skip-$z$ 입력을 변형해서 StyleGAN과 비슷하게 조작할 수 있다고 합니다.
결과
아래는 StyleGAN과 BigGAN의 layerwise edit을 한 결과입니다. $E(x, y-z)$는 $y,…,z$번 레이어에서 컨트롤 변수를 $x$방향으로 수정한 경우를 의미합니다.

의견
-
논문의 방법이 잘 적용되기 위해서는 PCA를 적용할 latent space에서 semantic label을 공유하는 점들이 주성분 방향으로 배치되어야 합니다. StyleGAN을 비롯한 대부분의 최신 모델들은 학습시 피쳐를 어느 정도 disentangled하게 만드는 과정이 있어서 이 가정을 적용할 수 있을지 몰라도 그렇지 않은 경우(ex. vanilla GANs)에는 논문의 방법이 잘 적용될지 확인해야 할 것 같습니다.
-
principal component의 독립성은 데이터가 multivariate gaussian 분포일 때 성립합니다. 따라서 latent space 상에서 점들의 분포가 이와 크게 다르면 principal component가 더이상 유의미한 조작 방향이 아니게 될 것 같습니다.
Closed-Form Factorization of Latent Semantics in GANs
“Closed-Form Factorization of Latent Semantics in GANs”은 홍콩과기대에서 쓴 논문입니다. 이 논문은 모델을 학습하거나 샘플링을 하지않고 projection을 분해해서 latent direction을 찾는 방법을 소개합니다.
방법
여태까지 논문들이 이미지를 수정할 때 사용한 공통적인 방식을 살펴봅시다. latent space에서 처음 이미지의 latent code가 $z$이고 특정 방향 $n$과 해당 방향으로 변화시킬 강도 $\alpha$가 주어졌을 때 이미지 수정은 다음과 같이 이루어집니다. $\text{edit}(G(z)) = G(z’) = G(z+\alpha n)$
GANs의 생성 모델은 latent space에서 image space까지 반복적으로 projection을 하는 형태로 볼 수 있는데요. 첫 번째 projection을 아핀 변환으로 근사해서 식을 정리해봅시다.
$y’=G_1(z’)=G_1(z+\alpha n)=Az+b+\alpha An = y + \alpha An$
이 식 형태에서 알 수 있는 점은 이미지의 변화가 latent code $z$와는 상관없고 $\alpha An$값에 의존한다는 점입니다. 또한, 그래서 $A$의 가중치가 이미지 변화에 필수적인 정보를 가지고 있다고 예상할 수 있습니다. 직관적으로 $\lVert A{n_i}\rVert=0$인경우 $y’=y$가 되므로 이미지가 변하지 않게 되니까 반대로 $\lVert A{n_i}\rVert$를 크게 만들어주는 $n_i$을 찾으면 되지 않을까 생각할 수 있습니다.
이를 바탕으로 저자는 다음과 같은 문제를 풀 것을 제안합니다.
$N^\ast = \argmax_{N\in\mathbb{R}^{d\times k}: n_i^Tn_i=1 \forall i = 1,\cdots,k} \sum_{i=1}^k \lVert A{n_i}\rVert_2^2$
저자는 라그랑지안을 사용해서 $A^TA$에서 가장 큰 $k$개의 eigenvalue 각각에 대응되는 eigenvector가 $n_1,\cdots,n_k$의 해가 됨을 보였습니다. 저자는 PGGAN, StyleGAN, BigGAN에 대해 일부 projection을 분해하고 앞의 방식대로 latent code를 수정하여 이미지를 생성했습니다.
결과
아래는 다양한 데이터 셋과 모델에서 저자의 방법으로 이미지를 수정한 결과입니다.

의견
- 위 $N^\ast$ 식은 논문 식을 그대로 옮긴건데 $n_i$들이 선형 독립이라는 조건이 추가되어야 할 것 같습니다.
- 실은 위 문제가 Rank-$k$ 근사 문제와 동치라서 가장 큰 $k$개의 singular value에 대응되는 $A$의 right singular vector가 답이 됩니다.
마치며
이 주제는 정량 평가나 메소드간 공정한 비교를 하기 굉장히 어려운 것 같습니다. 그래서 대부분 유저스터디나 매우 많은 정성 결과로 주장을 뒷받침하는 것 같습니다. 메소드 간 성능을 어떻게 최대한 정량적으로 분석할 수 있을지 고민해보면 좋을 것 같습니다. 아래는 논문을 읽으면서 느꼈던 실험시 고려해야 할 점을 적었습니다.
- 메소드, 랜덤 시드마다 컨트롤 할 수 있는 semantic이 다르게 나올 수 있다.
- 어떤 조작이 human-interpretable, disentangled 한지 명확한 정의가 필요하다.
- 라벨링 cost와 비교하기 위해 메소드가 유의미한 조작을 얼마나 쉽게 찾을 수 있는지(가령 빈도라던가) 기술해야 한다.
- 메소드가 어느 범위의 모델까지 적용할 수 있는지 기술해야 한다.(예를 들어, 특정 GAN 혹은 모든 GAN)