Multi-Party Computation 1
1. Introduction
두 부자 Alice와 Bob이 있다. 두 명은 상대방에게 자신의 재산이 얼마인지 공개하지 않고 누구의 재산이 더 많은지 비교하고 싶다.
라는 문제를 생각해봅시다. 사실 이 문제를 해결하는 방법은 굉장히 간단합니다. Alice와 Bob이 모두 신뢰할 수 있는 Charlie가 있다면 Alice와 Bob이 Charlie에게 자신의 재산을 알려주고 Charlie가 비교를 한 후 누가 더 재산이 많은지를 두 사람에게 알려주면 됩니다.
하지만 두 사람이 모두 신뢰할 수 있는 제 3자가 없다면 상황이 많이 복잡해집니다. 결국 대소를 비교하려면 양쪽의 값을 누군가는 알아야할 것 같은데 상대방에게 자신의 재산이 얼마인지 공개하지 않는다는 조건이 있기 때문에 그럴 수는 없습니다.
이 문제는 Yao’s Millionaire’s Problem이라는 이름이 붙어있는 문제로, 1982년 Andrew Yao가 제시한 문제입다다.
이 문제를 일반화하면 Alice는 입력 $x$를, Bob은 입력 $y$를 들고 있을 때 $f(x, y)$를 계산하되 Alice는 $y$를, Bob은 $x$를 알 수 없어야 합니다. 이러한 상황을 Multi-Party Computation(MPC)라고 부르고, 나름대로 쓰임새가 있는 알고리즘입니다. 대표적인 에시를 1개만 제시해보면 Privacy Preserving Machine Learning을 예로 들 수 있습니다.
최근 AI 챗봇과 관련한 논란에서 알 수 있듯 현재의 머신 러닝 환경에서는 회사가 개인의 정보를 습득할 수 있습니다. 이를 방지할 수 있는 방법 중 하나로 서버에서 계산을 하는 대신 개인의 디바이스에서 계산을 하는 방법이 있지만 이 경우에는 반대로 회사 입장에서 비싼 비용을 들여서 훈련을 시켜 만들어둔 모델이 model extraction attack과 같은 방법으로 노출된다는 부작용이 있습니다. 결국 여기서 이루어지는 계산도 회사가 설정해준 parameter와 개인의 입력을 조합해서 결과를 내는 방식이니 Multi Party Computation을 이용해 개인의 민감한 데이터가 회사에게 노출되지 않고, 회사가 비용을 들여서 얻어낸 parameter도 개인에게 노출되지 않을 수 있습니다.
Multi-Party Computation을 수행할 수 있는 다양한 방법이 있는데 그 중에서 Garbled Circuit에 대해 처음의 등장과 이후의 발전을 서술해보겠습니다.
2. Oblivious Transfer
Garbled Circuit에 대해 논의를 하기 전에 Garbled Circuit에서 필수로 사용되는 Oblivious Transfer를 설명드리겠습니다.
Oblivious Transfer는 아래와 같은 기능을 제공하는 프로토콜입니다.
- Alice는 $m_0, m_1$을 정합니다.
- Bob은 $b \in {0, 1}$을 정합니다.
- Bob은 $m_b$를 알아내지만 $m_{1-b}$에 대해서는 아무런 정보를 얻지 못합니다.
- Alice는 Bob이 $m_0$과 $m_1$ 중에서 어떤 것을 가져갔는지 알지 못합니다.
말 그대로 Alice는 2개의 정보를 양 손에 쥔 채로 내밀고 있고, Bob은 그 중에서 자신이 원하는 1개를 택해서 가져가는데 대신 자신이 택하지 않은 것에 대한 정보는 얻지 못해야 하고 또 Alice는 Bob이 무엇을 가져갔는지를 알 수 없어야 합니다.
이 프로토콜 또한 어떤 식으로 구현을 해야 하나 조금 당황스럽겠지만 공개키 암호 시스템을 이용해서 그렇게 어렵지는 않게 구현할 수 있습니다. Oblivious Transfer을 어떤 식으로 구현할 수 있는지보다는 이를 사용해서 Garbled Circuit을 수행하는 과정에 더 관심이 있기 때문에 Rabin encryption을 이용한 간단한 형태의 Oblivious Transfer만 익히고 가겠습니다.
Rabin encryption을 이용한 Oblivious Transfer는 아래와 같습니다.
- Alice는 Bob에게 전달할 $m_0, m_1$을 정합니다.
- Alice는 RSA key pair $N, e, d$를 정하고 $N, e$를 Bob에게 알려줍니다.
- Alice는 랜덤값 $x_0, x_1$을 정해 Bob에게 알려줍니다.
- Bob은 랜덤값 $k$와 $b$를 정합니다. $b$는 Bob이 전달받고 싶은 메시지가 $m_b$임을 의미합니다.
- Bob은 $v = (x_b + k^e) \mod \ N$을 계산한 후 Alice에게 $v$를 넘겨줍니다. Alice는 $k$를 모르기 때문에 $v$로부터 $x_b$를 알 수 없습니다.
- Alice는 $k_0 = (v-x_0)^d \mod \ N$과 $k_1 = (v-x_1)^d \mod \ N$을 계산합니다. $k_b$는 $k$와 일치하지만 Alice는 무엇이 $k$와 일치하는지 알 수 없습니다.
- Alice은 $m’_0 = m_0 + k_0$과 $m’_1 = m_1 + k_1$을 계산한 후 둘을 Bob에게 넘겨줍니다.
- Bob은 $m_b = m’_b - k$를 계산해 $m_b$를 알 수 있습니다.
이와 같이 우리는 Oblivious Transfer를 만들 수 있습니다. 엄밀히 말해 지금 제시한 Oblivious Transfer는 2개 중에서 1개를 고르는 1-out-of-2 Oblivious Transfer이고 n-out-of-m Oblivious Transfer로 확장이 가능하지만 Garbled Circuit 에서는 1-out-of-2만 쓰이기 때문에 여기까지만 설명을 하겠습니다.
3. Garbled Circuit
(이 챕터에서 사용된 그림은 Mike Rosulek, Oregon State University의 A Brief History of Practical Garbled Circuit Optimizations Workshop의 슬라이드에서 가져왔습니다.(Workshop 링크))
드디어 Garbled Circuit에 대해 알아보겠습니다. 우선 우리의 목표를 다시 한 번 적어보면 Alice는 입력 $x$를, Bob은 입력 $y$를 들고 있을 때 $f(x, y)$를 계산하되 Alice는 $y$를, Bob은 $x$를 알 수 없어야 합니다.
이 때 우리는 어떤 함수 $f$를 아래와 같이 회로로 나타낼 수 있습니다.
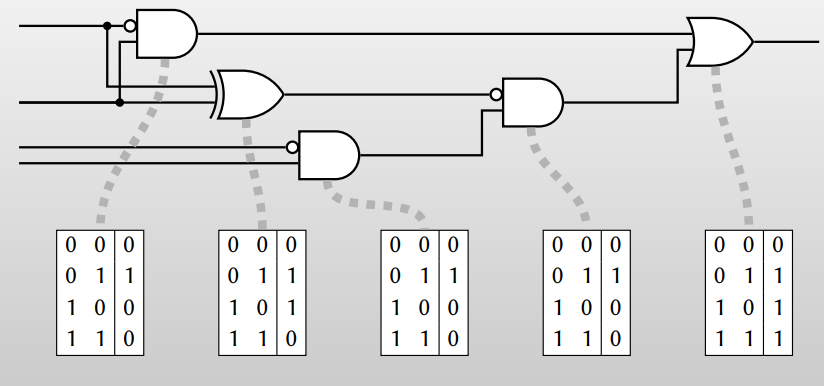
그러면 우리는 XOR, AND, OR, NOR와 같은 각 gate를 어떻게 처리할지 생각해보면 됩니다. 특히 XOR, AND gate만 처리할 수 있으면 나머지는 비슷한 방법으로 처리가 가능하기 때문에 이 글에서는 XOR, AND gate에 대해서 설명을 드리겠습니다.
Garbled Circuit에 참여하는 2명은 미리 연산에 필요한 값들을 정해두는 Garbler와 Garbler로부터 제한된 값을 받아 연산을 수행하는 Evaluator로 역할이 나누어집니다. Evaluator는 연산을 수행한 후 결과를 Garbler에게 알려줍니다. Yao’s Millionaire’s Problem으로 설명을 해보면 Garbler는 자신의 재산을 값은 노출되지 않는 어떠한 형태로(구체적인 방법은 후술할 예정입니다.) Evaluator에게 알려주고 Evaluator는 계산을 마친 후 결과를 Garbler에게 알려줍니다.
Garbled Circuit은 semi honest 환경을 가정합니다. semi honest 환경이란 Garbler와 Evaluator가 주어진 각자의 역할을 충실하게 수행하되 공격을 하고자 하는 환경을 말합니다. 즉 프로토콜에 참여하면서 Evaluator는 Garbler의 입력을 알아내고 싶어하지만 계산 중간에 값을 임의로 변조한다던가, 계산을 마친 후 결과를 알려주지 않는다거나 하는 active attack을 하지 않습니다.
지금부터 Garbled Circuit을 어떻게 구현할 수 있는지 맨 처음 제시된 가장 기초적인 형태를 알아보고 어떤 식으로 발전이 이루어졌는지 알아보겠습니다.
A. Yao’s version
지금 소개할 버전은 가장 초기의 Garbled Circuit입니다. 아래의 그림을 보면서 논의를 이어갑시다.
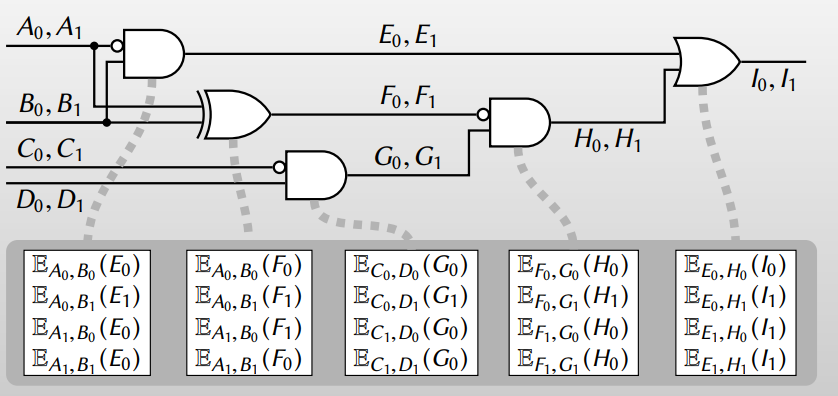
Garbler는 각 wire에 일정 길이(e.g. 80-bit, 128-bit) 랜덤값 2개를 정합니다. $A_0, A_1$을 예로 들면 $A_0$은 해당 wire에서의 0에 대응되고 $A_1$은 1에 대응됩니다. 그림의 회로에서는 $A, B, C, D$가 입력이고 $I$가 출력입니다. 편의상 $A, B$는 Garbler의 입력, $C, D$는 Evaluator의 입력이라고 가정해봅시다. 그러면 Garbler는 자신의 입력에 대응되는 $A_0$ 혹은 $A_1$, 그리고 $B_0$ 혹은 $B_1$을 Evaluator에게 알려줍니다. 만약 A가 1이고 B가 0이었다면 Garbler는 Evaluator에게 $A_1, B_0$을 알려주게 됩니다. 단 이 때 Evaluator는 자신이 받은 랜덤값이 $A_0$인지 $A_1$인지는 알 수 없습니다. 그리고 $C, D$는 Oblivious Transfer를 이용해 Evaluator에게 넘겨줍니다. C가 0이고 D가 1이었다면 Evaluator는 Oblivious Transfer를 통해 $C_0$과 $D_1$을 받게 됩니다. Oblivious Transfer의 특성상 Garbler는 Evaluator의 입력인 $C, D$ 값을 알 수 없습니다. 그리고 Evaluator는 자신이 가져간 $C_0, D_1$만 알고 $C_1$ 혹은 $D_0$을 알 수 없습니다.
그리고 그림에서 하단에 있는건 각 gate에 대응되는 테이블을 의미합니다. 테이블에서 $\mathbb{E}_{A_0, B_0}(E_0)$이 의미하는 바는 키 $A_0, B_0$으로 평문 $E_0$을 암호화한 결과를 의미합니다. 이 때 암호 시스템 $\mathbb{E}$는 올바르지 않은 키로 복호화를 시도할 경우 에러를 반환해야 합니다. 즉 인증(Authentication) 기능이 추가로 들어있는 암호 시스템이어야 합니다. 이 테이블은 Garbler가 생성하고 Evaluator에게 넘겨줍니다. 테이블이 왜 저런 형태인지를 이해하기 위해 맨 처음 !A and B를 수행하는 AND gate를 보면 A가 0이고 B가 1일 때에만 결과가 1이고 나머지는 0이어야 합니다. 그렇기 때문에 테이블에서 $A_0, B_1$에 대응되는 값만 $E_1$이고 나머지는 $E_0$입니다. 그리고 테이블에 있는 4개 원소의 순서는 랜덤이어야 합니다.
이제 Evaluator는 처음 입력을 가지고 gate를 위상 순으로 계산해나가면 됩니다. 예를 들어 $A_1$과 $B_0$을 받았다면 해당 gate에 대응되는 테이블을 참고해 암호문 4개를 전부 키 $A_1, B_0$으로 복호화해봅니다. 4개 중 대응되는 1개만 복호화가 정상적으로 이루어져서 $E_1$이라는 결과를 낼 것입니다. Evaluator는 이 값이 $E_0$에 대응되는지 $E_1$에 대응되는지 알 수 없지만 계산을 계속 이어나가는 데에는 아무 문제가 없습니다. 최종적으로 $I_0$ 혹은 $I_1$ 값을 얻으면 이를 Garbler에게 알려주고, Garbler는 그 값을 보고 최종 결과가 0인지 혹은 1인지를 Evaluator에게 알려줍니다.
이 방식대로면 Multi Party Computation을 수행할 수 있지만 Evaluator가 각 gate에서 복호화를 4번 수행해야 하고 암호 시스템이 인증 기능을 제공해야 한다는 단점이 있습니다.
B. Point-and-permute
Point-and-permute는 1990년 D. Beaver, S. Micali, and P. Rogaway. 1990. The round complexity of secure protocols. 논문에서 소개된 방법입니다. 이 방법 아래에서는 암호 시스템이 인증 기능을 제공하지 않아도 됩니다.
아이디어는 간단합니다. 각 wire에서 두 값의 lsb를 다르게 할당합니다. 즉 $A_0$의 lsb는 0인데 $A_1$의 lsb는 1이거나, $A_0$의 lsb는 1인데 $A_1$의 lsb는 0으로 둡니다. 그리고 이 lsb의 값에 따라 테이블의 원소들을 배치합니다. 아래의 그림에서는 빨간색과 파란색 점이 lsb를 의미합니다.
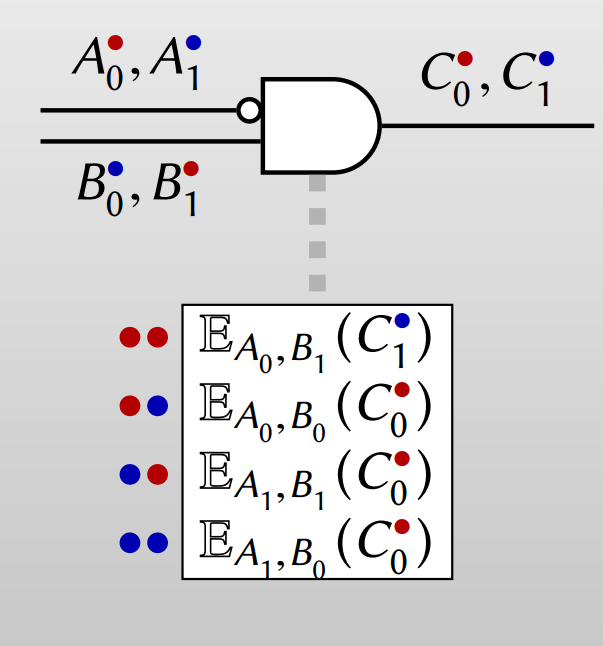
이렇게 되면 Evaluator의 입장에서 복호화를 4번 수행하는 대신 바로 자신이 복호화를 해야하는 값이 무엇인지를 알 수 있기 때문에 복호화를 1번만 하면 되고 암호 시스템 또한 인증 기능을 제공할 필요가 없어집니다.
C. Garbled Row Reduction
Garbled Row Reduction은 1999년 Moni Naor, Benny Pinkas, and Reuban Sumner. 1999. Privacy preserving auctions and mechanism design. 논문에서 소개된 방법입니다. Point-and-permute를 통해 Evaluator의 복호화는 1번으로 줄었지만 Garbler가 각 gate에서 4개의 암호문을 Evaluator에게 보내줘야 함은 여전합니다. 이 때 wire의 랜덤값을 적절하게 둬서 3개의 암호문을 보내도록 할 수 있습니다. 방법은 바로 Point-and-permute에서 제일 위에 위치한 암호문의 값이 0이 되도록 만드는 방법입니다.
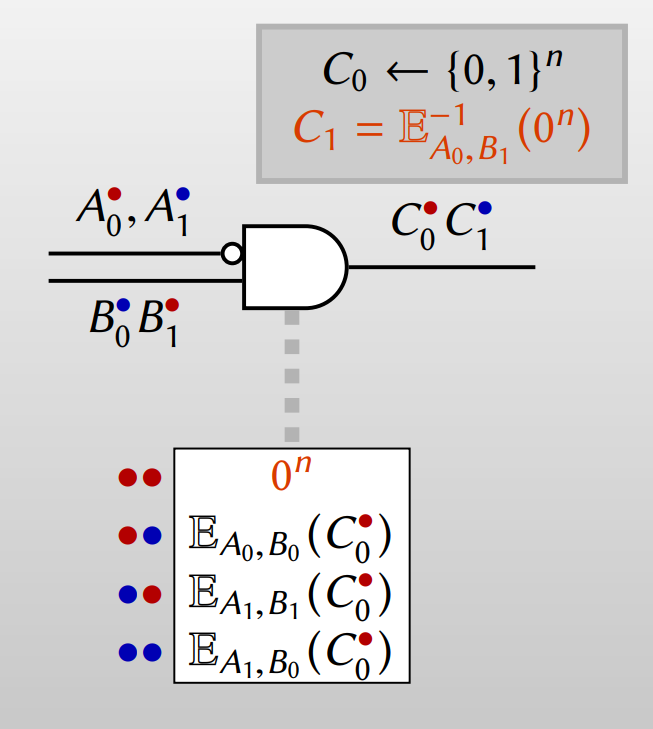
$C_0, C_1$ 둘 다 랜덤으로 정하는 대신 $C_0$은 랜덤으로 정하고 $C_1$은 제일 위에 위치한 암호문의 값이 0이 되도록 정하면 Garbler는 Evaluator에게 3개의 암호문만 보내주면 됩니다.
D. Free XOR
지금까지는 AND와 XOR이 아무런 차이가 없었습니다. 그런데 2008년 Kolesnikov V., Schneider T. (2008) Improved Garbled Circuit: Free XOR Gates and Applications. 논문에서 소개된 방법을 통해 AND와 달리 XOR는 Garbler, Evaluator의 암호화/복호화 연산을 필요로 하지 않은채로 계산을 할 수 있게 되었습니다.
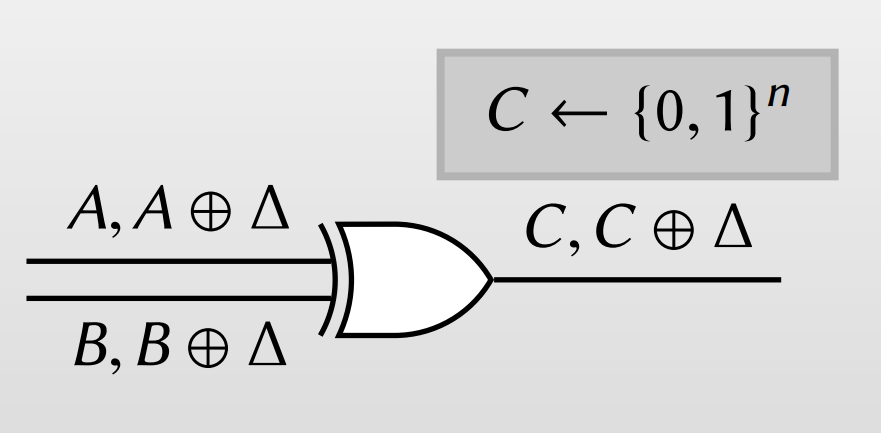
Garbler는 $\Delta$를 정한 후 각 wire에서 $A_0$, $A_1$을 랜덤으로 정하는 대신 둘 중 어느 하나는 랜덤으로 정하고 $A_0 \oplus A_1 = \Delta$가 만족하도록 값을 둡니다. 그러면 Evaluator의 입장에서 XOR을 수행할 때 암호문을 가지고 복잡한 처리를 하는 대신 $C = A \oplus B$를 수행해서 바로 XOR에서 출력 wire에 대응되는 값을 알 수 있습니다.
만약 $\Delta$를 Evaluator가 알게 된다면 연산 중간에 반대편 wire의 값을 너무나 쉽게 알아낼 수 있게 됩니다. 그렇기 때문에 Evaluator가 특정 wire에서 $W_0, W_1$을 모두 아는 일은 없어야 하고 실제로 Garbled Circuit에서는 그러한 일이 발생하지 않습니다.
E. Half Gates
드디어 4번의 진화를 거쳐 최종적인 형태에 진입했습니다. 2015년 Zahur S., Rosulek M., Evans D. (2015) Two Halves Make a Whole. 논문에서 소개된 방법을 통해 AND에 대응되는 gate당 2개의 암호문을 필요로 하도록 만들 수 있습니다. 이 방법이 현재까지 알려진 가장 좋은 방법입니다.
우선 XOR은 Free XOR에서 소개한 방법을 그대로 가져다 씁니다. 그리고 AND에서 Evaluator가 필요로 하는 암호문의 수를 줄이기 위해 AND를 2번에 나누어서 진행합니다.
우선 $a and b = (a \oplus r \oplus r) \ and \ b = [(a \oplus r) \ and \ b] \oplus [r \ and \ b]$입니다. 그리고 $r$을 $A_0$의 lsb라고 둔다면 Garbler는 $r$을 알고 Evaluator는 $a \oplus r$을 압니다. Garbler가 $r$을 아는건 당연하고 Evaluator가 왜 $a \oplus r$를 알 수 있는지 생각해보면 Evaluator가 $A_0$인지 $A_1$인지 모를 $A$를 받았을 때 $A$의 lsb가 바로 $a \oplus r$입니다.
그러면 $[(a \oplus r) \ and \ b] \oplus [r \ and \ b]$에서 $(a \oplus r) \ and \ b$는 Evaluator가 하나의 값을 아는 and 연산이고 $r \ and \ b$는 Garbler가 하나의 값을 아는 and 연산입니다.
E-1. Garbler half-gate
먼저 Garbler가 하나의 값을 아는 and 연산을 생각해봅시다. Garbler가 알고 있는 하나의 값 $a$가 0이라면 출력은 반드시 0이어야 하고, 1이라면 출력은 $b$가 그대로 나옵니다. 즉 Garbler가 알고 있는 값이 0인지 1인지에 따라 아래와 같이 테이블을 만들면 됩니다.
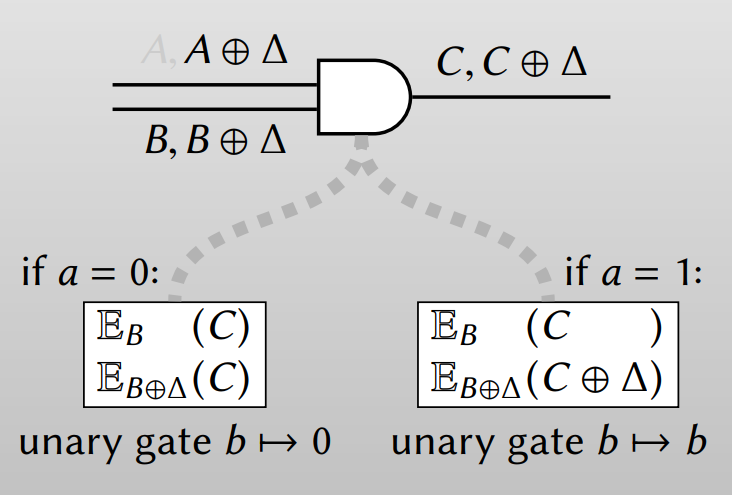
이를 하나의 테이블로 표현하면 아래와 같습니다.
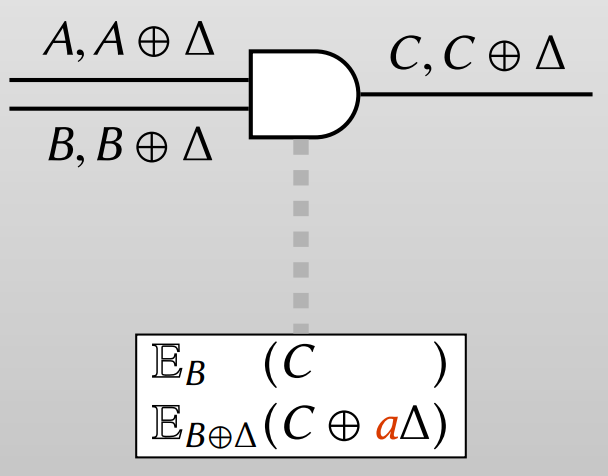
마지막으로 C. Row Reduction에서 언급한 테크닉을 그대로 사용하면 하나의 암호문 만으로 Garbler half-gate를 계산할 수 있습니다.
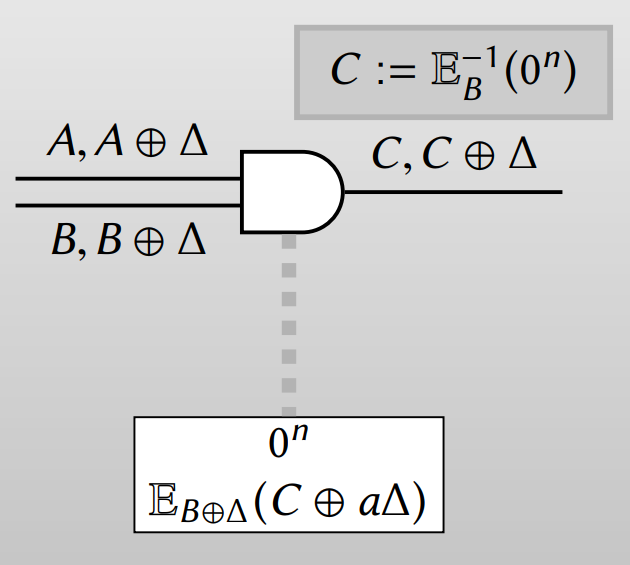
E-2. Evaluator half-gate
Evaluator가 하나의 값을 아는 and 연산을 생각해봅시다. Evaluator가 알고 있는 하나의 값 $b$가 0이라면 출력은 반드시 0이어야 하고, 1이라면 출력은 $a$가 그대로 나옵니다. Garbler는 $b$가 0인지 1인지 모르니 테이블을 하나지만 Evaluator가 자신이 들고 있는 값에 따라 값을 어떻게 연산할지 정합니다. 아래와 같이 테이블을 정해둔 상황을 생각해봅시다.
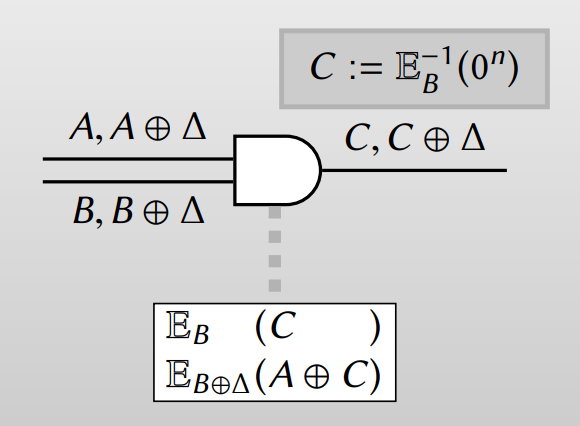
Evaluator가 0을 들고 있었다면 바로 복호화를 통해 출력 wire에 대응되는 값인 $C$를 알 수 있습니다. 1을 들고 있었다면 $A \oplus C$를 알 수 있는데, 이를 Garbler 쪽의 wire 값과 XOR을 취해 출력 wire의 값을 알 수 있습니다.
만약 Garbler 쪽에서의 값이 0이어서 $A$를 들고 있었다면 $A \oplus (A \oplus C) = C$를 통해 $C$를 얻고 1이어서 $A \oplus \Delta$를 들고 있었다면 $(A \oplus \Delta) \oplus (A \oplus C) = C \oplus \Delta$를 얻습니다.
여기서도 마찬가지로 Row Reduction을 통해 하나의 암호문만을 필요로 합니다.
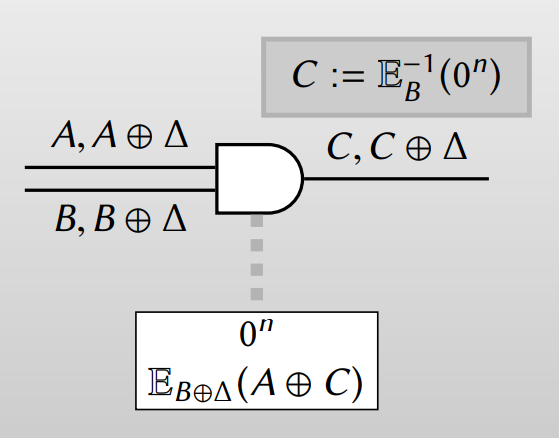
최종적으로 Generator half-gate로 얻은 결과와 Evaluator half-gate로 얻은 결과를 XOR하면 AND를 수행할 수 있습니다. 각 AND gate에서는 2개의 암호문을 필요로 합니다.
4. Conclusion
이번 글을 통해 Multi-Party Computation과 Garbled Circuit의 발전 흐름을 알아보았습니다. 이 방법을 이용해 Secure Multi-Party Computation을 수행하는 프로그램을 만들 수 있고, 실제로 Garbled Curcuit을 이용해서 일반적인 C 프로그램을 secure computation이 가능하도록 해주는 Obliv-C라는 컴파일러가 있습니다. 특히 요즘 들어 Privacy Preserving에 대한 수요가 올라가고 있는 상황에서 Garbled Circuit은 공부해볼 가치가 있다고 생각합니다.
다음 글에서는 실제 구현상의 이슈와 관련된 provable security에 대해 알아보고자 합니다.