LSM Tree
안녕하세요?
오늘은 데이터베이스 시스템에서, key-value 형태의 데이터를 저장할 때 좋은 성능을 내는 LSM Tree(Log-Structured Merge Tree)에 대해 알아보겠습니다.
보통 key-value 형태의 데이터를 저장할 때는 B-Tree를 많이 사용합니다. 하지만 만약 저장되는 매체가 disk라면, B-Tree는 많은 random access를 발생시켜 저조한 성능을 내게 됩니다.
하지만 이 때 LSM Tree를 사용하면, write를 할 때 append only 방식으로 저장을 하기때문에, write를 sequential하게 처리하여 성능을 향상시킬 수 있습니다.
LSM Tree의 기본 구조
LSM Tree는 1996년 Patrick O’Neil의 논문 The Log-Structured Merge-Tree (LSM-Tree)에서 처음 발표되었습니다.
시기적으로, 당시에는 메모리가 굉장히 비용이 비싼 자원이었기 때문에, 현재 많이 사용되는 LSM Tree의 구조와는 다소 차이가 있습니다. 첫 논문에서 제안된 구조는 메모리에 존재하는 C0 레벨과 디스크에 존재하는 C1 두 개의 레벨만이 존재하며, 각 레벨은 각각 Compact B Tree라는 구조를 유지하였지만 현재 많이 사용되는 LSM Tree의 경우에는 훨씬 더 많은 레벨이 존재하고, 구조 또한 약간 다릅니다.
현재 사용되는 LSM Tree도 사용되는 곳마다 각각 차이점이 존재합니다. 이 글에서는 Monkey: Optimal Navigable Key-Value Store라는 논문에서 언급한 형태를 기본으로 하여 간단히 구조를 알아보겠습니다.
먼저, LSM Tree에는 총 0~L까지의 레벨이 존재합니다. 0번 레벨은 메모리에 위치하고, 1~L번 레벨은 디스크에 존재합니다. 0번 레벨에 위치한 buffer는 데이터가 저장되며, buffer의 크기가 가득 차면 그 때부터 한 칸씩 아래 레벨로 flush됩니다.
Buffer에 key와 value를 모두 저장할 수도 있고, value는 다른 곳에 저장하고 key와 value에 대한 포인터만 저장하는 방법도 사용할 수 있습니다. (key-value separation)
또, Size ratio T가 존재하여 각 레벨별로 사이즈가 T배씩 커집니다. 만약 T = 3이고, 0번 레벨에 최대 2개의 key-value pair가 존재할 수 있다면, 1번 레벨에는 최대 6개, 2번 레벨에는 최대 18개, …의 key-value pair들이 존재할 수 있습니다.
각각의 레벨에는 run이라 불리는 하나의 레벨에 여러 개의 run을 유지할 수도 있고, 하나의 run만을 유지할 수도 있습니다. 여러 개의 run을 유지하는 경우 Tiered LSM Tree, 단 하나의 run만을 유지하는 경우 Leveled LSM Tree라 하는데 여기서는 Leveled LSM Tree만을 살펴보도록 하겠습니다.
각 run 내부에서는 key들이 정렬된 상태로 유지되어 있습니다.
한 레벨의 run이 가득 찰 때마다, 해당 데이터를 아래의 레벨로 내려주는데, 이 때 run 내부에서 정렬된 상태를 유지하여야 하기 때문에 원래 아래 레벨에서 가지고 있던 데이터들과 합쳐 다시 한 번 정렬을 하게 됩니다. 이 과정에서 merge sort 방식이 들어가기 때문에, LSM Tree라는 이름이 붙게 되었습니다.
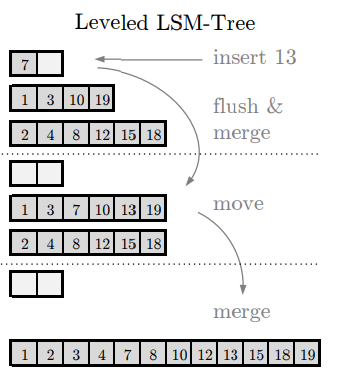
Fig 1. LSM Tree의 insert (출처: Monkey 논문)
위 Fig 1은 LSM Tree 작동의 예시를 나타냅니다. 13이라는 key가 추가로 삽입되면, level 0이 가득차게 되므로 해당 데이터들을 한 칸 아래쪽으로 보내며 정렬합니다. 이 떄, level 1의 run도 가득차게 되므로 이를 다시 level 2로 내려보낸 뒤 정렬합니다. 최종적으로 가장 아래쪽의 형태를 띠게 됩니다.
이제 key를 이용하여 저장된 데이터를 찾는 방법에 대해 알아보겠습니다. 레벨이 높아질수록 run의 크기가 커지기 때문에, 하나의 run의 disk 내의 여러 page에 거쳐있는 경우가 발생하게 됩니다.
따라서, 먼저 key가 주어졌을 때 이 key가 어떤 범위에 속해있는지(즉, 어떤 page에 들어있을 가능성이 있는지)를 판단할 수 있어야 합니다. 이를 위해 메모리에 fence pointer를 유지하여 각 page의 위치와, 해당 page에 저장된 key의 min/max값을 저장합니다. 이제 하나의 key에 대한 lookup 요청이 왔을 때, fence pointer를 binary search하여 page를 찾아낸 뒤, 해당 page를 읽어 실제로 key가 들어있는지를 확인하면 됩니다.
추가적으로, 각 레벨에 bloom filter를 유지하기도 합니다.
bloom filter는 원소가 집합에 속하는지 여부를 확률적으로 알아낼 수 있는 자료구조로, 자세한 내용은 Bloom filter에 관한 글 등을 참고하실 수 있습니다. Bloom filter를 통해 데이터가 없다고 판단되었을 경우, 실제로도 찾으려는 데이터가 존재하지 않는다는 것을 보장할 수 있기 때문에 추가적인 extra I/O를 줄일 수 있습니다.
다만, 실제로 찾으려는 데이터가 존재하지 않음에도 bloom filter에서는 데이터가 없다고 판단하지 않는, False positive가 발생할 수도 있습니다.
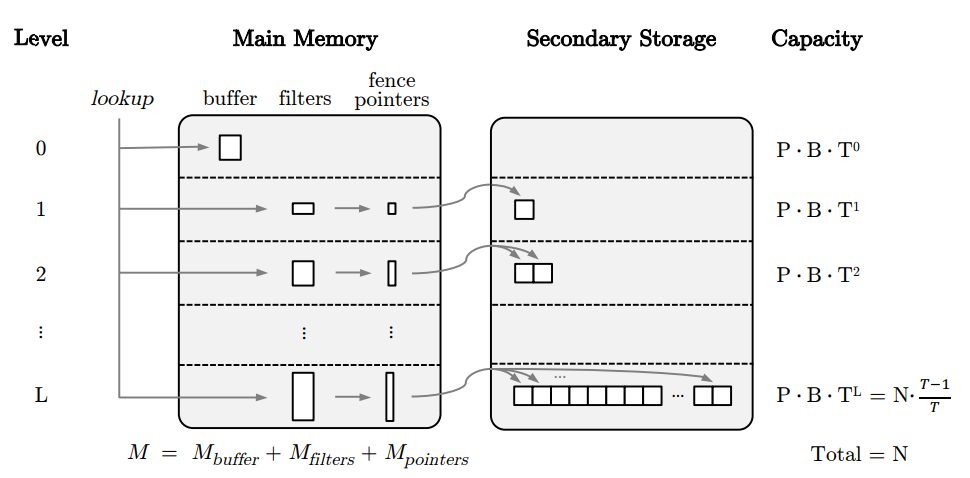
Fig 2. LSM Tree key-value store (출처: Monkey 논문)
최종적으로, LSM Tree를 이용한 key-value 저장은 다음과 같은 형태를 띠게 됩니다.
LSM Tree의 시간 복잡도
먼저 lookup에 대한 시간 복잡도를 확인해보겠습니다. 하나의 lookup에 대해, worst한 경우는 실제 key가 저장되어있지 않은데 lookup을 하게 되는 경우입니다. 이 경우, 모든 레벨을 다 찾아보아야 하므로 I/O는 최대 $O(L)$번 발생하게 됩니다. bloom filter를 사용한다면 이를 $O(Le^{\frac{-M_{filter}}{N}})$회로 감소시킬 수 있습니다. 이 때 뒤의 지수 부분은 bloom filter에서 False positive가 발생할 확률입니다.
다음은 write 연산입니다. Write의 경우 맨 처음에 메모리에 있는 buffer에 쓰이기 때문에 추가적인 I/O를 발생시키지 않지만, 이후 buffer가 가득 차며 한 레벨씩 아래로 내려갈 때 계속해서 I/O가 발생하기 때문에, 해당 I/O를 계산해야 합니다.
이에 대한 평균적인 update 비용을 Amortized하게 계산해볼 수 있습니다. 결국 모든 key들은 가장 아래의 레벨로 내려가게 되는데, 이 때까지 해당 key에 의한 update가 몇 번 발생했는지를 따져보면 쉽게 유추할 수 있습니다.
먼저 한 레벨이 내려갈 때마다 해당 key를 write를 해주어야 한다는 것을 알 수 있습니다.
둘째로 해당 level에 존재할 때, 윗 레벨이 가득 차서 compaction이 발생하면 정렬된 상태를 유지하기 위해 merge를 해준 뒤 데이터를 다시 저장해주어야 하기 때문에 추가적인 I/O가 발생합니다. 각 레벨별로 크기는 T배 차이가 나므로, 한 레벨이 존재할 때 compaction은 최대 T번 발생하게 됩니다.
따라서 최종적으로, update 비용은 $O(\frac{TL}{B})$임을 알 수 있습니다. 여기서 B는 하나의 단위에 저장되는 key의 개수입니다.
보통 B는 T와 L에 비해 굉장히 큰 값이므로, write의 경우 그리 큰 write amplification을 발생하지 않는 것을 알 수 있습니다. 하지만, read의 경우 성능이 크게 저하될 수 있습니다.
Reference
다음은 글을 작성할 때 참고한 논문입니다.