March 19, 2021 12:43

개요

그래프는 일상생활 뿐만 아니라 대부분의 과학 분야에서 ‘추상화’를 위해 사용하는 아주 강력한 자료 구조이다. 그래프의 중요한 성질로 여러 가지가 있으며, 이 글은 그 중에서 특히 절점과 절선에 대하여 다룬다.

무방향 그래프에서 각 간선을 끊었을 때, 그래프의 절점의 개수를 효율적으로 세는 알고리즘에 대하여 알아보고자 한다.

즉, 이 알고리즘은 다음과 같은 일상생활 속 문제를 해결할 수 있게 도와준다:

사내 서버망에서 어떤 회선이 끊어졌다고(불능이 되었다고) 하자.

여기서, 추가적으로 어떤 서버가 고장나야 서버망이 끊기게 되는가.

즉, 어떤 ‘중요한’ 서버를 지켜야, 모든 서버가 연결된 상태로 존재할 수 있는가.

본문에서는 다음의 내용을 부가적인 설명 없이 서술한다. 각 항목에 대하여, 자세하게 서술한 좋은 글을 링크해두었다.

• 절점 (Separating Vertex), 절선 (Bridge), BCC
• 최소 공통 조상 (LCA, Lowest Common Ancestor)

문제 제시

$N$개의 정점과 $M$개의 간선으로 이루어진 무방향 연결 그래프 $G(V, E)$가 주어진다.

각 간선 $e \in E$에 대하여, 간선 $e$를 제거한 그래프 $G(V, E \setminus \{ e \})$의 절점의 개수를 모두 구해보자.

문제 접근

표기의 편의를 위하여, 그래프 $G$의 절점의 집합을 $C(G)$라고 나타내자.

우리의 목표는 모든 $e \in E$에 대하여, $\left\lvert C\left( G(V, E \setminus \{ e \}) \right) \right\rvert$를 효율적으로 구하는 것이다.

중요한 접근

절점이란, 그래프에서 그 정점을 제거하면 연결성이 사라지는 그러한 정점을 의미한다. 그렇다면, ‘이미 절점이었던 정점’이 간선 제거 이후에 ‘절점이 아니게 되는’ 경우가 존재할까? 절점의 입장에서 간선의 제거는 ‘그래프가 끊기도록 도와주는’ 역할을 할 것이므로, 간선을 끊었다고 절점이 사라지는 현상은 발생하지 않을 것 같다.

아래의 절점 보존 정리는 우리의 생각이 맞다는 것을 보여준다.

정리 (절점 보존 정리)

모든 $e \in E$에 대하여, $C\left( G(V, E) \right) \subset C\left( G(V, E \setminus \{ e \}) \right)$가 성립한다.

즉, 간선을 제거하였다고 절점이 사라지는 일은 발생하지 않는다.

증명

귀류법을 이용하자.

만일, 어떤 $e \in E$과 $v \in V$에 대하여, $v \in C\left( G(V, E) \right)$이고 $v \not\in C\left( G(V, E \setminus \{ e \}) \right)$라고 하자. 즉, $v$는 이미 절점이었는데, 간선 $e$를 제거함으로써 절점이 아니게 되었다고 가정하자.

$G(V, E \setminus \{ e \})$에서 $v$가 절점이 아니므로, 정의에 의하여, $v$를 제거한 그래프 $G(V \setminus \{ v \}, E \setminus \{ e \})$는 연결 그래프이다.

$v$와 $e$를 제거한 그래프가 연결 그래프이므로, $G(V \setminus \{ v \}, E \setminus \{ e \})$에서 신장 부분 트리 $T’$를 생성할 수 있다.

트리 $T’$는 간선 $e$를 포함하지 않으므로, $T’$는 $G(V \setminus \{ v \}, E)$의 신장 부분 트리이기도 하다.

즉, 그래프 $G(V, E)$에서 정점 $v$를 제거하여도 연결성이 유지되므로, $v$는 $G(V, E)$에서 절점이 아니다.

모순이 발생하였고, 따라서 증명이 끝난다.

절점 보존 정리에 따라서, 우리는 각 간선 $e$를 제거하였을 때, 어떤 정점이 ‘새롭게 절점이 되는지’만을 알아내면 된다. 이렇게, ‘간선 $e$를 제거하였을 때 새롭게 절점이 되는 정점의 집합’을 $R(e)$라고 하자. 다음 따름정리에 의하여, 우리는 $R(e)$만 계산해도 된다는 정당성을 얻을 수 있다.

따름정리

모든 $e \in E$에 대하여, $C\left( G(V, E \setminus \{ e \}) \right) = C\left( G(V, E) \right) \cup R(e)$가 성립한다.

또한, 두 집합 $C\left( G(V, E) \right)$과 $R(e)$는 서로소이다.

알려진 정리 (절점·절선 알고리즘)

그래프 $G(V, E)$가 주어졌을 때, 집합 $C\left( G(V, E) \right)$는 단 한 번의 DFS를 통하여, $O \left( \left\lvert V \right\rvert + \left\lvert E \right\rvert \right)$의 시간 복잡도로 계산할 수 있다.

이제, 집합 $R(e)$의 특징을 관찰하자. 이 집합에 속하는 정점은 간선 $e$와 ‘관련 없는’ 곳에 위치하지는 않을 것이다. 다음 사이클 정리는 집합 $R(e)$에 대한 아주 핵심적인 특징을 말해준다.

정리 (사이클 정리)

그래프 $G(V, E)$에서 간선 $e \in E$를 포함하는 단순 사이클 $C = \{ v_1, v_2, \cdots, v_k \}$를 생각하자. 집합 $R(e)$의 모든 정점은 사이클 $C$ 위에 존재한다. 즉, $R(e) \subset C$이다.

증명

귀류법을 이용하자.

간선 $e \in E$와 단순 사이클 $C = \{ v_1, v_2, \cdots, v_k \}$를 고정하자. 여기서, 집합 $R(e)$에는 포함되나, 사이클 $C$ 위에 존재하지 않는 정점 $v \in V$가 존재한다고 하자. 즉, $v \in R(e)$, $v \not\in C$이다.

$v \in R(e)$이므로, 정점 $v$와 간선 $e$를 제거한 그래프는 연결되어 있지 않다. 다시 말하면, $v$가 아닌 두 정점 $x$, $y$가 존재하여, 그래프 $G(V, E)$에서 그 둘을 잇는 모든 경로는 무조건 정점 $v$와 간선 $e$를 모두 지나야 한다. 왜냐하면, 정점 $v$는 원본 그래프 $G(V, E)$에서는 절점이 아니었기 때문이다.

하지만, 그림 1과 같이, 간선 $e$를 지나는 경로는 항상, 간선 $e$를 지나지 않도록 변형할 수 있다. 간선 $e$를 포함하는 단순 사이클 $C$가 존재하기 때문에, 간선 $e$를 지나지 않도록 ‘반대 방향으로 단순 사이클 $C$를 따라 돌아가면’ 된다.

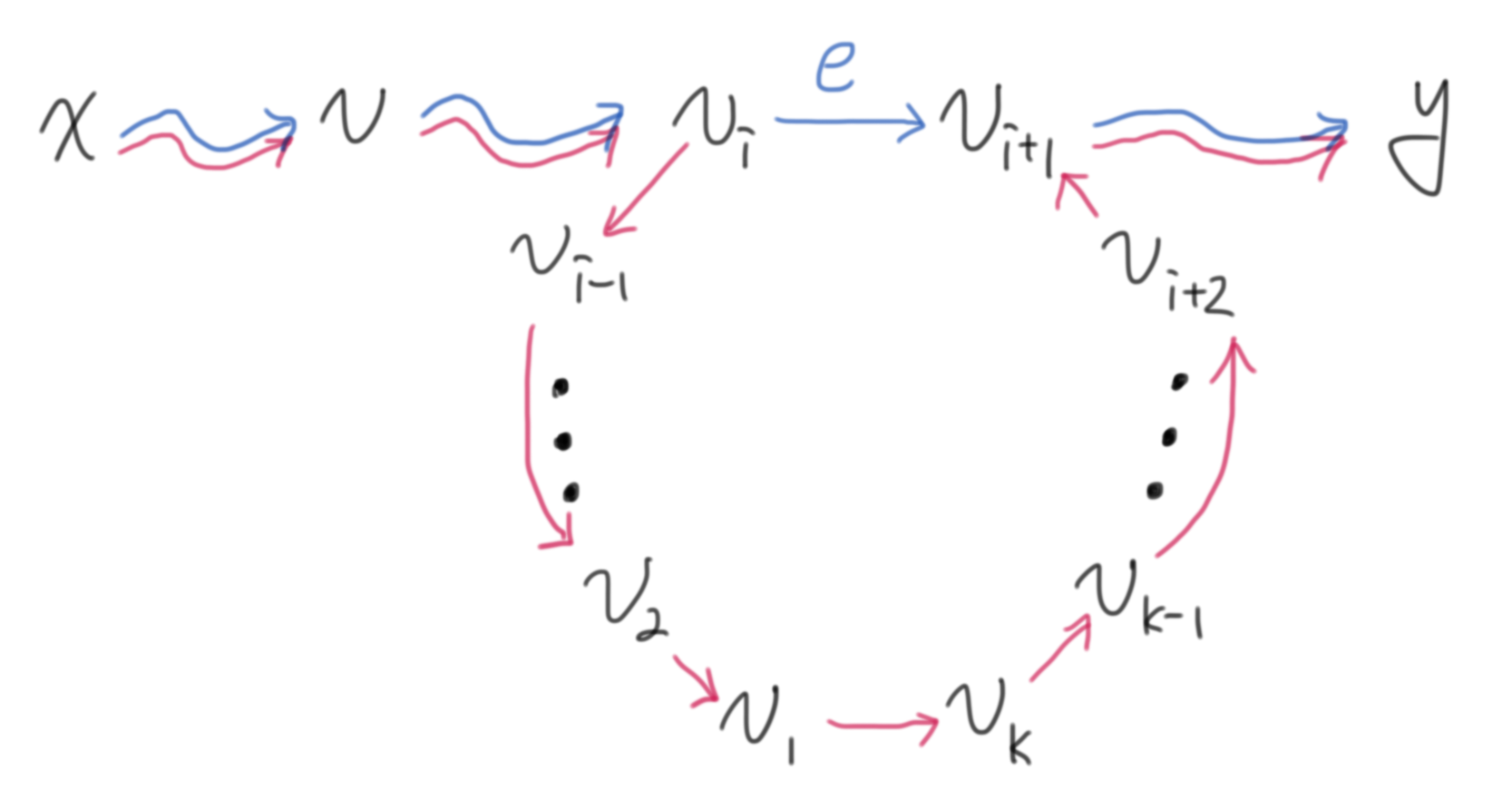
그림 1: 간선 $e$를 지나지 않는 단순 경로

정점 $x$에서 $y$로 도달하기 위하여, 파란 경로와 같이 정점 $v$와 간선 $e$를 사용하여야 한다면, 빨간 경로와 같이 간선 $e$를 지나지 않도록 항상 변형할 수 있다.

따라서, 모순에 도달하였고, 증명이 끝난다.

정리 (이웃 정리)

모든 간선 $e = (u, v) \in E$에 대하여, 집합 $R(e)$는 간선 $e$가 잇는 두 정점을 모두 포함하지 않는다. 즉, $u \not\in R(e)$, $v \not\in R(e)$이다.

증명

귀류법을 이용하자.

어떤 간선 $e = (u, v) \in E$에 대하여, 일반성을 잃지 않고, $u \in R(e)$라고 가정하자.

$u \in R(e)$이므로, 정점 $u$와 간선 $e$를 모두 제거하면, 그래프는 끊기게 된다.

그러나, 정점 $u$를 제거하면 필연적으로 간선 $e$도 같이 제거된다. 정점 $u$에 간선 $e$가 붙어있기 때문이다.

따라서, 그래프 $G(V, E)$에서 정점 $u$는 이미 절점이다. 이는 $R(e)$의 정의와 모순이다.

모순이 발생하였고, 고로 증명이 끝난다.

알려진 정리 (절선의 다른 정의)

간선 $e \in E$에 대하여, 다음 두 명제는 서로 동치이다.

• 간선 $e$를 포함하는 단순 사이클 $C$가 존재하지 않는다.
• 간선 $e$는 절선이다.

따름정리

절선 $e = (u, v)$에 대하여, $R(e) = V \setminus \left( C\left( G(V, E) \right) \cup \{ u, v \} \right)$이다.

절선을 제거하면, 이미 그래프가 끊겨버리므로, 모든 정점이 절점이 된다는 의미이다.

정리 (BCC 독립 정리)

절선이 아닌 간선 $e$가 어떤 BCC에 포함된다면, 집합 $R(e)$에 속하는 모든 정점도 동일한 BCC에 속한다.

증명

BCC의 정의와, 사이클 정리에 의하여 성립한다.

상기한 따름정리는, 우리가 절선이 아닌 간선 $e$에 대해서만 $R(e)$를 구해도 된다는 사실을 알려준다. 또한, BCC 독립 정리는 그래프를 BCC들로 분리한 다음, 각 BCC에 대하여 독립적으로 처리해도 됨을 말해준다.

이제부터, 그래프 $G(V, E)$가 하나의 BCC라고 가정하자. 일반적인 그래프 $G(V, E)$의 모든 BCC를 구한 후, 각각에 대하여 처리한다고 생각해도 된다. 이 과정은 다음 BCC 분할 정리에 의하여, 선형에 처리할 수 있다.

알려진 정리 (BCC 분할)

그래프 $G(V, E)$의 모든 BCC를 $G_1 \left( V_1, E_1 \right), G_2 \left( V_2, E_2 \right), \cdots, G_K \left( V_K, E_K \right)$라고 하자. 여기서, 다음이 성립한다:

• $\displaystyle \sum _{i = 1}^{K} \left\lvert V _i \right\rvert = \left\lvert V _1 \right\rvert + \left\lvert V _2 \right\rvert + \cdots + \left\lvert V _K \right\rvert \le 2 \left\lvert V \right\rvert$
• $\displaystyle \sum _{i = 1}^{K} \left\lvert E _i \right\rvert = \left\lvert E _1 \right\rvert + \left\lvert E _2 \right\rvert + \cdots + \left\lvert E _K \right\rvert \le \left\lvert E \right\rvert$

또한, 모든 BCC를 알아내는 작업은 $O \left( \left\lvert V \right\rvert + \left\lvert E \right\rvert \right)$의 시간 복잡도로 해결할 수 있다.

BCC 그래프에서 문제 접근

BCC 그래프 $G(V, E)$에서 루트 정점 $r \in V$부터 DFS를 시행하여, DFS 트리 $T$를 생성하자. $R(e)$를 계산하기 위한 해결 전략은 다음과 같다:

• DFS 트리 $T$에 속하지 않는 간선 $e$에 대하여, $R(e)$를 계산
• DFS 트리 $T$에 속하는 간선 $e$에 대하여, $R(e)$를 계산
  • DFS 트리 $T$에서, 간선 $e$보다 위에 존재하는 $v \in R(e)$를 모두 알아내기
  • DFS 트리 $T$에서, 간선 $e$보다 아래에 존재하는 $v \in R(e)$를 모두 알아내기

사이클 정리에 의해, ‘위’, ‘아래’라는 표현을 사용할 수 있다는 점을 상기하자.

DFS 트리 $T$에 속하지 않는 간선 $e$에 대하여, $R(e)$ 계산

간선 $e$는 DFS 트리에 속하지 않으므로, Back edge이다.

다음 그림과 같이, Back edge $e = (\alpha, \beta)$를 끊었을 때 정점 $v$가 새로운 절점이 되려면,

• 정점 $v$는 두 정점 $\alpha$와 $\beta$ 사이에 위치하여야 하며
• 정점 $v$의 자식 정점을 $c(v)$라고 할 때, 부트리 $T_{c(v)}$에서 위로 올라가는 유일한 간선이 $e = (\alpha, \beta)$라야 한다.

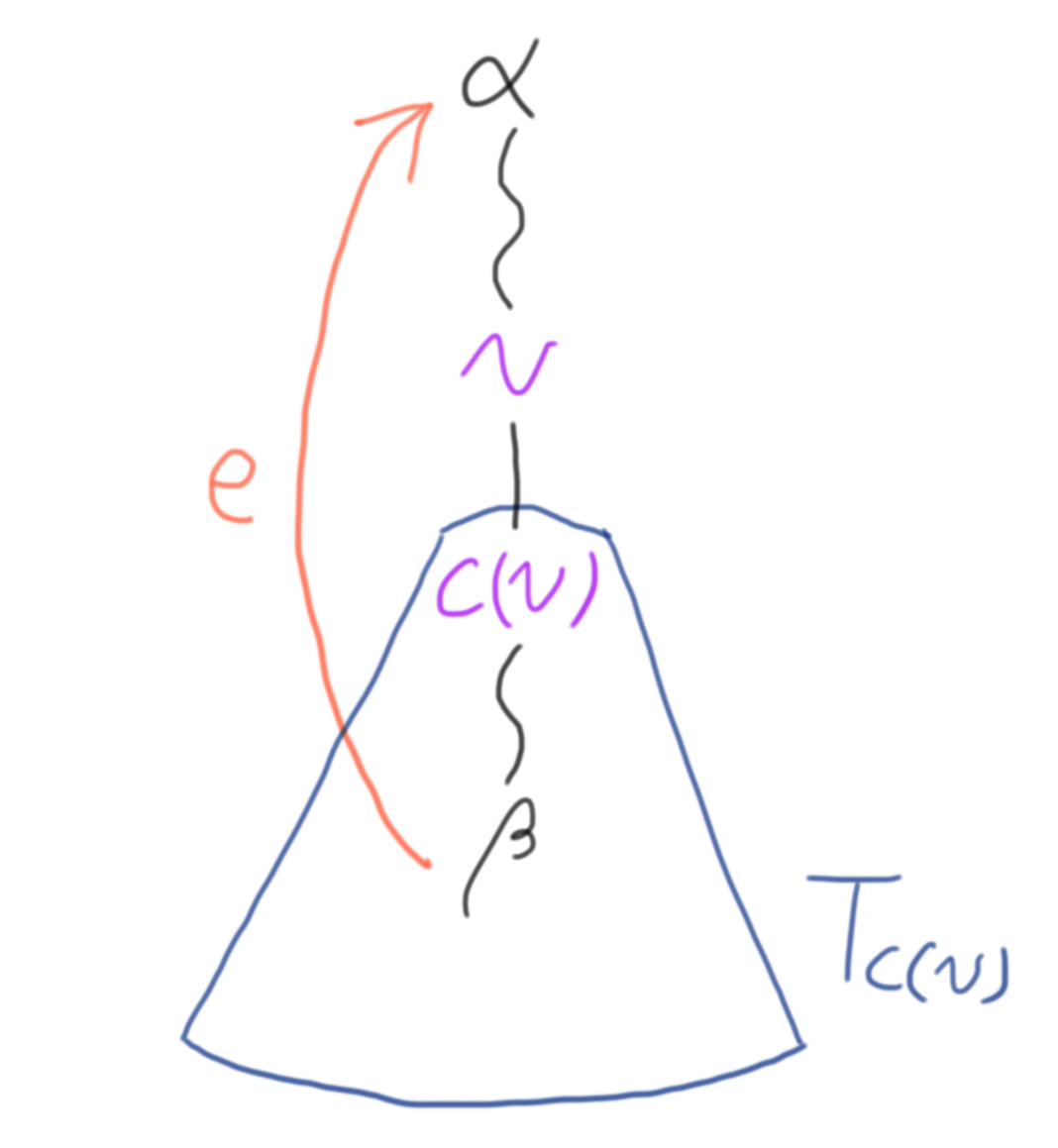
그림 2: Back edge $e$를 끊었을 때, 정점 $v$가 새로운 절점이 되는 일반적인 경우

이는 다음과 같이 부분 합의 아이디어를 이용하면, $O \left( \left\lvert V \right\rvert + \left\lvert E \right\rvert \right)$에 처리할 수 있다.

prefix_sum = [0] * N

def dfs(v):
	if 1 == len(above_edges(v)):
		prefix_sum[v] += 1
	
	for u in T[v]:
		dfs(u)
		prefix_sum[v] += prefix_sum[u]

dfs(0) # DFS from root vertex 0

for (alpha, beta) in back_edges:
	child_alpha = child(alpha)

	answer = prefix_sum[child_alpha] - prefix_sum[beta]

DFS 트리 $T$에 속하는 간선 $e$에 대하여, $R(e)$ 계산

간선 $e$가 DFS 트리에 속하므로, 이는 Tree edge이다. 편의를 위해, $e = (v, p(v))$라고 나타내자. 여기서, $p(v)$는 정점 $v$의 유일한 부모 정점을 의미한다.

간선 $e$보다 위에 존재하는 $v \in R(e)$ 찾기

Tree edge $e = (v, p(v))$를 끊었을 때, 정점 $p(v)$보다 위에 있는 정점 $u$가 새로운 절점이 되었다고 하자. 이것이 가능하려면, 그림 3과 같이, 간선 $e$를 끊은 이후에, 두 부트리 $T _v$와 $T _{c(u)} \setminus T _v$는 연결성을 잃어버려야 한다.

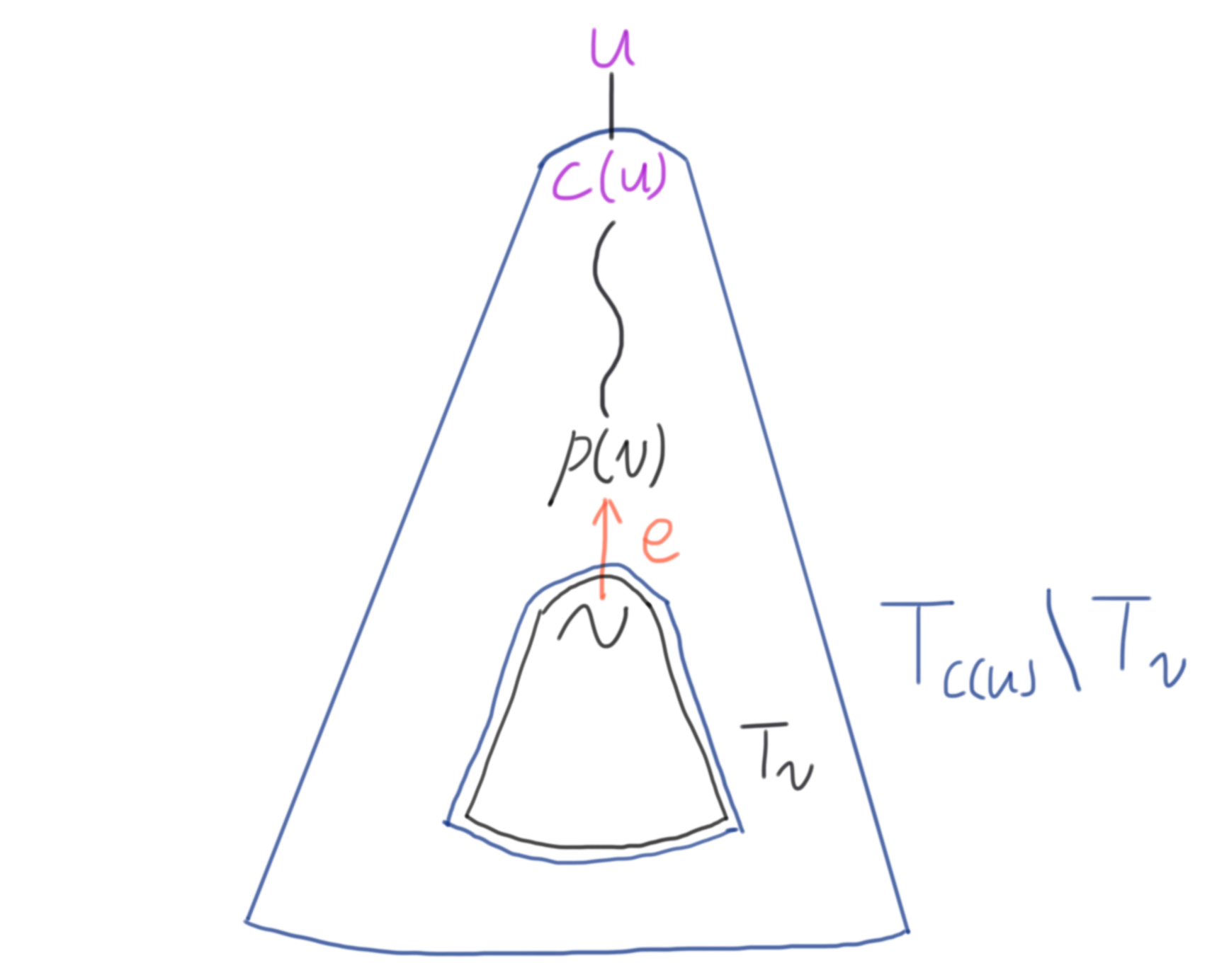
그림 3: Tree edge $e$를 끊었을 때, 위에 존재하는 정점 $u$가 새로운 절점이 되는 경우

이는 일반적으로, 부트리 $T_v$에서 위로 올라가는 모든 간선이 $(u, *)$와 같은 형태일 때 일어난다. 이 또한 간단하게 선형 시간에 해결할 수 있다.

for v in V:
	edges = up_edges(v) # all up-edges from T_v

	# get all upper vertices from edges
	up_vertices = map(lambda (a, b): a, edges)

	min_u = min(up_vertices)
	max_u = max(up_vertices)

	if min_u == max_u:
		u = min_u

		# u is an answer vertex for a tree edge (v, p(v))

간선 $e$보다 아래에 존재하는 $v \in R(e)$ 찾기

Tree edge $e = (v, p(v))$를 끊었을 때, 정점 $v$보다 아래에 존재하는 정점 $t$가 새로운 정점이 된다는 것은, 일반적인 경우, 두 부트리 $T_v \setminus T_t$와 $T_\gamma \setminus T_v$가 끊어진다는 것과 동치이다. 여기서, $\gamma$는 DFS Tree $T$의 루트 정점이다.

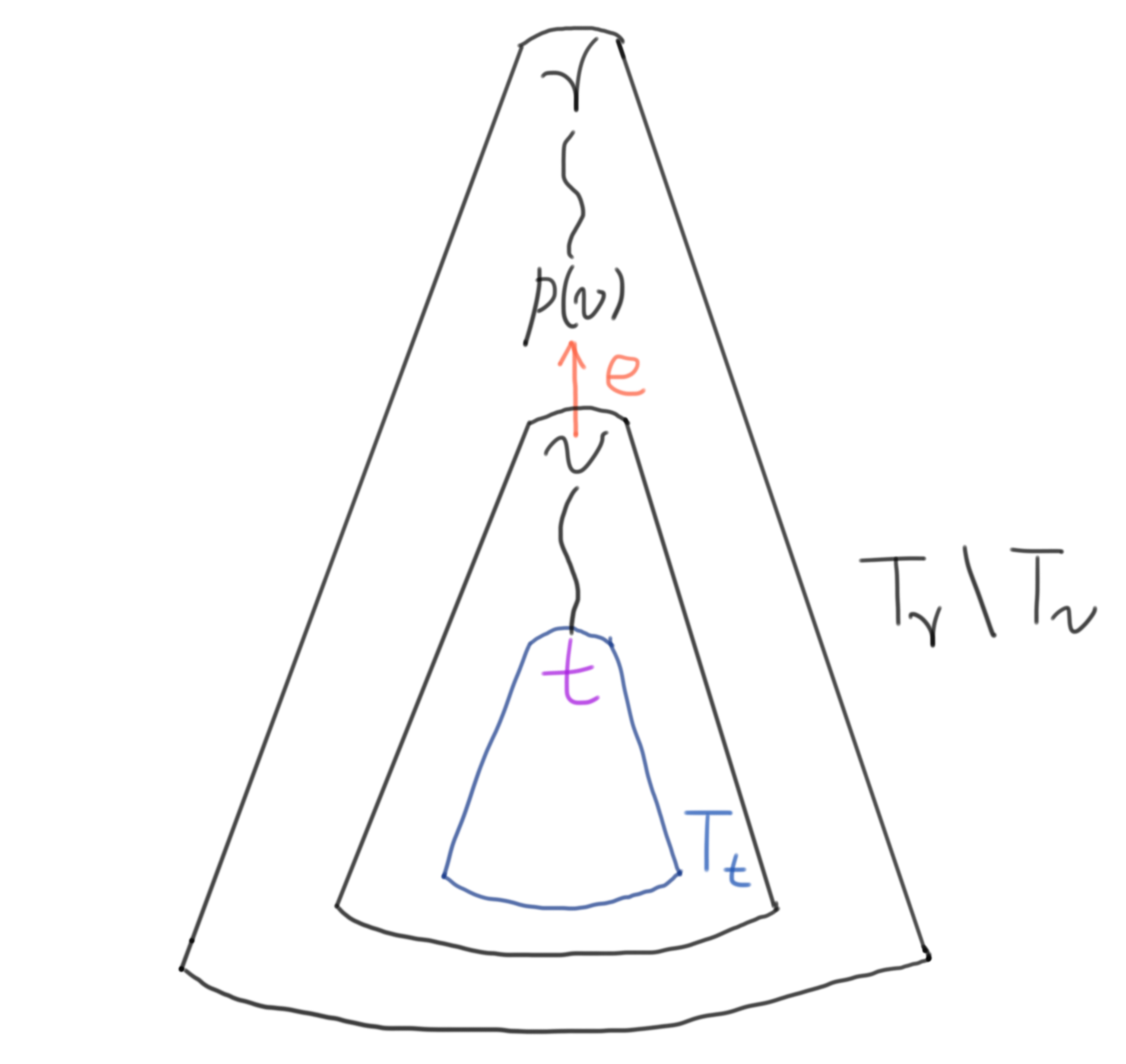
그림 4: Tree edge $e$를 끊었을 때, 아래에 존재하는 정점 $t$가 새로운 절점이 되는 일반적인 경우

정점 $t$로 가능한 모든 정점은, 일반적으로 DFS Tree $T$에서 경로 $\displaystyle \left[ t _\text{min}, v \right)$를 이루게 된다. 다음 코드는, 최소 공통 조상의 아이디어를 이용하여, 그 경로의 시작 정점 $t _\text{min}$을 $O \left( ( \left\lvert V \right\rvert + \left\lvert E \right\rvert ) \lg \left\lvert V \right\rvert \right)$에 계산한다.

for v in V:
	edges = up_edges(v) # all up-edges from T_v

	# get all lower vertices from edges
	down_vertices = map(lambda (a, b): b, edges)

	# Note that edges are non-empty!
	assert(len(down_vertices) > 0)
	
	# initial value for t_min
	t_min = down_vertices[0]

	# compute lca(down_vertices[0], down_vertices[1], ...)
	for down in down_vertices:
		t_min = lca(t_min, down)
	
	# now, t_min is a lca for all down_vertices
	# Done!

이제, 모든 케이스를 해결하였다! 일반적이지 않은, 특수한 케이스 처리가 필요하나, 위에서 서술한 방법과 아주 유사하게 해결할 수 있다. 따라서, 전체 문제를 $O \left( \left( \left\lvert V \right\rvert + \left\lvert E \right\rvert \right) \lg \left\lvert V \right\rvert \right)$에 해결할 수 있다.

결론

무방향 연결 그래프 $G(V, E)$가 주어졌을 때, 각 간선 $e \in E$에 대하여, 간선 $e$를 제거한 그래프 $G(V, E \setminus { e })$의 절점의 개수를 모두 구하는 알고리즘을 구상하였고, $O \left( \left( \left\lvert V \right\rvert + \left\lvert E \right\rvert \right) \lg \left\lvert V \right\rvert \right)$의 시간 복잡도로 효율적으로 해결할 수 있음을 알아내었다.

Disjoint Set과 Tarjan’s Offline Lowest Common Ancestors Algorithm, 그리고 약간의 창의적인 아이디어를 추가하면, 시간 복잡도를 $O \left( \left\lvert V \right\rvert \alpha \left( \left\lvert V \right\rvert \right) + \left\lvert E \right\rvert \right)$까지 개선할 수 있다. 이는 거의 선형 시간에 가까우며, 또한 이 문제를 해결하는 알고리즘의 최소 하계 $O \left( \left\lvert V \right\rvert + \left\lvert E \right\rvert \right)$와 거의 비슷하다.

이 문제는 곧 BOJ에 업로드될 예정이다. 직접 코딩한 소스 코드의 정당성을 BOJ에서 확인할 수 있다.