Minimum Cuts in Near-Linear Time
Introduction
Weighted graph $G$에 대해, $G$의 min-cut 혹은 edge connectivity 는 $G$의 connected component가 둘 이상이 되도록 하기 위해 제거해야 하는 가중치 합으로 정의됩니다. 이름 그대로 네트워크를 단절시키기 위해 필요한 최소 비용으로, 수많은 파생과 응용이 가능합니다.
이 글에서는 $n$개의 정점, $m$개의 간선을 가진 weighted graph $G$의 min-cut을 near-linear time ($\tilde{O}(m)$)에 구하는 최초의 방법인 D. R. Karger의 Minimum Cuts in Near-Linear Time을 리뷰합니다.
Definition
그래프 $G$는 non-negative weighted graph로 가정합니다. 즉, weight는 음 아닌 실수 값을 가질 수 있습니다. 음수 간선을 가진 그래프의 weighted min-cut은 NP-hard problem입니다.
그래프 $G$의 cut은 $V(G)$의 분할 $(A, \overline{A})$에 의해 정의되며, 이 cut의 value는 $A$와 그 여집합 $\overline{A}$ 사이를 잇는 간선들의 weight 합으로 정의합니다. 문맥에 따라, 그러한 간선들의 집합을 cut으로 identify하기도 합니다. min-cut은 cut들 중 가장 작은 value를 갖는 cut (혹은 그 value 자체)을 말합니다.
Min-Cut의 정의로부터, weight가 실수인 경우는 유리수인 경우의 극한으로 생각할 수 있습니다. 유리수인 경우는 적당한 정수를 곱해서 정수 weight로 바꿀 수 있으니, 결과적으로 $G$의 weight는 양의 정수로 가정하기로 합니다. 이 경우, 가중치 $w$인 간선을 $w$개의 multi-edge로 생각할 수 있다는 강점이 있습니다.
Karger의 알고리즘은 Min-Cut을 높은 확률로 구해주는 Monte-Carlo algorithm입니다. 높은 확률이란, 구한 cut이 Min-Cut이 아닐 확률이 어떤 상수 $k > 0$에 대해서 $O(n^{-k})$ 정도라는 의미입니다. Monte-Carlo algorithm이란, 이 알고리즘은 $\tilde{O}(m)$ 시간 안에 확실하게 끝나지만 값의 정확성을 보장해주지는 않는다는 의미로, 특정한 approximation ratio도 보장해주지는 않습니다.
History
Weighted graph $G$의 Min-Cut을 구하는 데는 몇 가지 전혀 다른 접근법이 있었습니다. 해당 내용은 koosaga님의 글에도 친절하게 설명되어 있으며, 동일하게 Gawrychowski (2019)의 요약을 바탕으로 작성했습니다.
Maximum Flow
Minimum Cut에 의해 분리되는 두 정점 $s, t$가 반드시 존재할 테니, 단순하게 모든 $s, t$에 대해 $s - t$ minimum cut을 구하는 방법을 생각할 수 있습니다. Maxflow-Mincut theorem에 의해 $s - t$ min cut은 $s - t$ maxflow로 바꿔서 풀 수 있고, Weighted graph에 대해 동작하는 가장 빠른 flow algorithm (Orlin)은 $O(mn)$ 정도 시간이 걸립니다. Flow 계산을 한 번 하는 데 걸리는 시간이 $flow(m,n)$이라고 둡시다. 단순히 모든 $(s, t)$ 쌍을 고려하는 방법은 $O(n^2 flow(m,n))$의 시간이 걸립니다. Gomory-Hu Tree를 이용하면 $O(n \cdot flow(m,n))$ 시간에 해결할 수 있습니다. $flow(m, n)$은 near-linear time에 풀릴 것으로 보이나, Gomory-Hu보다 flow oracle을 적게 쓰는 방법은 알려지지 않았습니다. Hao, Orlin (1994)는 한 번의 maximum flow로 문제를 해결하는 방법을 제시했지만, 이는 flow 알고리즘 중 하나인 push-relabel algorithm의 성질에 크게 의존하는 것으로 보입니다. 이는 최근 복잡도 개선이 크게 이루어지고 있는 flow algorithm들과는 방법론적 차이가 있으며, 결국 $flow(m, n) = \tilde{O}(m)$임이 밝혀지더라도 near-linear time min-cut까지는 갈 길이 멉니다.
Edge Contraction
Minimum Cut에 포함되지 않는 간선 $e=uv$를 알아낼 수 있다고 합시다. 그렇다면 $G$의 minimum cut과, $u,v$를 한 정점으로 합친 $G / e$의 minimum cut은 동일합니다. $u, v$는 minimum cut에 의해 분리되는 두 집합에서 어차피 같은 쪽에 속해 있기 때문입니다. 이 아이디어에 기반한 알고리즘 중 Stoer-Wagner algorithm이 $O(mn)$ deterministic이고, 구현이 어렵지 않아 PS 수준에서 global min-cut을 구해야 하는 상황에서 사용할 법한 알고리즘입니다. Karger 본인 또한 동일한 아이디어에 기반하여 $O(n^2 \log^{3} n)$ 시간에 동작하는 Randomized algorithm을 창안하였습니다.
Tree Packing method and Karger’s achievements
Karger가 채택한 방법론이자, Min-Cut에 있어 가장 큰 개선을 가져온 방법론입니다.
Unweighted graph의 경우에, 크기 $c$인 min-cut이 존재한다면 $c/2$개 이상의 edge-disjoint spanning tree가 존재한다는 것이 알려져 있습니다. (Nash-Williams Theorem) 이러한 스패닝 트리들의 모임을 tree packing이라고 합니다. 이 때 min-cut에 들어가는 edge들은 정의상 전부 tree packing의 edge들에 속해야 하고, 때문에 Min-Cut과의 교집합이 많아야 $2$개인 트리 $T$가 존재한다는 사실을 알 수 있습니다.
Cut과의 교집합이 작은 트리 $T$를 찾을 수 있다면 어떤 점이 좋을까요? $G$의 두 정점 $u, v$에 대해, $u$에서 $v$로 가는 유일한 최단경로가 존재할 것입니다.
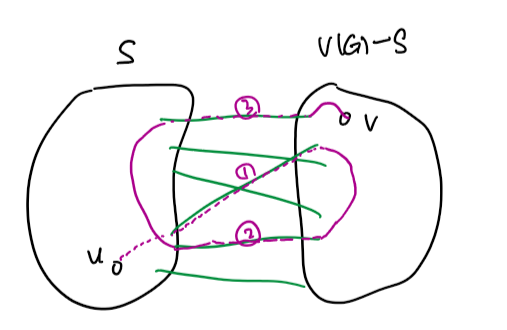
이 때 그 경로가 cut edge를 홀수 번 만나면 $u$와 $v$는 cut의 다른 편에, 짝수 번 만나면 cut의 같은 편에 위치하게 됩니다. 따라서, $T$와 Cut의 교집합에 속하는 간선들만으로 cut을 완벽하게 결정할 수 있게 됩니다.
이제 우리에게 조건을 만족하는 트리 $T$가 Cut에 대한 정보 없이 주어졌다고 합시다. 하지만 이 트리가 Min-Cut과 2개 이하의 간선에서 만난다는 사실을 알고 있다면, 트리에서 $2$개 이하의 간선을 골라 그 두 간선이 결정하는 cut의 비용을 보고, 이 중 최솟값을 구하면 그 값이 바로 min-cut이 됩니다! 이 값을 brute-force로 구하면 $O(n^2 m)$ 정도의 시간이 걸리게 되는데, 여기서 소개할 Karger의 업적 중 첫 번째가 이를 $O(m\log^{2} n)$ 시간 안에 해결한 것입니다.
결과적으로 트리 $T$에서 최대 $2$개의 간선을 골라 만들 수 있는 cut들이 중요한 대상이라는 것이 보이니 이름을 붙입시다.
- 스패닝 트리 $T$가 주어졌을 때, $T$와 간선을 최대 $k$개 공유하는 cut을 $k$-respecting cut이라고 합니다.
- Cut $C$가 주어졌을 때, $C$와 간선을 최대 $k$개 공유하는 스패닝 트리를 $k$-constraining tree라고 합니다.
이제 min-cut을 $2$-constrain하는 트리 $T$를 찾아야 하는데, 우리가 아는 건 크기가 $c / 2$보다 큰 tree packing이 있다면 그 중 하나는 있다는 것뿐입니다. 결국 $T$로 가능한 후보가 $c$에 비례하게 많아지니, 아무리 $2$-respecting cut을 빠르게 찾아도 $O(cm \log^{2} n)$이 되어 문제 해결과는 요원한 복잡도가 됩니다. 더욱이, 크기 $c$의 tree packing을 구하는 방법조차 자명하지 않습니다! Gabow (1995)는 크기 $c$의 tree packing을 찾는 $O(mc \log n)$ 알고리즘을 발표했는데, 여전히 $c$는 arbitrarily large value가 될 수 있습니다.
Karger는 이 문제에 대한 해결법으로 random sampling 기법을 고안했습니다.. Min cut $c^{\prime} = O(\log n)$이 되는 $G$의 subgraph $G^{\prime}$을 만든 뒤, $G^{\prime}$의 tree packing들 중 대부분 (with constant probability)은 Min-Cut을 $2$-constrain 하고 있다는 것을 증명함으로써, 시도할 트리 후보의 개수를 $O(\log n)$개로 줄임과 동시에 tree packing 또한 $O(n \log^{3} n)$ 시간에 무리 없이 구할 수 있도록 했습니다.
마지막으로, 기본적인 논의가 unweighted case를 가정하고 있는 만큼 weighted graph에 적용할 수 있는 방법론이 필요한데, 어렵지 않게 weighted graph에서도 같은 논의를 할 수 있습니다. Gawrychowski (2019)는 Karger의 ‘seminal work’를 아래와 같이 요약합니다:
- Tree packing의 weighted analogy를 성공적으로 이끌어낸 것.
- Random sampling과 Gabow’s algorithm을 조합하여, 상수 확률로 min-cut을 $2$-constrain하는 $O(\log n)$ 크기의 tree packing을 구한 것.
- 트리 $T$를 $2$-respect하는 cut들 중 비용이 최소인 것을 $O(m \log^{2} n)$ 시간 안에 구하는 방법을 만들어낸 것.
이를 조합하여 Karger는 weighted min-cut을 높은 확률로 구하는 $O(m\log^{3} n)$ 알고리즘을 만들어내는 데 성공합니다. 이후의 개선은 2019년에 와서야 Gawrychowski 등에 의해 이루어지는데요, $2$-respecting cut을 구하는 시간을 $T _ {2}(m,n)$이라고 두면 Karger의 algorithm은
$O(T _ {2}(m, n)\log n + m + n\log^{3} n) \text{ with } T _ {2}(m, n) = O(m\log^{2} n)$
에 동작합니다. Gawrychowski 등 후대의 업적은 $T _ {2}(m, n) = O(m \log n)$이 되도록 개선한 것으로, Karger의 framework에서 큰 틀을 빌려 쓰고 있는 셈입니다. 근 20년 간 state-of-the-art를 지키고 있는 방법론을 만들었다는 것을 통해, Karger의 접근이 얼마나 혁신적이었는지 짐작할 수 있습니다. 이제부터 그 설계도를 들여다보도록 합시다.
Weighted Tree Packing
앞서 말씀드렸듯 모든 weight가 양의 정수이기 때문에, weight $w$인 간선을 $w$개의 multi-edge로 보는 것이 자연스럽습니다. 그렇다면 다음 weighted tree packing의 정의를 받아들이기도 어렵지 않습니다.
Definition. $G$의 weighted spanning tree $T _ {1}, \cdots, T _ {k}$가 모든 간선 $e$에 대해 ($e$를 포함하는 $T _ {i}$들의 weight 합) $\le$ ($e$의 weight 합)을 만족할 때, 이 트리들을 weighted tree packing이라고 한다. 이 때, tree들의 weight 합을 해당 tree packing의 value라고 한다.
Nash-Williams 정리에 의해, min-cut의 value가 $c$라면 value가 $c / 2$ 이상인 weighted tree packing이 존재함을 알 수 있습니다. 이 세팅에서 min-cut을 $2$-constrain하는 트리가 packing 안에 존재한다는 것은 쉽게 알 수 있지만, 다음의 정리는 그런 트리가 일정 비율 이상을 차지한다는 강력한 사실을 말해줍니다.
Theorem 1. $C$가 value가 $\alpha c$ 이하인 weighted cut이라고 하고 (이를 $\alpha$-minimum cut이라고 한다), $P$가 value $\beta c$인 weighted tree packing이라고 하자. 이 때, (weight 기준으로) $P$의 $\frac{1}{2}(3 - \frac{\alpha}{\beta})$ 비율 이상의 tree들이 $C$를 $2$-constrain한다.
$C$가 min-cut이고, $P$가 maximum tree packing인 경우 $\alpha = 1$이고, NW theorem에 의해 $\beta \ge \frac{1}{2}$이기 때문에 maximum tree packing의 절반 이상이 $C$를 $2$-constrain함을 알 수 있습니다. 따라서 maximum tree packing 안에서 $1/2$ 이상의 확률로 min-cut을 $2$-constrain하는 tree를 찾을 수 있습니다. 물론 maximum tree packing을 찾는 것 자체가 아직 어렵기 때문에 실제로는 이 정리를 다른 형태로 활용하고, 이는 뒤 챕터에서 보실 수 있습니다. 해당 Theorem의 증명을 봅시다.
Proof. $P$의 트리 $T$에 대해서, $x _ {T}$를 $T$와 $C$에 공통으로 속하는 간선의 개수라고 합시다. 이 때 $A$를 $x _ {T} \ge 3$인 트리들의 weight sum, $B$를 $x _ {T} \le 2$인 트리들의 weight sum으로 둡니다. 즉, $B \ge \frac{1}{2}(3\beta - \alpha)c$임을 보이면 충분합니다. 이 때 $A + B = \beta c$이고, 모든 $C$의 에지들은 $P$의 트리들에 의해 분할되므로, $3A + B \le \alpha c$를 추가로 얻습니다. 이후는 단순 계산. $\square$
Random Sampling
Blackbox
Random sampling 알고리즘에 있어, 다음 알고리즘들을 증명하지 않고 사용합니다.
Gab95. (Gabow 1995) 크기 $k$인 tree packing이 존재한다면, 이를 $O(mk \log n)$ 시간에 찾을 수 있다. 마찬가지로, min-cut을 $O(mc \log n)$ 시간에 찾을 수 있다.
Nag92. (Nagamochi-Ibaraki 1992) 임의의 sparse $k$-connectivity certificate을 $O(m + n\log n)$ 시간에 구할 수 있다. $G$의 subgraph $H$가 $G$의 sparse $k$-connectivity cerificate이라는 것은, $H$ total weight가 $kn$이고 크기가 $k$ 이하인 모든 $G$의 cut이 $H$에도 동일한 value를 가진다는 것을 말한다.
- 이로부터, sparse $c$-connectivity certificate을 구할 수 있다면 이 subgraph는 원래 그래프와 동일한 min-cut을 가집니다. 따라서, 앞으로 모든 algorithm에서 $m = O(nc)$를 가정할 수 있습니다.
Mat93 (Matula 1993). min-cut의 $3$-approximation을 $O(m + n)$ 시간에 계산할 수 있다. 즉, $[c, 3c]$ 사이에 있는 어떤 값을 선형 시간에 guess할 수 있다.
Goal of Sampling
Karger algorithm의 가장 핵심인 Random Sampling 부분입니다. Random sampling을 통해 achieve하고자 하는 바는, 적당한 상수 $\varepsilon$에 대해 다음을 만족하는 $G$의 subgraph $H$를 $O(m + n\log^{3} n)$ 시간 안에 만드는 것입니다.
- $H$의 간선은 $m’ = O(n\varepsilon^{-2} \log n)$개이다.
-
$H$의 minimum cut은 $c’ = O(\varepsilon^{-2} \log n)$이다.
- $G$의 minimum cut은 높은 확률로 $H$의 $(1 + \varepsilon)$-minimum cut이다.
편의를 위해 $\varepsilon = \frac{1}{6}$이라는 적당한 값을 잡아 봅시다. $H$의 maximum tree packing은 Gab95를 사용하면 $O(\varepsilon^{-4} n \log^{3} n)$ 시간에 구할 수 있고, 그 크기는 $O(\varepsilon^{-2}\log n)$일 것입니다 (by weight). 이 때, Theorem 1에 의해 높은 확률로 개중 $\frac{1}{2}(3 - \frac{1 + \varepsilon}{1 / 2}) = \frac{1}{3}$ 이상의 비율이 $G$의 min-cut을 $2$-constrain할 것입니다. 따라서 $O(\log n)$개의 트리를 시도해 보면 높은 확률로 min-cut을 $2$-constrain하는 트리를 잡아낼 수 있습니다. 따라서 전체 시간복잡도가 $O(T _ {2}(m, n) \log n + m + \varepsilon^{-4}n\log^{3} n)$이 됩니다.
Sampling Routine
Sampling 기법 자체는 매우 간단합니다. 특정한 확률 $p$를 잘 정해서, 각 간선을 $p$의 확률로 독립적으로 뽑기만 하면 됩니다. 단, 가중치 $w$인 간선들은 $w$개의 multi-edge로 간주하여 binomial distribution 하에서 sampling합니다.
Theorem 2. $p = 3(d+2)\ln n / (\varepsilon^{2} \gamma c) \le 1$이라고 하자. $\varepsilon > 0, \gamma \le 1$은 상수이다. ($\Theta(1)$) 이 때 $p$의 확률로 각 간선을 sampling해 만든 그래프 $H$는 $1 - n^{-d}$의 확률로 다음을 만족한다.
- $H$의 min-cut $c’$은 $O(\varepsilon^{-2} \log n)$이다. 이를 바탕으로, $H$의 sparse $c’$-connectivity certificate을 구하면 $H$의 간선 또한 $O(n\varepsilon^{-2} \log n)$개로 줄일 수 있다.
- $G$의 value $v$인 cut에 대해, 이 cut은 $H$에서 $[(1 - \varepsilon)pv, (1 + \varepsilon)pv]$의 value를 갖는다. value의 기댓값이 $pv$임에 주목하자. 특별히, $G$의 min-cut은 높은 확률로 $H$의 $(1 + \varepsilon)$-min cut이다.
증명은 Chernoff’s bound를 이용하면 가능합니다. 이는 독립적인 Bernoulli random variable의 합 (이 경우, $H$에도 포함되는 간선의 개수)이 그 기댓값에서 많이 벗어날 확률이 매우 낮다는 정리로, 디테일은 복잡한 계산이라 생략하겠습니다.
언뜻 단순해 보이는 rountine이지만 함정이 숨어 있습니다. $G$의 min-cut $c$에 대한 추정치가 있어야 $p$를 설정할 수 있기 때문이죠. 보조 인자 $\gamma$의 도움을 받아 생각해보면, 우리는 $G$의 min-cut에 대한 constant-factor underestimation 이 필요하다는 사실을 알 수 있습니다. 이는 Mat93을 이용하면 선형 시간에 계산할 수 있으므로, $\gamma \ge 1 / 3$을 얻을 수 있습니다. 다만 Mat93은 Nag92 등 여러 subroutine에 의존하는 알고리즘으로 구현이 복잡합니다. 여러 workaround가 있지만, 여기서는 Bhardwaj et al. (2020)의 방법을 소개합니다.
Lemma. 위의 조건에서 $\varepsilon \le \frac{1}{3}$, $\gamma \ge 6$을 만족한다고 하자. 이 때, $1 - \frac{1}{n^{d+2}}$의 확률로 $H$의 min-cut은 $(d+2)\ln n / \varepsilon^{2}$보다 작다.
증명은 동일하게 Chernoff bound로 됩니다. 역시 복잡한 계산일 뿐이니 생략합니다.
$\gamma = 1$인 경우 $H$의 min-cut의 기댓값은 $3(d+2)\ln n / \varepsilon^{2}$이고, 이 값의 $[1 - \varepsilon, 1 + \varepsilon]$배에서 벗어날 가능성이 매우 낮다는 것을 생각합시다. 즉, $\gamma \ge 6$인 경우는 해당 값을 한참 벗어난 것이라고 생각할 수 있습니다. 따라서 $\gamma$를 overestimate한 경우를 reject할 수 있습니다.
이제, $U \ge c$임이 보장되는 적당한 $U$값을 잡고 $\gamma c= U$로 두고, Gabow’s algorithm을 이용하여 $H$의 min-cut을 구합시다. 만약 $H$의 min-cut이 너무 작다면 $\gamma$에 $1 / 6$을 곱해서 반복합니다. 총 $\log (U / c)$ 번 정도의 iteration이 돌게 되지만 $H$의 min cut은 $O(\varepsilon^{-2} \log n / \gamma)$이고, Gabow95가 결과적으로 $O(m \varepsilon^{-2} \log n / \gamma)$ 시간 안에 돌게 됩니다. 그런데 $\gamma$가 등비수열을 따라 감소하므로, 이 값을 모두 합쳐도 $O(m \varepsilon^{-2} \log n + \varepsilon^{-4}n\log^{3} n)$ 시간에 skeleton을 만들 수 있다는 analysis를 얻을 수 있습니다. 또는 Nag92를 이용하여그래프 $H$의 $\gamma c$-connectivity certificate을 구하는 방법이 있습니다. 이는 매번 $O(m + n\log n)$ 시간 안에 동작하는 알고리즘이므로 $\varepsilon$-dependency가 줄어든 $O(m\log n + n\log^{2} n + \varepsilon^{-4} n\log^{3} n)$ 시간을 얻게 됩니다. 실제로 Bhardwaj의 구현체에서는 매번 다른 $\gamma$값에 따라 $O(mc \log n)$ tree packing algorithm을 실행시키고, 이에 따라 $O(m \varepsilon^{-2} \log^{3} n)$시간 복잡도가 발생하게 됩니다.
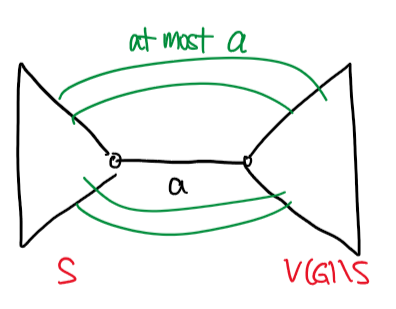
적당한 $U$값을 구하는 것 또한 신중하게 고려할 필요가 있는데요, min-cut이 $c$라고 할 때 $U = c \cdot n^{O(1)}$이 보장되어야 서로 다른 $\gamma$값이 $O(\log n)$번 나타난다는 것을 보장할 수 있습니다. Karger가 제시한 방법 중 하나는, 그래프의 Maximum spanning tree에서 가중치가 가장 작은 간선의 가중치를 $a$라고 하면 $a \le c \le n^{2} a$가 성립한다는 사실을 이용하는 것입니다. min-cut은 결국 Maximum spanning tree의 간선도 끊어야 할 테니 $c \ge a$이고, 가중치가 $a$인 간선이 끊는 트리를 기준으로 생각하면 이 cut의 크기가 $n^{2}a$를 넘지 못하는 이유 또한 생각해볼 수 있습니다. 따라서 $U = n^{2} a$로 두면 $O(\log n)$개의 $\gamma$값만 보게 된다는 사실을 보장할 수 있습니다.
2-Respecting Tree
이제 $O(\log n)$개의, min-cut을 $2$-constrain하는 tree packing을 얻어내는 데 성공했습니다. 이말인즉슨, 각 트리를 $2$-respect하는 cut들 중 높은 확률로 min-cut이 있다는 뜻입니다! 따라서, 고정된 트리 $T$에 대해 $T$를 $2$-respect하는 cut들 중 최솟값을 빠른 시간 안에 구해봅시다.
Notations
루트 있는 트리를 가정하고, 다음의 notation들을 정의합니다.
- $v^{\downarrow}$ : $v$의 서브트리에 있는 정점들 ($v$ 자신 포함)
- $v^{\uparrow}$ : $v$에서 루트로 가는 경로 ($v$ 자신을 포함)
- $f^{\downarrow}(v)$ : $f$가 각 정점마다 정의된 함수일 때, $\sum _ {u \in v^{\downarrow}} f(v)$.
또한, 정점들의 집합 $X, Y \subseteq V(G)$에 대해 $C(X, Y)$를 $X, Y$를 가로지르는 간선의 합으로 정의합니다. $X$와 $Y$가 서로소인 경우는 그 정의가 명확하나, 서로소가 아닌 경우에는 다음과 같이 clarify합니다.
- $x, y \in V(G)$에 대해, $C(x, y) := C({x}, {y}) = \mathrm{weight}(xy)$. $xy$가 간선으로 이어져 있지 않다면 $C(x, y) = 0$.
- $C(X, Y) = \sum _ {x \in X} \sum _ {y \in Y} C(x, y)$.
추가적으로,
- $C(S) := C(S, V(G) - S)$.
Case classification
루트가 있는 트리 $T$에서, 2-respecting cut들을 다음과 같은 기준으로 분류해 봅시다.
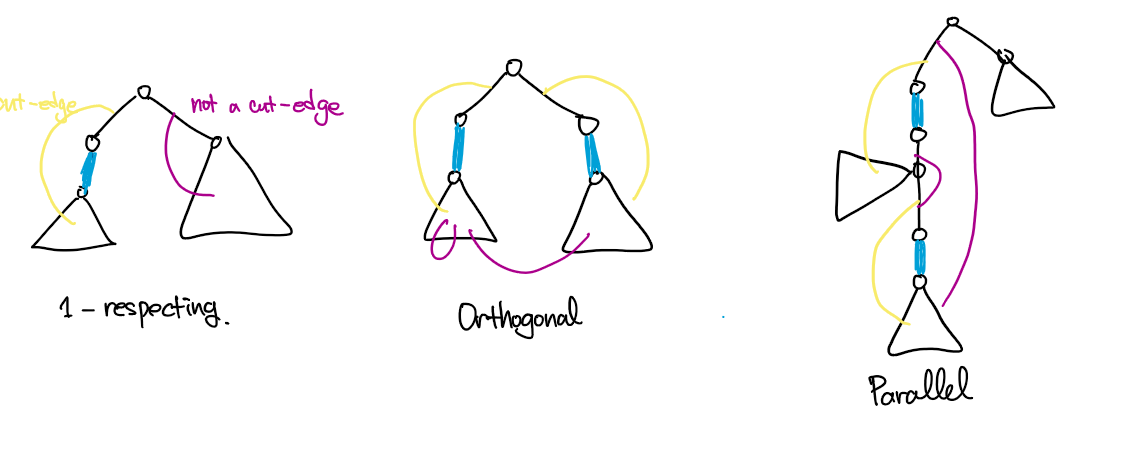
- $1$-respecting: 단 하나의 간선만 cut에 참여하는 경우입니다.
- Orthogonal: 조상-자손 관계가 없는 두 간선이 cut에 참여하는 경우입니다. 두 간선의 서브트리 사이를 이어주는 간선이 cut에 참여하지 않는다는 점을 주의해야 합니다. min-cut을 구하는 관점에서 보면, 서브트리 사이의 간선이 하나 이상 존재하는 경우만 보는 것이 이득임을 알 수 있습니다. 그렇지 않은 경우는 $1$-respecting case가 처리해주기 때문인데요, 이 관찰을 기억해 둡시다.
- Parallel: 조상-자손 관계인 두 간선이 cut에 참여하는 경우입니다. 조상 쪽의 정점을 $w$, 자손 쪽의 정점을 $v$라 할 때, 마찬가지로 $w^{\downarrow} - v^{\downarrow}$만 따로 떨어져나가는 경우만 고려해주면 됩니다.
$1$-respecting case: complete analysis
모든 $v$에 대해 $\mathcal{C}(v^{\downarrow})$ 를 계산하면 됩니다. 간단한 계산으로부터 다음을 얻을 수 있습니다.
$ \mathcal{C}(v^{\downarrow}) = \delta^{\downarrow} (v) - 2\rho^{\downarrow}(v).$
- $\delta(v) := \sum _ {u \in \mathcal{N} _ {G}(v)} \mathrm{weight}(uv)$. $v$에 ($T$가 아닌 $G$기준으로) 인접한 간선들의 weight 합으로, “weighted degree”라고 보면 좋습니다.
- $\rho(v) := \sum _ {LCA(x, y) = v} \mathrm{weight}(xy)$.
$\delta, \rho$는 간단한 DP로 $O(n)$에 계산할 수 있고, $f$를 알 때 $f^{\downarrow}$는 당연히 쉽게 알 수 있습니다.
Orthogonal case: model
모든 $v \notin w^{\downarrow}, w \notin v^{\downarrow}$인 $(v, w)$ pair에 대해 다음을 구해주면 됩니다. 편의상 $v \perp w$라고 씁시다. $ \mathcal{O}(v, w) := C(v^{\downarrow}) + C(w^{\downarrow}) - 2C(v^{\downarrow}, w^{\downarrow}) $
Parallel case: model
역시 $v \in w^{\downarrow}$에 대해, 유일하게 떨어지는 component인 $C(w^{\downarrow} - v^{\downarrow})$를 잘 구해주면 됩니다. 이 값은 정확히 다음과 같습니다. $ \mathcal{P}(v, w) := C(w^{\downarrow} - v^{\downarrow}) = C(w^{\downarrow}) - C(v^{\downarrow}) + 2C(v^{\downarrow}, w^{\downarrow} - v^{\downarrow}) = C(w^{\downarrow}) - C(v^{\downarrow}) + 2C(v^{\downarrow}, w^{\downarrow}) - 4\rho^{\downarrow}(v) $
$O(m\log^{2} n)$ time $2$-respecting cuts
결국 모든 $C(v^{\downarrow}, w^{\downarrow})$의 값을 다 구하면 문제를 해결할 수 있지만, 이 방법으로는 $O(m + n^2)$보다 나은 복잡도를 기대하기 어렵습니다. 따라서 자료 구조를 활용하여 고정된 $v$에 대해 $\mathcal{O}(v, w)$, $\mathcal{P}(v, w)$의 최솟값을 빠르게 구하는 방법을 고안할 필요가 있습니다.
Orthogonal case를 우선적으로 고려해보면, 각 $v$에 대해서 $v$-precut $C _ {v}(w)$를
$\mathcal{C} _ {v}(w) := \begin{cases} \mathcal{C}(w^{\downarrow}) - 2\mathcal{C}(v^{\downarrow}, w^{\downarrow}) & v \perp w \newline \infty & \text{otherwise} \end{cases}$와 같이 정의하고,
이로부터 얻을 수 있는 minimum $v$-precut $C _ {v}$를
$\mathcal{C} _ {v} := \min{ \mathcal{C} _ {v}(w) : \exists (v’, w’) \in E(G)\; \text{ s.t. } v’ \in v^{\downarrow} , w’ \in w^{\downarrow}}$로 정의합니다.
왜 단순히 $C _ {v} = \min_{w} C_{v}(w)$가 아니라 특수한 $w$들만 보아도 되는 것일까요? 이는 이전에 언급한 관찰의 결과로, $v^{\downarrow}$와 $w^{\downarrow}$를 잇는 간선이 없는 경우는 $1$-respecting cut에서 이미 걸러졌기 때문입니다. 놀랍게도 이러한 케이스 처리가 전체 시간을 줄이는 데에 큰 도움을 줍니다.
이제 각 $v$에 대한 $C _ {v}$를 빠른 시간에 구할 수 있다면 $\min _ {v} (C(v^{\downarrow}) + C _ {v})$를 구하면 됩니다. $C _ {v}$를 구하기 위해 Link-Cut Tree와 Bough decomposition을 도입할 텐데요, 이 둘을 이용해서 Orthogonal case를 풀고 자연스레 Parallel case 또한 처리하는 흐름으로 진행해 봅시다.
Adopting Link-Cut Tree
Dynamic tree 중 하나인 Link-Cut Tree를 데려옵니다. 이 자료구조에 대해 깊이 이해할 필요 없이, 다음을 $O(\log n)$ 시간에 지원하는 자료구조로 생각하면 됩니다.
-
각 정점마다 값이 정의된 배열
val[]을 관리합니다. AddPath(v, x): $i \in v^{\uparrow}$에 대해val[i] += x.MinPath(v): $\min _ {i \in v^{\uparrow}} val[i]$ 을 구합니다.
각 $w$에 대해 val[w]를 $C(w^{\downarrow})$로 초기화하고, link-cut tree를 통해 $-2C(v^{\downarrow}, w^{\downarrow})$만큼의 변화를 val[]에 뿌려 줍니다.
Bough decomposition
“Bough decomposition”이라는 개념은 Karger 이외에는 용례를 찾기 힘든 tree decomposition입니다. 각 Bough는 리프에서 루트로 향해 가다가 “자식이 둘 이상인 정점을 만나기 직전까지의 경로”로 정의됩니다. 물론 그 전에 루트를 도달한다면 루트를 포함하는 경로로 생각할 수 있습니다.
모든 Bough를 그 부모 (처음으로 만나는 자식이 둘 이상인 정점)에게 contract시키면, contracted tree의 리프 개수는 원래 트리의 절반 이하가 됨을 알 수 있습니다 .따라서 $O(\log n)$번의 contraction step을 통해 Bough decomposition이 완성됩니다. 즉, $C _ {v}$의 값을 $v$가 leaf인 경우, bough 위에 있는 경우, contracted graph 안에 있는 경우를 나누어 다룰 수 있으면 됩니다.
A Leaf
$\mathcal{C}(v, w^{\downarrow})$를 계산하기 위해, $v$의 이웃 $u \in \mathcal{N} _ {G}(v)$ 에 대해 정점 $x \in u^{\uparrow}$ 의 $C _ {v}(x)$는 $-2\mathcal{C}(v, u)$만큼 영향을 받는 것을 확인할 수 있습니다. 이를 AddPath로 구현합니다. 또한, 각 $C _ {v}$를 구하기 위해서는 $u \in N _ {G}(v)$에 대해 $\min _ {x \in u^{\uparrow}} C _ {v}(x)$들을 모아 최솟값을 취해주는 것으로 충분합니다. 이를 MinPath로 구현합니다.
def LocalUpdate(v):
AddPath(v, infinity) # to guarantee orthogonality, make v^{up} ignorable
for u in neighbor _ G[v]:
AddPath(u, -2*C(v, u))
ret = infinity
for u in neighbor _ G[v]:
ret = min(ret, MinPath(u))
return ret
LocalUpdate함수는 leaf $v$에 대해 $C _ {v}$를 반환하고, link-cut tree에 $O(\deg _ {G}(v))$ 번 쿼리를 날립니다.
A Bough
$v$가 bough에 있는 경우, $v$는 리프이거나 유일한 자식 $u$를 가집니다. 이 때, 다음의 보조정리를 이용할 수 있습니다.
Lemma. $C _ {v} = C _ {u}$이거나, $C _ {v} = C _ {v}(x)$를 만족하는 $w \in N _ {G}(v), x \in w^{\uparrow}$가 존재한다.
Proof. $C _ {v} = C _ {v}(y)$를 만족하는, $v$의 이웃을 하나도 subtree에 포함하고 있지 않은 $y$가 존재한다고 합시다. 이 경우 $C _ {v} = C _ {u}$임을 보이면 충분합니다.
이 때, $v$와 $y^{\downarrow}$ 사이에는 간선이 없으니 $C(u^{\downarrow}, y^{\downarrow}) = C(v^{\downarrow}, y^{\downarrow})$입니다. 따라서 $C _ {u} \le C _ {u}(y) = C _ {v}(y) = C _ {v}$인 한편, 임의의 $x$에 대해 $C(u^{\downarrow}, x^{\downarrow}) \le C(v^{\downarrow}, x^{\downarrow})$가 성립하므로 $C _ {u}(x) \ge C _ {v}(x)$이고, $C _ {u} \ge C _ {v}$이므로 $C _ {u} = C _ {v}$를 얻습니다. $\square$
따라서 다음의 MinPreCut 함수로 모든 Bough의 Min-PreCut을 계산할 수 있습니다.
def MinPreCut(v):
if v is a leaf:
return LocalUpdate(v)
u = child(v)
x1 = MinPreCut(u) # Modifies some val[] entries.
x2 = LocalUpdate(v)
return min(x1, x2)
Contraction
여러 개의 bough들을 독립적으로 다루기 위해서, 각 쿼리들은 사용이 끝난 후에 자연스럽게 반대 부호의 값을 더해 주어 cancel해야 합니다.
어떤 정점 $v$가 자식으로 bough $B$를 가질 때, $B$에서 나가는 간선들을 모두 $v$에서 나가는 간선으로 바꾸면 – 즉, $B$의 간선들을 모두 contract하면 – 이후 동일하게 문제를 풀 수 있습니다. contraction을 해주면서 간선을 옮기는 데는 $O(m)$ 시간밖에 들지 않습니다. 또, Link-Cut Tree에 쿼리를 보내는 횟수도 degree의 합에 비례하는 $O(m)$번 이므로, MinPreCut들을 이용해 Bough들의 $C _ {v}$를 계산하는 것은 $O(m \log n)$ 시간이면 충분합니다. Bough decomposition에서 총 $\log n$번만 contraction을 수행해주면 되므로 전체 수행 시간은 $O(m \log^{2} n)$입니다.
The Parallel Case
아직 기뻐하기는 이릅니다. Parallel case를 처리할 부분이 남아있습니다. 역시 각 $v$에 대해 $w$와 관련된 항만 뽑아내면, $C _ {v}(w) := \min _ {w \in v^{\uparrow}} C(w^{\downarrow}) + 2C(w^{\downarrow}, v^{\downarrow})$를 minimize하면 됩니다.
- Leaf $v$: $u \in N _ {G}(v)$에 대해
AddPath(u, 2C(v, u))를 호출해줍니다. 마지막에MinPath(v)를 구해주면 됩니다. - $v$ on a Bough: leaf와 동일하게
AddPath와MinPath를 호출하면 됩니다.
따라서, Orthogonal case에 비해 훨씬 간편하게 $2$-respecting cut들 중 최솟값을 구할 수 있습니다. 전체 시간복잡도는 $O(m \log^{2} n)$입니다.
Wrap-Up & Implementation notes
이 글에서 다음과 같은 사실들을 알아보았습니다.
- $T _ {2}(m, n) = O(m \log^{2} n)$. 이는 2020년에 이르러 $O(m \log n)$으로 개선되었습니다.
- $O(T _ {2}(m, n)\log n + m + n \log^{3} n)$ 시간에 Min-Cut을 구하는 randomized algorithm이 존재한다.
- 적당히 작은 cut과 적당히 큰 tree packing에 대해, 일정 비율 이상의 tree는 해당 cut을 $2$-respect한다.
- Random sampling을 통해 cut value를 보존하는 sparse subgraph를 만들 수 있다.
Bhardwaj는 이 알고리즘에 대한 사실상의 첫 구현체를 발표했는데요, 몇가지 workaround가 들어 있습니다.
- 복잡한 Gabow’s algorithm 대신, 같은 복잡도를 가진 Plotkin (1991)의 알고리즘을 이용하여 충분히 큰 tree packing을 구합니다.
-
Link-Cut Tree + Bough decomposition 대신, Heavy-light decomposition과 binary search tree를 이용한 $O(m \log^{4} n)$ implementation을 사용합니다.
- $\varepsilon$ 값을 조정하는 것이 까다롭습니다. 논문에서는 $3$개의 다른 값을 사용합니다.
현재는 $n = 2500$ case에서 $10^{2}$초 정도가 걸릴 정도로 느린 알고리즘인데요, 코딩에 자신이 있으시다면 performance 개선을 꿈꿔보시는 것도 좋을 듯합니다.
Further Reading
Karger 3부작. 이 글과의 관련도는 2000 > 1999 » 1996순입니다.
- Karger 1996 Random sampling in Graph Optimization Problems: Karger의 졸업논문입니다. 기존 방법에 대한 풍부한 리뷰가 있습니다.
- Karger 1999 Random sampling in Cut, Flow, and Network Design Problems: Edge sampling을 하는 방법이 여기 등장합니다
- Karger 2000 Minimum Cuts in Near-Linear Time: 이 글에서 리뷰한 논문입니다.
Tree packing.
- Gabow 1995 A Matroid Approach to Finding Edge Connectivity and Packing Arborescences: 자체로도 매우 어려운 알고리즘이라고 알고 있습니다.
- Plotkin 1991 Fast approximation algorithms for fractional packing and covering problems. Gabow의 알고리즘보다 간단하지만 크기가 작은 approximate tree packer입니다.
- Bhardwaj 2020 A Simple Algorithm for Minimum Cuts in Near-Linear Time: Tree packer가 실제 구현에서 어떻게 쓰이는지를 보다 구체적으로 볼 수 있습니다. 물론 전체 문제에 대한 구현법도 포함되어 있습니다.
Sparse $k$-connectivity Certificate
- Nagamochi 1992 A linear-time algorithm for finding a sparse k-connected spanning subgraph of a k-connected graph
기존 방법론에 대한 리뷰 + 최신 성과들
- GMW 2019 Minimum cut in $O(m \log^{2} n)$ time
- Mukhopadyay 2020 Weighted Min-Cut: Sequential, Cut-Query and Streaming Algorithms