Ray Casting Algorithm의 이분 탐색을 이용한 응용
Ray Casting Algorithm
(단순) 다각형과 점이 주어졌을 때, 점이 다각형 안에 있는지 판정하는 문제는 계산 기하학뿐 아니라 컴퓨터 그래픽스에서도 중요한 문제이다. 이를 해결하는 대표적인 알고리즘이 Ray casting algorithm이다. 가장 간단한 버전의 ray casting algorithm은 다음과 같은 문제를 푸는 데 사용된다.
“2차원 좌표평면 위에 단순 다각형 $(x_0, y_0), \cdots, (x_N, y_N)$이 있다. 마찬가지로 2차원 좌표평면 위에 점 $P=(x, y)$가 주어질 때, 이 점이 다각형 안에 있는지 밖에 있는지 판정하라.”
Ray casting algorithm은 이를 다음과 같은 아이디어로 판정한다.
- 다각형 바깥에 있는 아무 점이나 들고 와서 $O$ 라는 이름을 붙이자.. (x좌표가 $\min_{0 \le i \le N}{x_i}$ 보다 작은 점을 들고 오면 확실하다.)
- $O$ 와 $P$ 를 잇는 선분을 긋는다. 만약 선분과 다각형이 홀수 번 교차한다면, $P$ 가 다각형 안에 있다. 선분과 다각형이 짝수 번 교차한다면, $P$가 다각형 밖에 있다.
물론 위 알고리즘은 얼핏 생각했을 때는 간단하지만, 코너 케이스가 많다. 다각형의 꼭짓점이 선분 위에 있을 때, 다각형의 변이 선분 위에 있지만 겹치지는 않을 때, 선분과 다각형의 변이 겹칠 때 등등 골치아픈 상황이 많은데, 간단하게 해결할 수 있는 여러 방법이 있다. 이는 이 글의 주제는 아니므로 다루지는 않지만, 이 링크에 설명되어 있으니 참조하면 좋다. 이 알고리즘의 시간 복잡도는 $O(N)$이 된다.
Ray Casting Algorithm의 응용
위 알고리즘에서, 다각형이 볼록하다면 선분 $OP$ 와 다각형은 많아야 두 번 교차한다. 우리가 처음에 아무 점으로 정했던 점 $O$를, $P$와 y좌표가 같은 점으로 정하기로 하자. 그러면 물론 선분 $OP$ 와 다각형의 교점도, $P$ 와 y좌표가 같다. 우리는 ‘웬만하면’ 다각형에 어떤 y좌표를 지닌 점은 많아야 두 개임을 알고 있다. 그 두 점을 찾으면, 각각이 선분 $OP$ 위에 있는지도 쉬이 알 수 있을 것이다. 이는 다음과 같이 이분 탐색을 이용한 방법으로 구할 수 있다.
- 다각형에서 y좌표가 가장 작은 점과 가장 큰 점을 구한다. 둘 모두, 다각형의 어떤 꼭짓점으로 나타날 것이다.
- 이제, 다각형은 이 두 점을 기준으로 왼쪽과 오른쪽으로 나뉜다.
- 왼쪽과 오른쪽 각각에서 y좌표에 대해 이분탐색을 수행해, 다각형에서 $P$ 와 y좌표가 같은 점이 속하는 변을 찾는다.
- $OP$ 와 해당 변이 교차하는지 판별한다.
주의해야 할 경우가 한 가지 있다. $P$ 와 y좌표가 같고 x축과 평행한 변이 다각형에 있을 경우인데, 구현에 따라 이 경우를 처리하지 못할 수도 있다. 아래 그림과 같이, 다각형을 왼쪽과 오른쪽 부분으로 나눌 때, x축과 평행한 변을 제외하고 나누어주는 것이 중요하다.
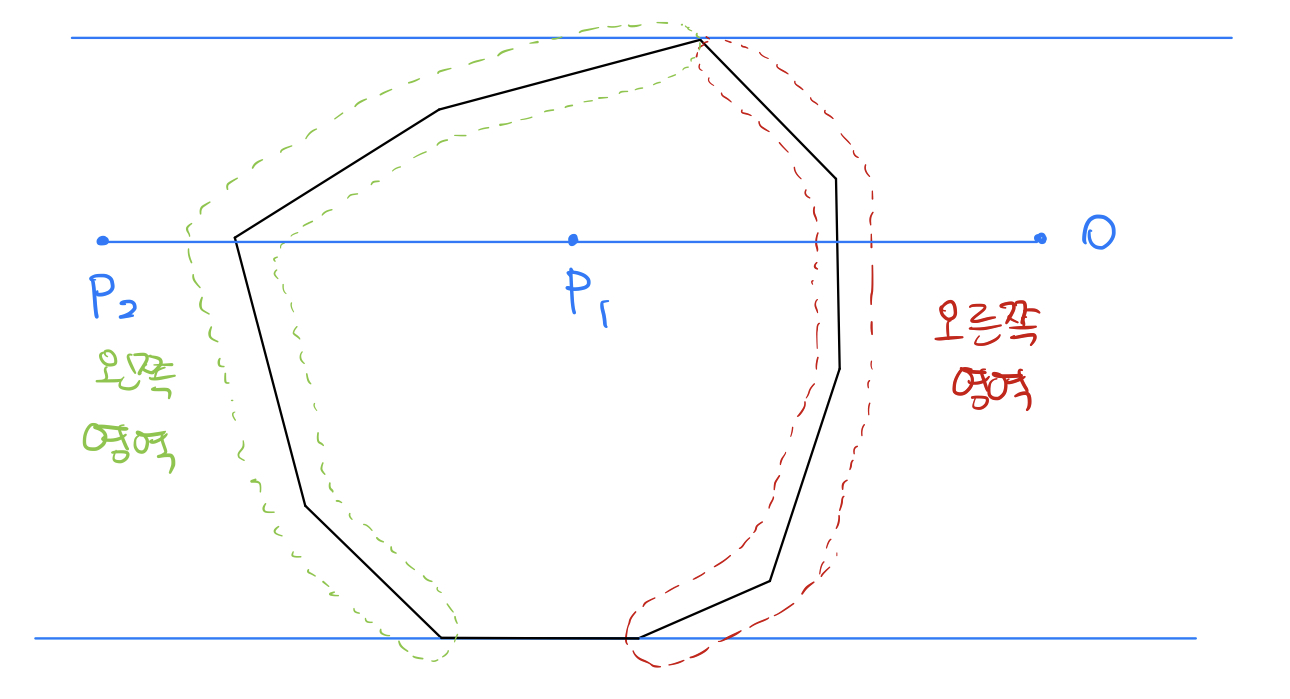
다른 관점
위 그림에서, y축에 평행한 두 개의 직선을 이용해서 다각형을 왼쪽과 오른쪽 부분으로 나누었다. 사실은, 그렇게 하는 대신 아래 그림과 같이 점 $P$ 에서 다각형으로 접선을 그어, 다각형을 접선의 ‘안쪽’과 ‘바깥쪽’으로 나눌 수 있다. 각 영역에서 직선 $OP$ 와 교차하는 변은 하나씩 존재한다. 따라서 앞서 다각형의 왼쪽과 오른쪽 부분에서 직선 $OP$와 교차하는 변을 찾기 위해 이분 탐색을 수행했던 것처럼, 다각형의 안쪽과 바깥쪽에서 직선 $OP$ 와 교차하는 변을 찾기 위해 이분 탐색을 수행할 수 있다. 물론, 이 이후에 실제로 ‘선분 $OP$’가 다각형과 교차하는지 판별해서 교차 횟수를 세 주는 것은 동일하다.
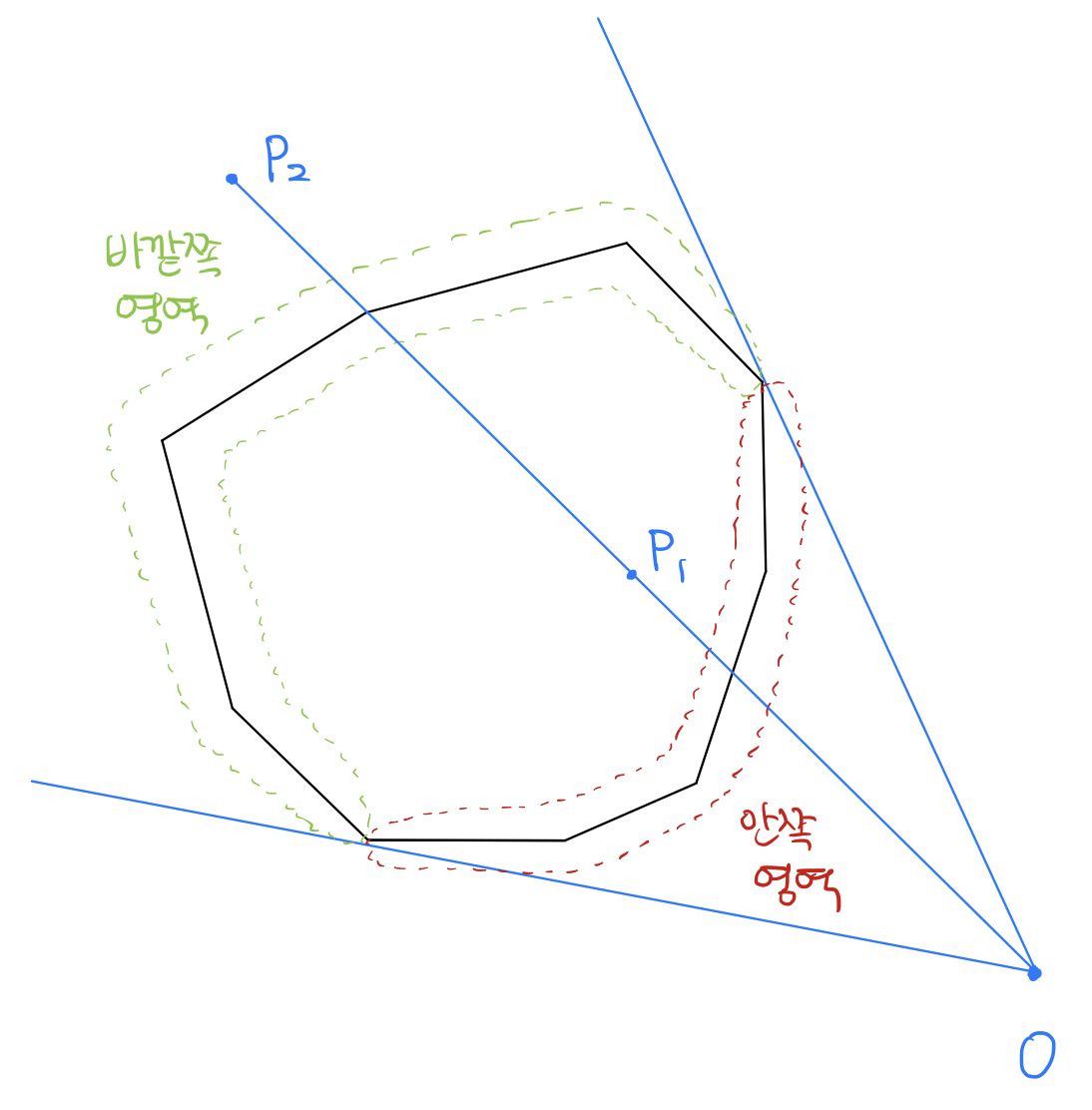
이 때에는, 단순히 좌표를 비교하는 방법으로는 여기서 극단적으로 점 $O$ 를 당겨 잡으면 이분 탐색을 단 한 번만 수행할 수 있다. 점 $O$를 다각형의 한 꼭짓점으로 잡으면, 다각형의 안쪽 영역에는 점 $O$와 인접한 두 개의 변만이 포함된다. 아래 그림에서 점 $P$가 직선 $OA$나 직선 $OB$ 밖에 있는 상황만 아니면, 점 $P$는 무조건 접선 바깥쪽에 있고, 이 안에서 직선 $OP$가 교차하는 변을 찾기 위해 이분 탐색을 수행한다.
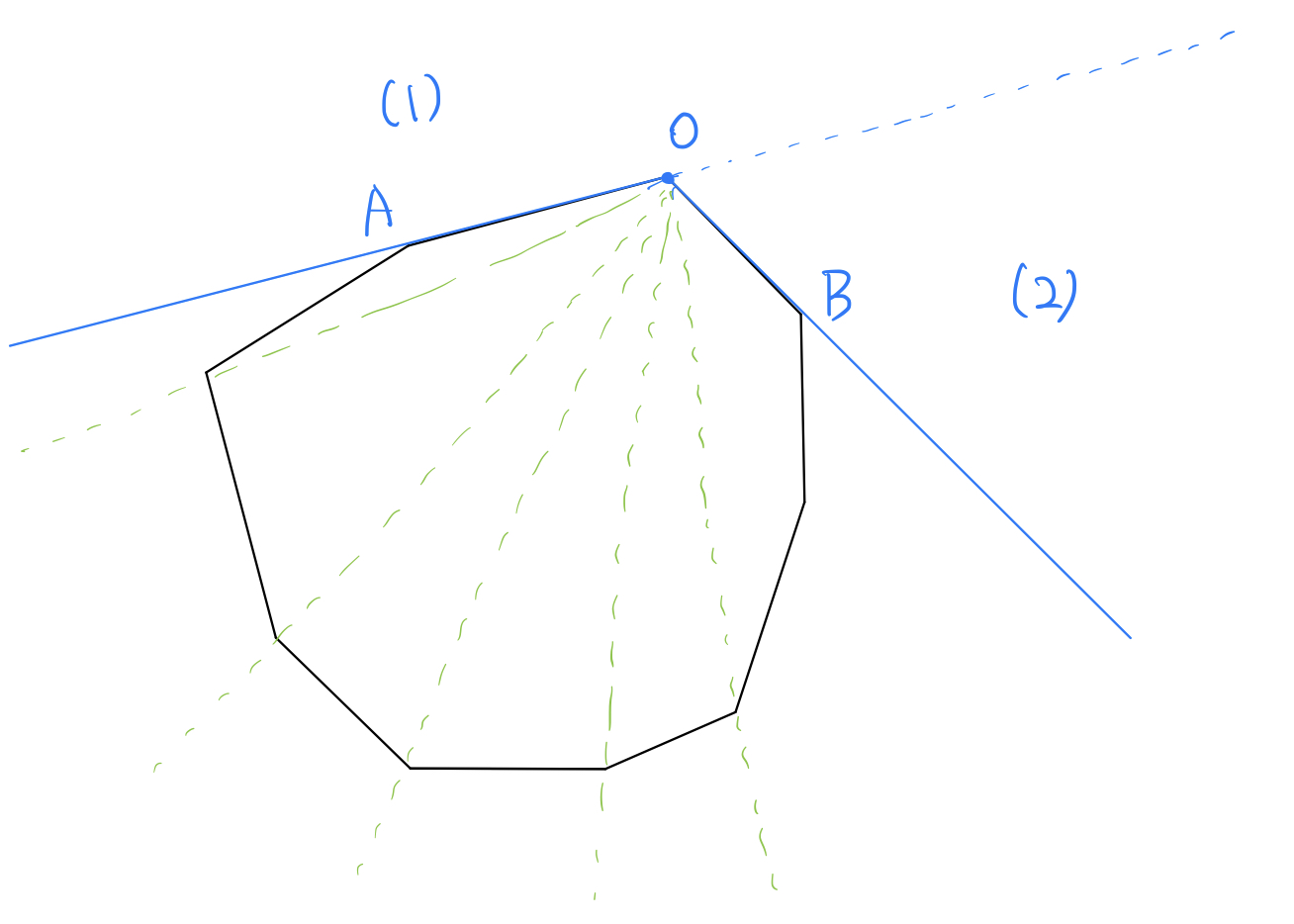
다각형이 위 그림 3과 같이 삼각분할 되어 있다고 생각하면 시각적으로 편해지는 것 같다. 점 $P$가 영역 (1)과 영역 (2)에 있는 경우를 제외하고 나서, 점 $P$가 이 삼각 분할 위의 어떤 영역에 속하는지를 판별한다고 보면 좋다.
결국은 같은 알고리즘을 점 $O$를 잡는 위치에 따라 다른 방법으로 구현할 수 있다.. 첫 방법은 사실 점 $O$를 좌표 $(\infty, y)$에 두고 생각하는 것과 동일하고, 두번째 방법은 점 $O$를 한 꼭짓점 위에 두고 생각했다. 결국은 이분 탐색 한 번 또는 두 번만을 수행하므로, 총 시간 복잡도는 $O(\log N)$이다.
연습 문제
- https://www.acmicpc.net/problem/9875
위 알고리즘을 있는 그대로 연습할 수 있는 연습문제이다. 팀 B의 각 점들이 팀 A의 점들의 볼록 껍질 안에 포함되는지 판별하고, 팀 A의 각 점들이 팀 B의 점들의 볼록 껍질 안에 포함되는지 판별한다.
- https://www.acmicpc.net/problem/3878
검정 점들과 흰 점들을 분리할 수 있다는 것은, 검정 점들의 볼록 껍질 $B$와 흰 점들의 볼록 껍질 $W$를 분리할 수 있다는 것이다. 두 다각형의 위치 관계는 언제나 아래 세 가지 중 하나이다.
- 교차한다.
- 하나가 다른 하나 안에 있다.
- 분리할 수 있다.
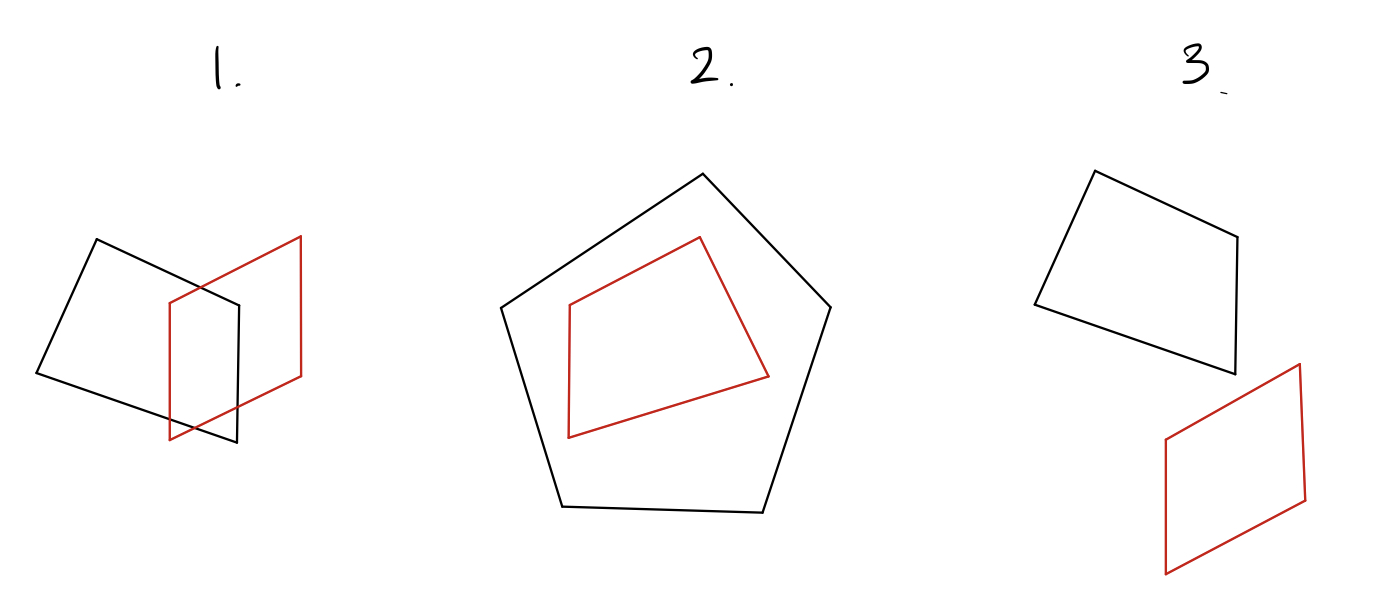
1번에 해당되는지는 쉽게 판단할 수 있다. 선분 교차 판별을 할 줄 안다면, 그냥 $A$에 속하는 선분들 각각과 $B$에 속하는 선분들 각각이 교차하는지 총 $O(N^2)$의 시간복잡도로 판별하면 된다. 하지만, 문제에서는 요구하지 않지만 두 다각형이 모두 볼록하기 때문에 $O(N \log N)$에 할 수도 있다. 우리가 이때까지 해온 것이 ‘다각형과 선분이 교차하는 점이 몇 개 있는지 판별’하는 것 아니었던가?
2번에 해당되는지 판별하는 것은, 가장 간단하게는, 위의 ‘Cow curling’ 문제를 풀면 된다. 한 껍질의 모든 점이 다른 껍질 안에 들어있는지 판별하면 되는 것이니.
따라서, 총합 $O(N \log N)$에 이 문제를 해결할 수 있다. 귀찮다면, 1번의 판별을 $O(N^2)$에 수행해도 문제를 해결할 수 있다.