헝가리안 알고리즘
안녕하세요?
오늘은 헝가리안 알고리즘(Hungarian Algorithm)에 대해 살펴보겠습니다.
헝가리안 알고리즘은 가중치가 있는 이분 그래프(weighted bitarted graph)에서 maximum weight matching을 찾기 위한 알고리즘입니다.
이분 그래프의 Matching
M이 edge들의 부분집합이고, 모든 vertex들에 M에 속한 edge가 최대 한 개 연결되어 있을 때, 이러한 M을 그래프의 matching이라고 합니다. 일반적인 이분 그래프에서 최대 매칭은 최대 유량을 구하는 알고리즘을 통해 구할 수 있다는 사실이 잘 알려져 있습니다.
Matching M의 weight는 M에 속한 edge들의 가중치의 합으로 정의할 수 있습니다. 이제 우리는 Matching 중 이 가중치의 합이 가장 것을 찾는 것을 목표로 하겠습니다.
먼저, 모든 가중치는 모두 음이 아닌 정수라고 가정하겠습니다. 사실 만약 음의 가중치를 가지는 간선이 있다면 이 간선을 고를 이유가 전혀 없으므로, 그냥 없다고 생각해도 무방합니다.
만약 무조건 n개의 매칭을 만들어야 하는 등의, 음의 간선을 고를 수밖에 없는 상황이더라도, 이 경우에는 모든 가중치들에 적당한 수를 더해 음이 아닌 정수로 만들어주어도 결과가 바뀌지 않으므로 모든 간선이 음이 아닌 정수라고 가정하겠습니다.
또한, 편의상 주어진 이분그래프는 나누어지는 두 집합의 크기가 같은 완전이분그래프라고 가정하겠습니다. 만약 이 조건을 만족하지 않더라도, 몇 개의 가상의 노드를 추가하고 가중치 0인 간선들을 추가하면 결과값이 바뀌지 않는 채로 쉽게 이러한 형태로 만들 수 있으므로 이 또한 일반성을 크게 잃는 가정은 아닙니다.
이제 아래와 같은 형태가 되었습니다.
그림 1. 완전 이분 그래프의 예시
임의의 매칭 M이 있을 때, 아래와 같은 용어를 먼저 정의하겠습니다.
matched: vertex v가 M에 속한 edge 중 어느 하나의 끝점일 때, 이 vertex를 matched 되었다고 하겠습니다. 그렇지 않은 경우는 free vertex라고 하겠습니다.
다음으로, 그래프 위의 특정 경로가 M에 속한 edge와 E - M에 속한 edge를 번갈아가면서 지날 때, 이러한 경로를 alternating path라고 하겠습니다. Alternating path 중 시작점과 끝점이 모두 free vertex일 때 이를 augmenting path라고 하겠습니다.
Augmenting path는 아주 중요한데, 해당 path에 속한 edge를 서로 바꾸어주면 크기가 1 큰 matching을 만들어낼 수 있기 때문입니다.
아래 예시를 보시면 조금 더 이해하기 쉬울 것이라 생각합니다.
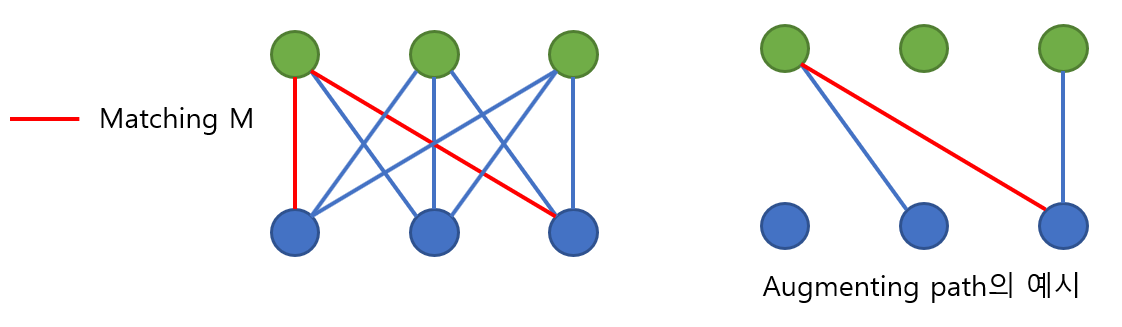
그림 2. Matching과 augmenting path의 예시
마지막으로, 어떤 rooted tree가 root에서 시작하는 모든 경로가 alternating path일 경우, 이를 alternating tree라고 하겠습니다.
헝가리안 알고리즘
헝가리안 알고리즘은 각 vertex마다 적당한 수를 labeling합니다.
집합 X, Y에 대해서 $l(x) + l(y) \ge w(x, y)$를 만족할 때, 이러한 labeling은 feasible하다고 합니다.
이러한 어떠한 labeling l이 되어있을 때, $l(x) + l(y) = w(x, y)$인 edge들을 모아놓은 것을 이러한 labeling의 Equality Graph라고 합니다.
예를 들어, 아래와 같은 그래프에서 하나의 feasible labeling과 그 때의 Equality Graph를 나타낸 그림입니다.
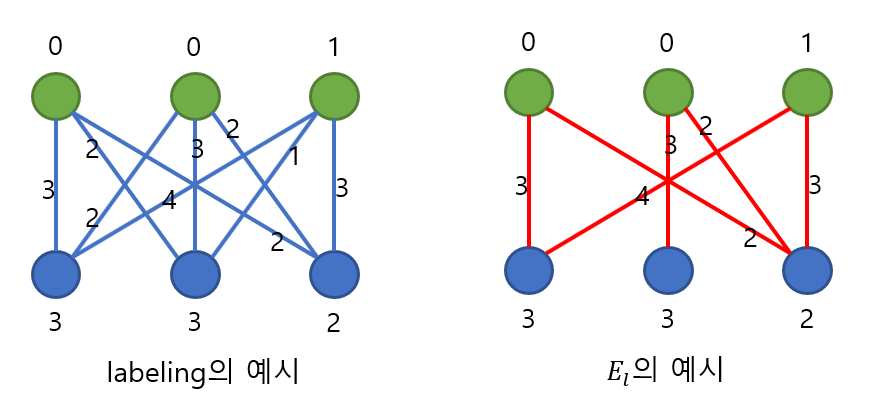
그림 3. Feasible labeling와 Equality Graph의 예시
이 때, 다음과 같은 상당히 자명한 정리를 찾아낼 수 있습니다.
Labeling l이 feasible하고, $M \subseteq E_l$인 matching M이 perfect matching이면 매칭 M은 max-weight matching이다
헝가리안 알고리즘은 위 정리를 기반으로 작동합니다. 정확히는, Labeling을 계속 feasible한 상태로 유지하며 matching의 크기를 점점 늘려나가 최종적으로 matching이 perfect matching이 되도록 만드는 것입니다.
다시 말해, 알고리즘의 동작 과정은 아래와 같은 순서로 동작합니다.
-
임의의 feasible한 labeling l을 찾고, $E_l$에서 임의의 matching M을 찾는다.
-
M이 perfect matching이 될 때까지 아래를 반복한다.
2-1. E_l에서 M의 augmenting path를 찾은 후, M의 크기를 증가시킨다.
2-2. 더 이상 Augmenting path를 찾지 못할 경우, labeling l을 l’로 교체한다. 이 때 $E_l \subset E_{l’}$을 만족하도록 한다.
2-1과 2-2에서, 최소한 M의 크기 혹은 $E_l$의 크기 둘 중 하나는 무조건 증가하므로, 해당 알고리즘은 언젠가 반드시 종료하게 됨을 알 수 있습니다.
이제 상당히 추상적으로 표현되어 있는 각 과정을 상세히 알아보겠습니다.
Feasible한 Labeling 찾기
1번 과정의 feasible한 labeling l과 해당 라벨이 만드는 Equality Graph에서 임의의 matching을 찾는 것은 매우 쉽습니다.
보통은, 아래와 같은 식으로 초기값을 할당합니다.
X에 속한 vertex의 경우: $l(x) = \max_{y\in Y}{w(x,y)}$
Y에 속한 vertex의 경우: $l(y) = 0$
이렇게 할당할 경우 모든 edge마다, $w(x,y) \le l(x) + l(y)$를 만족하는 것을 쉽게 확인 가능합니다.
Improving Labelings
2-2번 과정에서, labeling l을 l’로 교체하는 작업입니다.
X의 부분집합 S에 대해, S의 원소와 Equaliry Graph를 통해 이어진 Y의 원소들의 집합을 $N_l{S}$라고 합시다. 이 때, 다음과 같은 작업을 해줍니다.
$\alpha_l = \min_{x \in S, y \notin N_l(S)}{l(x) + l(y) - w(x,y)}$라고 할 때
$v \in S$이면, $l’(v) = l(v) - \alpha_l$
$v \in N_l(S)$이면, $l’(v) = l(v) + \alpha_l$
위 두 경우가 아니면, $l’(v) = l(v)$
이러한 작업을 진행해 줄 경우, 기존 $E_l$에 속해있는 edge에 대해서는 l(x) + l(y)가 보존되므로 $E_l’$에도 계속 속해있게 됩니다. 반면, 최소 하나 이상의 edge가 $E_l’$에 새로 추가되게 됩니다.
Augment path 찾기
마지막은 Augment path를 찾는 부분입니다. 헝가리안 알고리즘에서는 매칭 M이 perfect하지 않을 경우 아래와 같은 방법을 통해 Augment path를 찾습니다.
-
X에서 free vertex u를 하나 골라 $S = \lbrace u\rbrace$, $T = \emptyset$으로 놓습니다.
-
이후 $N_l(S) \neq T$임을 유지합니다. 만약 $N_l(S) = T$일 경우, 위에서 설명한 Improve Labeling을 통해 $N_l(S) \neq T$가 되도록 유지합니다.
-
$N_l(S) \neq T$임이 보장된 상태에서, $y \in N_l(S) - T$인 y를 하나 뽑습니다.
3-1. y가 free vertex이면, u에서 y로 가는 경로가 augmenting path이므로 해당 경로를 이용해 M을 증가시킵니다. 이후 1번부터 반복합니다.
3-2. y가 matched vertex이면, y가 매칭되어 있는 쌍을 z라 하고, y와 z를 alternating tree에 추가시켜줍니다. 이후 $S = S \cup \lbrace z \rbrace$, $T = T \cup \lbrace y \rbrace$로 놓은 뒤 2번 과정부터 반복합니다.
시간 복잡도 분석
구현 시에는 slack이라는 또다른 배열을 하나 유지시켜 시간복잡도의 향상을 꾀합니다.
$slack_y = \min_{x \in S}{l(x) + l(y) - w(x,y)}$를 저장해둡니다. 이를 저장함으로서 얻을 수 있는 효과는 $\alpha_l$를 $O(V)$만에 계산 가능하다는 점입니다.
각 phase가 한 번 진행될 때마다 M의 크기가 1씩 증가하며, M이 perfect matching이 된 경우 M의 크기는 V이므로 phase는 최대 V번 반복됩니다.
각 phase마다 slack 배열을 update시키는 비용을 살펴보도록 하겠습니다.
slack 배열은 S에 원소가 추가될 때마다 업데이트되어야 합니다. 원소의 추가는 최대 V번 일어날 수 있고, 이 때마다 업데이트시키는 비용은 O(V)이므로 각 phase마다 $O(V^2)$만큼의 비용으로 업데이트시킬 수 있습니다.
$\alpha_l$을 계산하고 업데이트시키는 데에 소모되는 비용을 살펴보겠습니다. 계산하는 비용은 slack 배열을 통해 O(V)에 수행 가능하며, alpha를 통해 Improve Lableing을 진행할 때마다 최소 하나의 vertex가 $N_l(S)$에 속하게 되므로 이 또한 최대 O(V)회 일어납니다. 따라서 $\alpha_l$과 관련된 부분은 한 phase마다 $O(V^2)$만큼의 시간이 소요됩니다.
따라서 알고리즘의 총 수행시간은 $O(V^3)$인 것을 알 수 있습니다. 비슷한 결과를 얻을 수 있는 MCMF 등의 알고리즘의 수행시간인 $O(V^4)$에 비해 빠른 속도임을 알 수 있습니다.
구현
아래는 헝가리안 알고리즘을 구현한 코드입니다.
#define N 500
#define INF 987654321
int w[N][N];
int match_x[N];
int match_y[N];
int l_x[N], l_y[N];
bool s[N], t[N];
int slack[N];
int slack_x[N];
int tree_x[N];
int tree_y[N];
void print(int n) {
cout << "l_x: ";
for (int i = 0; i < n; ++i) cout << l_x[i] << ' ';
cout << '\n';
cout << "l_y: ";
for (int i = 0; i < n; ++i) cout << l_y[i] << ' ';
cout << '\n';
}
int hungarian(int n) {
memset(match_x, -1, sizeof(match_x));
memset(match_y, -1, sizeof(match_y));
int ret = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
l_x[i] = max(l_x[i], w[i][j]);
}
}
memset(l_y, 0, sizeof(l_y));
int m = 0;
while (m != n) { // repeat at most V times
memset(tree_x, -1, sizeof(tree_x));
memset(tree_y, -1, sizeof(tree_y));
memset(s, 0, sizeof(s));
memset(t, 0, sizeof(t));
int s_start;
for (int i = 0; i < n; ++i) { // O(V)
if (match_x[i] == -1) {
s[i] = 1;
s_start = i;
break;
}
}
for (int i = 0; i < n; ++i) { // init slack
slack[i] = l_x[s_start] + l_y[i] - w[s_start][i];
slack_x[i] = s_start;
}
here:
int y = -1;
for (int i = 0; i < n; ++i) { // compare: O(V)
if (slack[i] == 0 && !t[i]) y = i;
}
if (y == -1) { // n_l = t
// update label
int alpha = INF;
for (int i = 0; i < n; ++i) { // O(V)
if (!t[i]) {
alpha = min(alpha, slack[i]);
}
}
for (int i = 0; i < n; ++i) { // O(V)
if (s[i]) l_x[i] -= alpha;
if (t[i]) l_y[i] += alpha;
}
for (int i = 0; i < n; ++i) { // O(V)
if (!t[i]) {
slack[i] -= alpha;
if (slack[i] == 0) {
y = i;
}
}
}
}
// n_l != t is guaranteed
if (match_y[y] == -1) { // free
tree_y[y] = slack_x[y];
while (y != -1) {
int x = tree_y[y];
match_y[y] = x;
int next_y = match_x[x];
match_x[x] = y;
y = next_y;
}
m++;
}
else { // matched
int z = match_y[y];
tree_x[z] = y;
tree_y[y] = slack_x[y];
s[z] = 1;
t[y] = 1;
// z가 추가되었으므로 slack과 n_l이 update
for (int i = 0; i < n; ++i) { // O(V)
if (l_x[z] + l_y[i] - w[z][i] < slack[i]) {
slack[i] = l_x[z] + l_y[i] - w[z][i];
slack_x[i] = z;
}
}
goto here;
}
}
for (int i = 0; i < n; ++i) {
ret += l_x[i];
ret += l_y[i];
}
return ret;
}
헝가리안 알고리즘을 사용하여 해결할 수 있는 문제로는 대표적으로 다음과 같은 것이 있습니다.