TAMREF's profile image

TAMREF

April 18, 2021 00:00

Introduction

Childhood

중학교에서 전기 회로에 대해 배울 때를 떠올려 봅시다. “전압 $V$는 전류 $I$와 저항 $R$의 곱과 같다”는 옴의 법칙을 배운 뒤, 저항이 여러 개 연결되어 있을 때, 저항값이 같은 하나의 합성 저항으로 바꾸는 방법을 배웁니다. 바로 직렬 연결과 병렬 연결이죠. ​

• 직렬 연결. 저항 $R _ {1}$과 $R _ {2}$가 직렬로 연결되어 있다면, 합성 저항 $R _ {eq}$는 $R _ {eq} = R _ {1} + R _ {2}$를 만족한다.

• 병렬 연결. 저항 $R _ {1}, R _ {2}$가 병렬로 연결되어 있다면, 합성 저항 $R _ {eq}$는 $\frac{1}{R _ {eq}} = \frac{1}{R _ {1}} + \frac{1}{R _ {2}}$를 만족한다. ​ 이 두 가지 연결 방법만 알고 있다면 세상의 모든 합성 저항을 손쉽게 계산할 수 있을 것만 같습니다. 하지만 그 꿈은, 고등학교 물리나 대학교 일반물리 과목에서 다음과 같은 회로를 만나면서 깨어지게 됩니다. ​

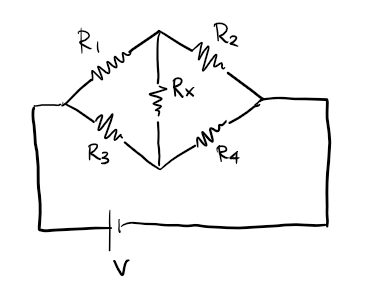
휘트스톤 브릿지 (Wheatstone Bridge)라고 불리는 이 회로에서 합성 저항을 계산하기 위해서는 보다 본질적인 법칙인 키르히호프 법칙을 사용하여 각 저항에 흐르는 전류에 대한 복잡한 연립 방정식을 풀어야 합니다. 그 결과도 $R$들의 복잡한 유리식으로 나타나게 되는데, 일반적으로 “$R _ {x}$에 전류가 흐르지 않을 필요충분조건은 $R _ {1}R _ {4} = R _ {2}R _ {3}$이다”라는 사실을 많이 배웁니다. 언뜻 듣기에 상당한 복잡도를 가진 법칙처럼 보이지만, 사실 그 내용 자체는 법칙이라는 이름이 부끄러울 정도로 간단합니다. ​

Master Solution: Kirchoff’s law

• 키르히호프 1법칙. (전하량 보존 법칙) 한 점에서 들어오고 나가는 전류의 합은 $0$이다.
• 키르히호프 2법칙. (폐회로의 법칙) 임의의 닫힌 회로에 대해서 전압 변화의 합은 $0$이다.

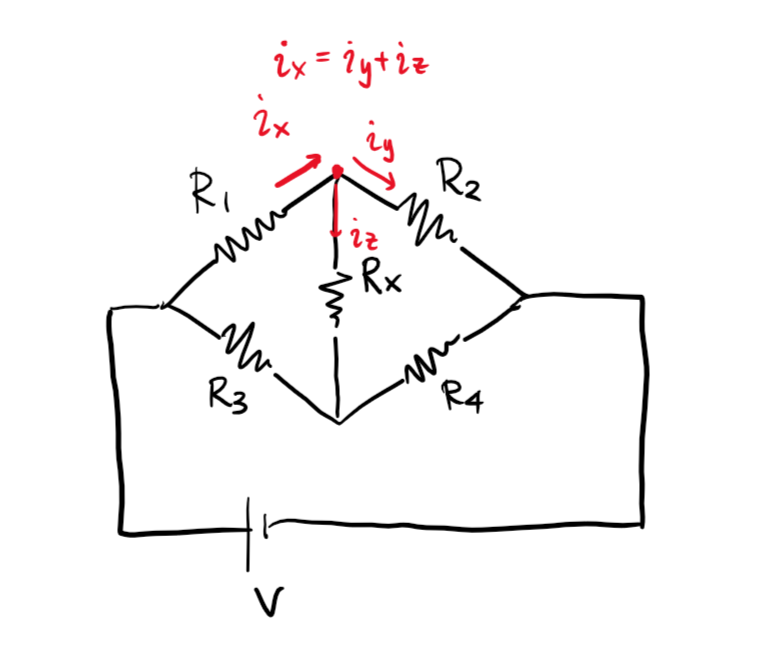
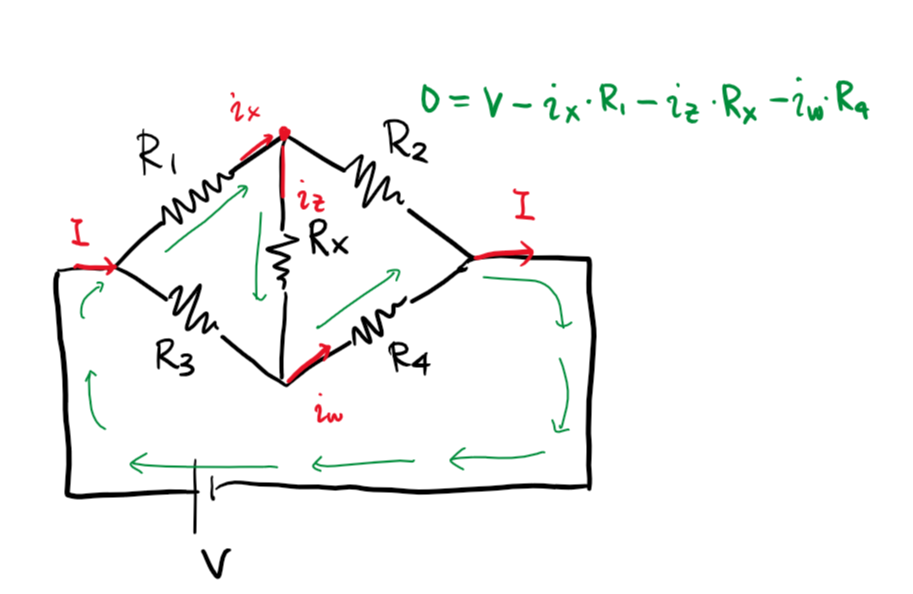
간단하게 이 법칙이 합성 저항 문제를 “풀 수 있는” 이유를 생각해볼 수 있습니다. 회로를 그래프로 생각했을 때, 전류가 모이고 나가는 분기점을 정점, (저항 또는 전원이 있는) 도선을 간선으로 생각해 봅시다. 결국 각 간선에 흐르는 전류의 값을 모두 알 수 있다면 합성 저항은 전압 $V$ / 총 전류 $I$가 되므로 손쉽게 구할 수 있게 됩니다. 정점이 $n$개, 간선이 $m$개라고 하면 총 $m$변수 연립 방정식을 풀어야 하는 셈입니다.

• 1법칙은 총 $n$개의 식을 줍니다. 하지만 이는 $n-1$개의 식과 등가인데, 간단히 말하면 모든 식을 합했을 때 $0 = 0$ 꼴이 되어 자유도가 하나 감소하기 때문입니다.
• 2법칙은 서로 독립인 사이클 개수만큼의 식을 추가로 줍니다. 이는 그래프가 연결되어 있다는 가정 하에 $m - (n - 1)$개가 있습니다. ​ 따라서 두 법칙을 조합하면 총 $m$개의 독립인 방정식을 얻을 수 있습니다. 변수가 $m$개고 식도 $m$개이니 풀 수 있는 방정식입니다. ​ 사실 그래프 이론을 알고 있다면, 이 “전류 방정식”을 풀 수 있는 보다 직관적인 방법을 얻을 수 있습니다. 회로를 그래프로 생각했을 때, 그래프의 스패닝 트리 $T$를 잡습니다. ​
• 스패닝 트리 $T$의 간선에 흐르는 전류들을 $n-1$개의 독립 변수 $j _ {1}, \cdots, j _ {n-1}$로 둡니다.
• $e \notin T$에 대해, $T + e$에 있는 유일한 사이클에 키르히호프 2법칙을 적용합니다. $e$에 흐르는 전류 $i _ {e}$를 $j _ {1}, \cdots, j _ {n-1}$의 선형 결합으로 직접적으로 표현할 수 있습니다. 이제 변수가 $n-1$개인 식이 되었씁니다.
• 이제 $n-1$개의 변수로 키르히호프 1법칙을 적용하여 방정식을 해결하면 됩니다. ​ 기존의 방식을 변주한 것에 불과하지만, 간선들을 “스패닝 트리의 간선들”과 “$T + e$에 있는 유일한 사이클”로 나누어 고려했다는 부분을 기억해 둡시다. 그래프의 스패닝 트리와 합성 저항은 의외로 밀접한 관련이 있습니다. ​

  Back to childhood

기왕 회로를 그래프로 보기로 약속했으니, 이제 휘트스톤 브리지가 어떤 그래프인지 봅시다.

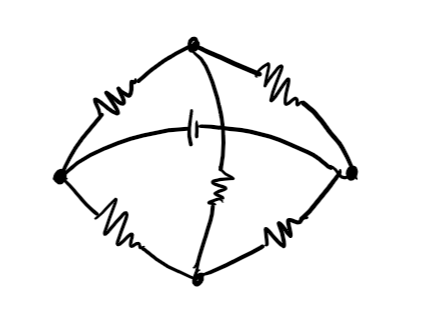
우리가 잘 아는 정점 $4$개짜리 완전그래프, 즉 $K _ {4}$입니다. 그리고 이제 직렬-병렬 연결로 해결할 수 있는 커다란 그래프를 봅시다.

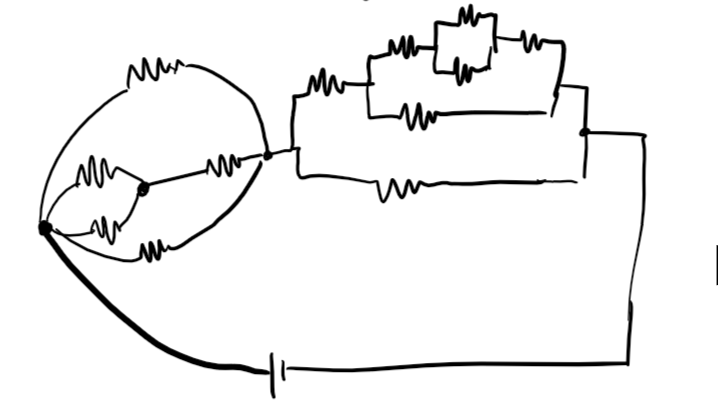
굉장히 크고 복잡하게 생긴 그래프이지만, 어쩐지 풀 수 있을 것 같은 친숙함이 느껴집니다. 그런데 한 가지 주목할 점은, 이 그래프에서는 $K _ {4}$를 찾을 수 없다는 사실입니다. 보다 엄밀하게는, $K _ {4}$처럼 생긴 구조조차도 찾을 수가 없습니다.

여기서 $K _ {4}$처럼 생긴 구조란, $K _ {4}$의 간선을 여러 번 세분 (subdivision)해서 얻을 수 있는 그래프를 말합니다. 아래의 그래프는 $K _ {4}$의 subdivision을 포함합니다.

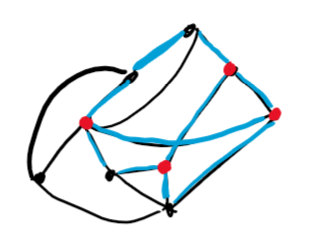
결론부터 말해, 다음의 정리가 성립합니다:

“직렬연결과 병렬 연결을 통해 합성 저항을 구할 수 있는 네트워크의 집합” = “그래프로서 $K _ {4}$의 subdivision을 포함하지 않는 네트워크의 집합” 또, 이러한 그래프들의 집합을 이름 그대로 Series-Parallel Network라고 부릅니다. 즉, 이 결론을 통해 우리는 “Wheatstone bridge가 어려운 이유는 $K _ {4}$이기 때문이고, 이는 Series-Parallel Network에 속하지 않는 minimal한 예시이기 때문이다” 라고 말할 수 있게 되었습니다!

앞으로 전개될 본문에서는 다음의 내용들을 알아봅니다.

• Series-Parallel Graph의 정의와 $K _ {4}$-minor free Graph와의 등가성
• Why Series-Parallel Network?: 전기 회로로써 Series-Parallel Network의 이점
• Beyond Series-Parallel: 일반적인 그래프에서 합성 저항을 구하는 방법
• Addendum: Series-Parallel Graph class에서의 여러 알고리즘 ​

  Series-Parallel Graph

이 단원에서는 그래프의 언어를 벗어나지 않습니다. 저항의 context가 꼭 필요하지 않다는 의미입니다. ​ 두 개 이상의 정점을 갖는 그래프 $G$에 대해 간선이나 정점을 줄이는 두 가지 연산을 정의합니다. ​

• Series Reduction.차수 $2$인 정점을 지우고 간선 하나로 대체한다 – 직렬 연결된 두 저항을 합성 저항으로 대체하는 것과 대응됩니다.
• Parallel Reduction. Multi Edge를 하나로 합쳐준다 – 병렬 연결된 저항들을 합성저항으로 바꾸는 것과 대응됩니다.

이 두 가지 Reduction을 이용해서 그래프를 $K _ {2}$로 바꿀 수 있다면, $G$를 Series-Parallel Graph라고 부릅니다. Series-Parallel Graph에는 항상 $G + st$가 cut-edge free가 되는 서로 다른 두 정점 $s, t$가 존재합니다. Reduction을 통해 남는 두 정점을 선택한 뒤, Reduction의 역과정을 그대로 밟으면 되기 때문입니다.

Reduction과는 반대로, 그래프 $G$와 두 정점 $s \neq t$의 순서쌍 (two-terminal graph) $(G, s, t)$에 대해, 간선이나 정점을 늘릴 수 있는 두 가지 연산을 정의합니다.

• Series Composition. 공유하는 정점이 없는 $(G, s, t)$와 $(H, s^{\prime}, t^{\prime})$에 대해, $t$와 $s\prime$을 한 정점으로 합친 새로운 two-terminal graph $(GH, s, t\prime)$을 만든다.
• Parallel Composition. $s$와 $s\prime$, $t$와 $t\prime$을 각각 한 정점으로 합친 새로운 two-terminal graph $(G \Vert H, (s=s^{\prime}), (t=t^{\prime}))$을 만든다.

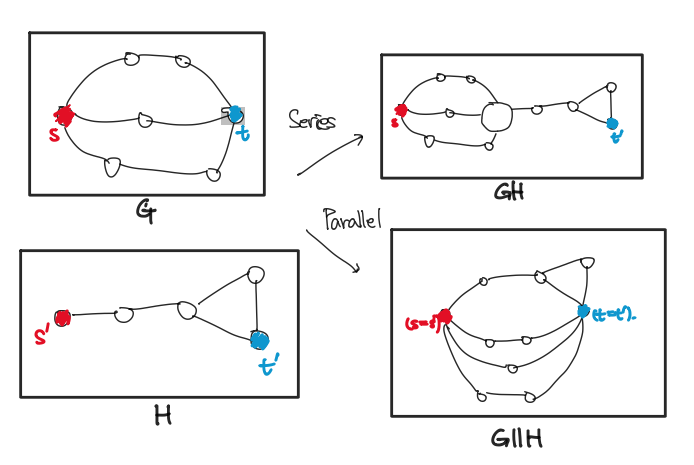
이 때, $K _ {2}$의 two-terminal graph 유한 개로부터 Composition을 유한 번 적용하여 만들 수 있는 그래프의 모임 역시 Series-Parallel Graph가 됩니다.

Series-Parallel Graph는 항상 Confluence라 불리는 좋은 성질을 만족합니다.

Definition. 서로 다른 두 간선 $e$, $f$가 not confluent하다는 것은, $e, f$를 서로 다른 방향으로 통과하는 두 사이클 $C _ {1}, C _ {2}$가 존재한다는 것이다. 그래프 $G$에 not confluent한 $e, f$가 존재하지 않으면 $G$를 confluent graph라고 한다.

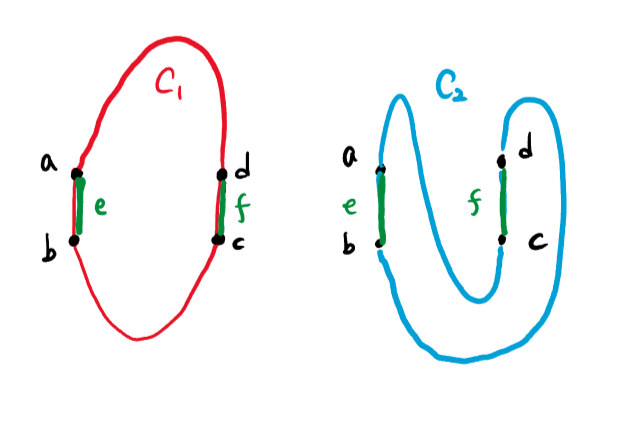
위 그림처럼 두 사이클이 $e, f$를 통과하는 방향이 서로 반대인 사이클 $C _ {1}, C _ {2}$가 있다면 $e, f$는 confluent하지 않습니다. $K _ {4}$의 subdivision을 부분그래프로 갖는 경우 그래프가 confluent하지 않다는 사실을 쉽게 알 수 있습니다.

Theorem (Duffin, 1965). $G$ is series-parallel if and only if $G$ is confluent. $\square$

위 정리는 수학적 귀납법을 이용해서 큰 어려움 없이 증명할 수 있지만, 과정이 다소 번거로운 부분이 있어 생략합니다. Confluence라는 성질로 series-parallel property를 번역하고 나면, 다음의 정리에 다가가기 다소 쉬워집니다.

Theorem. $G$ is confluent if and only if $G$ does not contain subdivision of $K _ {4}$ as subgraph.

Sketch of Proof. $G$가 $K _ {4}$의 subdivision을 가지면 confluent하지 않음은 자명합니다. 이제 $G$가 not confluent하다고 하면 $K _ {4}$의 subdivision을 가진다는 사실을 증명하면 됩니다.

Not confluent한 간선 $e, f$를 서로 다른 방향으로 통과하는 cycle $C _ {1}, C _ {2}$를 잡고, 두 사이클에 속한 간선만 남기도록 합시다. $C _ {1}$을 $e, f$를 통과하는 원으로 보았을 때, $C _ {2}$를 따라가다 보면 $e, f$의 “위쪽 호”에서 출발해서 위쪽 호의 정점을 전혀 만나지 않고 “아래쪽 호”에 도착하는 최초의 경로 $g$가 정의상 존재해야 합니다.

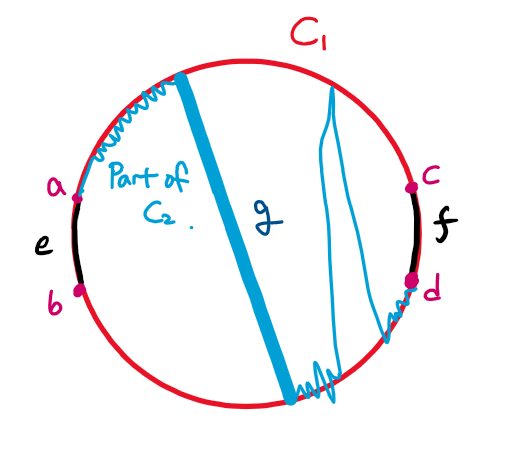
위 그림은 $e$의 한 끝점인 $a$에서 출발하여 $d$에 도착하기까지 $C _ {2}$의 일부분을 파란색 경로로 나타낸 것입니다. 굵은 경로가 $g$를 나타냅니다. 이후 $c$에 도착하여, $g$를 기준으로 “왼쪽 호”에 위치한 $b$에 도착하기 위해서는 역시 $g$를 기준으로 오른쪽 호에서 출발하여 오른쪽 호의 정점을 만나지 않고 왼쪽 호로 도달하는 경로 $h$가 존재해야 합니다.

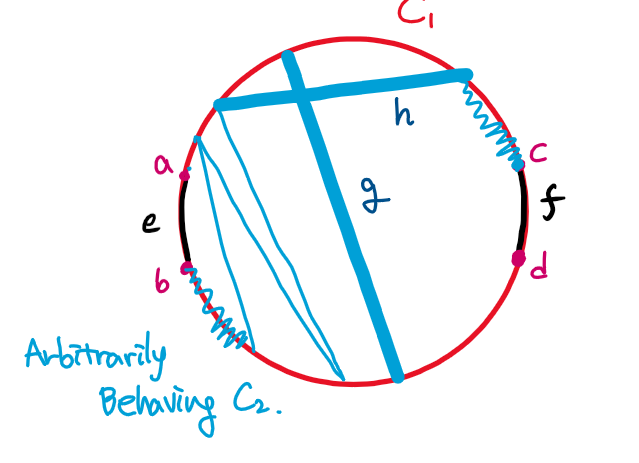
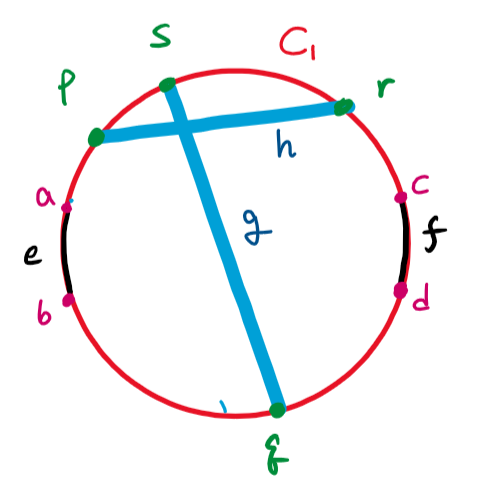
이 때 $g, h$의 양 끝점에 해당하는 정점 $p, q, r, s$는 각각 다르고, (사이클인 $C _ {2}$에 속해있기 때문) $K _ {4}$의 subdivision을 이루는 것을 확인할 수 있습니다. 따라서 $K _ {4}$ subdivision을 포함하는 것과 non-confluency가 동치임을 보일 수 있었고, 최종적으로 series-parallel property가 $K _ {4}$ subdivision avoiding과 동치임을 확인할 수 있습니다.

Series-Parallel Electric Circuit

어떤 전기 회로가 Series-Parallel Graph, 즉 Confluent Graph 구조를 가진다고 합시다. 이런 그래프들만이 갖고 있는 흥미로운 특징 중 하나는, 저항 값이 어떻게 변하더라도 전류가 흐르는 방향이 정해져 있다는 것입니다. 반대로, 어떤 그래프가 non-confluent하다면, 저항 값에 따라서 전류가 흐르는 방향이 바뀔 수 있다는 것을 암시합니다. 당장 Wheatstone bridge가 그 예시로, $R _ {1}R _ {4} = R _ {2}R _ {3}$가 성립하는 평형점을 기준으로 가운데 저항인 $R _ {x}$에 전류가 흐르는 방향이 바뀌는 것을 알 수 있습니다. ​ Confluency를 이용하여 이 사실을 쉽게 보일 수 있습니다. Non-confluent한 두 간선 $a, b$에 대해, $a$에 배터리를 연결하고 $b$에 저항이 있다고 합시다. $a, b$를 서로 반대 방향으로 통과하는 두 사이클 $C _ {1}, C _ {2}$를 생각하면, ​

• $C _ {1}$ 위에 있는 저항만 $1\Omega$이고 나머지는 모두 $\infty$라면, 전류는 $C _ {1}$을 따라 흐르게 됩니다.
• $C _ {2}$ 위에 있는 저항만 빼고 나머지는 모두 저항이 $\infty$라면, 전류는 $C _ {2}$를 따라 흐르게 됩니다. ​ 즉, $b$에 흐르는 전류의 방향이 바뀌게 되는 것을 알 수 있습니다! ​ 반대로 $a$에 배터리를 연결했을 때, 저항값을 잘 골라서 간선 $b$에 흐르는 전류의 방향이 반대인 두 상황을 만들 수 있다고 합시다. 이 때 $b$에 흐르는 전류는 $0$이 아니므로, 키르히호프의 $1$법칙에 따라 $b$의 전압이 낮은 쪽 끝점에서 다른 점으로 흐르는 전류가 있어야 하고, 그 점으로 이동하면서 전압은 감소하게 됩니다. 반대로 $b$의 전압이 더 높은 쪽 끝점으로 전류를 보내주는 곳이 있어야 하고, 그 점으로 이동할 때는 전압이 증가해야 합니다. 결국 전압이 가장 낮고 / 가장 높은 $a$의 양 끝점으로 이동하는 사이클을 찾을 수 있고, 두 상황에서 나오는 사이클은 $a, b$를 서로 다른 방향으로 통과합니다. 따라서 $a, b$는 confluent하지 않습니다! ​ 즉 전지가 연결된 간선 $a$에 대해 $a, b$가 confluent한 것과 $b$의 전류 방향이 바뀌지 않는 것은 동치이고, 이로부터 전자 기기를 직-병렬을 통해서만 연결하면 (그리고 그렇게 연결해야만) 시간에 따라 기기들의 저항이 증가하는 현상이 발생하더라도 전류가 역류하지는 않는다는 사실을 보장할 수 있습니다. :) ​

  General Electric Circuit

그렇다면 wheatstone bridge를 포함하는, 일반적인 Electric Circuit에서 합성 저항은 어떻게 구해야 좋을까요? 여기서는 합성 저항을 계산하는 방법 중 하나인 Graph Laplacian을 소개하고, effective resistance의 조합적 대응을 생각해봅니다.

Discrete Laplace Equation

회로 $G$에 $n$개의 점이 있고, $i$번 점과 $j$번 점을 연결하는 저항 $R _ {ij}$의 도선이 있다고 합시다. 도선이 없는 경우는 $R _ {ij} = \infty$로 자연스럽게 생각할 수 있습니다. 이 때 $a$번 점과 $b$번 점 사이에 전류가 $I$만큼 흐르도록 배터리(전류원)를 연결했다고 합시다. $a$가 고전압, $b$가 저전압입니다. 이전 문단과는 달리 여기서는 배터리를 그래프로부터 떼어 놓고 고려합니다.

키르히호프 제 1법칙과 옴의 법칙으로부터, $n$개의 정점의 전압을 각각 $V _ {1}, \cdots, V _ {n}$이라고 두면 $i$ 번 정점에 대해 다음 식이 성립하게 됩니다.

• $i \neq a, b$인 경우, $\sum _ {j \neq i} \frac{1}{R _ {ij}} (V _ {i} - V _ {j}) = 0$. (들어가고 나가는 전류의 양은 0)
• $i = a$인 경우, $\sum _ {j \neq a} \frac{1}{R _ {aj}} (V _ {a}- V _ {j}) = I$.
• $i = b$인 경우, $\sum _ {j \neq b} \frac{1}{R _ {bj}} (V _ {b}- V _ {j}) = -I$

이 때 $R _ {ij}^{-1}$을 전도율 (conductance) $C _ {ij}$라고 두고, 위 방정식을 정리해봅시다.

• 좌변에서 $V _ {i}$의 계수는 $\sum _ {j \neq i} C _ {ij}$, $i \neq j$에 대해 $V _ {j}$의 계수는 $-C _ {ij}$가 됩니다.
• 이 때 행렬 $L$의 원소 $L _ {ij}$를 $i$번 정점에 대한 $V _ {j}$의 계수로 둡시다. 이 $L$을 $G$의 Laplacian이라고 합니다.
• Net-flow vector $F$의 원소 $F _ {i}$를 $i$번째 식의 우변 (즉, $i$번 점에서 빠져나가는 전류의 총량)으로 둡시다. $F = I(\mathbf{e} _ {a} - \mathbf{e} _ {b})$가 성립합니다.

$V = (V _ {1}, \cdots, V _ {n})^{\mathbf{t}}$로 두면, $LV = F$라는 “discrete laplace equation (DLE)”을 얻게 됩니다. 이 방정식을 만족하는 $V$를 구할 수 있다면, $R _ {eq} = \frac{V _ {a} - V _ {b}}{I}$를 얻을 수 있습니다.

Solving DLE

하지만 $L$이 invertible하지 않기 때문에 바로 $L^{-1}$을 곱할 수는 없습니다. 다만, $G$가 connected라면 (즉, 도선을 통해 모든 점이 이어져 있다면) $L$의 rank가 $n-1$임이 알려져 있습니다. 이는 $G$가 모든 $C _ {ij} \in {0, 1}$인 트리라고 두고 생각해 보면 좋습니다. $G$가 connected가 아닌 경우는 의미가 없으므로, connectedness를 가정하도록 하겠습니다.

$L$의 1차원 kernel은 $\mathrm{span}(1, 1, \cdots, 1)$입니다. 이는 $L$의 한 row의 원소를 다 합하면 $0$이라는 사실로부터 자명하게 유도할 수 있고, 이것이 곧 유일한 kernel이 됩니다. 물리학적으로는 전압의 기준 (0V)을 어떻게 정하더라도 물리 법칙이 바뀌지 않는다는 사실과 맞아떨어집니다.

모든 원소가 $1$인 행렬 $J$를 생각해보면, $L, J$가 모두 대칭행렬이므로 선형대수학 지식으로부터 $L + J$가 invertible하다는 사실을 알 수 있습니다. 이제 $(L + J)^{-1}F$가 DLE의 solution이 될 수 있다는 것을 보이기 위해, $(L + J)V = F$ 를 만족하는 $V$는 $LV = F$ 또한 만족한다는 것을 보이면 됩니다.

$JL = LJ = 0$임을 이용하여 $(L + J)V = F$의 양변에 $J$를 곱합시다. $JF = 0$ 또한 성립하므로, $J^{2}V = 0$을 얻습니다. $J^{2} = nJ$ 가 성립하므로 결국 $JV = 0$을 얻고, 이를 원 식에 대입하면 $LV = F$를 얻습니다.

따라서 $L + J$의 matrix inverse를 계산하면 전체 effective resistance를 계산할 수 있고, 시간 복잡도는 행렬 곱을 하는 시간 정도로, 일반적으로 구현 가능한 범위에서 $O(n^{3})$의 시간이 걸리게 됩니다.

Combinatorial Analogy for Effective Resistance

사실 Graph Laplacian은 Resistance와는 별도로 존재하는 개념으로, 인접행렬로부터바로 정의가 가능합니다.

루프가 없고 (multi-edge는 존재할 수도 있음) connected인 그래프 $G$ 에 대해, 차수 행렬 $D$ 를 $D _ {ii} = \deg (i)$ 인 대각행렬로 정의합시다. $G$의 Laplacian을 $L = D - A$로 정의합니다. 회로에서 Laplacian을 정의했을 때와 매우 유사함을 알 수 있습니다. 회로의 경우와 마찬가지로, $L$의 rank는 $n-1$이 됩니다.

이 때, 다음 정리가 알려져 있습니다:

Theorem. (Matrix-Tree Theorem) $L$의 $0$이 아닌 eigenvalue $\lambda _ {1}, \cdots, \lambda _ {n-1}$에 대해, $G$의 spanning tree의 개수 $k(G)$는 $\frac{1}{n}\lambda _ {1} \cdots \lambda _ {n-1}$과 같다.

Equivalent Descriptions:

• $L$에서 아무 row하나, 아무 column하나를 제거하여 만든 행렬 $\hat{L}$ 에 대해, $\det \hat{L} = k(G)$.
• (Temperley) $\det(L+ J)= n^{2} k(G)$.

이 때, $i$와 $j$를 잇는 multiplicity를 $w _ {ij}$ 라고 하면, spanning tree $T$가 간선 $e _ {1}, \cdots, e _ {n-1}$로 이루어져 있을 때 $k(G) = \sum _ {T : \text{ spanning tree of }G} w _ {e _ 1} \cdots w _ {e _ {n-1}}$이 성립하게 됩니다. 이렇게 두고 보니 $w _ {ij}$가 정수여야 한다는 암묵적인 조건이 전혀 필요하지 않아 보이네요? 실제로 Matrix-Tree Theorem은 $w _ {ij}$가 실수인 상황에서 성립합니다.

$V = (L + J)^{-1}F$에서 Cofactor matrix를 이용하여 계산하면, 다음의 결과 또한 얻을 수 있습니다. 계산 과정이 간단치만은 않으므로 생략합니다.

$ R _ {eq} = \frac{k(G /ij)}{k(G)}$

여기서 $G / ij$란, 두 정점 $i, j$를 잇는 간선을 제거하고 둘을 하나의 정점으로 합쳐서 만든 새로운 그래프를 의미합니다.

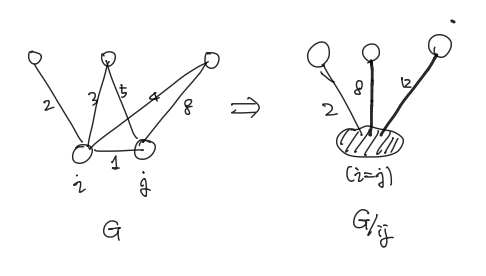
따라서, 회로의 저항을 그래프의 스패닝 트리 개수라는, 자연스러운 조합적 대상으로 환원시킨 셈입니다.

Recall of Series-Parallel Case

간단한 예제로, Series-Parallel Graph의 합성 저항 규칙을 Spanning Tree 개수의 관점에서 새로 유도해봅시다. $(G,s, t)$와 $(H, s\prime, t\prime)$가 주어졌을 때, source와 sink 사이의 저항이 각각 $R(G), R(H)$라면 Composition으로 얻을 수 있는 그래프 $GH, G \Vert H$에 대해 $R(GH) = R(G) + R(H)$와 $R(G \Vert H)^{-1} =R(G)^{-1} + R(H)^{-1}$을 유도해내는 것이 목표입니다.($s^{\prime\prime}, t^{\prime\prime}$은 Parallel Composition에서 합쳐진 정점) 구해야 할 값들은 총 $4$가지가 있겠네요.

• $k(GH)$: $t =s\prime$ 을 기준으로 $GH$의 spanning tree를 쪼개면, 쪼개진 부분은 각각 $G$의 spanning tree와 $H$의 spanning tree에 대응됩니다. 따라서 $k(GH) = k(G)k(H)$.
• $k(GH / st\prime)$: $GH / st\prime$는 결국 $(G, s, t)$와 $(H, t\prime, s\prime)$의 Parallel Composition과 같습니다. 따라서 $k(G \Vert H)$와 같게 됩니다.
• $k(G \Vert H)$: $G \Vert H$의 한 스패닝 트리 $T$에서 $s^{\prime\prime}, t^{\prime\prime}$을 잇는 경로를 생각합시다. $G \Vert H$의 특성 상 이 경로는 $G$에 완전히 속하거나 $H$에 완전히 속합니다. 일반성을 잃지 않고 $G$에 속한다고 해 봅시다. $T$의 간선 중 $G$에 속한 쪽은 $G$의 스패닝 트리가 되고, $H$에 속한 쪽은 $H / st$의 스패닝 트리에 대응되는 것을 알 수 있습니다. 따라서, $s^{\prime\prime},t^{\prime\prime}$을 잇는 경로가 $G$에 속하는 $G \Vert H$의 스패닝 트리는 $k(G)k(H / st)$개 입니다. 반대로도 생각하면 $k(G \Vert H) = k(G)k(H / st) + k(H) k(G / st)$.
• $k(G \Vert H / s^{\prime\prime}t^{\prime\prime})$: $(s’’ =t’’)$이 cut vertex가 됩니다. 곧 $k(G / st) k(H / s’t’)$이 됩니다.

이 값들을 이용하여 합성된 그래프들의 스패닝 트리 개수를 구해보면,

• Series Composition:

  $R(GH) = \frac{k(GH / st’)}{k(GH)} = \frac{k(G)k(H / st) + k(H)k(G/ st)}{k(G)k(H)} = \frac{k(H/st)}{k(H)} + \frac{k(G/st)}{k(G)} = R(G) + R(H)$.

• Parallel Composition: $R(G \Vert H)^{-1} = \frac{k(G \Vert H)}{k(G \Vert H / st)}=\frac{k(G)k(H / st)+k(H)k(G/st)}{k(G/st)k(H/st)}= R(G)^{-1} + R(H)^{-1}$.

우리가 알고 있는 결과가 멋지게 유도됩니다. 이 아이디어를 이용하여 해결할 수 있는 문제로 BOJ 19838 Circuit 이 있습니다.

Theoretical Properties Of Series-Parallel Graph

부록의 느낌으로 “직렬 연결”, “병렬 연결” 이라는 Resistor Network와의 유사성 이외에 Series-Parallel Graph가 가지고 있는 Graph-theory 또는 Algorithmic Benefit에 대해 간단히 알아봅시다.

As a Graph Class

• Series-Parallel Graph는 $K _ {4}$를 포함하지 않습니다. 이 때 $K _ {4}$의 subdivision을 $K _ {5}, K _ {3,3}$에서 찾을 수 있으므로 Series-Parallel Graph는 평면그래프입니다.
• $K _ {2,3}$이 Series-Parallel이므로 Outerplanar는 아닙니다. 반대로 Outerplanar이면 Series-Parallel입니다.
• 정점이 $n$개인 Simple Series-Parallel Graph의 간선 개수는 최대 $2n-3$개로, 삼각형을 이어붙인 그래프가 실례가 됩니다.

Algorithmic Benefit

• (Tarjan, 1982) 어떤 Graph가 Series-Parallel인지 Linear-time에 판정할 수 있습니다.
• (Takamizawa, 1982) 유한 개의 forbidden minor / forbidden topological minor로 characterize되는 Graph property $Q$의 경우, 다음 문제들을 linear time에 해결할 수있습니다.
  • $Q$-decision problem.
  • Minimum Vertex Deletion / Edge Deletion to achieve $Q$.
    • Feedback Vertex Set: 그래프가 acyclic해지기 위해 제거해야 하는 간선의 최소 개수
    • Maximum Induced Line Subgraph
• (Takamizawa, 1982) 적당한 그래프 $B$에 대해, 그래프 안에 Vertex-disjoint한 $B$를 최대 몇 개 넣을 수 있는지 linear time에 알 수 있습니다.
  • Maximum Matching Problem: $B = K _ {2}$.
  • Maximum Disjoint Triangle Problem: $B = K _ {3}$.
• (Takamizawa, 1982) 이외에, linear time에 maximum cycle problem (hamiltonian cycle problem), maximum path problem 등을 해결할 수 있습니다. 이는 Series-Parallel Graph의 “divide-and-conquer” 스러운 특성과 연관되어 있습니다.