Stoer-Wagner Algorithm
안녕하세요?
오늘은 Stoer-Wagner 알고리즘에 대해 살펴보겠습니다.
Stoer-Wanger 알고리즘은 그래프의 Global Minimum Cut을 찾는 알고리즘입니다.
Introduction
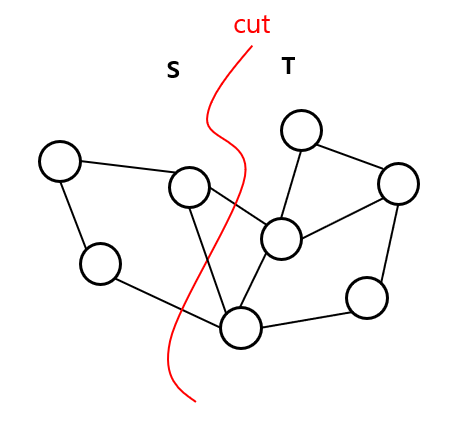
그래프를 두 집합 $S$, $T$로 나누는 것을 그래프의 cut이라고 합니다. 간선에 weight가 있는 그래프에서, 두 점 $s$와 $t$가 주어졌을 때 $s \in S$, $t \in T$를 만족하도록 그래프를 cut하는 상황을 생각해봅시다.
한 쪽 노드는 집합 $S$에, 다른 한 쪽은 $T$에 포함된 모든 edge들의 weight의 합을 cut의 크기라고 합니다. 이 때 크기가 가장 작은 최소 cut은 최대 유량과 같다는 사실(Min-cut Max-flow theorem)은 잘 알려져 있습니다.
따라서 최대 유량을 구하는 여러 알고리즘(Edmond-Karp algorithm, Dinic algorithm 등)을 적용하여, 최소 컷의 크기를 쉽게 구할 수 있습니다.
하지만 두 점 $s$와 $t$가 정해지지 않은, 전체 그래프에서의 global minimum cut을 찾는 것은 어떨까요? 이를 찾는 대표적인 알고리즘으로 deterministic한 Stoer-Wagner Algorithm, 그리고 randomize algorithm인 Karger’s Algorithm이 있습니다.
이번 글에서는 그 중에서 Stoer-Wagner algorithm을 소개하도록 하겠습니다.
제가 예전에 소개드렸던 Karger’s Algorithm도 함께 알아두시면 더욱 흥미롭게 느끼실 수 있으시리라 생각합니다.
Stoer-Wagner Algorithm
Stoer-Wagner 알고리즘은 매우 간단한 원리를 기반으로 동작합니다.
global min cut $C$가 있을 때, 임의의 두 점 $s$, $t$에 대해, $s$와 $t$는 $C$에 대해 다른 side에 존재하거나, 같은 side에 존재하는 두 가지 경우만이 존재합니다. 너무 당연한 말입니다.
그렇다면 이 성질을 어떻게 이용할 수 있을까요?
만약 우리가 어떠한 두 점 $s$, $t$ 사이의 min cut을 알 수 있다면,
- $s$, $t$가 $C$에 대해 다른 side에 존재할 경우: 이 경우 $s$, $t$ 사이의 min cut이 global min cut이 됩니다
- $s$, $t$가 $C$에 대해 같은 side에 존재할 경우: $s$와 $t$를 서로 합쳐주어도(Edge contraction) global min cut은 변하지 않게 됩니다. 이 때 전체 vertex의 수가 하나 감소하는 효과를 보일 수 있습니다.
결국 우리가 해야 할 것은, 어떠한 두 점 $s$, $t$ 사이의 min cut을 구한 뒤, 1번 경우일 수 있으므로 해당 결과를 계속 min 연산하고, 동시에 $s$와 $t$를 merge해주며 vertex가 하나 남을 때까지 계속 진행해주면 된다는 사실을 알 수 있습니다.
그렇다면 알고리즘의 핵심은 어떠한 두 점 $s$, $t$ 사이의 min cut을 최대한 빨리 알아내는 것입니다.
MinimumCutPhase
만약 점 $s$, $t$가 정해져있다면 해당 두 점 사이의 min cut은 Edmond-Karp algorithm, Dinic algorithm 등을 이용해 구할 수 있으며, 이 중 더 빠른 Dinic algorithm의 경우도 $O(V^2E)$의 시간복잡도를 가지지만 우리에게는 조금 더 빠른 방법이 필요합니다.
사실 우리는 두 점이 확실히 정해졌을 때의 min cut을 알 필요 없이, 아무런 두 점에 대해서나 해당 두 점 사이의 min cut을 알기만 하면 되기 때문에 훨씬 더 간단한 문제로 보입니다.
이렇게 어떠한 두 점 사이의 min cut을 찾는 과정을 MinimumCutPhase라고 하겠습니다.
Stoer-Wagner 알고리즘에서 MinimumCutPhase 알고리즘은 다음과 같이 진행됩니다.
- 그래프에서 임의의 node 하나를 고릅니다. 골라진 node들의 집합을 S라 하겠습니다.
- S와 가장 tight하게 연결된 node를 찾아, 해당 node를 S에 추가합니다. 여기서 S에 속하지 않은 점 $v$의 tightness는 $tight(v) = \sum_{u \in S}{w(u,v)}$와 같이 정의됩니다.
- 1번과 2번을 계속 반복하였을 때, 가장 마지막에 추가된 두 개의 node를 $s$, $t$라 하였을 때 $s$, $t$ 사이의 min cut은 $tight(t)$입니다.
아래의 그림은 MinimumCutPhase 알고리즘의 동작 과정을 나타낸 그림입니다.
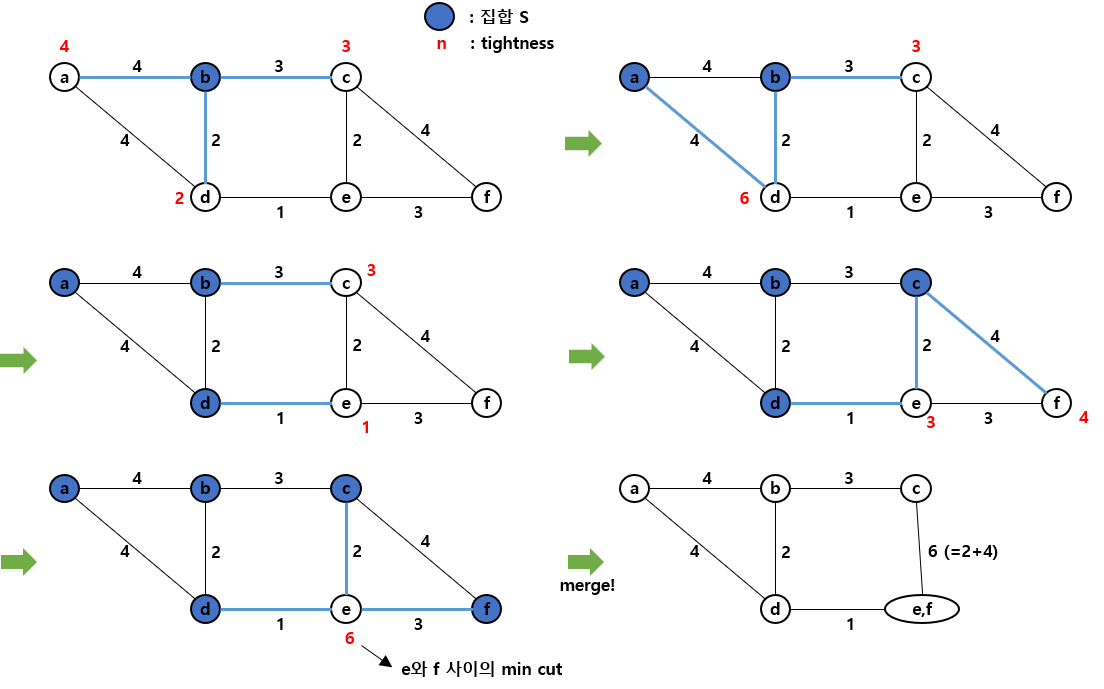
알고리즘은 매우 간단합니다. 이제 이를 증명해보도록 하겠습니다.
증명
우리는 MinimumCutPhase 알고리즘의 진행에 따라 가장 마지막으로 추가되는 두 노드 $s$, $t$에 대해, $s$, $t$를 다른 쪽으로 나누는 임의의 cut $C$는 MinimumCutPhase에서 마지막으로 계산된 값만큼 heavy하다는 것을 보일 것입니다.
증명에 앞서 몇 가지 간단한 정의가 필요합니다.
어떠한 s-t-cut $C$에 대해, MinimumCutPhase 알고리즘에 의해 집합 S에 추가된 순서대로 노드를 나열했을 때, 직전 노드와 C에 대해 반대편에 놓이게 되는 노드들을 active node라고 부르겠습니다. $C$는 s-t-cut이므로 따라 맨 마지막에 나열된 node $t$는 무조건 active node입니다.
어떠한 active node $v$에 대해, $v$ 이전에 추가된 모든 노드들을 $A_v$라고 하며, $A_v \cup {v}$를 cut C와 동일하게 자르는 cut을 $C_v$라 하겠습니다. $C_v$의 weight를 $w(C_v)$라 하겠습니다. 자세한 사항은 아래 그림을 보면 이해하기 쉬우실 것이라 생각합니다.
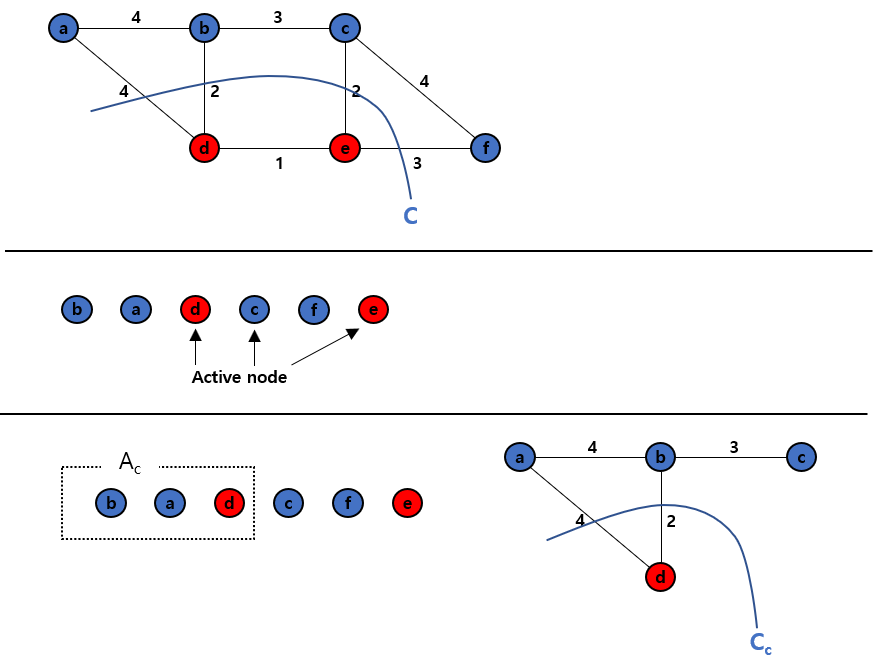
우리는 귀납법을 통해 $w(A_v, v) \le w(C_v)$임을 보일 것입니다.
먼저 가장 첫번째 active node의 경우, $w(A_v, v) = w(C_v)$이므로 성립합니다.
이제 어떠한 active node $u$에 대해, 이전 active node들에 대해 모두 위 식이 성립한다고 할 때 $u$에 대해서도 식이 성립하는 것을 보이면 됩니다. $u$ 직전의 active node를 $v$라고 하겠습니다.
먼저, 당연하게도 $w(A_u, u) = w(A_v, u) + w(A_u - A_v, u)$가 성립합니다.
또, $w(A_v, u) \le w(A_v, v)$가 성립함을 알 수 있는데, 왜냐하면 우리가 수행한 MinimumCutPhase 알고리즘은 항상 가장 tight한 node를 선택했기 때문에 $w(A_v, u) > w(A_v, v)$라면 $v$가 먼저 선택될 수 없습니다.
그리고 $w(C_v) + w(A_u - A_v, u) = W(c_u)$임을 알 수 있는데, $A_u - A_v$, 즉 $v$에서 $u$가 추가되기 전까지의 모든 node들은 $u$와 cut $C$에 대해 다른 방향에 놓이기 때문입니다.
마지막으로 귀납법의 가정에 따라 $w(A_v, v) \le w(C_v)$가 성립합니다.
이제 각 식을 연립하면 완성됩니다.
$w(A_u, u) = w(A_v, u) + w(A_u - A_v, u)$
$\le w(A_v, v) + w(A_u - A_v, u)$
$\le w(C_v) + w(A_u - A_v, u) = W(c_u)$
따라서 모든 active node $v$에 대해 $w(A_v, v) \le w(C_v)$가 성립하며, 이 식은 가장 마지막에 추가된 노드 $t$에 대해서도 성립합니다. 따라서 어떠한 $w(A_t, t) \le w(C)$이며 $w(A_t, t)$는 MinimumCutPhase 알고리즘을 통해서 계산된 값이므로 모든 cut은 해당 값보다 같거나 크다는, 즉 계산된 값이 min cut임을 증명하였습니다.
시간 복잡도
다음으로 알고리즘의 시간 복잡도를 확인해보도록 하겠습니다.
그래프의 node가 $V$개, edge가 $E$개 있다고 가정하겠습니다.
우리는 MinimumCutPhase를 총 $V - 1$회 반복해야 합니다.
그렇다면 한 번의 MinimumCutPhase를 수행하는 시간 복잡도는 얼마일까요?
MinimumCutPhase에서 핵심이 되는 작업인, 집합 S와 가장 tight하게 연결된 node를 찾아, 해당 node를 집합 S에 추가하는 작업을 살펴보겠습니다.
집합 S와 가장 tight하게 연결된 node를 찾는 작업은 마치 MST를 구할 때의 프림 알고리즘처럼 heap을 사용하고 싶게 생겼습니다. 하지만, 뒷부분인 해당 node를 집합 S에 추가하는 작업을 진행할 시 heap 안에 들어있는 값들이 다시 업데이트가 됩니다. 따라서 heap은 사용할 수 없습니다.
가장 단순한 구현방법으로는, 모든 node들을 다 탐방하며 tightness를 업데이트하고, 가장 tight하게 연결된 node를 찾는 방법이 있습니다. 이 경우 추가할 node를 한 번 찾는 데 $O(V)$의 시간이 걸리고, node를 총 $V - 1$번 찾아야 하므로 전체 알고리즘의 시간 복잡도는 $O(V^3)$이 됩니다.
원본 논문에서는 피보나치 힙을 사용하는 것을 제안하였습니다. 피보나치 힙의 경우 max heap에서 increase key라는 연산은 $O(1)$에 진행할 수 있으므로, 어떠한 노드 $v$를 집합 S에 추가할 때
(i) $v$를 피보나치 힙에서 빼내는 연산
(ii) $v$와 연결되었으며, 집합 S에 속하지 않는 노드들의 값을 업데이트
위 두 가지 작업을 진행해야 합니다. 피보나치 힙에서 (i)번 연산은 $O(\log{V})$, (ii)번 연산은 $O(1)$에 수행되며 각각 연산의 수행 횟수는 V번, E번이므로 한 번의 MinimumCutPhase를 수행하는 시간은 $O(V\log{V} + E)$가 됩니다. 따라서 피보나치 힙을 사용하면 전체 시간 복잡도를 $O(V^2\log{V} + VE)$로 제한할 수 있습니다.
제가 생각한 구현 방법으로는, 또다른 자료구조를 만들어 큐에서 업데이트된 원소를 lazy하게 삭제하는 방법도 가능할 것으로 보입니다. 이 경우 한 번의 MinimumCutPhase를 수행하는 데 $O((V+E)\log{(E)})$의 시간이 수행됩니다.
구현
아래는 $O(V^3)$의 방법으로 stoer-wagner 알고리즘을 구현한 코드입니다.
#include <memory.h>
#define N 500
#define INF 987654321
int n;
int w[N][N];
bool merged[N];
bool A[N];
int q[N];
int update_weight(int v) { // update value and return max vertex
int qmax = -1, maxind;
for (int i = 0; i < n; ++i) {
if (!merged[i] && !A[i]) {
q[i] += w[v][i];
if (q[i] > qmax) {
qmax = q[i];
maxind = i;
}
}
}
return maxind;
}
int stoer_wagner() {
int ans = INF;
memset(merged, 0, sizeof(merged));
for (int epoch = 1; epoch < n; ++epoch) {
memset(A, 0, sizeof(A));
memset(q, 0, sizeof(q));
int next, prev;
for (int i = 0; i < n; ++i) {
if (!merged[i]) {
A[i] = 1;
prev = i;
next = update_weight(i);
break;
}
}
for (int i = 0; i < n - epoch - 1; ++i) {
prev = next;
A[next] = 1;
next = update_weight(next);
}
ans = min(ans, q[next]);
merged[next] = 1;
for (int i = 0; i < n; ++i) {
w[i][prev] += w[i][next];
w[prev][i] += w[next][i];
}
}
return ans;
}
마치며
Stoer-Wagner algorithm은 Edge contraction을 진행한다는 점에서 Global min cut을 찾는 또다른 알고리즘인 Karger’s Algorithm과 꽤 유사한 형태를 보입니다.
이러한 Edge contraction 자체는 그래프에 관련된 여러 문제들을 푸는 데 좋은 아이디어로 작용할 수 있을 것 같습니다.
이상 글을 마치겠습니다. 감사합니다.