Zero-Knowledge from MPC
1. Introduction
드디어 Zero-Knowledge에 도달했습니다. 암호학에 그다지 관심이 없었다고 하더라도 최근 Zero-Knowledge가 모네로, 지캐시와 같은 프라이버시 코인에 쓰임으로 인해 Zero-Knowledge라는 단어 혹은 간단한 개념 정도는 익숙한 분이 그럭저럭 있을 것으로 보입니다.
맨 처음에는 게시글 하나를 할애해 Zero-Knowledge에 대한 설명을 하려고 했으나 evenharder님이 작성하신 대화형 증명 시스템과 영지식 증명에 설명이 잘 되어있어서 자세한 설명은 저 글로 대신하고 간단한 요약만 작성하겠습니다.
먼저 $\text{SHA256}(x) = 0^{256}$을 만족하는 $x$를 증명자가 알고 있고, 알고 있다는 사실을 검증자에게 증명하면서도 $x$ 자체는 노출하고 싶지는 않은 상황을 생각해봅시다.
이것이 가능하긴 한건지 의아할 수 있지만 이전 글들에서 우리는 Garbled Circuit을 이용한 Multi-Party Computation을 배웠기 때문에 Garbled Circuit 과정을 잘 생각해보면 위와 같은 증명을 해낼 수 있습니다.
검증자는 Garbler 역할을 맡아 SHA256의 회로와 값들을 선정한 후 증명자에게 보냅니다. 증명자는 Evaluator 역할을 맡아 SHA256을 계산해서 검증자에게 자신이 $\text{SHA256}(x) = 0^{256}$을 만족하는 $x$를 알고 있음을 보일 수 있습니다. Oblivious Transfer의 특성상 Garbler는 Evaluator의 입력을 알 수 없기 때문에 영지식성이 잘 성립합니다.
이와 같이 Zero-Knowledge Proof은 증명자(Prover)가 어떤 명제가 참임을 검증자(Verifier)에게 증명하는데 검증자는 이외의 추가적인 정보를 알 수 없는 증명을 의미합니다.
Zero-Knowledge Proof은 아래의 3가지 성질을 만족해야 합니다.
-
완전성(Completeness) : 증명자가 어떤 명제를 알고 있을 경우 검증자는 증명을 받아들일 수 있어야 합니다.
-
건전성(Soundness) : 증명자가 어떤 명제를 모르고 있을 경우 검증자는 증명을 거절해야 합니다(단, 여러 번 반복을 할 수 있기 때문에 100% 증명을 거절할 수 있어야 할 필요는 없고 negligable하지 않은 확률로 거절을 할 수 있으면 됩니다).
-
영지식성(Zero-Knowledge) : 검증자는 증명으로부터 그 어떤 추가적인 정보도 알 수 없습니다.
Zero-Knowledge Proof을 만드는 방법에는 MPC를 이용하는 방법, 공개키 암호를 이용하는 방법 등이 있지만 이번 글에서는 MPC를 이용한 방법을 같이 살펴보겠습니다.
2. ZK in Graph 3-coloring
사실 이 Zero-Knowledge의 개념은 처음 이렇게 글로만 접하면 이해에 어려움이 많은 개념입니다(적어도 저는 그랬습니다). 인터넷에서 Zero-Knowledge Proof를 검색해보면 알리바바의 동굴 혹은 월리를 찾아라! 로 비유를 해놓은 것을 볼 수 있고 그런 것들을 통해 Zero-Knowledge Proof이 무엇인지는 대략적으로 이해했지만 본격적인 이론으로 들어가면 이해에 어려운 부분이 여럿 있었습니다.
그래서 본격적인 내용에 들어가기 앞서 알리바바의 동굴보다는 조금 더 이론적인 예시를 들어서 설명하겠습니다.
Graph 3-coloring은 주어진 그래프를 3가지의 색깔만 이용해서 정점을 칠하는 문제입니다. 이 때 간선으로 연결된 두 정점은 서로 다른 색으로 칠해져야 합니다. 아래는 3-coloring을 수행한 예시입니다.
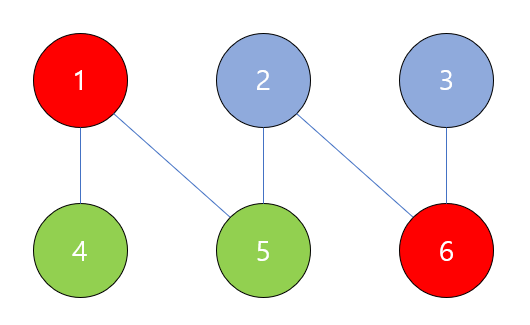
지금 예시로 드는 설명에서 필요한 내용은 아니지만 3-coloring 문제가 NP-complete임은 널리 알려진 사실입니다.
증명자가 자신이 주어진 그래프의 3-coloring을 알고 있음을 검증자에게 증명하면서도 동시에 3-coloring을 하는 방법 자체는 검증자에게 공개하고 싶지 않습니다. 이것을 가능하게 하는 방법은 아래와 같은 방법입니다.
- 증명자는 주어진 그래프를 3-coloring합니다. 이 때 색깔은 매번 랜덤으로 정해야 합니다.
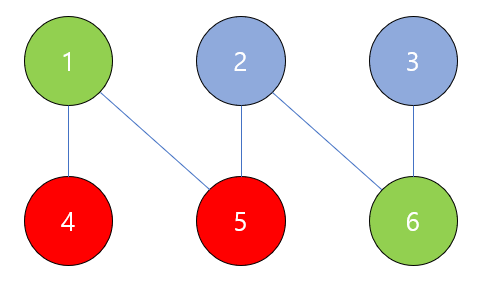
- 증명자는 각 정점의 색깔을 검증자에게 commit합니다(commit : 어떤 값을 약속하고 추후 공개하는 scheme, 선택한 값은 추후에 변경이 불가능함. 해시 함수를 이용해 구현 가능). 검증자는 commit 값만 받았을 뿐 색깔은 알지 못합니다.
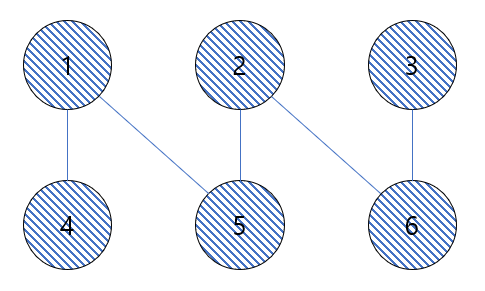
- 검증자는 하나의 간선을 정해서 증명자에게 질문을 합니다.
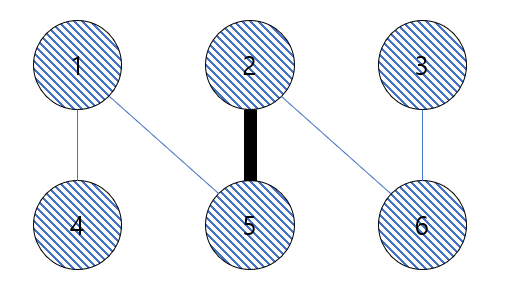
- 증명자는 받은 간선의 두 색깔 정보를 공개합니다. 두 색깔이 일치할 경우 증명자가 3-coloring을 알지 못한다고 판단하고, 일치하지 않을 경우 3-coloring을 안다고 판단합니다.
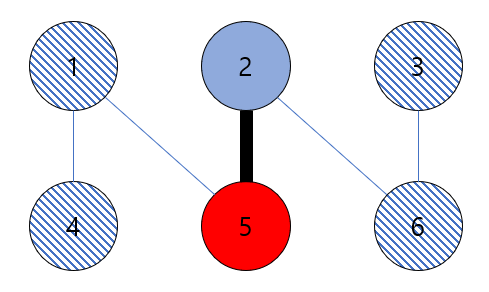
- 위의 과정을 여러 번에 걸쳐 반복합니다.
이 방법이 Zero-Knowledge Proof의 성질을 잘 만족하는지 알아보겠습니다.
-
완전성(Completeness) : 증명자가 3-coloring을 하는 방법을 알고 있다면 검증자는 반드시 증명을 받아들입니다.
-
건전성(Soundness) : 증명자가 3-coloring을 하는 방법을 알고 있지 않다면 최대 $n(n-1)/2$개의 간선 중에서 어느 하나는 두 개의 색이 동일합니다. 그렇기 때문에 이 절차를 한 번 수행할 때 마다 검증자는 적어도 $2 / n(n-1)$의 확률로 증명자가 3-coloring을 하는 방법을 알고 있지 않다는 것을 알 수 있습니다. 검증자가 원하는 확률에 따라 반복 횟수를 정해 Soundness error(증명자가 3-coloring을 하는 방법을 알지 못함에도 불구하고 검증자가 증명을 받아들이는 오류)를 $2^{-80}$ 혹은 $2^{-160}$이하와 같이 정할 수 있습니다.
-
영지식성(Zero-Knowledge) : 검증자는 각 절차마다 2개 정점의 색을 알 수 있습니다. 그러나 이 2개의 색만으로는 3-coloring에 대한 아무런 의미있는 정보를 알 수 없습니다.
아무런 의미있는 정보를 알 수 없다를 수학적으로 정의하려면 더 복잡하지만 관련된 얘기는 생략하겠습니다.
이와 같이 Zero-Knowledge Proof의 3가지 성질이 잘 만족됨을 확인할 수 있습니다. 이 예시를 통해 Zero-Knowledge를 이해하는데에 도움이 되었으면 좋겠습니다.
3. MPC-in-the-head
위의 예시를 통해 우리는 Graph 3-Coloring 문제를 Zero-Knowledge Proof하는 방법을 익혔습니다. 여기서 더 나아가 임의의 일방향 함수 $f$에 대해 $f(x) = y$를 만족하는 $x$를 알고 있음을 Zero-Knowledge Proof하는 방법에 대해 고민해보겠습니다. 참고로 이 방법은 Picnic이라는 이름의 Post-Quantum Digital Signature 알고리즘에서 활용이 됩니다. Picnic에 대해서는 다음 글에서 작성을 할 계획입니다.
Introduction에서 Garbled Circuit을 이용한 Zero-Knowledge Proof를 간단하게 제시했지만 실제 MPC를 이용한 Zero-Knowledge Proof에서는 보다 더 효율적인 방법을 사용합니다. 이를 알기 위해서는 MPC-in-the-head라는 개념을 이해해야 합니다.
MPC-in-the-head는 원래는 Multi-Party가 참여하는 MPC를 혼자서 하는, 말 그대로 MPC를 혼자 머릿속에서(in the head) 수행하는 것을 의미합니다.
원래 MPC는 $N$명이 각각 입력 $w_1, w_2, \dots, w_n$을 가지고 $f(w_1, w_2, \dots , w_n)$를 안전하게 계산하는 프로토콜입니다. MPC-in-the-head에서는 증명자가 $h(w) = y$를 만족하는 $w$를 알고 있음을 증명하고 싶을 때 먼저 $w_1 \oplus w_2 \oplus \dots \oplus w_n = w$을 임의로 정합니다. 이를 일종의 Secret Sharing이라고 생각해도 무방합니다. 그 후 $f(w_1, w_2, \dots , w_n) = h(w_1 \oplus w_2 \oplus \dots \oplus w_n)$을 직접 MPC를 수행해서 계산하면 됩니다.
그렇다면 검증자는 이 과정에서 어떤 역할을 맡아서 검증을 수행할까요? 절차는 Graph 3-coloring에서의 절차와 비슷합니다. 증명자의 머릿속에서 MPC를 수행하는 가상의 $n$명의 사용자를 생각해봅시다. 이들은 MPC를 진행하면서 서로 주고 받는 정보가 있습니다. MPC는 각 사용자 사이의 비밀 통신 채널이 있다는 것을 전제로 하기 때문에 두 사용자가 주고 받은 정보는 그들에게만 보입니다.
-
증명자는 각 사용자의 관점에서 주고 받은 정보를 전부 commit합니다. 마치 그래프의 예시에서 정점의 색을 commit하는 것과 동일한 상황입니다.
-
검증자는 $n$명의 사용자 중에서 2명 $i, j$를 정해 이 둘의 정보를 공개할 것을 증명자에게 요구합니다.
-
증명자는 그 2명의 정보를 검증자에게 줍니다.
-
검증자는 정보를 받아 commit에 문제가 없는지, $i$가 $j$에게 보낸 정보와 $j$가 $i$에게 받은 정보가 일치하는지, $j$가 $i$에게 보낸 정보와 $i$가 $j$에게 받은 정보가 일치하는지 등을 확인해 문제가 없는 경우 증명자가 $h(w) = y$를 만족하는 $w$를 알고 있음을 받아들이고 그렇지 않을 경우 거절합니다.
완전성, 건전성, 영지식성은 위와 비슷하게 표현할 수 있기 때문에 생략하겠습니다. MPC-in-the-head를 그림으로 나타내면 아래와 같습니다.
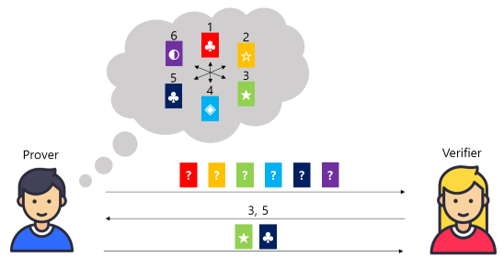
처음 MPC를 이용해 Zero-Knowledge Proof을 하는 방법이 소개된 논문(Yuval Ishai, Eyal Kushilevitz, Rafail Ostrovsky, and Amit Sahai. 2007. Zero-knowledge from secure multiparty computation.)에서는 완전성, 건전성, 영지식성을 수학적인 표현으로 정의하고 이외에도 Robustness, Privacy, Correctness 등의 다양한 개념들이 소개되지만 이번 글에서는 너무 이론적으로 깊게 들어가는 대신 동작 방식을 대략적으로 받아들일 수 있을 정도로만 설명하고 넘어가겠습니다.
4. Fiat-Shamir Transform
MPC-in-the-head를 통해 interactive한 Zero-Knowledge Proof을 만들 수 있습니다. 각 계산마다 증명자가 검증자에게 commit을 보내는 통신, 증명자가 검증자에게 요구할 2명의 정보를 보내는 통신, 검증자가 증명자에게 정보를 돌려주는 통신 총 3번의 통신을 필요로 합니다.
한편 Fiat-Shamir Transform은 Zero-Knowledge Proof를 Non-Interactive Zero-Knowledge Proof로 변환해줍니다. Fiat-Shamir Transform을 줄여서 FS라고 쓰기도 하고, Non-Interactive Zero-Knowledge를 줄여서 NIZK로 쓰기도 합니다. 이 변환은 1987년 처음 제시되었고(Amos Fiat and Adi Shamir. 1987. How to prove yourself: practical solutions to identification and signature problems.) 수학적으로 안전함이 증명되어있습니다.
Fat-Shamir Transform은 Non-Interactive Zero-Knowledge이라는 이름에서 볼 수 있듯 증명자와 검증자가 3번의 통신을 거쳐 증명을 완료하는 대신 증명자가 검증자에게 일방향으로 정보를 보내고 검증자는 이를 보고 증명을 받아들일 수 있습니다.
Fiat-Shamir Transform에 쓰이는 아이디어는 그렇게 어렵지 않습니다. 검증자가 $i, j$를 보내는 이유는 증명자가 정할 수 없는 두 사용자를 선택하기 위함이기 때문입니다. 반대로 말하면 검증자로부터 $i, j$를 받는 대신 검증자도 납득할 수 있는 방법으로 $i, j$를 증명자가 생성할수만 있다면 Interactive한 과정을 Non-Interactive하게 바꿉니다. 우선 아래의 변환 과정을 먼저 보겠습니다.
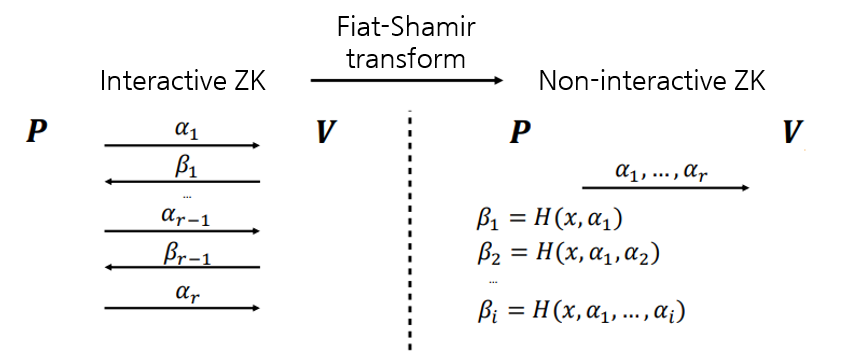
Transform을 보면 Interactive ZK에서는 검증자(V)로부터 받아야 하는 값 $\beta_1, \dots , \beta_{r-1}$을 Non-interactive ZK에서는 해시 함수의 값으로부터 얻어냅니다. 이 절차를 통해 검증자는 $\beta_1, \dots , \beta_{r-1}$가 랜덤하게 생성되었음을 알 수 있고, 증명을 받아들일 수 있습니다.
단 가장 중요한 사실은 $x$가 신뢰 가능한 방법으로 정해져야 한다는 사실입니다. 만약 증명자가 $x$를 임의로 정할 수 있다면 그 말은 곧 $\beta_1, \dots , \beta_{r-1}$를 자신이 원하는 대로 정할 수 있다는 의미입니다.
5. Conclusion
이번 글을 통해 MPC를 이용해 Zero-Knowledge Proof을 수행하는 방법에 대해 알아보았습니다. 앞으로 누군가가 $\text{SHA256}(x) = 0^{256}$을 만족하는 $x$를 어떻게 영지식증명할 수 있는지 물어본다면 이 글에서 배운 내용을 토대로 자신 있게 대답할 수 있으면 좋겠습니다.
한편, 글 중간에도 언급했지만 NIZK는 Picnic이라는 Post-Qunatum Digital Signature에서도 활용됩니다. 비교적 최근에 제안된 구조이고 연구가 활발하게 이루어지고 있기 때문에 한번 살펴보시는 것도 재밌을 것으로 보입니다.