스킵 리스트

서론

다음 연산을 모두 $O(logn)$에 지원하는 자료구조가 필요합니다.

x를 추가한다.
x를 삭제한다.
x 이상의 원소 중 가장 작은 것을 출력한다.

C++에서는 std::set가 바로 이 역할을 하지만, Python에는 이런 내장 라이브러리가 없습니다. 그래서 외부 라이브러리를 쓰지 않는 한 레드-블랙 트리나 AVL 트리 등을 직접 구현해야 하는데, 트리 자료구조는 보통 rebalancing 과정이 복잡합니다.

한편, 트리의 틀을 벗어나면 스킵 리스트 (Skip List)라는 자료구조가 있습니다. “평균”이라는 말에서 추측할 수 있듯이, 랜덤을 사용한다는 특징이 있습니다. AVL 트리 등에 비해 구현이 매우 간단하기 때문에 Python으로 문제를 풀 때는 이 자료구조를 사용했는데, 사실 스킵 리스트에는 잘 알려지지 않은 다른 장점들이 있음을 알게되어 여기에 소개하기로 했습니다.

구조와 연산

스킵 리스트는 널리 알려져 있어 인터넷에 자료가 많으니, 구조는 간단하게만 정리하고 시간/공간 복잡도 증명은 생략합니다. (공간 복잡도는 $O(n)$입니다.)

구조

스킵 리스트는 여러 층의 링크드 리스트로 이루어져 있습니다. 스킵 리스트의 노드에는 각자 높이가 있고, $n$번째 층에는 높이가 $n$ 이상인 노드로 이루어진 링크드 리스트가 있습니다.

맨 처음에는 머리와 꼬리에 해당하는 dummy node 두 개만 주어져 있습니다.

head                                   tail
+-+                                     +-+
| |------------------------------------>| | 4층
|-|             +-+                     |-|
| |------------>|4|-------------------->| | 3층
|-|     +-+     |-|             +-+     |-|
| |---->|2|---->|4|------------>|8|---->| | 2층
|-|     |-|     |-|     +-+     |-|     |-|
| |---->|2|---->|4|---->|6|---->|8|---->| | 1층
+-+     +-+     +-+     +-+     +-+     +-+

탐색

$x$ 이상의 원소 중 가장 작은 것을 찾으려면, $x$에 대한 “이전 포인터 레이어”를 찾습니다.

(※주의: “이전 포인터 레이어”는 다른 자료에서도 쓰는 개념이 아니고 제가 만들어낸 용어입니다.)

이전 포인터 레이어는 다음과 같이 정의됩니다. 각 층마다 링크드 리스트의 노드 중 하나를 가리키는 포인터가 있는데, 그 노드는 “다음 노드가 꼬리이거나, 다음 노드의 값이 $x$ 이상인 마지막 노드”입니다. 예를 들어 $x = 7$이라면 이전 포인터 레이어는 아래 그림에서 #를 가리킵니다.

head                                   tail
+-+                                     +-+
|#|------------------------------------>| | 4층
|-|             +-+                     |-|
| |------------>|#|-------------------->| | 3층
|-|     +-+     |-|             +-+     |-|
| |---->|2|---->|#|------------>|8|---->| | 2층
|-|     |-|     |-|     +-+     |-|     |-|
| |---->|2|---->|4|---->|#|---->|8|---->| | 1층
+-+     +-+     +-+     +-+     +-+     +-+

층이 내려갈 수록 포인터는 오른쪽에 있기 때문에, 머리에서 시작해서 다음 노드로 가거나 아래 층으로 내려가는 것만으로 모든 포인터를 찾을 수 있습니다.

삽입

$x$를 스킵 리스트에 삽입해 봅시다.

$x$에 대한 이전 포인터 레이어를 찾습니다.
새로운 노드의 높이 $h$를 결정합니다. 어떻게 할까요? 먼저 $h = 1$로 둡니다. 그 후 루프를 돌리면서, 0.5의 확률로 앞/뒷면이 나오는 동전을 던집니다. 앞면이 나오면 $h$를 1 증가시키고, 뒷면이 나오면 루프를 끊습니다.
링크드 리스트에서 “다음 노드”를 삽입하는 것과 똑같은 방법으로 1층부터 $h$층까지 노드를 삽입합니다. $h$가 층의 개수보다 크다면, 링크드 리스트 한 층을 더 쌓아올립니다.

링크드 리스트만 알면 스킵 리스트도 구현할 수 있습니다!

head                                   tail
+-+                                     +-+
|#|------------------------------------>| | 4층
|-|             +-+                     |-|
| |------------>|#|-------------------->| | 3층
|-|     +-+     |-|         +-+ +-+     |-|
| |---->|2|---->|#|-------->|7|>|8|---->| | 2층
|-|     |-|     |-|     +-+ |-| |-|     |-|
| |---->|2|---->|4|---->|#|>|7|>|8|---->| | 1층
+-+     +-+     +-+     +-+ +-+ +-+     +-+

삭제

$x$를 삭제하는 것도 쉽습니다.

$x$에 대한 이전 포인터 레이어를 찾습니다.
$x$ 값을 가진 노드의 높이를 $h$라고 할 때, 링크드 리스트에서 “다음 노드”를 삭제하는 것과 똑같은 방법으로 1층부터 $h$층까지 노드를 삭제합니다.

head                                   tail
+-+                                     +-+
|#|------------------------------------>| | 4층
|-|             +-+                     |-|
| |------------>|#|-------------------->| | 3층
|-|     +-+     |-|             +-+     |-|
| |---->|2|---->|#|------------>|8|---->| | 2층
|-|     |-|     |-|     +-+     |-|     |-|
| |---->|2|---->|4|---->|#|---->|8|---->| | 1층
+-+     +-+     +-+     +-+     +-+     +-+

스킵 리스트 200% 활용하기

이제 스킵 리스트를 더 자유롭게 다루는 방법을 소개합니다.

더 자유로운 정렬 순서

std::set을 사용하려면 비교 연산자를 먼저 제시해 줘야 합니다. 비교 연산자를 중간에 갑자기 바꿀 수 없다는 것이죠. 하지만 이 글에서 구현한 스킵 리스트로는 가능한데, 그 이유는 애초에 비교 연산자 자체가 없기 때문입니다!

정렬된 데이터를 다루려고 만든 건데 비교 연산자가 없다니 무슨 소리일까요? 위의 ‘구조와 연산’ 섹션을 잘 보면, 노드 값의 비교는 탐색 과정에서만 사용됩니다. 탐색 과정에서 현재 보고 있는 노드의 값이 $x$ 이상이면 진행을 멈추고 아래 층으로 내려갑니다. 이 “노드의 값이 $x$ 이상”을 노드에 대한 boolean 함수로 바꿔도 똑같은 일을 할 수 있습니다.

물론 모든 함수가 다 되는 건 아니고, 각 노드에 대한 boolean 함수의 값이 첫 몇 개의 노드에 대해서는 거짓이고, 그 이후로는 모두 참이어야 합니다. 이분 탐색 또는 parametric search를 생각해 보면 이해하기 쉬울 것입니다.

예를 들어, 각 노드에 좌표평면 위의 선분이 하나씩 주어졌다고 합시다. 그리고 특정 $y$ 좌표에서 선분의 순서와 노드의 순서가 일치한다고 합시다. 이때 점 $(x, y)$는 어느 선분 사이에 위치할까요? 이를 찾으려면 boolean 함수를 “해당 노드의 선분을 $L$이라고 할 때, $(x, y)$, $L$의 아래쪽 정점, $L$의 위쪽 정점이 반시계방향으로 놓여 있으면 true, 아니면 false”로 잡으면 됩니다.

비교 연산자가 없다는 것도 이 의미입니다. 위의 예시에서 선분 사이의 비교 연산자는 존재하지 않습니다. 두 선분이 교차한다면, $y$ 좌표를 추가로 제공하지 않는 이상 한 선분이 다른 선분의 오른쪽에 있다고 말할 수 없기 때문입니다. 설령 $y$ 좌표를 제공하더라도, 두 선분을 비교할 필요가 없습니다. 선분이 “정렬”되어 있다는 사실은 알고리즘 자체의 논리, 불변량일 뿐, 코드에서 강제하는 성질이 아닙니다.

정렬 순서 깨뜨리기

정렬 순서가 그저 일종의 불변량이기 때문에, 이 불변량을 마음대로 깨뜨릴 수 있습니다. 탐색 연산을 하기 전까지만 정렬 순서를 복원하면 됩니다.

이러면 뭐가 좋을까요? 예를 들어, 위의 선분 예시를 다시 가져와 봅시다. $y$ 좌표가 더 낮아지면 선분의 정렬 순서가 바뀌므로 노드의 정렬 순서가 깨질 수 있습니다. 이를 해결하려면, 순서가 바뀌어야 하는 두 노드를 $y$ 좌표가 낮아지기 전에 미리 교환해 놓고, 그 다음에 $y$ 좌표를 낮추면 됩니다. 교환하면서 정렬 순서가 깨지지만, $y$ 좌표를 낮추면서 자동으로 정렬 순서가 복원되는 것이죠. 교환해야 하는 노드 쌍이 여러 개여도 각 쌍을 한 번씩 교환해 놓으면 아무 문제가 없습니다.

더 복잡한 정렬 순서

위 섹션에서 “노드 값에 대한 boolean 함수”가 아니라 “노드에 대한 boolean 함수”를 쓴 이유는, boolean 함수가 여러 노드를 참조할 수 있도록 하기 위함입니다.

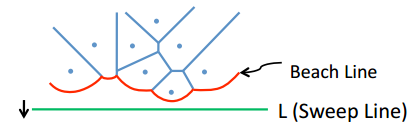
준선이 같고 초점만 다른 여러 개의 포물선이 있다고 합시다. 각 $x$ 좌표마다 포물선들의 최솟값을 찍으면 여러 개의 포물선으로 이루어진 곡선이 나올 것입니다. 이제 $x$ 좌표가 주어졌을 때, 그 곡선의 $x$ 좌표에 어떤 포물선이 있는지 $O(logn)$에 알아내야 합니다. 그리고 준선은 시간이 지날 수록 점점 내려가며, 포물선이 추가되거나 삭제될 수 있습니다. 이 작업은 보로노이 다이어그램을 구하는 알고리즘인 Fortune 알고리즘에서 사용됩니다.

준선이 계속 내려가면 포물선이 바뀌는 $x$ 좌표도 계속 변하기 때문에, 포물선이 바뀌는 $x$ 좌표가 아니라 포물선 자체를 스킵 리스트에 저장해 둡니다. 이제 노드 A가 어떤 $x$좌표에서 끝나는지 계산하려면, A 자신과 A의 다음 노드를 사용하면 됩니다. 이것으로 boolean 함수를 정의할 수 있습니다.

이터레이터

이전 포인터 레이어를 그대로 이터레이터로 가져다 쓸 수 있습니다. 특정 노드의 이전 포인터 레이어를 이터레이터라고 할 때, 이것을 다음 노드의 이터레이터로 “다음 노드의 높이”에 비례하는 시간에 바꿀 수 있습니다. 다음 노드의 높이를 $h$라고 할 때, 1층부터 $h$층까지의 포인터만 한 칸씩 오른쪽으로 밀어 주면 됩니다.

K번째 원소

스킵 리스트를 확장하면 “$k$번째로 작은 원소를 출력”도 평균 $O(logn)$에 구현할 수 있습니다. 각 링크드 리스트의 링크마다 “링크의 길이”를 저장해 놓으면 됩니다. 실제로 $k$번째 노드를 찾는 방법 및 노드를 추가하거나 삭제하는 방법은 독자에게 연습문제로 남겨 두겠습니다.

head                                   tail
+-+                                     +-+
| |5----------------------------------->| | 4층
|-|             +-+                     |-|
| |2----------->|4|3------------------->| | 3층
|-|     +-+     |-|             +-+     |-|
| |1--->|2|1--->|4|2----------->|8|1--->| | 2층
|-|     |-|     |-|     +-+     |-|     |-|
| |1--->|2|1--->|4|1--->|6|1--->|8|1--->| | 1층
+-+     +-+     +-+     +-+     +-+     +-+

단점

아쉽게도 저의 스킵 리스트 구현은 std::set보다 2배 가량 느립니다. 이 StackOverflow 질문에서 볼 수 있듯이, 캐시 히트를 잘 관리하면 좀 더 빠르게 할 수 있지만, vector로 구현하거나 Python 상에서 구현할 때에도 비슷한 효과를 기대할 수 있을지는 모르겠습니다. 단순한 단점이지만 때로는 치명적인 단점이 될 수도 있습니다.

결론

지금까지 스킵 리스트의 구조와 응용 방법을 다뤄 보았습니다.

속도와 응용 방법에 대해서는 아직 더 탐사할 영역이 남아 있습니다. 두 개의 open problem을 던지며 이 글을 마칩니다.

저의 스킵 리스트 구현을 더 빠르게 할 수 있을까요?
놀랍게도 스킵 리스트로 노드 추가 + 구간 합 쿼리를 구현할 수 있다고 합니다. 지원하는 쿼리의 범위, 속도, 난이도의 측면에서 스킵 리스트는 구간 쿼리에 얼마나 효과가 있을까요?