개요
프로그래밍 문제를 풀다 보면 종종 맞왜틀 (맞았는데 왜 틀려요)의 벽에 부딪히게 됩니다. 예제도 다 맞고, 열심히 생각해서 넣어본 여러 케이스들도 맞는데도 제출만 하면 틀렸다고 하고… 도무지 반례가 안 보일 때의 답답함은 말로 표현할 수가 없습니다.
연습용으로 문제를 풀 때에는 그나마 Polygon과 같은 전문 도구를 사용해서 스트레스를 돌리거나 견고하게 짜여진 테스트용 도구를 로컬에서 실행해보면서 반례를 찾을 수도 있습니다. Polygon의 사용법은 Acka1357 님의 글 문제 출제를 위한 플랫폼 - Polygon 사용하기에서 자세하게 확인할 수 있습니다. 하지만 항상 이런 도구를 사용할 수 있는 것은 아닙니다. 이를테면 각종 알고리즘 대회나 코딩 테스트 등이 그렇습니다.
이러한 대회 및 코딩 테스트에서는 외부 도구를 사용하는 것이 금지될 뿐 아니라 제대로 된 테스트 프로그램을 만들 시간 역시 촉박합니다. 기존에 작성해 둔 코드 역시 사용할 수가 없습니다. 그래서 이 글에서는 최대한 짧은 시간 내에 특정 코드에 대한 스트레스를 프로그램 자체적으로 돌려볼 수 있는 간이 테스터를 만드는 요령을 설명해보려 합니다.
요구 사항
우선 이 글은 C++을 기준으로 설명하고 있어, 다른 언어의 경우 일부 다른 방법을 사용해야 할 수 있습니다. 또한 표준 입력(stdin)으로 입력을 받아 표준 출력(stdout)에 출력하는 유형의 문제를 기준으로 설명합니다.
모든 종류의 테스터가 그렇지만 이러한 방법을 쓸 수 있는 문제는 효율성을 무시하고 쉽고 실수가 없을 법한 구현이 가능한 문제에 한정됩니다. 스트레스를 돌리는 것은 최소한 정답이 됨을 확신할 수 있는 코드가 있을 때에만 가능합니다. 많은 문제, 특히 대회 문제들에서는 효율성을 무시하고 완전 탐색을 수행하면 로직과 구현 난이도가 극도로 감소하는 경우가 많습니다. 이러한 비효율적인 코드에서도 충분히 빠른 시간 내에 답을 도출할 만한 작은 케이스들만을 테스트해보는 것이 스트레스 테스트의 주 원리입니다.1
또한 당연하지만 데이터의 형태는 간단할수록 좋으며 제약 조건이 적으면 랜덤 데이터를 생성하기에 훨씬 용이합니다. 답의 형태 역시 단답이면서 하나로 고정된 (스페셜 저지가 필요하지 않은) 문제이면 좋습니다.
예시 문제: 내 왼손에는 흑염룡이 잠들어 있다
우선 제 코드의 길이가 적당히 길고 아주 간단한 비효율적인 풀이가 존재하는 문제를 골라 보았습니다. 문제의 요구를 간단히 요약하면, $N \le 50000 $개의 정점으로 이루어진 간선에 가중치가 있는 트리가 하나 주어질 때, 각 정점에서 가장 먼 정점까지의 거리를 출력하는 문제입니다.
제한이 크기 때문에 $\mathcal{O}(N^2)$에는 풀리지 않을 것임을 예측할 수 있습니다. 따라서 풀이는 이보다 작은 시간 복잡도로 작성해야 하지만, 테스트를 위한 코드는 $\mathcal{O}(N^2)$의 시간 복잡도를 가져도 됩니다. 어차피 디버깅을 위한 반례를 찾는데 $N$이 20 이상인 큰 케이스는 시도할 가치가 없기 때문입니다.
다음은 저의 정답 코드에 일부 실수를 의도적으로 삽입한 틀린 $\mathcal{O}(N)$ 코드입니다. 문제 풀이가 목적이 아니기 때문에 설명은 따로 적지 않았습니다.
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
struct A {
int i, w;
};
const int N = 50005;
vector<A> adj[N];
pair<pii, pii> dp[N], dp2[N];
int par[N], pw[N];
bool v[N];
void upd(int i, pii x)
{
if (dp[i].first.first < x.first)
{
dp[i].second = dp[i].first;
dp[i].first = x;
}
else if (dp[i].second.first < x.second)
dp[i].second = x;
}
int f(int i, int p)
{
par[i] = p;
for (A x : adj[i])
{
if (x.i == p)
continue;
pw[x.i] = x.w;
int r = f(x.i, i);
r += x.w;
upd(i, { r, x.i });
}
return dp[i].first.first;
}
int g(int i, int c)
{
if (i == 0)
return 0;
if (!v[i])
{
v[i] = true;
int r = g(par[i], i);
r += pw[i];
upd(i, { r, par[i] });
}
return dp[i].first.second != c ? dp[i].first.first : dp[i].second.first;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n, i;
cin >> n;
for (i = 0; i < n - 1; i++)
{
int a, b, w;
cin >> a >> b >> w;
adj[a].push_back({ b, w });
adj[b].push_back({ a, w });
}
f(1, 0);
for (i = 1; i <= n; i++)
cout << g(i, 0) << '\n';
}
테스트를 위한 ‘진짜’ main 함수 작성하기
테스트를 할 때 중요한 것 중 하나는 기존 코드를 최대한 건드리지 않는 것입니다. 기존 코드에 수정을 가하면 가할수록 원래와 다른 의미의 코드가 될 가능성이 크기 때문입니다. 따라서 기존의 함수, 변수를 최대한 그대로 두기 위해 main 함수를 새로 작성할 것입니다.
스트레스를 돌릴 때에는 여러 케이스를 빠르게 실행해보는 것이 중요하기 때문에 프로그램 자체적으로 다중 테스트 케이스인 것처럼 실행하는 것이 편리합니다. 따라서, 새로운 main 함수는 다음과 같이 구성할 수 있습니다.
int main()
{
while (1)
{
// 데이터 생성
data = make_data;
// 틀린 코드, 맞는 코드 각각을 실행 후 답 회수
vector<int> wrong = main_wrong(data);
vector<int> correct = main_correct(data);
// 정답 확인
if (wrong != correct)
{
// 테스트 케이스 출력
cerr << data << endl;
cerr << "expected " << correct << ", found " << wrong << endl;
cin.get();
}
}
}
일반적인 문제를 만들 때 쓰이는 generator와 checker를 갖추고 이들의 실행까지 단 하나의 함수가 담당하고 있으며 validator는 생략한 형태입니다. 기존의 main 함수는 main_wrong과 같이 다른 이름으로 살짝 바꾸어주며, 입력을 표준 입력으로 주는 대신 인자로 넘겨주게끔 형태를 변환해 줍니다. 이는 정답 코드를 구현할 main_correct도 마찬가지입니다. 이제 이 의사 코드에 살을 붙여 이 문제에서 요구되는 형태로 완성해 보겠습니다.
int main()
{
while (1)
{
int n = rand() % 5 + 3;
vector<vector<int>> edges(n - 1);
for (int i = 2; i <= n; i++)
edges[i] = { i, rand() % (i - 1) + 1, rand() % 10 + 1 };
vector<int> wrong = main_wrong(edges);
vector<int> correct = main_correct(edges);
if (wrong != correct)
{
cerr << n << endl;
for (auto &x : edges)
cerr << x[0] << ' ' << x[1] << ' ' << x[2] << '\n';
cerr << "expected ";
for (int x : correct)
cerr << x << ' ';
cerr << ", found ";
for (int x : wrong)
cerr << x << ' ';
cerr << endl;
cin.get();
}
}
}
유효성 검사 없이 간단한 트리를 만드는 코드로, 균형이 잘 잡히지는 않지만 적당한 랜덤 트리를 만드는 데에는 이만큼 간편한 코드가 없습니다. 적당히 작은 n을 랜덤으로 설정하고, 각 정점이 자신보다 작은 번호의 정점과 연결되는 간선을 가지도록 하여 트리를 만들어줍니다. 출력 시에는 테스트 케이스 자체와 오답 코드, 정답 코드에서 나온 결과를 모두 출력해줍니다.
main_wrong 함수의 작성
데이터를 입력하는 형식을 바꾸었기 때문에 기존의 main 함수 (이제는 main_wrong 함수)도 바뀌어야 합니다. 따라서 입력을 받는 부분을 cin 대신 인자로 넘겨받은 변수의 값을 대입해주는 문장으로 바꾸고, cout에 출력하는 대신 함수가 반환할 벡터에 값을 추가하는 것으로 바꾸어 주어야 합니다.
또 한 가지 매우 중요한 것이 있는데, 바로 전역 변수의 초기화를 추가해줘야 한다는 점입니다. 전역 변수는 프로그램이 시작할 때 자동으로 초기화되기 때문에 크게 신경쓰지 않는 경우가 많지만, 여기서는 프로그램이 종료되지 않고 여러 번 반복해서 전체 작업을 수행하기 때문에 반드시 수동으로 초기화를 해야 합니다. 초기화가 필요한 변수의 종류나 엄밀한 범위를 고려하지 않고 전부 초기화 해주어도 됩니다. 어차피 효율성은 신경쓰지 않아도 되므로, 길게 생각하는 것이 손해입니다.
vector<int> main_wrong(vector<vector<int>> edges)
{
int n, i;
for (i = 0; i < N; i++)
{
adj[i].clear();
dp[i] = dp2[i] = { { 0, 0 }, { 0, 0 } };
par[i] = pw[i] = v[i] = 0;
}
n = edges.size() + 1;
for (i = 0; i < n - 1; i++)
{
vector<int> e = edges[i];
adj[e[0]].push_back({ e[1], e[2] });
adj[e[1]].push_back({ e[0], e[2] });
}
f(1, 0);
vector<int> ans;
for (i = 1; i <= n; i++)
ans.push_back(g(i, 0));
return ans;
}
맞는 코드의 작성
이제 맞는 코드를 작성해야 합니다. 맞는 코드는 말 그대로 ‘맞아야’ 합니다. 효율성은 뒤로 제치고, 어떻게 해서든 실수를 최대한 하지 않을 수 있는 방향으로 코딩을 해야 합니다. 예를 들어 선형 탐색 대신 이분 탐색을 하면 코드의 시간 복잡도가 좋아지더라도 실수 확률이 100% 증가한다면 이분 탐색을 하지 말아야 합니다. 이 과정에서 실수를 하게 될 경우 맞는 출력을 틀린다고 판단하여 크게 헤매게 될 수도 있습니다.
맞는 코드 작성 시에는 틀린 코드에서 사용한 전역 변수를 사용하지 않아야 합니다. 많은 경우 전역 변수는 틀린 코드에서 값을 변화시키기 때문에 항상 처음 케이스 생성 당시 상태로 그대로 남아있을 것이라고 기대해서는 안 됩니다. 그래서 가능하면 맞는 코드를 위한 별도의 전역 변수, 혹은 지역 변수를 만들어 사용하는 것이 바람직합니다.
입력 및 출력을 하는 부분은 main_wrong에서 복사를 해와도 좋으나, 반드시 빠뜨린 부분 없이 맞는 코드를 위한 변수들을 사용하도록 이름을 모두 교체해주어야 한다는 것에 주의해야 합니다. 또한 여기서도 역시 항상 처음에 전역 변수들에 대한 초기화를 수행해줘야 합니다.
vector<int> main_correct(vector<vector<int>> edges)
{
int n, i;
for (i = 0; i < N; i++)
c_adj[i].clear();
n = edges.size() + 1;
for (i = 0; i < n - 1; i++)
{
vector<int> e = edges[i];
c_adj[e[0]].push_back({ e[1], e[2] });
c_adj[e[1]].push_back({ e[0], e[2] });
}
vector<int> ans;
for (i = 1; i <= n; i++)
ans.push_back(sol(i, 0));
return ans;
}
마지막으로 이 문제의 ‘쉽고 비효율적인 풀이’인 sol 함수를 작성해 봅시다. 이 문제의 $\mathcal{O}(N^2)$ 풀이는 간단합니다. 트리를 완전탐색하면서, 각 노드에 연결된 자식 노드의 반환값에 가중치를 더한 것이 가장 큰 값을 부모로 반환해주면 됩니다.
int sol(int i, int p)
{
int ret = 0;
for (A x : c_adj[i])
{
if (x.i == p)
continue;
ret = max(ret, sol(x.i, i) + x.w);
}
return ret;
}
전체 코드는 다음과 같습니다.
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
struct A {
int i, w;
};
const int N = 50005;
vector<A> adj[N];
pair<pii, pii> dp[N], dp2[N];
int par[N], pw[N];
bool v[N];
void upd(int i, pii x)
{
if (dp[i].first.first < x.first)
{
dp[i].second = dp[i].first;
dp[i].first = x;
}
else if (dp[i].second.first < x.second)
dp[i].second = x;
}
int f(int i, int p)
{
par[i] = p;
for (A x : adj[i])
{
if (x.i == p)
continue;
pw[x.i] = x.w;
int r = f(x.i, i);
r += x.w;
upd(i, { r, x.i });
}
return dp[i].first.first;
}
int g(int i, int c)
{
if (i == 0)
return 0;
if (!v[i])
{
v[i] = true;
int r = g(par[i], i);
r += pw[i];
upd(i, { r, par[i] });
}
return dp[i].first.second != c ? dp[i].first.first : dp[i].second.first;
}
vector<int> main_wrong(vector<vector<int>> edges)
{
int n, i;
for (i = 0; i < N; i++)
{
adj[i].clear();
dp[i] = dp2[i] = { { 0, 0 }, { 0, 0 } };
par[i] = pw[i] = v[i] = 0;
}
n = edges.size() + 1;
for (i = 0; i < n - 1; i++)
{
vector<int> e = edges[i];
adj[e[0]].push_back({ e[1], e[2] });
adj[e[1]].push_back({ e[0], e[2] });
}
f(1, 0);
vector<int> ans;
for (i = 1; i <= n; i++)
ans.push_back(g(i, 0));
return ans;
}
vector<A> c_adj[N];
int sol(int i, int p)
{
int ret = 0;
for (A x : c_adj[i])
{
if (x.i == p)
continue;
ret = max(ret, sol(x.i, i) + x.w);
}
return ret;
}
vector<int> main_correct(vector<vector<int>> edges)
{
int n, i;
for (i = 0; i < N; i++)
c_adj[i].clear();
n = edges.size() + 1;
for (i = 0; i < n - 1; i++)
{
vector<int> e = edges[i];
c_adj[e[0]].push_back({ e[1], e[2] });
c_adj[e[1]].push_back({ e[0], e[2] });
}
vector<int> ans;
for (i = 1; i <= n; i++)
ans.push_back(sol(i, 0));
return ans;
}
int main()
{
while (1)
{
int n = rand() % 5 + 3;
vector<vector<int>> edges(n - 1);
for (int i = 0; i < n - 1; i++)
edges[i] = { i + 2, rand() % (i + 1) + 1, rand() % 10 + 1 };
vector<int> wrong = main_wrong(edges);
vector<int> correct = main_correct(edges);
if (wrong != correct)
{
cerr << n << endl;
for (auto &x : edges)
cerr << x[0] << ' ' << x[1] << ' ' << x[2] << '\n';
cerr << "expected ";
for (int x : correct)
cerr << x << ' ';
cerr << ", found ";
for (int x : wrong)
cerr << x << ' ';
cerr << endl;
cin.get();
}
}
}
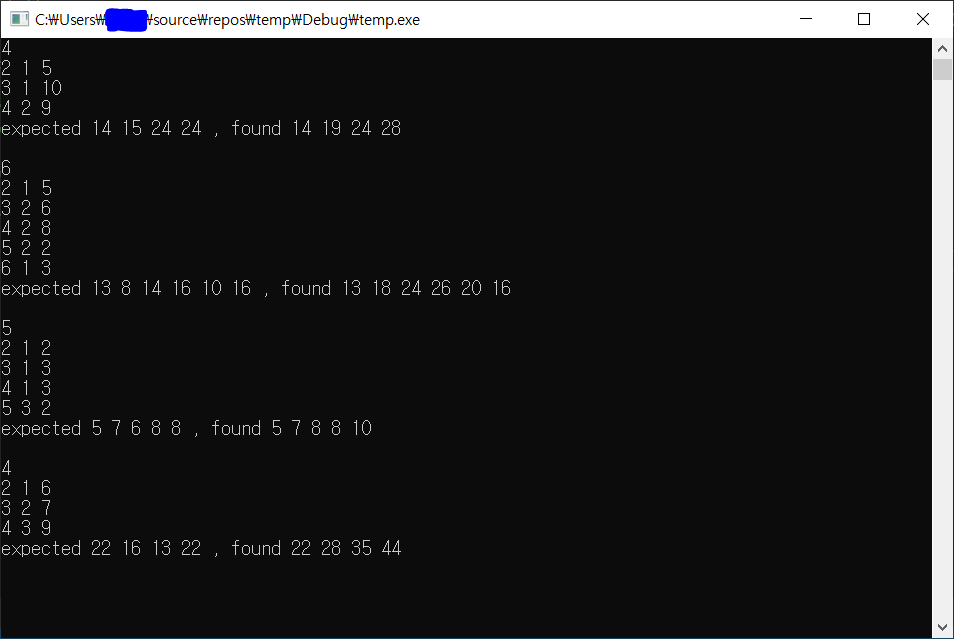
실행 결과
이제 이 코드가 반례를 잘 찾아줄 수 있는지 한 번 실행해 보겠습니다.
개선 사항
루프를 돌릴 때마다 케이스를 항상 출력해보는 것도 좋은 방법입니다. 때로는 다중 테스트 케이스 형태로 변환시키는 과정에서 이런 저런 실수가 발생하기도 하고, 특히 데이터 생성 과정에서 문제가 발생하는 경우가 많습니다. 이러한 부분들에서 실수가 있지 않은지를 항상 확인할 수 있도록 하면 더 빠르게 테스터를 디버깅할 수 있습니다.
또한 콘솔에 출력을 할 경우 데이터를 모아두기가 번거로워지는 문제도 있습니다. 이를 위해 반례를 하나 찾을 때마다 멈추는 대신 특정 개수의 반레를 찾을 때까지 지속적으로 화면에 출력하게 한 뒤, 프로그램을 실행할 때 리다이렉트를 통해 화면 대신 파일에 그 내용을 쓰게 하면 손쉽게 반례 데이터들을 모아둘 수 있습니다.
마치며
코드포스와 같이 기존의 도구를 사용해도 되는 대회에서는 매번 이런 수고를 할 필요는 없습니다. 그러나 프로그래밍 대회나 코딩 테스트에서는 이것이 불가능하고, 시간이 곧 성적이며 오답 페널티 역시 무시할 수 없습니다. 최대한 신속하게 프로그램을 검증할 수 있는 방법을 알아두는 것은 분명히 유용합니다. 실제로 이와 같은 방법을 ICPC에서도 사용하여 재미를 본 경험도 있습니다. 이 글과 같은 방법, 또는 더 좋은 자신만의 방법이 있다면 평소에 연습해두는 것을 추천합니다.
-
안타깝게도, 코딩 테스트의 경우 대다수의 문제가 논리적인 해결 능력보다는 정교한 구현에 초점을 두고 있어 이 방법을 쓰기가 쉽지 않은 경우가 많습니다. ↩