Differential Cryptanalysis on 4-round DES
서론
이번 글에서는 차분 분석 (Differential cryptanalysis)가 무엇인지 간략하게 살펴보고, 4-round DES에 대한 차분 공격을 예시로 알아보고자 합니다.
본론
차분 분석
차분 분석을 간단하게 말하자면, 어떤 함수 $f$가 주어져있을 때 $x, y$ 에 대해서 $(y - x, f(y) - f(x))$ 가 일정 확률로 특정 관계성을 만족하는 것을 이용하는 분석 방법 중 하나입니다. 이렇게만 이야기하면 쉽게 와닿지 않을 것 같아서 예시를 준비해봤습니다.
S-box
DES, AES와 같은 암호들을 살펴보면, 대부분의 연산이 선형 계산으로 이루어져 있습니다. 즉, 어떤 입력 $x$에 대해서 $ax + b$ 꼴을 계산하는 것과 같아서 쉽게 역연산이 가능합니다. 하지만 도중에 substitution 연산을 하나 넣어서 선형성을 깨는데, 이 때 이용되는 것이 S-box입니다. S-box는 무작위로 shuffle된 permutation으로 이해할 수 있습니다. 예를 들어 0부터 255까지의 input을 받고 0부터 255까지의 output을 내놓는 S-box를 다음과 같이 쉽게 만들어볼 수 있습니다.
import random
S = list(range(256))
random.shuffle(S)
이 때 우리가 S 에 어떤 값 x를 주면, 이는 S[x]라는 무작위로 섞인 값으로 바뀌게 될 것입니다. 이 때 이 S 에는 선형 관계성이 없기 때문에, 암호를 분석하는데 어려움을 줍니다.
DES S-BOX에 차분 분석을 해보자!
DES는 16개의 라운드로 구성되어 있습니다.
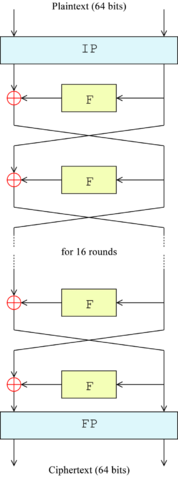
한 라운드는 다음과 같은 과정을 거칩니다.
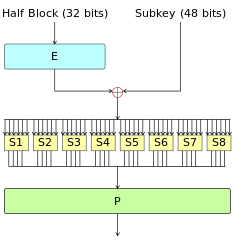
살펴보면 32-bit input이 expand(E) 과정을 거친 뒤 subkey와 XOR 되고, 각 비트가 여덟 갈래로 나뉘어 8개의 S-box를 거친 뒤 permutate(P) 과정을 거치는 것을 볼 수 있습니다. 이 때 사용되는 S-box는 각각 6비트 input을 받고 4비트 output을 내놓는 S-box임을 알 수 있습니다.
이제 이 중 첫 번째 S-box인 S1에 대해서 한 번 차분 분석을 해봅시다. DES implementation은 [2]의 pydes를 참고하여 사용했습니다.
앞서 얘기한 것처럼 input $x, y$에 대해서 $(y - x, f(y) - f(x))$ 의 분포를 살펴볼 것입니다. 이는 다음과 같이 코드를 작성할 수 있겠습니다. 이 때 XOR을 사용하는 이유는, DES나 AES와 같은 암호에서는 덧셈과 뺄셈이 모두 XOR과 동일하기 때문이라고 이해하시면 되겠습니다.
S1 = [
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
[0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
[4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],
]
def substitute(v):
v = format(v, '06b')
row = int(v[0] + v[5], 2)
column = int(v[1:5], 2)
res = S1[row][column]
return res
popu = [[ 0 for j in range(0x10) ] for i in range(0x40)]
for x in range(0x40):
for y in range(0x40):
popu[x ^ y][substitute(y) ^ substitute(x)] += 1
for i in range(0x40):
print(i, popu[i])
결과는 다음과 같습니다.
0 [64, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
1 [0, 0, 0, 6, 0, 2, 4, 4, 0, 10, 12, 4, 10, 6, 2, 4]
2 [0, 0, 0, 8, 0, 4, 4, 4, 0, 6, 8, 6, 12, 6, 4, 2]
3 [14, 4, 2, 2, 10, 6, 4, 2, 6, 4, 4, 0, 2, 2, 2, 0]
4 [0, 0, 0, 6, 0, 10, 10, 6, 0, 4, 6, 4, 2, 8, 6, 2]
5 [4, 8, 6, 2, 2, 4, 4, 2, 0, 4, 4, 0, 12, 2, 4, 6]
...
58 [6, 4, 6, 4, 6, 8, 0, 6, 2, 2, 6, 2, 2, 6, 4, 0]
59 [2, 6, 4, 0, 0, 2, 4, 6, 4, 6, 8, 6, 4, 4, 6, 2]
60 [0, 10, 4, 0, 12, 0, 4, 2, 6, 0, 4, 12, 4, 4, 2, 0]
61 [0, 8, 6, 2, 2, 6, 0, 8, 4, 4, 0, 4, 0, 12, 4, 4]
62 [4, 8, 2, 2, 2, 4, 4, 14, 4, 2, 0, 2, 0, 8, 4, 4]
63 [4, 8, 4, 2, 4, 0, 2, 4, 4, 2, 4, 8, 8, 6, 2, 2]
살펴보면, 0이 생각보다 많습니다. 고르게 분포해있다면 x ^ y에 따라서 S[x] ^ S[y] 값이 고르게 4개씩 나와야 했을 것입니다. 하지만 x ^ y = 1일 때를 보면, S[x] ^ S[y] = 10 일 가능성이 무려 12/64인 것을 볼 수 있습니다.
그렇다면 이것을 어떻게 쓸 수 있을까요?
앞서 말했듯이 S-box를 제외하면 나머지 연산들은 모두 선형성을 지닙니다. 그러므로 $x$가 주어져도 실제 값은 S-box를 거치기 전까지는 $ax + b$꼴임을 알 수 있습니다. 이러한 선형성은 $y - x$ 에 대해서도 유지가 됩니다. $(ay + b) - (ax + b) = a(y - x)$ 이므로, $y - x$를 고정시켜 놓는다면 S-box를 거치기 직전의 값 $a(y - x)$를 알 수 있고, 또한 위에서 구한 관계성을 이용한다면 적절한 확률로 S-box를 거친 뒤의 차이 또한 알 수 있을 것입니다.
4-round DES를 공격해보자!
이제 4-round DES를 공격하는 방법에 대해 알아봅시다.
특성 (Characteristic)
[3] 의 논문에서는 $i$-round DES에 대해 input을 넣었을 때 특정 확률로 나오는 output들을 $i$-round DES의 characteristic(특성)으로 정의하고 이에 대해서 정리해놨습니다.
1-round DES에 대해서 가장 간편하게 살펴볼 수 있는 특성은 다음일 것입니다. 이 때 input을 pair로 기술했는데, 왼쪽이 64-bit input의 왼쪽 32-bit, 오른쪽이 오른쪽 32-bit라고 이해하시면 되겠습니다.
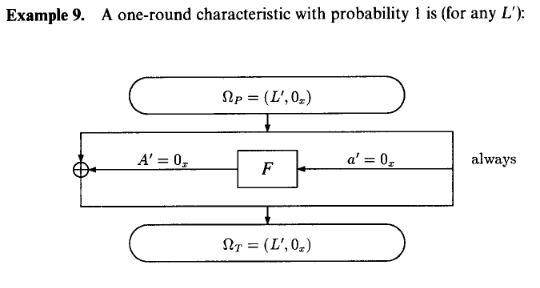
살펴보시면 $a’$가 0, 즉 같은 값 $x, y$가 들어가면 당연히 그 차이 또한 $F(x) - F(y) = 0$이므로 $A’$가 0이라고 할 수 있을 것입니다. 그러므로 다음과 같은 성질이 임의의 $L’$에 대해서 성립합니다.
또한 여기서 더 나아가서 2-round의 경우 더 재밌는 특성을 볼 수 있습니다.
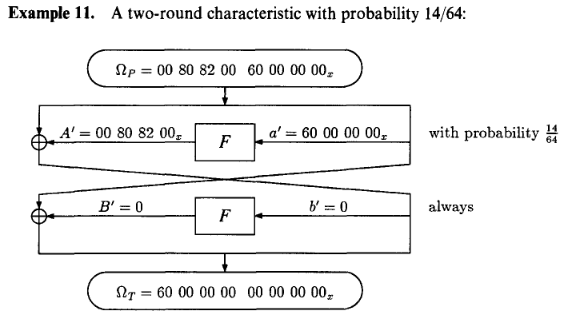
$a’$가 60 00 00 00일 경우 14/64 확률로 00 80 82 00이 된다는 특성을 가지고 있습니다. (이는 첫 번째 S-box의 특성에서 기인합니다) 그리고 이렇게 나온 $A’$는 앞 32-bit의 00 80 82 00과 상쇄되어 $0$이 되고, 곧 60 00 00 00 00 00 00 00이라는 output 차이를 낳게 됩니다.
Attacking 4-round DES
4-round DES를 공격하기 위해서는 어떤 특성을 사용해야 할까요? 논문에서는 다음과 같은 특성을 사용했습니다.
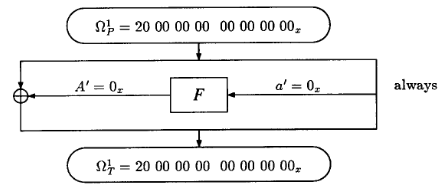
이 때 각 round의 값들에 대한 명칭은 다음 그림을 참조해주세요.
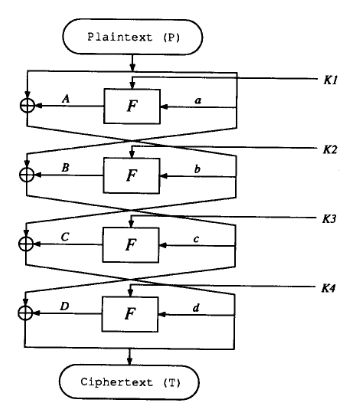
위 특성을 사용하게 되면 $a’ = A’ = 0$이고, $b’ = 20\ 00\ 00\ 00$이 되는 것을 알 수 있습니다. 그리고 이 때 $b’$가 $F$를 거치게 되면, S2부터 S8까지의 input의 경우 difference가 0이여서 S1의 output에 대해서만 difference가 발생하고 곧 28비트의 output의 difference가 항상 0이 되게 됩니다.
이 때, $a’ \oplus B’ = c’ = D’ \oplus l’$ ($l’$은 output의 왼쪽 32-bit의 difference) 이므로 $D’ = a’ \oplus l’ \oplus B’$를 얻을 수 있고, 우리는 $a’, l’$과 $B’$의 28비트를 알고 있으므로 $D’$의 28비트를 알 수 있고, 이는 S2~S8의 output과 관련된 값들입니다. 그리고 또한 우리는 $d$ 값들을 ciphertext $T$로부터 알고 있으므로 (오른쪽 32-bit), $K4$를 6비트씩 brute-force하는 것이 가능합니다.
이를 코드로 하나씩 작성해봅시다.
Getting subkey K4
우선 pydes의 round 관련 코드를 16에서 4로 바꿉니다.
def run(self, key, text, action=ENCRYPT, padding=False):
if len(key) < 8:
raise "Key Should be 8 bytes long"
elif len(key) > 8:
key = key[:8] #If key size is above 8bytes, cut to be 8bytes long
self.password = key
self.text = text
if padding and action==ENCRYPT:
self.addPadding()
elif len(self.text) % 8 != 0:#If not padding specified data size must be multiple of 8 bytes
raise "Data size should be multiple of 8"
self.generatekeys() #Generate all the keys
text_blocks = nsplit(self.text, 8) #Split the text in blocks of 8 bytes so 64 bits
result = list()
for block in text_blocks:#Loop over all the blocks of data
block = string_to_bit_array(block)#Convert the block in bit array
block = self.permut(block,PI)#Apply the initial permutation
print(block)
g, d = nsplit(block, 32) #g(LEFT), d(RIGHT)
tmp = None
# for i in range(16): #Do the 16 rounds
for i in range(4): # 4-round DES
d_e = self.expand(d, E) #Expand d to match Ki size (48bits)
if action == ENCRYPT:
tmp = self.xor(self.keys[i], d_e)#If encrypt use Ki
else:
tmp = self.xor(self.keys[15-i], d_e)#If decrypt start by the last key
tmp = self.substitute(tmp) #Method that will apply the SBOXes
tmp = self.permut(tmp, P)
tmp = self.xor(g, tmp)
g = d
d = tmp
result += self.permut(d+g, PI_1) #Do the last permut and append the result to result
final_res = bit_array_to_string(result)
if padding and action==DECRYPT:
return self.removePadding(final_res) #Remove the padding if decrypt and padding is true
else:
return final_res #Return the final string of data ciphered/deciphered
특히 코드를 작성하면서 주의할 점이 block = self.permut(block,PI)와 result += self.permut(d+g, PI_1) 입니다. DES는 맨 처음에 permutation을 한 번 하고 마지막에 permutation을 또 한 번 하는데, 해당 논문에서는 해당 permutation은 쉽게 역연산이 가능하기 때문에 고려하지 않는다고 서술해두었습니다. 그러므로 논문대로 20 00 00 00 00 00 00 00의 difference를 가지는 input을 생성하려면 6번째 바이트의 2번째 비트(0x40) 을 flip 해줘야 합니다. 이를 바탕으로 한 pair에 대해서 다음과 같이 작성이 가능합니다.
import itertools
import os
from pydes import *
def permutate_rev(b, table):
res = [None for _ in range(len(b))]
for i in range(len(b)):
res[table[i] - 1] = b[i]
return res
key = os.urandom(8)
t1 = os.urandom(8)
t2 = bytes([v ^ 0x40 if i == 5 else v for i, v in enumerate(t1)])
cipher = des()
e1 = string_to_bit_array([ord(v) for v in cipher.encrypt(key, t1)])
e2 = string_to_bit_array([ord(v) for v in cipher.encrypt(key, t2)])
e1 = permutate_rev(e1, PI_1)
e2 = permutate_rev(e2, PI_1)
lp = [x ^ y for x, y in zip(e1[:32], e2[:32])]
lpt = permutate_rev(lp, P)
# Go through F
d1 = cipher.expand(e1[32:], E)
d2 = cipher.expand(e2[32:], E)
def substitute_partial(block, S_BOX):
row = int(str(block[0])+str(block[5]),2)
column = int(''.join([str(x) for x in block[1:][:-1]]),2)
val = S_BOX[row][column]
bin = binvalue(val, 4)
return [int(x) for x in bin]
for i in range(1, 8):
for ki in itertools.product(range(2), repeat=6):
b1 = [x ^ y for x, y in zip(ki, d1[6 * i:6 * i + 6])]
b2 = [x ^ y for x, y in zip(ki, d2[6 * i:6 * i + 6])]
b1 = substitute_partial(b1, S_BOX[i])
b2 = substitute_partial(b2, S_BOX[i])
Dpi = [x ^ y for x, y in zip(b1, b2)]
if Dpi == lpt[4 * i:4 * i + 4]:
print(i, ki)
e1, e2는 암호화된 값이고, PI_1을 역연산해 값을 얻어줍니다. lp는 $l’$에 해당하고, 이를 P로 뒤집어주면 S2 ~ S8의 output들에 해당하는 위치의 값들을 알 수 있습니다.
그 뒤 $d_1, d_2$를 구해주고, S2 ~ S8 위치에 해당하는 subkey K4의 partial 6-bit ki의 후보들을 얻을 수 있습니다.
이제 이를 여러 개의 pair에 대해서 확장합시다. 논문에서는 8개의 pair면 충분하다고 언급하고 있습니다.
import itertools
import os
from pydes import *
def permutate_rev(b, table):
res = [None for _ in range(len(b))]
for i in range(len(b)):
res[table[i] - 1] = b[i]
return res
key = os.urandom(8)
K4_cand = [None] * 8
for _ in range(8):
t1 = os.urandom(8)
t2 = bytes([v ^ 0x40 if i == 5 else v for i, v in enumerate(t1)])
cipher = des()
e1 = string_to_bit_array([ord(v) for v in cipher.encrypt(key, t1)])
e2 = string_to_bit_array([ord(v) for v in cipher.encrypt(key, t2)])
e1 = permutate_rev(e1, PI_1)
e2 = permutate_rev(e2, PI_1)
lp = [x ^ y for x, y in zip(e1[:32], e2[:32])]
lpt = permutate_rev(lp, P)
# Go through F
d1 = cipher.expand(e1[32:], E)
d2 = cipher.expand(e2[32:], E)
def substitute_partial(block, S_BOX):
row = int(str(block[0])+str(block[5]),2)
column = int(''.join([str(x) for x in block[1:][:-1]]),2)
val = S_BOX[row][column]
bin = binvalue(val, 4)
return [int(x) for x in bin]
for i in range(1, 8):
st = set()
for ki in itertools.product(range(2), repeat=6):
b1 = [x ^ y for x, y in zip(ki, d1[6 * i:6 * i + 6])]
b2 = [x ^ y for x, y in zip(ki, d2[6 * i:6 * i + 6])]
b1 = substitute_partial(b1, S_BOX[i])
b2 = substitute_partial(b2, S_BOX[i])
Dpi = [x ^ y for x, y in zip(b1, b2)]
if Dpi == lpt[4 * i:4 * i + 4]:
st.add(ki)
if K4_cand[i] is None:
K4_cand[i] = st
else:
K4_cand[i] &= st
print(K4_cand)
실행해보면 다음과 같은 결과를 얻을 수 있습니다. K4의 첫 6비트를 제외한 나머지를 확정적으로 구하는 것을 구할 수 있습니다.
[None, {(1, 0, 1, 1, 0, 0)}, {(1, 0, 1, 1, 1, 0)}, {(1, 0, 0, 0, 0, 1)}, {(0, 0, 1, 1, 1, 0)}, {(1, 1, 1, 0, 1, 1)}, {(1, 0, 0, 0, 1, 0)}, {(1, 0, 0, 1, 1, 0)}]
Recovering the key
이제 brute-force를 통해서 key를 복구해봅시다. 이를 위해서는 Key를 만드는 과정을 이해할 필요가 있습니다.
def generatekeys(self):#Algorithm that generates all the keys
self.keys = []
key = string_to_bit_array(self.password)
key = self.permut(key, CP_1) #Apply the initial permut on the key
g, d = nsplit(key, 28) #Split it in to (g->LEFT),(d->RIGHT)
for i in range(16):#Apply the 16 rounds
g, d = self.shift(g, d, SHIFT[i]) #Apply the shift associated with the round (not always 1)
tmp = g + d #Merge them
self.keys.append(self.permut(tmp, CP_2)) #Apply the permut to get the Ki
우선 key는 8 바이트이지만 key = self.permut(key, CP_1)를 거치면서 7 바이트가 됩니다. 버려진 1바이트의 정보는 암호화의 어디에도 사용되지 않는데, parity 등에 사용하기 위함이라는 이야기가 있습니다.
그리고 7바이트를 g, d = self.shift(g, d, SHIFT[i])를 통해서 계속 변환하면서, self.permut(tmp, CP_2)를 통해서 7바이트 중 6바이트만을 subkey로 내보내게 됩니다.
이를 바탕으로 다음과 같이 코드를 작성해봅시다.
K4_2 = []
for i in range(1, 8):
assert len(K4_cand[i]) == 1
K4_2 += list(K4_cand[i].pop())
CP_2_ = CP_2 + [9, 18, 22, 25, 35, 38, 43, 54]
CP_1_ = CP_1 + [8, 16, 24, 32, 40, 48, 56, 64]
for K4_1 in itertools.product(range(2), repeat=6):
for K_remain in itertools.product(range(2), repeat=8):
K4 = list(K4_1) + K4_2 + list(K_remain)
g, d = nsplit(permutate_rev(K4, CP_2_), 28)
for i in range(3, -1, -1):
g, d = cipher.shift(g, d, 28 - SHIFT[i])
key_ = g + d + [0] * 8
key_ = bit_array_to_string(permutate_rev(key_, CP_1_))
for i in range(100):
pt = os.urandom(8)
ct1 = cipher.encrypt(key, pt)
ct2 = cipher.encrypt(key_, pt)
if ct1 != ct2:
break
else:
print("FOUND")
print(string_to_bit_array(key))
print(string_to_bit_array(key_))
테스트해보면 다음과 같이 잘 구하는 것을 볼 수 있습니다. 매 8번째 비트가 사용되지 않으므로 그 부분을 감안하고 보시면 되겠습니다.
FOUND
[1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1]
[1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0]
Full code
import itertools
import os
from pydes import *
def permutate_rev(b, table):
res = [None for _ in range(len(b))]
for i in range(len(b)):
res[table[i] - 1] = b[i]
return res
key = os.urandom(8)
K4_cand = [None] * 8
for _ in range(8):
t1 = os.urandom(8)
t2 = bytes([v ^ 0x40 if i == 5 else v for i, v in enumerate(t1)])
cipher = des()
e1 = string_to_bit_array([ord(v) for v in cipher.encrypt(key, t1)])
e2 = string_to_bit_array([ord(v) for v in cipher.encrypt(key, t2)])
e1 = permutate_rev(e1, PI_1)
e2 = permutate_rev(e2, PI_1)
lp = [x ^ y for x, y in zip(e1[:32], e2[:32])]
lpt = permutate_rev(lp, P)
# Go through F
d1 = cipher.expand(e1[32:], E)
d2 = cipher.expand(e2[32:], E)
def substitute_partial(block, S_BOX):
row = int(str(block[0])+str(block[5]),2)
column = int(''.join([str(x) for x in block[1:][:-1]]),2)
val = S_BOX[row][column]
bin = binvalue(val, 4)
return [int(x) for x in bin]
for i in range(1, 8):
st = set()
for ki in itertools.product(range(2), repeat=6):
b1 = [x ^ y for x, y in zip(ki, d1[6 * i:6 * i + 6])]
b2 = [x ^ y for x, y in zip(ki, d2[6 * i:6 * i + 6])]
b1 = substitute_partial(b1, S_BOX[i])
b2 = substitute_partial(b2, S_BOX[i])
Dpi = [x ^ y for x, y in zip(b1, b2)]
if Dpi == lpt[4 * i:4 * i + 4]:
st.add(ki)
if K4_cand[i] is None:
K4_cand[i] = st
else:
K4_cand[i] &= st
K4_2 = []
for i in range(1, 8):
assert len(K4_cand[i]) == 1
K4_2 += list(K4_cand[i].pop())
CP_2_ = CP_2 + [9, 18, 22, 25, 35, 38, 43, 54]
CP_1_ = CP_1 + [8, 16, 24, 32, 40, 48, 56, 64]
for K4_1 in itertools.product(range(2), repeat=6):
for K_remain in itertools.product(range(2), repeat=8):
K4 = list(K4_1) + K4_2 + list(K_remain)
g, d = nsplit(permutate_rev(K4, CP_2_), 28)
for i in range(3, -1, -1):
g, d = cipher.shift(g, d, 28 - SHIFT[i])
key_ = g + d + [0] * 8
key_ = bit_array_to_string(permutate_rev(key_, CP_1_))
for i in range(100):
pt = os.urandom(8)
ct1 = cipher.encrypt(key, pt)
ct2 = cipher.encrypt(key_, pt)
if ct1 != ct2:
break
else:
print("FOUND")
print(string_to_bit_array(key))
print(string_to_bit_array(key_))
결론
본래 다른 주제에 대해서 개인 연구를 진행하고 있었는데, 저번 달에도 결과가 잘 나오지 않았고 이번 달에도 결과가 나오지 않아 해당 연구의 바탕이 되는 differential cryptanalysis에 대해서 간단한 글을 작성하게 되었습니다.
국내에 관련 주제의 글을 많이 찾아볼 수 없기 때문에, 이를 통해서 차분 분석에 대해 간단하게 입문하실 수 있으면 좋겠습니다.
참고 문헌
- https://en.wikipedia.org/wiki/Differential_cryptanalysis
- pydes https://github.com/RobinDavid/pydes
- Differential cryptanalysis of DES-like cryptosystems https://link.springer.com/content/pdf/10.1007/BF00630563.pdf