blisstoner's profile image

blisstoner

July 18, 2021 11:00

1. Introduction

이전에 썼던 글들을 통해

• MPC를 이용해 Zero-Knowledge Proof를 만들 수 있다
• Fiat-Shamir Transform을 이용해 Zero-Knowledge Proof을 Non-Interactive로 변경할 수 있다
• NIZK를 통해 전자 서명을 만들 수 있다

는 것을 알게 되었습니다. 이미 RSA 혹은 ECC 등을 이용한 전자서명이 존재하지만 RSA 혹은 ECC 등은 아직 증명되지 않은 정수론/대수학적 안전성을 가정해야 하는 반면, MPC를 이용한 전자서명은 오로지 해시 함수의 안전성에만 의존한다는 장점이 있습니다. 더 나아가 양자컴퓨터가 개발된 이후에도 안전한 양자 내성 성질을 가지고 있습니다.

전자서명을 평가하는 기준으로는 서명의 크기와 서명의 생성/검증 속도가 있을 수 있고, MPC를 이용한 전자서명이 효율적이려면 크기를 줄이거나 생성/검증 속도를 높여야 합니다.

MPC에서 XOR 혹은 덧셈과 같은 선형 연산은 별도의 커뮤니케이션을 필요로 하지 않고 각 사용자가 독립적으로 수행할 수 있습니다. 반면 AND 혹은 곱셈과 같은 비선형 연산은 그렇지가 않아서 선형 연산에 비해 비싼 연산입니다.

AES는 구조적으로 AND 연산이 아주 많이 들어가기 때문에 LowMC라는, AND 연산을 많이 줄인 암호를 만들고 이 암호를 MPC에서 이용하고 있습니다.

그러나 LowMC는 비교적 최근에 제안된 구조인 만큼 아직 안전성이 완벽하게 증명되었다고 볼 수 없고, 실제로 굉장히 다양한 공격이 제안되어 파라미터를 고치는 일이 여러 번에 걸쳐 발생했습니다.

그렇기 때문에 다시 LowMC 대신 긴 시간에 걸쳐 검증된 AES를 이용해 MPC를 만들려는 시도가 있어왔습니다. 기존에는 수많은 AND 연산으로 인해 성능 저하를 필연적으로 가져올 수 밖에 없었던 AES인데 이 상황을 어떤 식으로 개선했는지 같이 알아보겠습니다.

2. AES

AES는 2001년 NIST의 공모를 통해 선정된 암호화 방식입니다. AES는 한 칸이 1바이트인 4 by 4 매트릭스를 하나의 블록으로 두고 Substitution과 Permutation을 반복하는 구조입니다. 다양한 공격들이 제시되었으나 Full round 기준 전수조사보다 겨우 4배 정도 빠른 방법만이 찾아졌을 정도로 견고합니다.

AES에 있는 유일한 비선형 연산은 바이트 단위로 수행되는 S-box 연산입니다. S-box연산은 $GF(2^8)$에서의 inverse 연산입니다. S-box 연산을 제외한 나머지 연산들은 모두 선형으로 표현 가능합니다.

이 S-box 연산을 비트 단위로 나타낼 때에는 254차식이 나옵니다. 이렇게 차수가 크기 때문에 AES는 대략 6400개의 AND 게이트를 필요로 합니다. LowMC가 대략 600개의 AND 게이트를 필요로 하는 것과 비교할 때 큰 차이가 있습니다.

3. BBQ

BBQ는 AES를 이용한 MPC-based 전자서명의 이름입니다.(논문 제목 : BBQ: Using AES in Picnic Signatures)

BBQ에서의 핵심은 AES를 Boolean circuit으로 생각하는 대신 Arithmetic circuit으로 생각하자는 아이디어였습니다.

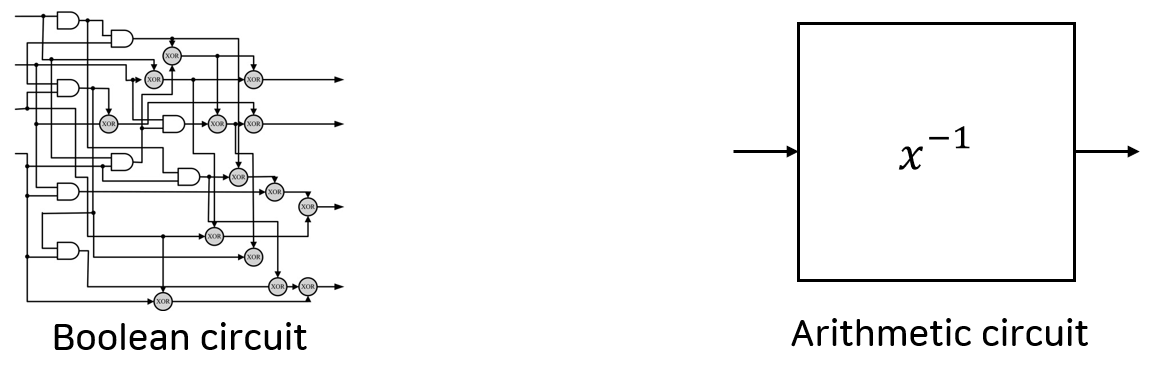
AES를 Boolean circuit으로 생각할 경우 위에서 언급한 것과 같이 AND 게이트가 많이 필요한 점으로 인해 많이 비효율적입니다. 그런데 Arithmetic circuit으로 생각을 한다면 inverse 연산을 254차식으로 생각할 필요 없이 그저 하나의 연산으로 둘 수 있습니다.

그러면 결국 Arithmetic circuit에서 inverse 연산을 어떻게 할 수 있는지를 고민해볼 필요가 있게 됩니다.

Arithmetic circuit에서 inverse 연산을 수행하는 방법을 다루기 전, MPC에 대한 기억을 상기시킬겸 MPC에서의 여러 연산들을 수행하는 방법을 익혀봅시다. 그냥 바로 연산을 수행하는 대신 앞으로 소개할 번거로운 절차를 거쳐서 수행하는 이유는 Zero-Knowledge 성질을 달성하기 위해서입니다.

먼저 원래 circuit에서의 변수 $x$를 나누어 가지는 과정에서 각 사용자는 $\langle x \rangle$을 가지고 있습니다. $\langle x \rangle$은 $x$의 share를 의미하며 사용자가 $n$명이라고 할 때 $\langle x \rangle = {x_1, x_2, \dots, x_n }, \Sigma x_i = x$입니다. 계속 반복했던 이야기지만 검증자는 $n-1$개의 share만을 볼 수 있기 때문에 $x_i$로부터 $x$를 알아낼 수 없습니다.

먼저 상수 $a$를 $x$에 더하는 방법은 간단합니다. 1번 사용자만 자신의 $\langle x \rangle$에 $a$를 더하면 됩니다.

두 변수 $x$, $y$를 더하는 것 또한 $\langle x \rangle + \langle y \rangle$를 계산하면 끝입니다. 이 두 선형 연산은 사용자들 사이의 정보 교환을 필요로 하지 않고 독립적으로 수행할 수 있습니다.

그러나 곱셈은 그렇지가 않습니다. 두 변수 $x, y$가 있을 때 $z = x \cdot y$를 계산하는 과정은 아래와 같습니다.

1. 미리 $c = a \cdot b$를 만족하는 $a, b, c$를 정해 $\langle a \rangle , \langle b \rangle , \langle c \rangle$를 각 사용자가 나누어가집니다.

2. $\langle \alpha \rangle = \langle x-a \rangle, \langle \beta \rangle = \langle y-b \rangle$를 각 사용자가 계산한 후 그 결과를 공유합니다. 공유를 하고 나면 $\alpha, \beta$를 모든 사용자가 알 수 있습니다.

3. 각 사용자는 $\langle z \rangle = \langle c \rangle - \alpha \cdot \langle b \rangle - \beta \cdot \langle a \rangle + \alpha \cdot \beta$를 계산합니다.

이 과정이 올바른 $\langle z \rangle$를 생성한다는 사실은 $\Sigma z_i$를 계산해서 확인할 수 있습니다.

2번 과정을 보면 알 수 있듯 곱셈을 수행하기 위해서는 사용자들 사이에서의 정보 교환이 필요합니다.

곱셈 과정을 이해했다면 inverse 연산 또한 이해할 수 있습니다. 변수 $s$의 inverse를 게산하는 과정은 아래와 같습니다.

1. 임의의 변수 $r$을 정해 각 사용자는 $\langle r \rangle$을 나누어 가집니다.
2. 각 사용자는 $\langle s \cdot r \rangle$을 계산한 후 그 결과를 공유합니다. 공유를 하고 나면 $s \cdot r$을 모든 사용자가 알 수 있습니다.
3. 각 사용자는 $s^{-1} \cdot r^{-1}$을 계산합니다. 2번 과정에서 $s \cdot r$을 이미 공유했기 때문에 $s^{-1} \cdot r^{-1}$은 정보 교환 없이 알 수 있습니다.
4. $\langle s^{-1} \rangle = s^{-1} \cdot r^{-1} \cdot \langle r \rangle$입니다.

즉, $s^{-1} \cdot r^{-1}$을 나눠가진 후 $r$을 곱하는 방식으로 계산이 이루어집니다. 이렇게 계산할 경우 1개의 inverse 계산당 4개의 원소를 추가로 필요로 하게 됩니다.

이 방법을 통해 서명을 만들었을 때 이론적으로 추정한 서명 크기는 아래와 같습니다.

Boolean circuit에서는 서명의 크기가 52kB인 반면 Arithmetic circuit에서는 31.6kB으로 대략 40% 정도 크기를 줄였음을 알 수 있습니다. $L1$은 128비트 안전성을 의미합니다.

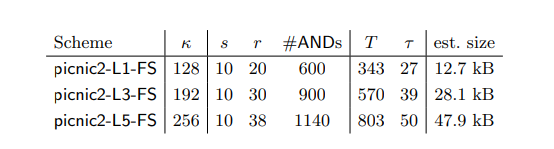
LowMC는 Security Level $L1$에서 서명의 크기가 12.7kB였던 것과 비교하면 결과에 아쉬운 점이 있지만 그럼에도 불구하고 처음 제시된 AES를 이용한 MPC라는 점에서 논문의 의의가 있습니다.

4. Banquet

Banquet은 BBQ보다 더 발전된 형태의 AES를 이용한 MPC-based 전자서명입니다.(논문 제목 : Banquet: Short and Fast Signatures from AES) 이론적인 아이디어를 제공했을 뿐만 아니라 실제 구현체를 제공해 실행 시간과 서명 크기를 확인해볼 수 있습니다.(구현체 링크)

Banquet에서는 각 사용자가 S-box를 직접 수행하는 대신(즉 입력 $x$의 inverse를 계산하는 대신) 그냥 S-box의 출력 $y$를 같이 줘서 $x \cdot y = 1$인지를 확인하게 한다는 아이디어를 제시했습니다.

이 아이디어를 사용한다면 곱셈에서는 미리 계산되어 $a \cdot b = c$를 만족하는 $\langle a \rangle, \langle b \rangle, \langle c \rangle$가 사용되므로 inverse 계산을 4개의 원소 대신 3개의 원소만을 사용해 처리할 수 있습니다.

S-box의 출력을 넘겨주면 Zero-knowledge 성질이 만족하지 않는게 아닌가 하는 의문이 들 수 있지만 여기서도 각 사용자는 masking된 값만을 들고 있기 떄문에 Zero-knowledge 성질이 잘 만족됩니다.

또한 여기서 더 나아가 Lagrange interpolation을 통해 여러 개의 곱셈을 한번에 수행하는 최적화를 사용하고 있습니다. AES에서 S-box가 $m$개 쓰인다고 하고 각 S-box의 입력을 $s_1, s_2, \dots , s_m$, 출력을 $t_1, t_2, \dots , t_m$이라고 하겠습니다.

그러면 우리는 $s_i \cdot t_i = 1$인지를 각 $i$에 대해 확인해야 합니다. 그런데 그 대신에 만약 $\Sigma s_i \cdot t_i = m$인지를 확인하면 어떨까요? 물론 이 방법은 False positive를 가지고 있습니다. 그러나 이 False positive는 동일한 과정을 반복 수행해서 낮출 수 있기 때문에 이렇게 한꺼번에 계산하는게 효율적이라면 충분히 도입할 여지가 있습니다.

Lagrange interpolation도 마찬가지의 원리를 사용합니다. 구체적으로 과정을 살펴보겠습니다.

1. 총 $m$개의 점 $(i, s_{i+1})$을 가지고 Lagrange interpolation을 수행해 degree $m$의 다항식 $S(x)$를 만들어냅니다. 이 때 하나의 점은 랜덤하게 추가합니다.

2. 총 $m$개의 점 $(i, t_{i+1})$을 가지고 Lagrange interpolation을 수행해 degree $m$의 다항식 $T(x)$를 만들어냅니다. 이 때 하나의 점은 랜덤하게 추가합니다.

3. $P = S \cdot T$를 계산합니다. $0 \leq x \leq m-1$에 대해 $P(x) = 1$을 만족하고 다른 $x$에 대해서는 $S(x) \cdot T(x) = P(x)$입니다.

4. 검증자가 선택한 $R$에 대해 $P(R) = S(R) \cdot T(R)$인지 계산해서 $P$가 올바르게 정해진게 맞는지 검증합니다.

증명자가 비밀키를 모른 상태로 증명을 위조한다는 의미는 적어도 어느 한 $i$에 대해서 $s_i \cdot t_i \neq 1$이라는 의미입니다. 그러면 이 절차를 그대로 따라갈 경우 $P(i) \neq 1$이기 때문에 검증자가 증명에 문제가 있음을 발각할 수 있습니다.

증명자는 검증자를 속이기 위해 $0 \leq x \leq m-1$에 대해 $P(x) = 1$을 만족하는 임의의 $P$를 제시하고 검증자가 선택한 $R$에 대해 $P(R) = S(R) \cdot T(R)$이 만족하기를 기도하는 방법이 있습니다. $P - S \cdot T$는 $2m$차 다항식이기 때문에 $P(R) = S(R) \cdot T(R)$을 만족하는 $R$은 $2m$개가 있다고 알 수 있고, $GF(2^8)$ 위에서 계산을 할 경우 soundness error는 $2m / 2^8$으로 상당히 높게 됩니다. 그렇기 때문에 적당히 큰 $\lambda$를 골라 원소를 $GF(2^{8\lambda})$ 위로 보내버립니다. 이렇게 되면 soundness error는$2m / 2^{8 \lambda}$로 줄어들게 됩니다.

복잡해서 자세하게 소개는 하지 않겠지만, 여기서 추가적인 최적화로 Lagrange Interpolation을 한 번 써서 $2m$차 다항식으로 계산하는 대신 Lagrange Interpolation을 $\sqrt{m}$번 써서 $2\sqrt{m}$차 다항식 $\sqrt{m}$개를 얻은 후, 다항식 $\sqrt{m}$개의 합을 가지고 계산을 수행합니다. 이 최적화를 거치고 나면 1개의 S-box당 4바이트 = 32비트의 공간을 사용하던 BBQ와 달리 6.5비트를 사용하도록 만들 수 있습니다.

Banquet을 이용한 전자서명과, LowMC를 이용한 Picnic과, 해시를 이용한 SPHINCS+의 성능을 비교한 표는 아래와 같습니다.(SPHINCS는 MPC 없이 순수하게 해시만을 이용한 전자서명입니다.)

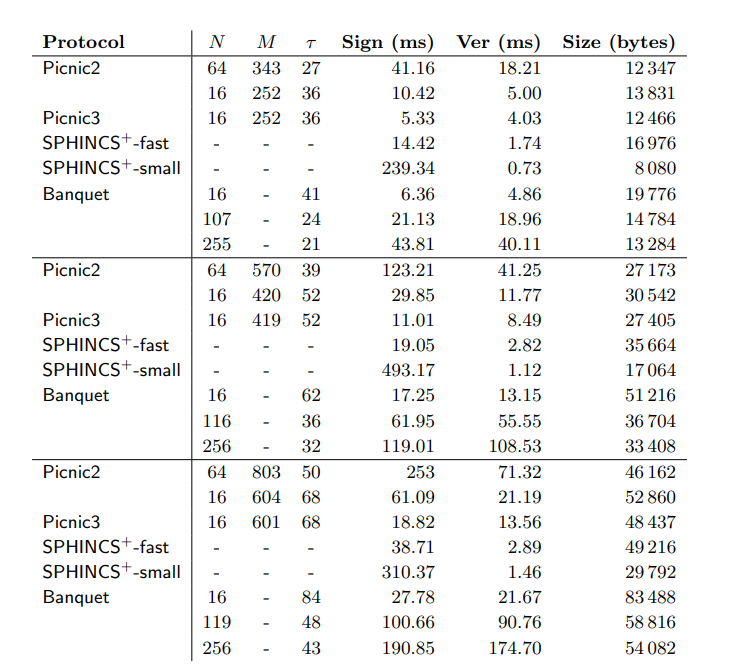
결과를 확인해보면 Picnic에 비해 성능이 조금 부족한 것은 사실이나 AES와 LowMC의 차이를 생각해볼 때 안전성과 이 정도의 성능 trade-off는 충분히 합리적인 정도까지 발전이 이루어졌습니다. 구체적으로 서명/검증 속도가 비슷할 때 크기가 1.5배 정도 증가하고, 크기가 비슷할 때 서명/검증 속도가 10배 정도 증가하는 정도로 BBQ에 비해 상당히 개선이 이루어진 것을 확인할 수 있습니다.

5. Conclusions

이번 글에서는 AES를 이용하는 두 전자서명 구조를 확인해보았습니다. 기본적으로 inverse 연산은 비용이 큰 연산이고, 원래 AES를 계산할 때에도 이 연산은 lookup table로 처리합니다.

그런데 MPC에서는 여러 테크닉을 통해 inverse를 다소 효율적으로 처리할 수 있고 특히 soundness error를 줄이기 위해서는 inverse가 이루어지는 필드의 차수가 클 수록 이득일 수 있는 상황입니다.

아직 자세히 보지는 않았지만 MPC를 효율적으로 하기 위해 아예 AES를 $GF(2^8)$이 아니라 $GF(2^{32})$에서 수행하는 Rainier라는 전자서명도 최근에 제안된 바가 있는 만큼 검증된 AES 구조를 통한 MPC의 발전 가능성은 더욱 커보입니다.