Expected Complexity of Random Convex Hulls
Table Of Contents
Introduction
안녕하세요, Aeren입니다!
Convex hull은 computational geometry의 가장 기본이 되는 개념 중 하나입니다. 이번 글에서는 $\mathbb{R} ^ 2$의 compact (closed and bounded와 동치입니다.) and convex subset에서 uniformly random하게 선택된 점들의 집합의 convex hull의 vertex의 갯수의 기댓값을 알아볼 것입니다.
이 글은 다음 글을 바탕으로 작성되었습니다.
Experimental Results
다음은 $C$가 unit disk, unit triangle, unit square일때 100회의 sampling으로 얻어낸 convex hull의 평균 vertex 갯수입니다.
| $n$ \ $C$ | Unit Disk | Unit Triangle | Unit Square |
|---|---|---|---|
| $2^{10}=1024$ | 33.64 | 14.72 | 17.65 |
| $2^{11}=2048$ | 42.98 | 16.45 | 20.1 |
| $2^{12}=4096$ | 53.67 | 17.52 | 22.3 |
| $2^{13}=8192$ | 68.16 | 19.02 | 23.69 |
| $2^{14}=16384$ | 86.08 | 20.8 | 25.66 |
| $2^{15}=32768$ | 108.78 | 22.03 | 27.37 |
| $2^{16}=65536$ | 137.32 | 23.44 | 28.76 |
Unit disk의 경우 $n$이 8배 증가할 때마다 평균이 약 2배정도 늘어나고, unit triangle과 unit square의 경우 linear하게 증가하는 것으로 보아, 각각 $O(\sqrt[3]{n}), O(\log n), O(\log n)$정도임을 추측해 볼 수 있습니다.
다음은 위 데이터를 얻어내는데 사용한 C++ 코드입니다.
#include <bits/stdc++.h>
using namespace std;
template<class T>
struct point{
T x{}, y{};
point(){ }
template<class U> point(const point<U> &otr): x(otr.x), y(otr.y){ }
template<class U, class V> point(U x, V y): x(x), y(y){ }
template<class U> explicit operator point<U>() const{ return point<U>(static_cast<U>(x), static_cast<U>(y)); }
T operator*(const point &otr) const{ return x * otr.x + y * otr.y; }
T operator^(const point &otr) const{ return x * otr.y - y * otr.x; }
point operator+(const point &otr) const{ return {x + otr.x, y + otr.y}; }
point &operator+=(const point &otr){ return *this = *this + otr; }
point operator-(const point &otr) const{ return {x - otr.x, y - otr.y}; }
point &operator-=(const point &otr){ return *this = *this - otr; }
point operator-() const{ return {-x, -y}; }
#define scalarop_l(op) friend point operator op(const T &c, const point &p){ return {c op p.x, c op p.y}; }
scalarop_l(+) scalarop_l(-) scalarop_l(*) scalarop_l(/)
#define scalarop_r(op) point operator op(const T &c) const{ return {x op c, y op c}; }
scalarop_r(+) scalarop_r(-) scalarop_r(*) scalarop_r(/)
#define scalarapply(op) point &operator op(const T &c){ return *this = *this op c; }
scalarapply(+=) scalarapply(-=) scalarapply(*=) scalarapply(/=)
#define compareop(op) bool operator op(const point &otr) const{ return tie(x, y) op tie(otr.x, otr.y); }
compareop(>) compareop(<) compareop(>=) compareop(<=) compareop(==) compareop(!=)
#undef scalarop_l
#undef scalarop_r
#undef scalarapply
#undef compareop
T squared_norm() const{ return x * x + y * y; }
};
template<class T, class U, class V>
T doubled_signed_area(const point<T> &p, const point<U> &q, const point<V> &r){
return q - p ^ r - p;
}
using pointd = point<double>;
// Requires point
template<class T>
struct line{
point<T> p{}, d{}; // p + d*t
line(){ }
line(point<T> p, point<T> q): p(p), d(q - p){ }
operator bool() const{ return d.x != 0 || d.y != 0; }
};
template<class T>
point<double> projection(const point<T> &p, const line<T> &L){
return static_cast<point<double>>(L.p) + (L ? (p - L.p) * L.d / L.d.squared_norm() * static_cast<point<double>>(L.d) : point<double>());
}
template<class T>
point<double> reflection(const point<T> &p, const line<T> &L){
return 2.0 * projection(p, L) - static_cast<point<double>>(p);
}
using lined = line<double>;
// type {0: both, 1: lower, 2: upper}
template<class T, int type = 0>
struct convex_hull{ // (Lower, Upper) type {0: both, 1: lower, 2: upper}
vector<point<T>> lower, upper;
convex_hull(vector<point<T>> arr = {}, bool is_sorted = false){
if(!is_sorted) sort(arr.begin(), arr.end()), arr.erase(unique(arr.begin(), arr.end()), arr.end());;
#define ADDP(C, cmp) while((int)C.size() > 1 && doubled_signed_area(C[(int)C.size() - 2], p, C.back()) cmp 0) C.pop_back(); C.push_back(p);
for(auto &p: arr){
if(type < 2){ ADDP(lower, >=) }
if(!(type & 1)){ ADDP(upper, <=) }
}
#undef ADDP
reverse(upper.begin(), upper.end());
}
vector<point<T>> get_hull() const{
if(type) return type == 1 ? lower : upper;
if((int)lower.size() <= 1) return lower;
vector<point<T>> res(lower);
res.insert(res.end(), ++ upper.begin(), -- upper.end());
return res;
}
};
int main(){
auto find_average_size = [&](int n, auto random_point_generator, int repetition)->double{
double sum = 0;
for(auto rep = 0; rep < repetition; ++ rep){
vector<pointd> S(n);
generate(S.begin(), S.end(), random_point_generator);
sum += (int)convex_hull(S).get_hull().size();
}
return sum / repetition;
};
mt19937 rng(1564);
auto generate_from_unit_disk = [&]()->pointd{
static uniform_real_distribution<double> gen_r(0, 1);
static uniform_real_distribution<double> gen_theta(0, 2 * acos(-1));
double r = sqrt(max(gen_r(rng), 0.0)), theta = gen_theta(rng);
return {r * cos(theta), r * sin(theta)};
};
auto generate_from_unit_triangle = [&]()->pointd{
static uniform_real_distribution<double> gen_l(0, 1);
static const pointd A{1, 0}, B{1.0 / 2, sqrt(3) / 2};
pointd p = gen_l(rng) * A + gen_l(rng) * B;
if(doubled_signed_area(A, B, p) < 0){
p = reflection(p, lined(A, B));
}
return p;
};
auto generate_from_unit_square = [&]()->pointd{
static uniform_real_distribution<double> gen_l(0, 1);
return {gen_l(rng), gen_l(rng)};
};
for(auto n: {1 << 10, 1 << 11, 1 << 12, 1 << 13, 1 << 14, 1 << 15, 1 << 16}){
cout << "n = " << n << "\n ";
cout << find_average_size(n, generate_from_unit_disk, 100) << " ";
cout << find_average_size(n, generate_from_unit_triangle, 100) << " ";
cout << find_average_size(n, generate_from_unit_square, 100) << endl;
}
return 0;
}
Notations
$\mathbb{R} ^ 2$의 고정된 compact and convex subset $C$이 주어졌을 때,
- $S \subseteq \mathbb{R}^2$에 대하여 $CH(S)$를 $S$의 convex hull,
- $P _ n$을 $C$로부터 uniformly random하게 sample된 $n$개의 점들의 집합에 대응되는 random variable,
- $A _ n$을 $CH(X _ n)$의 area에 대응 되는 random variable, 그리고
- $V _ n$을 $CH(P _ n)$의 vertex의 갯수에 대응 되는 random variable이라 하겠습니다.
Planar Case
위의 추측들을 증명하기에 앞서 하나의 lemma를 증명하겠습니다.
LEMMA (Area-to-vertex Lemma)
어떤 함수 $f:\mathbb{Z} _ {> 0} \rightarrow [0,1]$가 존재하여, 모든 $n \in \mathbb{Z} _ {> 0}$에 대해 $E \left[ A _ n \right] \ge (1-f(n)) \cdot Area(C)$이라면, $E \left[ V _ n \right] \le n \cdot f(n/2)$이다.
이 lemma는 convex hull의 바깥쪽의 넓이의 기댓값이 클수록 convex hull의 vertex갯수의 기댓값이 큼을 의미합니다.
PROOF
$L _ n$을 $P _ n$에서 처음 $n/2$개의 점, $R _ n$을 마지막 $n/2$개의 점을 나타내는 random variable이라 합시다. 또한 $VL _ n$을 $CH(P _ n)$의 vertex를 이루는 $L _ n$의 원소의 갯수, 그리고 $VR _ n$을 $CH(P _ n)$의 vertex를 이루는 $R _ n$의 원소의 갯수를 나타내는 random variable이라 합시다.
먼저, 정의에 의해, $E \left[ V _ n \right] = E \left[ VL _ n \right] + E \left[ VR _ n \right]$입니다.
이제 $R _ n$을 고정시켜봅니다. $L _ n$의 각 원소가 $CH(P _ n)$의 vertex를 이룰려면 최소한 $CH(R _ n)$의 외부에 위치해야 합니다. 즉, 다음 inequality가 성립합니다.
$\begin{align} E \left[ VL _ n \vert R _ n \right] \le \frac{n}{2} \cdot \frac{Area(C)-Area(CH(R _ n))}{Area(C)} \end{align}$
임의의 두 real random variable $X$와 $Y$에 대하여, $E \left[ X \right] = E \left[ E \left[ X \vert Y \right] \right]$가 성립하므로, 다음을 얻어낼 수 있습니다.
$\begin{align} E \left[ VL _ n \right] & = E \left[ E \left[ VL _ n \vert R _ n \right] \right] \newline & \le E \left[ \frac{n}{2} \cdot \frac{Area(C)-Area(CH(R _ n))}{Area(C)} \right] \newline & = \frac{n}{2} \cdot \frac{Area(C)- E \left[ Area(CH(R _ n)) \right] }{Area(C)} \newline & \le \frac{n}{2} \cdot f\left(\frac{n}{2} \right) \end{align}$
$E \left[ VL _ n \right]$에 대해서도 같은 부등식이 성립하므로 두 식을 더하면 다음이 얻어집니다.
$E \left[ V _ n \right] = E \left[ VL _ n \right] + E \left[ VR _ n \right] \le n \cdot f(n/2)$
$\blacksquare$
이제 처음 관찰들을 증명할 준비가 되었습니다.
THEOREM
$C$가 unit disk일 때, $E \left[ V _ n \right] \in O(n ^ {1/3})$이다.
PROOF
$E \left[ \pi - A _ n \right] \in O(n ^ {-2/3})$임을 보이면 area-to-vertex lemma에 의해 본 theorem이 증명됩니다.
일반성을 잃지 않고 어떤 positive integer $m$에 대하여 $n=m ^ 3$이라 가정합시다.
$C$의 둘레에 $m$개의 점을 균일한 간격으로 찍고 중심과 연결하여 $m$개의 영역 $S _ 1, …, S _ m$으로 분할하겠습니다.
또한 $C$와 중심이 같은 disk $C _ 1, …, C _ {m ^ 2}$를 $C _ 1 = C$ 그리고 $Area(C _ {i - 1})=Area(C _ i) + \pi / {m ^ 2}$이 성립하도록 정의하고 $C _ i$의 반지름을 $r _ i$라 하겠습니다.
그리고 $i = 1, \cdots, m ^ 2 - 1, j = 1, \cdots, m$에 대해, $S _ {i, j} = (C _ i - C _ {i + 1}) \cap S _ j$, $S _ {m ^ 2, j} = C _ {m ^ 2} \cap S _ j$라 놓겠습니다. $S _ {i, j}$는 $S _ j$의 tile이라 부르겠습니다.
각 $j = 1, \cdots, m$에 대해, $X _ j$를 $P _ n \cap S _ {i, j} \ne \emptyset$인 최소의 $i$를 나타내는 probability variable이라 합시다. 고정된 $j$에 대해, $X _ j = k$일 확률은 $S _ {1, j}, \cdots, S _ {k - 1, j}$가 $P _ n$의 점을 포함하지 않을 확률보다 작거나 같습니다. 즉,
$\begin{align} P \left[ X _ j = k \right] \le \left( 1 - \frac{k - 1}{n} \right) ^ n \le e ^ {-k + 1} \end{align}$
이 성립합니다. 따라서
$\begin{align} E \left[ X _ j \right] = \sum _ {k = 1} ^ {m ^ 2} k \cdot P \left[ X _ j = k \right] \le \sum _ {k = 1} ^ {m ^ 2} k \cdot e ^ {-k + 1} \in O(1) \end{align}$
을 얻어낼 수 있습니다.
$S _ {i, j}$가 집합 $T \subseteq \mathbb{R} ^ 2$에 의해 expose되었다는 것을 $S _ {i, j} - T \ne \emptyset$이 성립하는 것이라 정의합시다.
또한 원점 $o$에 대해, $H _ o = CH(P _ n \cup \lbrace o \rbrace)$라 놓겠습니다.
그리고 고정된 $j = 1, \cdots, m$에 대해서 $k = \max( X _ {j - 1}, X _ {j + 1} )$라 놓고 (여기서 $X _ 0 = X _ m, X _ {m + 1} = X _ 1$로 취급합니다), $p$와 $q$를 삼각형 $T = \Delta opq$에 의해 expose된 $S _ j$의 집합들의 갯수를 최대화시키도록 $S _ {j - 1}$과 $S _ {j + 1}$에서 각각 뽑은 점이라고 합시다. 다음 figure와 같이 $p$와 $q$가 $S _ {k + 1}$의 boundary에 놓이면서 $S _ {j - 1}, S _ j, S _ {j + 1}$을 감싸는 $C$의 반지름 위에 놓이도록 할 수 있습니다.
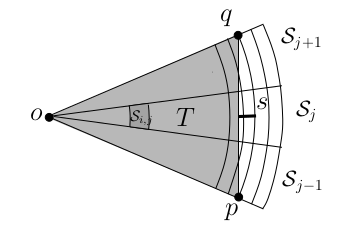
$H _ o$에 의해 expose된 $S _ j$의 tile의 갯수는 자명하게 $T$에 의해 expose된 $S _ j$의 tile의 갯수보다 크거나 같습니다.
$s$를 선분 $pq$의 중점과 $C _ k$의 boundary 위의 가장 가까운 점을 이은 선분이라고 합시다.
$T$에 의해 expose된 $S _ j$의 tile의 갯수는 $\max(X _ {j - 1}, X _ {j + 1})$과 $s$와 만나는 tile의 갯수의 합으로 bound되어있습니다.
$s$의 길이는
$\begin{align} \vert oq \vert \cdot \left(1 - \cos{\frac{3\pi}{m}} \right) \le 1 - \cos{\frac{3\pi}{m}} \le \frac{9\pi ^ 2}{2 m ^ 2} \end{align}$
을 만족합니다.
한편, $r _ {i + 1} - r _ i \ge 1 / 2 m ^ 2$을 만족하므로, 선분 $s$는 최대 $ \left( 9\pi ^ 2 / 2m^2 \right) / \left( 1 / m ^ 2 \right) \le 89$개의 tile들과 만납니다.
따라서 $H _ o$에 의해 expose된 tile의 갯수 $Z$는 다음 값에 의해 bound되어 있습니다.
$Z \le \begin{align} E \left[ \sum_{i=1}^m \left( X _ {j-1} + X _ {j+1} + 89 \right) \right] \in O(m) \end{align}$
$H=CH(N)$의 넓이는 $H$에 의해서 expose되어있지 않은 tile들의 넓이의 합으로 작은쪽에서 bound되어 있습니다. 또한 $H$가 $o$를 포함하지 않을 확률은 자명하게 $2 \pi / 2 ^ n$이하입니다. 따라서
$\begin{align} E\left[ \pi - Area(H) \right] \le \pi - E\left[ Area(H _ o) - P\left[ H \ne H _ o \right] \cdot \pi \right] \le E \left[ Z \right] \cdot \frac\pi n + \frac{2 \pi ^ 2}{2 ^ n} \end{align} \in O(n ^ {-2/3})$
가 성립하므로 area-to-vertex lemma에 의해 본 theorem의 증명이 완료됩니다.
$\blacksquare$
THEOREM
$C$가 (내부를 포함하는) unit square일 때, $E \left[ V _ n \right] \in O(\log n)$이다.
PROOF
$E \left[ 1 - A _ n \right] \in O(\log n / n)$임을 보이면 area-to-vertex lemma에 의해 본 theorem이 증명됩니다.
$C$를 $n$개의 행과 $n$개의 열로 이루어진 넓이가 같은 $n ^ 2$개의 square로 분할합니다. 이 때 $S _ {i, j}$를 $i$번째 행, $j$번째 열의 square, $S _ i = \cup _ {j = 1} ^ m S _ {i, j}$, 그리고 $S \left( l, r \right) = \cup _ {i=l} ^ r S _ i$라고 합시다. 또한 $X _ j$를 $S(1, j - 1)$의 row중 $P _ n$의 점을 포함하는 index가 가장 작은 row의 index라고 하고, $X’ _ j$를 $S(j + 1, n)$의 row중 $P _ n$의 점을 포함하는 index가 가장 작은 row의 index라고 합시다. 대칭성에 의해, $E \left[ X _ j \right] = E \left[ X’ _ {n - j + 1} \right]$이 모든 $j=2, \cdots, n - 1$에 대해 성립합니다.
$Z _ j$를 $j$번째 열의 아래쪽에서 $CH(P _ n)$에 의해 expose된 tile의 갯수라고 정의합시다. Unit disk에서와 마찬가지 논증으로 $Z _ j \le X _ j + X ‘ _ j$를 얻어낼 수 있습니다. 따라서 $E \left[ Z _ j \right]$를 bound시키기 위해 먼저 다음 figure와 같이 $S(1,j-1), S(j+1, n)$을 넓이 $1/n$이상인 tile들로 덮겠습니다.
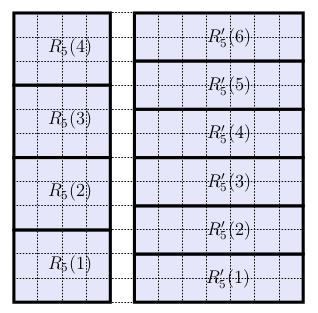
$h(l) = \lceil n / (l - 1) \rceil$, $R _ j(m) = \left[ 0, (j - 1)/n \right] \times \left[ h(n-j+1)(m-1)/n, h(j)m/n \right]$, $R’ _ j (m) = \left[ (j+1)/n, 1 \right] \times \left[ h(j)(m-1)/n, h(j)m/n \right]$이라 놓고, $Y _ j$를 $R _ j(i) \cap P _ n \ne \emptyset$를 만족하는 최소의 index $i$라고 정의하겠습니다.
$R _ j(i)$의 넓이는 $1/n$이상이므로, Unit disk에서와 마찬가지 논증으로 $E \left[ Y _ j \right] \in O(1)$을 얻을 수 있습니다. 또한, $E \left[ X _ j \right] \le h(j) \cdot E \left[ Y _ j \right] \in O(n / (j - 1))$이며, 대칭적으로 $E \left[ X’ _ j \right] \in O(n / (n - j))$입니다.
이제, 지금까지의 논증을 남은 3방향 (왼쪽, 오른쪽, 위)에 대해 반복해준뒤 더해주면, $CH(P _ n)$에 의해 expose된 tile들의 갯수의 기댓값은
$\begin{align} 4n - 4 + 4 \sum _ {j = 2} ^ {n - 1} E \left[ Z _ j \right] < 4n + 4 \sum _ {j = 2} ^ {n - 1} \left( E \left[ X _ j \right] + E \left[ X’ _ j \right] \right) \in O\left(4n + 8 \sum _ {j = 2} ^ {n - 1} \frac{n}{j - 1} \right) = O(n \log n) \end{align}$
에 bound됨을 알 수 있습니다.
각 tile의 넓이는 $1/n^2$이므로, $E \left[ 1 - A _ n \right]\in O(\log n / n)$이 얻어집니다.
$\blacksquare$
THEOREM
$C$가 (내부를 포함하는) triangle일 때, $E \left[ V _ n \right] \in O(\log n)$이다.
PROOF
$E \left[ 1 - A _ n / Area(C) \right] \in O(\log n / n)$임을 보이면 area-to-vertex lemma에 의해 본 theorem이 증명됩니다.
다음 figure와 같이 $C$를 $n ^ 2$개의 동일한 넓이의 영역으로 분할하겠습니다.
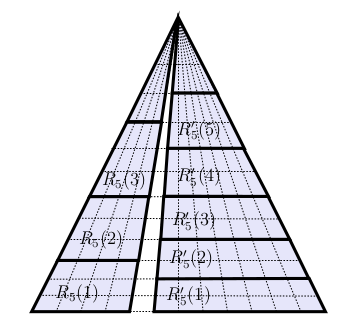
먼저 vertex 하나를 고정하고, 반대편 segment를 $n$등분하여 $n-1$개의 점들과 연결해줍니다. 그리고, 그 segment와 평행한 선분 $n-1$개를 나눠진 영역의 넓이가 같도록 추가합니다.
이렇게 분할된 영역은 unit square일 때와 완전히 같은 논증으로 같은 bound를 얻어낼 수 있습니다. 이를 세 방향 모두 반복해 준 후 더해주면, 원하는 area의 bound를 얻어낼 수 있습니다.
$\blacksquare$
다음 theorem은 triangle, square뿐만 아니라 arbitrary convex polygon에 대해서 $E \left[ V _ n \right]$의 complexity에 대해 알려줍니다.
THEOREM
$C$가 convex $k$-gon일 때, $E \left[ V _ n \right] \in O(k \log n)$이다.
$C$의 임의의 triangulation $C _ 1, \cdots, C _ {k - 2}$를 잡겠습니다. 또한 $Y _ i = \vert C _ i \cap P _ n \vert $, $Q _ i = C _ i \cap P _ n$, 그리고 $Z _ i = \vert CH(C _ i) \vert $라 놓겠습니다.
$T _ i$안에서 $Q _ i$의 점들의 분포는 $Y _ i$개의 점들을 uniformly random하게 뽑았을 때의 분포와 동일합니다. 따라서, 바로 위의 theorem에 의해, $E \left[ Z _ i \vert Y _ i \right] = E \left[ E \left[ Z _ i \vert Y _ i \right] \right] \in O(E \left[ \log Y _ i \right]) = O(\log n)$입니다. 이제 모든 $i$에 대해서 더해주면
$\begin{align} E \left[ V _ n \right] \le E \left[ \sum _ {i = 1} ^ {k - 2} \vert CH(C _ i) \vert \right] \le \sum _ {i = 1} ^ {k - 2} E \left[ Z _ i \right] \in O(k \log n) \end{align}$
을 얻어낼 수 있습니다.
$\blacksquare$
On Higher Dimension
위의 Area-to-vertex lemma는 더 높은 dimension에서 hypervolume-to-vertex lemma로 확장할 수 있습니다. (증명 과정도 완전히 동일합니다.) 이를 이용해 다음 결과를 얻어낼 수 있습니다. 이의 증명은 생략하도록 하겠습니다.
THEOREM
$C$가 $\mathbb{R} ^ d$의 unit hypercube일 때, $CH(C)$의 vertex의 갯수의 기댓값은 $O(\log ^ {d - 1} n)$이다.
Summary
| Region Type | $E \left[ V _ n \right]$ |
|---|---|
| Disk | $O(n ^ {1/3})$ |
| Convex $k$-gon | $O ( k \log n)$ |
| $d$-dimensional hypercube | $O(\log ^ {d - 1} n)$ |