Persistent Data Structures
Persistent Introduction
과거의 상태를 보존하는 자료구조를 persistent data structure라고 합니다. 예를 들어, persistent array는 과거의 배열의 상태를 담고 있는 “버전”을 갖고 있습니다. 여기에 “버전 $x$에서 $i$번째 원소를 $d$로 바꿔서 버전 $y$를 만들어라”, 또는 “버전 $x$에서 $i$번째 원소의 값을 반환해라” 등의 연산을 적용할 수 있습니다.
Persistent segment tree(PST)에 대한 자료는 인터넷에서 많이 찾아볼 수 있습니다. 하지만 persistence라는 개념은 segment tree에만 적용되는 것이 아닙니다. PST는 persistence를 지원하는 일반적인 방법을 segment tree에 적용한 것일 뿐, segment tree만을 위한 특별한 아이디어를 적용해서 만든 것이 아닙니다.
이 글에서는 수많은 자료구조를 기계적이고 간단한 방법을 통해 persistent data structure로 바꿀 수 있다는 것을 보이고자 합니다.
Persistent Stack
Linked list로 구현한 평범한 스택을 생각해 봅시다. 각각의 노드에는 고유의 값이 쓰여 있고, 다른 노드를 가리키는 포인터를 갖고 있습니다.
struct Node{
int v;
Node *nxt;
Node(int V, Node *N): v(V), nxt(N) {}
};
struct Stack{
Node *head = NULL;
void push(int v){
head = new Node(v, head);
}
int top(){
assert(head);
return head->v;
}
void pop(){
assert(head);
head = head->nxt;
}
};
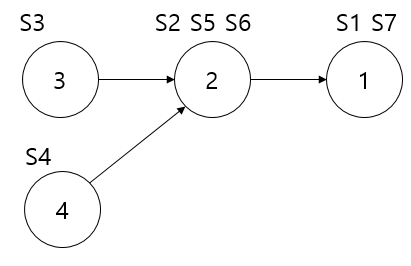
일반적인 스택에서는 push나 pop을 하면 머리 노드가 바뀌고, 기존의 머리 노드에 대한 정보는 사라집니다. 이 정보를 버리지 말고, $i$번째 연산을 하기 직전의 머리 노드 $S_i$를 모두 저장해 봅시다. 그러면 아래처럼 같은 $S_2$에 다른 원소를 push하여 $S_3$와 $S_4$를 만들 수도 있고, 이전 버전인 $S_1$의 맨 앞 원소가 얼마인지도 알 수 있습니다.
struct Node{
int v;
Node *nxt;
Node(int V, Node *N): v(V), nxt(N) {}
};
struct Stack{
Node *head;
Stack(): head(NULL) {}
Stack(Node *N): head(N) {}
Stack *push(int v){
return new Stack(new Node(v, head));
}
int top(){
assert(head);
return head->v;
}
Stack *pop(){
assert(head);
return new Stack(head->nxt);
}
};
int main(){
Stack *S = new Stack;
Stack *S1 = S->push(1);
Stack *S2 = S1->push(2);
Stack *S3 = S2->push(3);
cout << S2->top(); // 2
Stack *S4 = S2->push(4);
cout << S3->top(); // 3
cout << S4->top(); // 4
Stack *S5 = S4->pop();
cout << S5->top(); // 2
Stack *S6 = S3->pop();
cout << S2->top(); // 2
Stack *S7 = S6->pop();
cout << S7->top(); // 1
}
만약 “머리의 값을 $v$로 바꾼다”라는 연산을 지원하면 어떻게 될까요? 기존의 스택이라면 그냥 바꾸면 되겠지만, persistent stack에서 그러면 이전 버전이 보존되지 않아서 안 됩니다. 그 대신 머리를 그대로 복사한 다음, 그 복사본의 값을 $v$로 바꿔야 합니다. 포인터는 복사한 그대로 남아있으므로 두 번째 노드를 가리키고 있을 것입니다. 그리고 스택의 버전이 바뀌었으므로 이 연산에서 새로운 머리를 반환해줍시다.
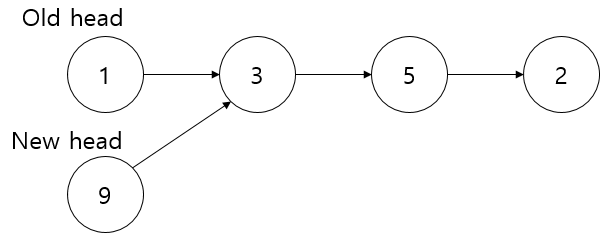
struct Node{
// ... (중략) ...
Node *copy(){
return new Node(v, nxt);
}
};
struct Stack{
// ... (중략) ...
Stack *change_head(int v){
assert(head);
Stack *s = new Stack(head->copy());
s->head->v = v;
return s;
}
};
그 다음으로, “두 번째 노드의 값을 $v$로 바꾼다”라는 연산을 지원하면 어떻게 될까요? 마찬가지로 두 번째 노드를 복사한 다음, 그 복사본의 값을 $v$로 바꾸면 됩니다.
그런데 이 연산에서 반환해줄 새로운 머리가 없습니다. 그렇다고 기존의 머리를 반환하면 안 됩니다. 그 머리는 이전 버전에 해당되고, 새로운 노드가 아닌 과거의 노드를 가리키고 있기 때문입니다. 따라서 머리도 새로 복사해 준 다음, 새 머리의 포인터도 바꿔주고 그 머리를 반환해야 합니다.
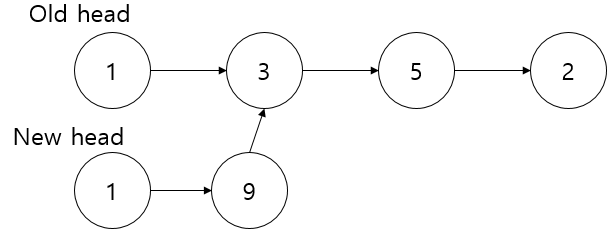
Stack *change_second(int v){
assert(head && head->nxt);
Node *n2 = head->nxt->copy();
n2->v = v;
Node *n1 = head->copy();
n1->nxt = n2;
return new Stack(n1);
}
마찬가지로, “$k$번째 노드의 값을 $v$로 바꾼다”라는 연산을 지원하려면 머리부터 $k$번째 노드까지 모두 복사해 주면 됩니다. 코드는 생략합니다.
Persistent Data Structures
위의 예시를 일반화해 봅시다. 다음 조건을 만족하는 자료구조를 생각합시다.
- 각 노드는 값과 포인터 필드로 이루어져 있습니다. (위의
Node::v와Node::nxt) - 자료구조 자체도 값과 포인터 필드로 이루어져 있습니다. (위의
Stack::head)
그러면 이 자료구조에서 일어나는 연산을 persistent하게 수행할 수 있습니다.
- 연산이 노드 몇 개의 필드를 수정할 텐데, 그렇게 수정되는 노드의 집합을 $N$이라고 합시다.
- 포인터를 통해 $N$의 노드 중 적어도 하나에 도달할 수 있는 노드의 집합을 $S$라고 합시다.
- $S$의 모든 노드를 복사하고, 자료구조 자체도 복사합니다. 노드 $x$를 복사한 것을 $x’$이라고 합시다.
- 복사된 모든 노드에 대해, 포인터가 $S$ 중 한 노드인 $y$를 가리키면 $y’$으로 바꿉니다. 복사된 자료구조에 대해서도, 포인터가 $S$ 중 한 노드를 가리키면 복사본으로 바꿉니다.
- 복사된 자료구조에 대해 기존의 연산을 적용합니다.
- 복사된 자료구조를 반환합니다.
특히 포인터들이 트리의 형태를 이루고 있고 $N$의 크기가 1이라면, $S$는 하나의 경로를 이룰 것입니다. 그래서 이 기법을 path copying이라고 부릅니다.
물론 정확히 이 순서로 복사, 수정할 필요는 없고, 순서만 잘 맞으면 됩니다. 예를 들어 특정 포인터 필드를 복사본으로 바꾸려면 먼저 그 복사본을 만들어야겠죠. 시간 복잡도는 복사된 노드의 크기(필드의 개수)의 합에 비례합니다.
위의 change_second를 예로 들어보면,
- $N$은 두 번째 노드 하나로 이루어져 있습니다.
- $S$는 첫 번째와 두 번째 노드로 이루어져 있습니다.
- $O(1)$ 크기의 노드 $O(1)$개를 복사했으므로, 시간 복잡도는 $O(1)$입니다.
Persistent Tree
트리를 persistent하게 바꿔봅시다. 만약 아래 그림에서 파란색 노드를 수정하려고 한다면, 복사해야 하는 노드는 파란색과 빨간색 노드입니다.

재귀 호출을 하면서 한 단계씩 내려가고, 재귀 호출이 반환한 복사본을 현재 노드의 포인터 필드에 넣으면 구현하기 쉽습니다. 아래 코드에 이 방식으로 binary search tree에 값을 추가하는 연산을 구현하였습니다. 시간 복잡도는 트리의 높이에 비례합니다.
struct Node{
int v;
Node *l, *r;
Node(int V, Node *L, Node *R): v(V), l(L), r(R) {}
Node *copy(){
return new Node(v, l, r);
}
Node *insert(int k){
Node *n = copy();
if(k < v){
if(!n->l) n->l = new Node(k, NULL, NULL);
else n->l = n->l->insert(k);
}
else{ // k > v
if(!n->r) n->r = new Node(k, NULL, NULL);
else n->r = n->r->insert(k);
}
return n;
}
bool search(int k){
if(k == v) return true;
if(k < v && l) return l->search(k);
if(k > v && r) return r->search(k);
return false;
}
};
Persistent Segment Tree
세그먼트 트리는 balanced binary tree의 형태를 띠고 있습니다. 그래서 persistent tree를 조금만 변형하면 persistent segment tree가 됩니다. 다음 두 가지만 추가하면 됩니다.
- 각 노드마다 그 서브트리의 크기를 저장합니다.
- 재귀를 사용하여 점 업데이트 연산을 구현합니다. 위의 persistent BST에서 봤던 대로, 왼쪽 또는 오른쪽 서브트리에 재귀 호출을 하고, 포인터를 그 호출이 반환한 복사본으로 바꿔치면 됩니다.
- 재귀를 사용하여 구간 쿼리 연산을 구현합니다. 각 서브트리의 크기를 알고 있으므로 노드, $l$, $r$만 피연산자로 사용하면 됩니다.
Persistent Array
우리가 흔히 쓰는 형태의 배열을 그대로 persistent하게 만드는 건 의미가 없습니다. 그냥 배열을 통째로 복사하는 거나 마찬가지니까요. 하지만 persistent array를 다른 방법으로 구현할 수는 있습니다. 그냥 persistent segment tree와 똑같이 구현하되, 구간 합 쿼리 대신 점 쿼리를 구현해 주고, 업데이트 후에 값을 합체하는 과정을 없애면 됩니다.
각 연산의 시간 복잡도는 $O(\log N)$입니다.
꼭 이진 트리일 필요는 없고, $K$진 트리를 만들어서 깊이를 줄이는 대신 노드의 크기를 늘릴 수도 있습니다.
Persistent Queue
Linked list 형태의 큐를 그대로 persistent하게 만드는 건 의미가 없습니다. $S$가 노드 전체의 집합이 되어 버리기 때문에, 큐를 통째로 복사하는 거나 마찬가지니까요. 하지만 array 형태의 큐도 있죠? Array는 persistent하게 만들 수 있음을 위에서 보았으니, 이걸 그대로 사용해서 persistent queue를 만들 수 있습니다. 마찬가지로 각 연산의 시간 복잡도는 $O(\log N)$입니다.
Persistent Union-find
Union-find를 배열 두 개로 구현할 수 있으므로, persistent union-find는 persistent array 두 개로 구현할 수 있습니다.
주의할 점은 path compression을 쓰면 안 된다는 것입니다. 왜냐하면 persistence를 추가하면 amortized analysis가 깨지기 때문입니다. Amortized 시간 복잡도는 같은 자료구조에서 연이어서 연산을 했을 때의 평균 시간 복잡도로, 어떤 연산에서 $O(N)$이 걸리더라도 그 이후의 연산에서 계속 $O(1)$이 걸린다면 amortized 시간 복잡도는 더 낮아질 수 있습니다. 하지만 persistent한 자료구조에서는 $O(N)$이 걸리는 바로 그 연산을 반복적으로 수행할 수 있기 때문에, amortization이 더 이상 의미가 없습니다.
따라서 union by rank를 써야 하고, 이때 $O(\log N)$ 시간 복잡도의 persistent array 연산을 $O(\log N)$번 수행하므로 시간 복잡도는 $O(\log^2 N)$이 됩니다.
Persistent Conclusion
이 글에서는 서술하지 않았지만, 다음 자료구조도 똑같은 테크닉으로 구현할 수 있습니다. 한번 생각해 보세요!
- Persistent priority queue, 연산 당 $O(\log N)$
- Persistent segment tree with lazy propagation, 연산 당 $O(\log N)$
- Persistent sqrt decomposition, 연산 당 $O(\sqrt N)$
한편, $S$의 크기에 관계 없이 $O(\log N)$ 시간에 노드를 업데이트할 수 있으며, in-degree가 $O(1)$이라는 가정 하에 $O(1)$ 시간에도 노드를 업데이트할 수 있음이 알려져 있습니다. 관심 있으신 분은 다음 논문을 참조하세요: James R. Driscoll, Neil Sarnak, Daniel D. Sleator, Robert E. Tarjan, Making data structures persistent, Journal of Computer and System Sciences, Volume 38, Issue 1, 1989, Pages 86-124.