PQ Tree (Part 1)
Table Of Contents
Introduction
안녕하세요, Aeren입니다!
이번 글은 Codeforces Global Round 15에서 알게 된 PQ tree를 소개하는 첫 번째 글입니다.
어떤 finite set $U$와 $U$의 subset들의 집합 $C$가 주어졌을 때, $U$의 permutation $P$가 permissible하다는 것은, $S$의 각 원소 $T$에 대하여, $T$의 원소들이 $P$에서 연속적으로 나타나는 것을 의미합니다. PQ tree는 주어진 constraint $C$에 대하여 모든 permissible permutation들의 set을 효율적으로 관리하는 data structure입니다.
이번 글에서는 PQ tree의 구조와 construction algorithm에 대해 소개하고, 다음 글에서는 효율적인 linear time algorithm과 PQ tree를 활용한 consecutive ones property, interval graph, 그리고 graph planarity 검사를 소개하겠습니다.
이 글은 다음 글을 바탕으로 작성되었습니다.
Structure of a PQ Tree
고정된 finite set $U = \lbrace a _ 1, \cdots , a _ m \rbrace$가 주어졌을 때, PQ tree over $U$란, 각 leaf가 $U$의 원소로 label되어 있고, 각 internal (non-leaf) node가 P 또는 Q로 label되어 있는 ordered rooted tree를 의미합니다. 즉, 다음 operation들을 유한번 반복하여 얻어낼 수 있는 tree를 PQ tree라 합니다.
-
어떤 $a \in U$에 대해, $a$로 label된 leaf 하나로 이루어진 tree를 만듭니다.
-
PQ tree $T _ 1, \cdots T _ k$가 주어질 때, P로 label된 node에 $T _ 1, \cdots , T _ k$의 root들을 child로 붙여서 tree를 만듭니다. 이러한 P node는 앞으로 다음 figure와 같이 원으로 나타내겠습니다.

-
PQ tree $T _ 1, \cdots T _ k$가 주어질 때, Q로 label된 node에 $T _ 1, \cdots , T _ k$의 root들을 child로 붙여서 tree를 만듭니다. 이러한 Q node는 앞으로 다음 figure와 같이 직사각형으로 나타내겠습니다.

PQ tree는 ordered rooted tree이므로 dfs order가 유일합니다. 이 dfs order에서 나타나는 leaf들의 label들의 sequence를 주어진 PQ tree $T$의 frontier라고 정의하고, $FRONTIER(T)$라 표기하겠습니다. 다음은 frontier가 $ABCDEFGHIJK$인 PQ tree의 예시입니다.

두 PQ tree $T _ 1$과 $T _ 2$가 equivalent하다는 것은, $T _ 1$에 다음 operation들을 유한번 반복하여 $T _ 2$를 얻어낼 수 있는 것을 의미합니다.
- $T _ 1$의 P node 하나를 골라 child들의 순서를 임의로 바꿔줍니다.
- $T _ 1$의 Q node 하나를 골라 child들의 순서를 반대로 바꿔줍니다.
$T _ 1$과 $T _ 2$가 equivalent하다는 것을 $T _ 1 \equiv T _ 2$라 표기하겠습니다. 위의 equivalence가 equivalence relation임은 자명합니다. 다음은 바로 위의 PQ tree와 equivalent한 PQ tree의 예시입니다.
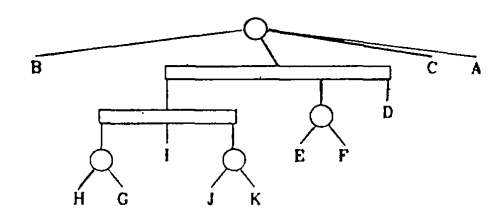
PQ tree $T$의 consistent frontier란 $T$와 equivalent한 PQ tree $T’$의 frontier를 의미합니다. 이러한 모든 consistent frontier들의 set을 $CONSISTENT(T)$라 정의하겠습니다.
$CONSISTENT(T) = \lbrace FRONTIER(T’): T \equiv T’ \rbrace$
어떤 PQ tree가 주어질때 우리는 이 consistent frontier가 조건을 만족하는 가능한 모든 permutation들의 집합을 나타내게 하고 싶습니다. 하지만 이에는 몇가지 문제가 있습니다. 첫번째로, frontier에 나타난 label들이 unique하지 않을 수 있습니다. 그리고 두번째로, child가 2개 이하인 P node와 Q node를 구분할 수 없어 representation이 unique하지 않습니다. 이를 해소하기 위해 어떤 PQ tree가 proper하다는 것을 다음 조건들을 만족하는 것으로 정의하겠습니다.
- 모든 $U$의 원소들은 정확히 한개의 leaf의 label입니다.
- 모든 P node들은 최소 두개의 child를 갖습니다.
- 모든 Q node들은 최소 세개의 child를 갖습니다.
우리의 목표는 permissible permutation들의 집합이 $CONSISTENT(T)$와 일치하는 proper PQ tree $T$를 얻어내는 것입니다.
Construction of a PQ Tree
먼저 특별한 PQ tree 두개를 소개하겠습니다.
-
Universal tree란 하나의 P node에 $U$의 모든 원소가 child로서 달려 있는 PQ tree입니다.
-
Null tree란 node가 하나도 없는 PQ tree입니다. 사실 node가 없으면 tree의 조건조차 만족하지 않지만, 논의의 편의성을 위해 이경우 특별히 허용하도록 하겠습니다.

Universal tree의 consistent frontier set은 $U$의 모든 permutation들을 포함합니다. 예를 들어 constraint $C$가 empty set일 경우 universal tree가 우리가 원하는 결과가 됩니다.
Null tree의 consistent frontier set은 empty set으로 정의합니다. $C$가 contradictory한 조건을 포함한다면 만족하는 permutation이 하나도 없으므로 null tree가 우리가 원하는 결과가 됩니다.
Operation Reduce
PQ tree는 정확히 하나의 연산을 지원합니다. PQ tree $T$와 $U$의 subset $S$가 주어졌을 때 $T$의 $S$-reduction은 $T$를 $CONSISTENT(T’)$가 $CONSISTENT(T)$에 포함되는 permutation중 $S$의 원소들이 인접하게 나타나는 permutation들의 집합이 되는 PQ tree $T’$으로 바꾸며 $REDUCE(T,S)$로 표기합니다. 그리고 constraint $C$에 대한 permissible permutation들의 집합을 consistent frontier set으로 갖는 PQ tree를 찾으려면 단순히 universal tree에서 시작하여 $C$의 각 원소 $S$에 대해 $T$가 null tree가 아닐 동안 $S$-reduction을 반복해 주면 됩니다.
어떤 node $u$의 subtree가 pertinent하다는 것은 $u$가 $u$의 subtree가 $S$를 포함하는 node중 깊이가 가장 작은 node라는 뜻이고, $PERTINENT(T,S)$라고 표기하겠습니다. 또한, 그러한 $u$를 $ROOT(T,S)$라 표기하겠습니다. 다음 figure는 처음 소개된 PQ tree $T$의 $S= \lbrace E,I,J,K \rbrace$에 대한 pertinent subtree입니다.
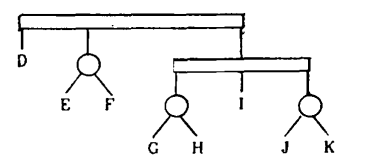
$S$-reduction은 $PERTINENT(T,S)$의 각 node를 깊이가 감소하는 순으로 방문하면서 각 node마다 template matching 이라는 과정을 거쳐저 진행됩니다. Template matching은 template과 replacement로 나눠져 있는데, 만약 어느 한 node에서 어떠한 template에도 matching되지 않는 상황이 발생했다면, 주어진 PQ tree는 즉시 null tree로 무너지고, 알고리즘은 종료됩니다.
각 node를 방문한 이후, 그 node에는 empty, full, partial중 하나의 label이 매겨지게 됩니다. Template-matching에서는 오직 현재 node의 상태와, child node들의 label에 관한 정보만 중요합니다. 특히, $ROOT(T,S)$의 label은 알고리즘에서 필요로 하지 않기에, 구지 언급하지 않겠습니다
Empty label은 현재 node의 subtree의 frontier가 $S$와 공통 원소를 갖지 않는단 뜻입니다.
Full label은 현재 node의 subtree의 frontier가 $S$의 subset이란 뜻입니다.
Partial label은 현재 node가 Q node이며, 어떤 consistent frontier $F$가 존재하여 $F$를 두 substring $L$과 $R$로 자를 수 있어, 둘 중 정확히 하나의 집합이 $S$의 subset이며, 정확히 하나의 집합이 disjoint함을 의미합니다
Leaf Node
일단 현재 node가 값 $x$를 나타내는 leaf node일 경우, $x$가 $S$의 원소라면 full, 아니라면 empty의 label을 붙인 후 다음 node로 넘어갑니다 (즉, replacement는 자기자신입니다).
P Node
현재 node $u$가 P node일 경우, 7가지 template이 존재합니다.
-
(Template P0 and P1) 만약 모든 child가 empty이거나, 혹은 모든 child가 full이면, $u$에는 각각 empty와 full의 label이 매겨지고 다음 노드로 넘어갑니다.
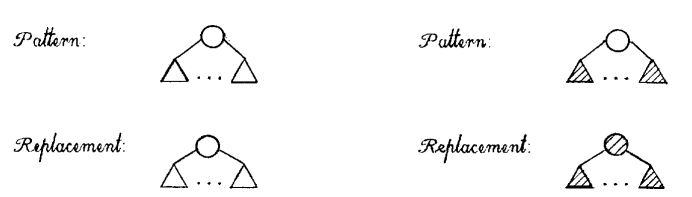
P0와 P1에 matching되지 않았지만, 모든 child가 empty 혹은 full일 경우, $u$가 $ROOT(T,S)$인지의 여부에 따라서 두 경우로 나뉩니다.
-
(Template P2) $u=ROOT(T,S)$인 경우, $u$의 모든 full child들을 묶어놓는 P node $v$가 $u$의 full child들과 교체됩니다. (단, 그러한 node가 한개라면, 아무일도 일어나지 않습니다.)

-
(Template P3) $u\ne ROOT(T,S)$일 경우, 모든 empty child를 묶어놓는 node $v$와 모든 full child를 묶어놓는 node $w$가 $u$의 두 child로 설정됩니다. (단, 각각의 label에 대해, 해당 child의 갯수가 1이면, 새로운 node는 추가되지 않습니다.) 이 때, $u$는 Q node로 바뀌며, partial로 label됩니다.


이제 한 개 이상의 partial child를 갖고 있는 경우를 보겠습니다.
Partial child가 한 개인 경우, 마찬가지로 root인지에 따라 경우가 나뉩니다.
-
(Template P4) $u=ROOT(T,S)$인 경우, $u$의 모든 full node들이 새로운 P node $v$로 옮겨 간 후, $v$가 $u$의 partial child의 full인 쪽 끝에 붙습니다. (단, full node가 한 개 이하이면, 그러한 $v$를 생성하지 않고 붙입니다.)
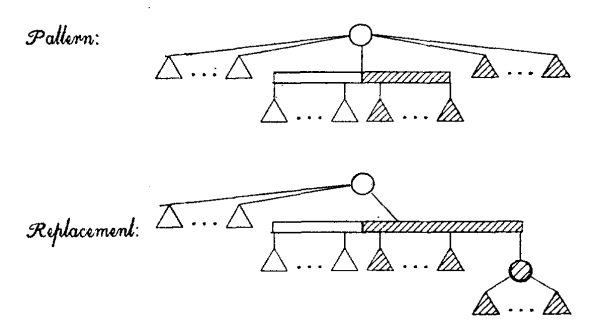
-
(Template P5) $u\ne ROOT(T,S)$인 경우, $u$의 partial child가 $u$로 대체된 후, 원래 $u$의 empty child를 묶어놓은 $v$와 full child를 묶어놓은 $w$가 각각 empty인 쪽 끝과 full인 쪽 끝에 붙습니다. (단, 각각 한 개 이하면, 그러한 node를 생성하지 않습니다.) 이 때, $u$는 Q node로 바뀌며, partial로 label됩니다.
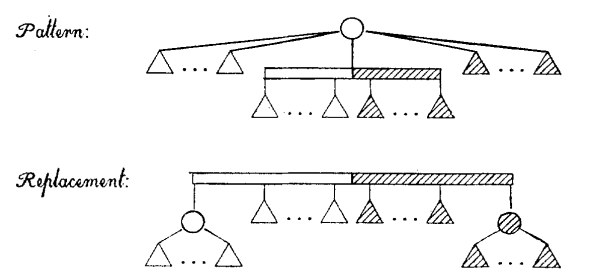
마지막으로, partial child가 두 개인 경우, 현재 node는 반드시 root여야 하며, 다음과 같은 형태로 matching됩니다.
-
(Template P6) 두개의 partial child들이 full child들을 묶는 새로운 node를 사이에 두고 full인 끝이 마주한 채로 합쳐집니다. (단, full node가 한 개 이하면, 그러한 node는 생성되지 않습니다.)
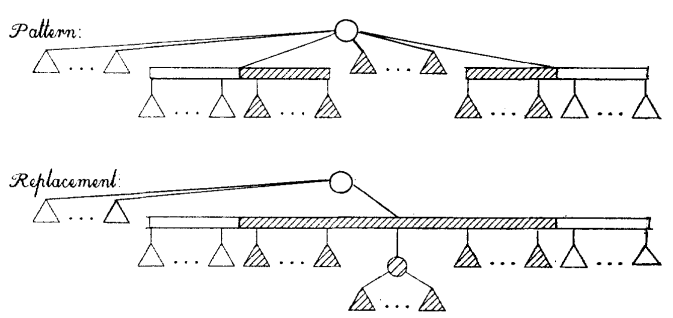
그리고 위의 template들에 모두 matching되지 않는다면, PQ tree는 null tree로 바뀌며 알고리즘이 종료됩니다.
Q Node
현재 node $u$가 Q node일 경우, 4가지 template이 존재합니다.
-
(Template Q0 and Q1) 만약 모든 child가 empty이거나, 혹은 모든 child가 full이면, $u$에는 각각 empty와 full의 label이 매겨지고 다음 노드로 넘어갑니다.
-
(Template Q2) 만약 partial child가 한 개이고, 그 partial child에 의해 $u$의 child가 empty와 full child로 분할된다면, partial child $v$의 모든 child들을 $v$대신 삽입 한 후, $v$를 삭제합니다. 이 때, $u$는 partial로 label됩니다.
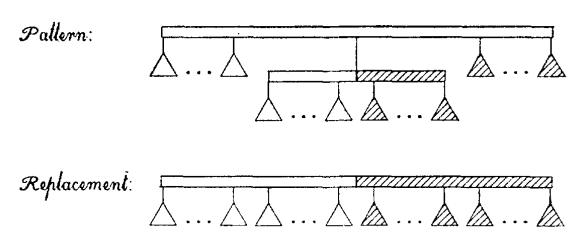
-
(Template Q3) 만약 partial child가 두 개이고, $u=ROOT(T,S)$이며, 그 partial child들에 의해 $u$의 child가 $L, M, R$ 세 부분으로 분할되고, $L$은 empty, $M$은 full, $R$은 empty node들로만 구성되어 있다면, Q2와 마찬가지로 partial child의 node들을 $u$에 삽입해 줍니다.
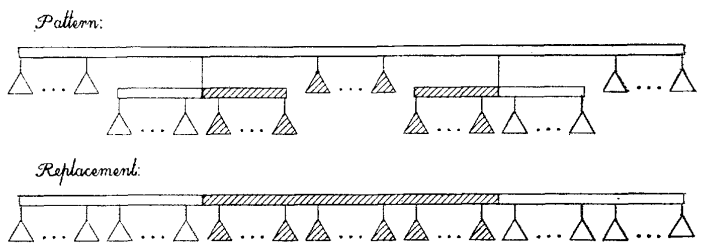
Implementation
다음은 위 알고리즘의 C++ 구현체입니다.
// Implmemtation of https://www.sciencedirect.com/science/article/pii/S0022000076800451
struct pq_tree{
int n;
bool is_null_tree = false;
vector<vector<int>> adj;
/*
For internal nodes, data indicates whether current node is P node(stores 0) or Q node(stores 1).
For leaf nodes, data represents the value
*/
vector<int> data;
pq_tree(int n): n(n), adj(n + 1), data(n + 1), label(n + 1), in_s(n){
adj[0].resize(n);
iota(adj[0].begin(), adj[0].end(), 1);
iota(data.begin() + 1, data.end(), 0);
}
operator bool(){
return !is_null_tree;
}
int new_node(int type, int state){
adj.emplace_back();
data.push_back(type);
label.push_back(state);
return (int)adj.size() - 1;
}
/*
Label
0: empty
1: full
2: partial
*/
vector<int> label, in_s;
// O(n^2)
bool reduce(const vector<int> &s){
if(is_null_tree) return false;
if((int)s.size() == 1) return true;
fill(in_s.begin(), in_s.end(), false);
for(auto x: s) in_s[x] = true;
bool done = false;
auto dfs = [&](auto self, int u)->int{
if(adj[u].empty()){
// Leaf node
return label[u] = in_s[data[u]];
}
int deg = (int)adj[u].size(), pertinence = 0;
array<int, 3> count{};
for(auto v: adj[u]){
pertinence += self(self, v);
if(is_null_tree || done) return 0;
++ count[label[v]];
}
bool is_root = pertinence == (int)s.size();
if(data[u] == 0){
// P node
if(count[0] == deg){
// Template P0
label[u] = 0;
}
else if(count[1] == deg){
// Template P1
label[u] = 1;
}
else if(count[0] + count[1] == deg){
if(is_root){
// Template P2
int u2 = new_node(0, 1);
auto it = partition(adj[u].begin(), adj[u].end(), [&](int v){ return label[v] == 0; });
move(it, adj[u].end(), back_inserter(adj[u2]));
adj[u].erase(it, adj[u].end());
adj[u].push_back(u2);
}
else{
// Template P3
array<int, 2> v;
for(auto t = 0; t < 2; ++ t){
if(count[t] == 1){
v[t] = *find_if(adj[u].begin(), adj[u].end(), [&](int v){ return label[v] == t; });
}
else{
v[t] = new_node(0, t);
auto it = partition(adj[u].begin(), adj[u].end(), [&](int v){ return label[v] != t; });
move(it, adj[u].end(), back_inserter(adj[v[t]]));
}
}
adj[u] = {v[0], v[1]};
data[u] = 1;
label[u] = 2;
}
}
else if(count[2] == 1){
if(is_root){
// Template P4
if(auto it = partition(adj[u].begin(), adj[u].end(), [&](int v){ return label[v] != 1; }); adj[u].end() - it >= 2){
int u2 = new_node(0, 1);
move(it, adj[u].end(), back_inserter(adj[u2]));
adj[u].erase(it, adj[u].end());
for(auto v: adj[u]){
if(label[v] == 2){
if(label[adj[v].back()] != 1) reverse(adj[v].begin(), adj[v].end());
adj[v].push_back(u2);
break;
}
}
}
else if(adj[u].end() - it == 1){
int u2 = adj[u].back();
adj[u].pop_back();
for(auto v: adj[u]){
if(label[v] == 2){
if(label[adj[v].back()] != 1) reverse(adj[v].begin(), adj[v].end());
adj[v].push_back(u2);
break;
}
}
}
if(count[0] == 0){
int v = adj[u][0];
adj[u] = adj[v];
adj[v].clear();
data[u] = 1;
label[u] = 2;
}
}
else{
// Template P5
array<int, 2> v{-1, -1};
for(auto t = 0; t < 2; ++ t){
if(count[t] == 1) v[t] = *find_if(adj[u].begin(), adj[u].end(), [&](int v){ return label[v] == t; });
else if(count[t] >= 2){
v[t] = new_node(0, t);
for(auto w: adj[u]) if(label[w] == t) adj[v[t]].push_back(w);
}
}
int pu = *find_if(adj[u].begin(), adj[u].end(), [&](int v){ return label[v] == 2; });
if(label[adj[pu][0]]) reverse(adj[pu].begin(), adj[pu].end());
adj[u].clear();
if(~v[0]) adj[u].push_back(v[0]);
move(adj[pu].begin(), adj[pu].end(), back_inserter(adj[u]));
if(~v[1]) adj[u].push_back(v[1]);
data[u] = 1;
label[u] = 2;
}
}
else if(count[2] == 2 && is_root){
// Template P6
int v = -1;
if(count[1] == 1){
auto it = find_if(adj[u].begin(), adj[u].end(), [&](int v){ return label[v] == 1; });
v = *it;
adj[u].erase(it);
}
else if(count[1] >= 2){
v = new_node(0, 1);
auto it = partition(adj[u].begin(), adj[u].end(), [&](int v){ return label[v] != 1; });
move(it, adj[u].end(), back_inserter(adj[v]));
adj[u].erase(it, adj[u].end());
}
array<int, 2> w;
auto it = find_if(adj[u].begin(), adj[u].end(), [&](int v){ return label[v] == 2; });
w[0] = *it;
it = find_if(next(it), adj[u].end(), [&](int v){ return label[v] == 2; });
w[1] = *it;
if(label[adj[w[0]][0]] != 0) reverse(adj[w[0]].begin(), adj[w[0]].end());
if(~v) adj[w[0]].push_back(v);
if(label[adj[w[1]][0]] != 1) reverse(adj[w[1]].begin(), adj[w[1]].end());
move(adj[w[1]].begin(), adj[w[1]].end(), back_inserter(adj[w[0]]));
adj[w[1]].clear();
adj[u].erase(it);
count[1] = 0;
if(count[1]) is_null_tree = true;
}
else is_null_tree = true;
}
else{
// Q node
if(count[0] == deg){
// Template Q0
label[u] = 0;
}
else if(count[1] == deg){
// Template Q1
label[u] = 1;
}
else{
if(label[adj[u].back()] == 0) reverse(adj[u].begin(), adj[u].end());
if(label[adj[u].front()] != 0 && label[adj[u].back()] == 2) reverse(adj[u].begin(), adj[u].end());
int i = 0;
while(label[adj[u][i]] == 0) ++ i;
int j = i + 1;
while(j < deg && label[adj[u][j]] == 1) ++ j;
if(j == deg){
// Template Q2
if(label[adj[u][i]] == 2){
int v = adj[u][i];
auto it = adj[u].erase(adj[u].begin() + i);
if(label[adj[v][0]] != 0) reverse(adj[v].begin(), adj[v].end());
adj[u].insert(it, adj[v].begin(), adj[v].end());
adj[v].clear();
}
label[u] = 2;
}
else{
int k = j + 1;
while(k < deg && label[adj[u][k]] == 0) ++ k;
if(k == deg && is_root){
// Template Q3
if(i < j && label[adj[u][j]] == 2){
int v = adj[u][j];
auto it = adj[u].erase(adj[u].begin() + j);
if(label[adj[v].front()] == 0) reverse(adj[v].begin(), adj[v].end());
adj[u].insert(it, adj[v].begin(), adj[v].end());
adj[v].clear();
}
if(label[adj[u][i]] == 2){
int v = adj[u][i];
auto it = adj[u].erase(adj[u].begin() + i);
if(label[adj[v].back()] == 0) reverse(adj[v].begin(), adj[v].end());
adj[u].insert(it, adj[v].begin(), adj[v].end());
adj[v].clear();
}
}
else is_null_tree = true;
}
}
}
if(is_root) done = true;
return pertinence;
};
dfs(dfs, 0);
return !is_null_tree;
}
template<class T>
T count_permutation() const{
if(is_null_tree) return 0;
vector<T> fact(n + 1, 1);
for(auto x = 1; x <= n; ++ x) fact[x] = fact[x - 1] * x;
auto dfs = [&](auto self, int u)->T{
T res = adj[u].empty() ? 1 : data[u] ? 2 : fact[(int)adj[u].size()];
for(auto v: adj[u]) res *= self(self, v);
return res;
};
return dfs(dfs, 0);
}
vector<int> frontier() const{
vector<int> order;
auto dfs = [&](auto self, int u)->void{
if(adj[u].empty()) order.push_back(data[u]);
for(auto v: adj[u]) self(self, v);
};
dfs(dfs, 0);
return order;
}
};